
第三章静电能 §3.1真空中点电荷间的相互作用能 §3.2连续电荷分布的静电能 §3.3电荷体系在外电场中的静电能 §3.4电场的能量和能量密度 *§3.5非线性介质及电滞损耗 *§3.6利用静电能求静电力
第三章 静电能 §3.1 真空中点电荷间的相互作用能 §3.2 连续电荷分布的静电能 §3.3 电荷体系在外电场中的静电能 §3.4 电场的能量和能量密度 *§3.5 非线性介质及电滞损耗 *§3.6 利用静电能求静电力

静电能的定义 建立一个带电系统的过程中,总伴随着 电荷相对运动,需要外力克服电荷间的相互 作用而作功。外力作功所消耗的能量将转换 为带电系统的能量,该能量定义为带电系统 的静电能。显然,静电能应由系统的电荷分 布决定。 例如,第一章中已讲到的点电荷在外电 场中的电势能就是静电能。这是静电场为保 守力场的必然结果
建立一个带电系统的过程中,总伴随着 电荷相对运动,需要外力克服电荷间的相互 作用而作功。外力作功所消耗的能量将转换 为带电系统的能量,该能量定义为带电系统 的静电能。显然,静电能应由系统的电荷分 布决定。 例如,第一章中已讲到的点电荷在外电 场中的电势能就是静电能。这是静电场为保 守力场的必然结果。 静电能的定义

能量的基本概念 引入的目的: 1. 能量是物质的共同属性,是物质运动的普遍量度; 2. 能量守恒定律是最有意义、最有用的发现之一; 3. 便于研究不同形式能量的转换。 二、 特点: 1. 是状态的单值函数, 属于整个系统; 2. 能量差才有意义; 3. 用做功来量度能量。 三、 描述的方法 按照其特点,要引入状态参量,规定零点能,然 后用做功来计算能量
能量的基本概念 一、引入的目的: 1. 能量是物质的共同属性,是物质运动的普遍量度; 2. 能量守恒定律是最有意义、最有用的发现之一; 3. 便于研究不同形式能量的转换。 二、特点: 1. 是状态的单值函数, 属于整个系统; 2. 能量差才有意义; 3. 用做功来量度能量。 三、描述的方法: 按照其特点,要引入状态参量,规定零点能,然 后用做功来计算能量

§3.1真空中点电荷间 的相互作用能 设想空间中有多个点电荷,其带电量用q 表示,初始时刻相互间距离为o, 相互作用 的库仑力为0。随后,外力克服库仑力做功, 使它们到达相应的位置”,任意两个点电 荷间的距离可以由rr=r给出。 ■ 这外力做功便转换成该点电荷系的能量,即 静电能 。 所谓点电荷之间的相互作用能,指的就是与 点电荷间的相对位置有关的静电能
§3.1 真空中点电荷间 的相互作用能 n 设想空间中有多个点电荷, 其带电量用 qi 表示, 初始时刻相互间距离为 ,相互作用 的库仑力为 0。随后,外力克服库仑力做功, 使它们到达相应的位置 ri , 任意两个点电 荷间的距离可以由 rij=|rij|=|rj-ri|给出。 n 这外力做功便转换成该点电荷系的能量,即 静电能。 n 所谓点电荷之间的相互作用能,指的就是与 点电荷间的相对位置有关的静电能

因此,状态参量取为r;(i,j=1,2,,N), 初始时刻1,→0,相互作用的库仑力为 零,它们之间的静电相互作用消失,很自 然地取这种状态的相互作用能为零。 下面,我们用一种类似于数学归纳法的办 法来计算由个点电荷组成的静电体系的 静电能
n 因此,状态参量取为rij(i, j = 1,2,…,N), 初始时刻 ,相互作用的库仑力为 零,它们之间的静电相互作用消失,很自 然地取这种状态的相互作用能为零。 n 下面,我们用一种类似于数学归纳法的办 法来计算由N 个点电荷组成的静电体系的 静电能

两个点电荷时 一个点电荷q在外电场U中的电势能W=qU 设电势U是由另一个点电荷Q产生的,于是点电 荷q具有的电势能可以写作 9Q W=qU= 4π£。 同样地,上式也表示了Q在q的电场中的电势能; 这电势能W即静电能,属于点电荷q与Q组成的 系统
两个点电荷时 n 一个点电荷q在外电场U中的电势能W=qU n 设电势U是由另一个点电荷Q产生的, 于是点电 荷q具有的电势能可以写作 ■ 同样地, 上式也表示了Q在q的电场中的电势能; 这电势能W即静电能,属于点电荷q与Q组成的 系统。 0 1 4 qQ W qU r

当两个点电荷分别为q1和q2时,静电能为: W12=92012= q291 4π8o1i2 同样地, W21=41U21= qq2=W2’ 4π8o12 可将两个点电荷的静电能记为W,,为方便写成: w,=a+形)=2(g,U+4 ■三个点电苻的静电能记为W3,便为: 形=2所++现,+形+形+2)
n 当两个点电荷分别为q1和q2时, 静电能为: 同样地, 可将两个点电荷的静电能记为W2 ,为方便写成: n 三个点电荷的静电能记为W3 ,便为: 2 1 12 2 12 0 12 1 , 4 q q W q U r 1 2 21 1 21 12 0 12 , 4 q q W q U W r 2 12 21 2 12 1 21 1 1 ( ) ( ), 2 2 W W W q U q U 3 12 21 13 31 23 32 1 ( ) 2 W W W W W W W

于是可写成: 历-。+形+形。+华1十以+形》 g+4些+q*9些+9坠+些 二 英中G, 2 i=1 4元80j1 j≠i j≠i aU代入W: W,=8π60 q91 i=l i=1
■ 于是可写成: ■ U 代入W : 3 3 3 0 1 1 1 , 8 j i i j j i ji q q W r 3 12 21 13 31 23 32 2 12 1 21 3 13 1 31 3 23 2 32 3 3 1 1 3 0 1 1 ( ) 2 1 ( ) 2 1 , , 2 1 4 其中 j i j i i i ji i j j i j ji W W W W W W W q U q U q U q U q U q U q r qU U U
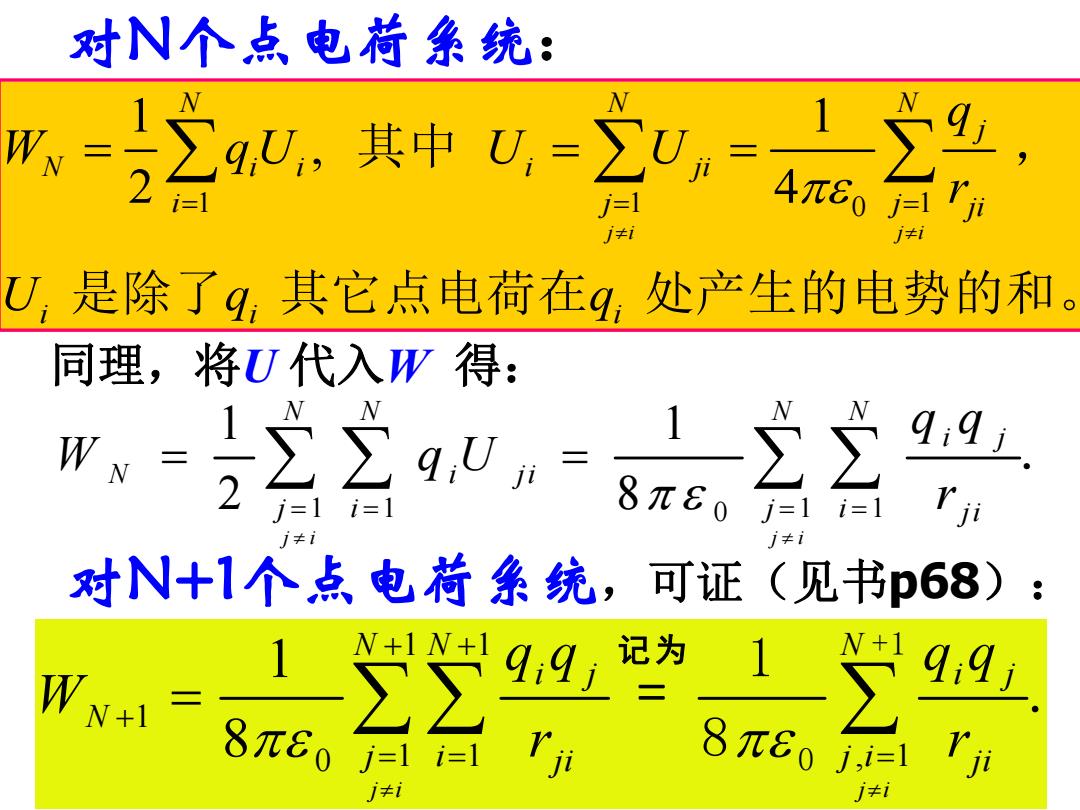
对N个点电苻象统: =Σ,其U-立,= i=1 j=1 4π80 j≠i j≠i U,是除了q,其它点电荷在q,处产生的电势的和。 同理,将U代入W得: WN- 991 2=1i j=1i=1 1≠i j≠i 对N+1个点电苻系统,可证(见书p68) W+1W+ Wx+= ∑∑ 记为 99j 8π0j=1 l i=1 8πeo j,i=1 j≠i j≠i
对N个点电荷系统: 1 1 0 1 1 1 , 2 4 其中 , 是除了 其它点电荷在 处产生的电势的和。 j i j i N N N j N i i i ji i j j ji i i i q W qU U U r U q q 同理,将U 代入W 得: 1 1 0 1 1 1 1 2 8 . j i j i N N N N i j N i ji j i j i ji q q W q U r 对N+1个点电荷系统,可证(见书p68): 1 1 1 0 1 1 , 1 1 8 j i j i N N N i j i j N j i j i ji ji q q q q W r r +1 0 1 . 8 = 记为

§3.2连续电荷分布的静电能 首先讨论空间只有自由电荷的情形,这 意味着电场空间中只允许导体和介电常量恒 等于o的物体(包括真空)存在。 1.先考虑体电荷分布的情况,电荷密 度设为P(r)。将该体电荷无限分割并把每一 小部分当作点电荷处理,则由前节结论可得: R.∬.(U,()dr, (3.2.1) U(r)表示除p(r)dV外其余所有电荷在r处 产生的电势
§3.2 连续电荷分布的静电能 首先讨论空间只有自由电荷的情形,这 意味着电场空间中只允许导体和介电常量恒 等于 的物体(包括真空)存在。 1. 先考虑体电荷分布的情况,电荷密 度设为 。将该体电荷无限分割并把每一 小部分当作点电荷处理,则由前节结论可得: 0 ( ) e r 1 1 ( ) ( ) , 2 e e V W U dV r r U1(r)表示除 外其余所有电荷在r处 产生的电势。 ( ) e r dV (3.2.1)