
例 导波理论 导波场的行波解 导波场的横向与纵向分量 导波场的传播参数 矩形波导中的电磁波 圆柱波导中的电磁波 同轴波导中的电磁波 导波场的正交性 波导中的能量与功率 波导损耗 波导的激励 介质波导 I
导波理论 导波场的正交性 导波场的行波解 波导中的能量与功率 波导损耗 波导的激励 介质波导 导波场的横向与纵向分量 矩形波导中的电磁波 圆柱波导中的电磁波 同轴波导中的电磁波 导波场的传播参数

导行电磁波一 被限制在某一特定区域内传播的电磁波 导波系统—一 引导电磁波从一处定向传输到另一处的装置 常用的导波系统的分类: TEM传输线、金属波导管、表面波导。 平行线 同轴波导 矩形波导 圆波导 微带线 K
导行电磁波 —— 被限制在某一特定区域内传播的电磁波 常用的导波系统的分类 : TEM传输线、金属波导管、表面波导。 导波系统 —— 引导电磁波从一处定向传输到另一处的装置 矩形波导 圆波导 微带线

7-1导波场的行波解 规则波导:沿轴线方向的几何形状、结构、参数都不变。 波动方程 (k2 =o'ue) 电磁波沿轴线(z轴)方向传播,设导波的电磁场矢量为 E)=E(4,42)Z(z)2H(r)=H(4,2)Z(2) e” (飞2+k2=k2) V=Vr+e: )Z()=0 dz te2 houz Z(z)=eti. 横向算符 K
1 2 1 2 E r E u u Z z H r H u u Z z ( ) ( , ) ( ), ( ) ( , ) ( ) = = 电磁波沿轴线(z 轴)方向传播,设导波的电磁场矢量为 7-1 导波场的行波解 1 2 1 1 2 2 T e e h u h u = + —— 横向算符 规则波导:沿轴线方向的几何形状、结构、参数都不变。 则由 2 2 2 ( ) c z k k k + = 2 2 ( ) k = 2 2 ( ) 0 E k H + = 波动方程 2 2 1 2 1 2 ( , ) ( ) 0 ( , ) T c E u u k H u u + = 2 d 2 ( ) ( ) 0 d z k Z z z + = T z e z = + 2 2 ( ) 0 E k H + = ( ) e z jk z Z z =

7-2导波场的横向与纵向分量 7-2-1 由纵向分量求横向分量 E(4,42)=E(4,42)+e.E.(4,42) Ei,一 横向分量 H(4,4)=H(4,4)+eH.(4,42) E、H一纵向分量 由V×E=(V,-ejk)x(E,+eE)=Vn×En-jke×E,+V,x(e.E) =-joM(Hr+e.H.) V×E=-joH →Vr×E,=-e.jwuH jke.×E,+e.×V,E.=jouH7 同理 V,×H=e.jocE jke×H,+e.×V,H.=-josE, 店,-Uex,A-,E] H,--joe×v,E-,H
7-2-1 由纵向分量求横向分量 1 2 1 2 1 2 ( , ) ( , ) ( , ) E u u E u u e E u u = + T z z 1 2 1 2 1 2 ( , ) ( , ) ( , ) H u u H u u e H u u = + T z z ( ) = − + E e jk E e E ( ) ( ) T z z T z z = − + T T z z T T z z E jk e E e E ( ) T z z = − + j H e H ET 、 HT— 横向分量 E z 、 H z— 纵向分量 = − T T z z E e j H z z T z T z T jk e E e E j H + = 由 = T T z z H e j E z z T z T z T 同理 jk e H e H j E + = − 2 1 [ ] T z T z z T z c E j e H jk E k = − 2 1 [ ] T z T z z T z c H j e E jk H k = − − = − E j H 7-2 导波场的横向与纵向分量

7-2-2E,与H的关系 (1)TE波(E=0) c5=v,点=,一店-ei=iE ou 一TE波的波阻抗 k (2)TM波(H.=0) hE+eg月=-a一月=袋eE=E TM TM波的波阻抗 os
TE — TE波的波阻抗 z Z k = TM z — TM波的波阻抗 k Z = 7-2-2 ET 与 HT 的关系 z z T z T z T jk e H e H j E + = − z z T z T z T jk e E e E j H + = (1)TE波( E z = 0 ) T z T T z TE z j E e H Z H e jk = − = (2)TM波( H z = 0 ) TM 1 T z T z T z j H e E e E jk Z = =

小结 例 [乐=exp,-v,E】 1 li--joee.xV,E.-jk.V,H.] k2 E jo4e.×VrH: Er =ZTEHr xe TE波 H jk:V H. ⊙u k jk:VE TM波 H= H,=- ote.xV:E. 0
2 1 [ ] T z T z z T z c H j e E jk H k = − − 2 1 [ ] T z T z z T z c E j e H jk E k = − TE波 T z T z 2 c j E e H k = 2 z T T z c jk H H k = − TM波 2 z T T z c jk E E k = − T z T z 2 c j H e E k = − 小结 TE z Z k = E Z H e T T z = TE TM z k Z = TM 1 H e E T z T Z =

7-3导波场的传播参数 方程:(V?+k2)w(4,2)=0 V-E.,H. 边界条件:uw+a兴1:=0 a1=0一TE波 O2=0一TM波 本征值问题:k。一本征值 业一本征函数 传播特性由k和k。确定: kk2k.=-j0一衰减; 截止参数: 2元 k。一截止波数;元。= Ke :藏止诚长人-元一薇上斑车
方程: 本征值问题: 2 2 2 c z k k k = + 传播特性由k 和kc确定: 2 2 1 2 ( ) ( , ) 0 T c + = k u u 边界条件: 1 2 ( ) 0 S n + = c k — 本征值 — 本征函数 , E H z z 1 = 0— TE波 2 = 0— TM波 2 2 2 z c k k k = − 2 2 c k k 2 2 c k k = 2 2 c k k c k — 截止波数; 1 c c f = — 截止频率 z k = — 传播; 0 z k = — 振荡; z k j = − — 衰减; 2π c c k = — 截止波长; 截止参数: 7-3 导波场的传播参数

传播参数 相位常数 B=k2-k2 =kv1-(kg/k) =kV1-(f/f)2=kV1-(1)2 2元 2元 2元 导波波长 ABk-(1) > k 0 相速 ,5Bk-f.1f) 群速 -0厅分 do I
导波波长 g 2 c 2π 2π 2π k f f 1 ( / ) k = = − 相位常数 p 2 c 1 ( / ) v k f f k = = − 相速 2 2 2 c 2 2 c c 1 ( / ) 1 ( / ) 1 ( / ) c k k k k k k f f k = − = − = − = − 传播参数 2 g c d 1 ( / ) d v f f k k 群速 = = −

波阻抗 →Kp→Z= j08 08 -n层 au jk. k>k2→k=-ja→Z=, (电容性) J08 J04 (电感性) k=k2→k=0→ZM=0(串联谐振);ZE=o(并联谐振) 传播条件 工作频率f高于截止频率f、的才能在波导中传播 K
TE 2 c z 1 ( ) j Z jk k f f = = = − 工作频率 f 高于截止频率fc的才能在波导中传 播 传播条件 波阻抗 2 2 c k k 2 2 c k k z k = 0 z k = c k j = − 2 TM c 1 ( ) z jk k Z f f j = = = − TE j Z = TM j Z = (电容性) (电感性) 2 2 c k k = TM Z = 0 (串联谐振); ZTE = (并联谐振)
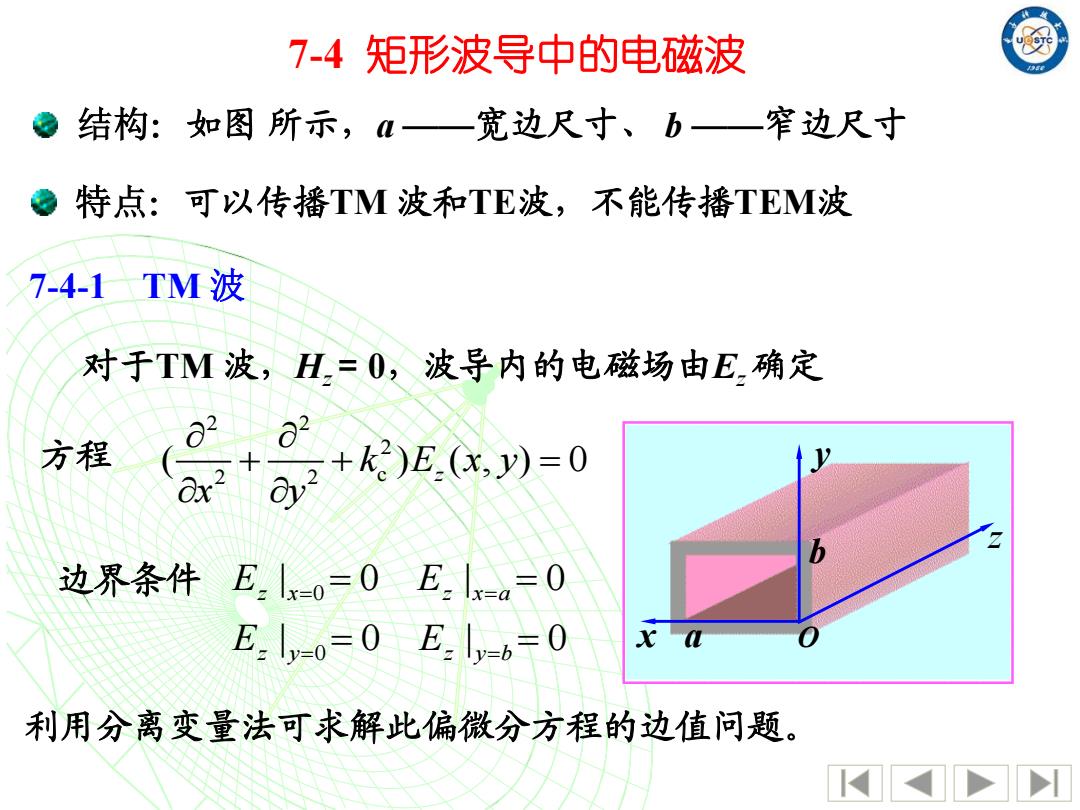
7-4矩形波导中的电磁波 结构:如图所示,一宽边尺寸、b—窄边尺寸 ©特点:可以传播TM波和TE波,不能传播TEM波 7-4-1TM波 对于TM波,H,=0,波导内的电磁场由E确定 ∂2 方程 )E.(.)=0 边界条件E.1xo=0E.lx-a=0 E:ly-0=0 E ly-6=0 x a 利用分离变量法可求解此偏微分方程的边值问题
7-4 矩形波导中的电磁波 对于TM 波,Hz = 0,波导内的电磁场由Ez 确定 边界条件 | 0 | 0 | 0 | 0 0 0 = = = = = = = = z y z y b z x z x a E E E E x y z O b a 7-4-1 TM 波 2 2 2 2 2 c ( ) ( , ) 0 z k E x y x y + + = 方程 结构:如图 所示,a ——宽边尺寸、 b ——窄边尺寸 特点:可以传播TM 波和TE波,不能传播TEM波 利用分离变量法可求解此偏微分方程的边值问题