第4章: 重要定理和原理 古等电嫩场理论 4.1 惟一性定理 4.2 镜像原理 4.3 互易定理 4.4 等效原理 4.5互补原理 K
第 4 章 重要定理和原理 高等电磁场理论 4.1 惟一性定理 4.2 镜像原理 4.3 互易定理 4.4 等效原理 4.5 互补原理

第4章 重要定理和原理 古普电赋场理论 §4.1电磁场惟一性定理 条件:(1)已知区域内源分布; (2)已知初始时刻区域内的场分布; (3)已知边界面上的n×E或n×H。 结论:区域V内的电磁场分布是惟一的。 n 或 E,月 V
第 4 章 重要定理和原理 高等电磁场理论 §4.1 电磁场惟一性定理 V m J J S n E H, n H n E 或 条件: (2)已知初始时刻区域内的场分布; (3)已知边界面上的 n E 或 n H 。 (1)已知区域内源分布; 结论:区域V 内的电磁场分布是惟一的
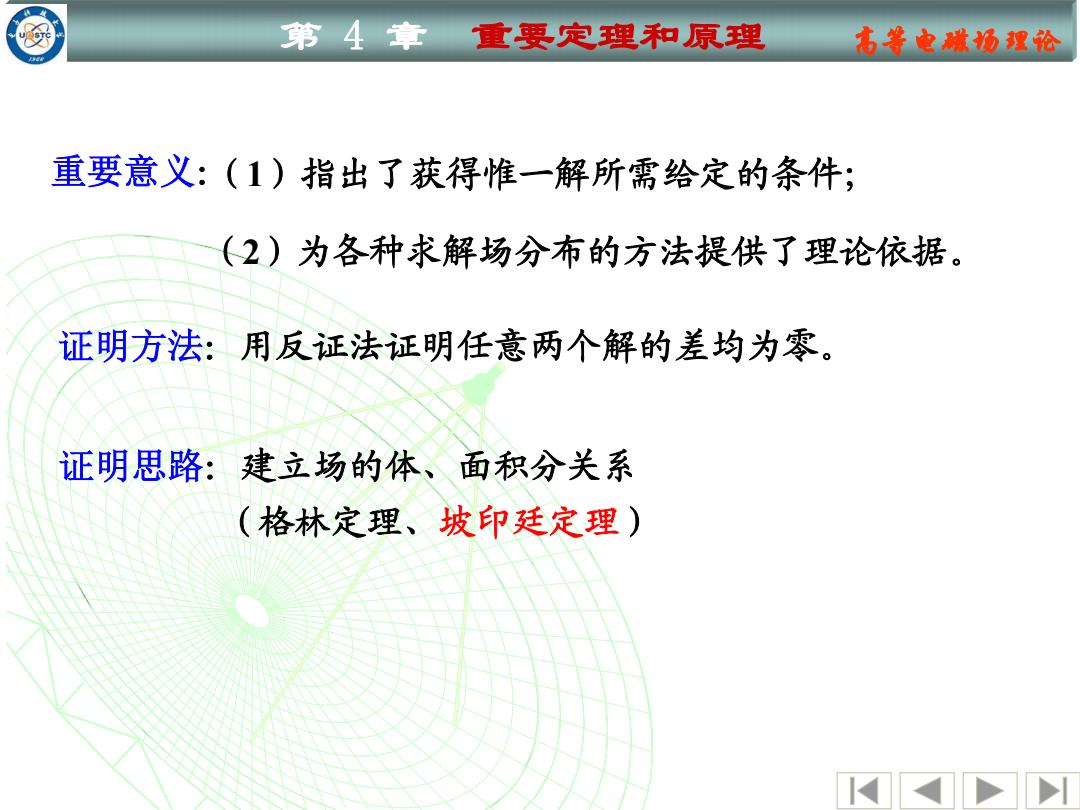
例 第4章: 重要定理和原理 右普电赋场理论 重要意义:(1)指出了获得惟一解所需给定的条件; (2)为各种求解场分布的方法提供了理论依据。 证明方法:用反证法证明任意两个解的差均为零。 证明思路:建立场的体、面积分关系 (格林定理、坡印廷定理)
第 4 章 重要定理和原理 高等电磁场理论 重要意义: (2)为各种求解场分布的方法提供了理论依据。 (1)指出了获得惟一解所需给定的条件; 证明思路:建立场的体、面积分关系 (格林定理、坡印廷定理) 证明方法:用反证法证明任意两个解的差均为零

第4章 重要定理和原理 右等电微场理论 证明:假设有两组解:EDH、B,;E2、D2H2B, 则x,=7,6股.vx4-- 8t V·B2=pm,7.D2=p 令E。=E-E,、D,=D,-D、i=i,-H2B。=B-B, 则 VxH-E+0pVx-08 v.B-0 v.D-0 8t 且 ixHols=nx Hs-nx Has=0 nx Eols=nxEls-nxE2s=0 Fol-o=F1l-o-E2l0=0 Hol-o=H1-0-H2-0=0
第 4 章 重要定理和原理 高等电磁场理论 证明: 1,2 1,2 m 1,2 1,2 , D B H J E J t t = + = − − m 1,2 1,2 = = B D , 令 E E E D D D H H H B B B 0 1 2 0 1 2 0 1 2 0 1 2 = − = − = − = − 、 、 、 0 0 0 0 0 0 0 0 0 D B H E E B D t t = + = − = = , , , 且 0 1 2 0 S S S n H n H n H = − = 0 1 2 0 S S S n E n E n E = − = 0 0 1 0 2 0 0 E E E 0 0 1 0 2 0 t t t = = = = − = 0 , H H H t t t = = = = − = 1 1 1 1 2 2 2 2 假设有两组解: E D H B E D H B 、 、 、 ; 、 、 、 则 则

第4章: 重要定理和原理 古等电嫩场理论 由坡印廷定理,在区域V上,有 医+8er+fa业-手i)s =-∮,(i×E)·HdS=-∮,(H×nm)EdS=0 a0r=rs0 对于线性、各向同性的媒质 写g+号ar-医09r0 ~F+ar=0→气时+号Ha业s0>0) → g+号H=0→E=H=0→E=E,i,=A, 2 2
第 4 章 重要定理和原理 高等电磁场理论 由坡印廷定理,在区域V上,有 2 0 0 0 0 0 0 0 ( )d d ( ) d V V S D B E H V E V E H n S t t + + = − 0 0 0 0 ( ) d ( ) d 0 S S = − = − = n E H S H n E S 2 2 0 0 0 2 2 E H + = 0 0 E H= = 0 1 2 1 2 E E H H = = , 2 2 0 0 0 ( ) d 0 2 2 t V E H V + = = 2 2 0 0 ( )d 0 ( 0) 2 2 V E H V t + 2 0 0 0 0 0 )d d 0 V V D B E H V E V t t + = − 2 2 0 0 0 0 0 0 d ( )d ( )d 0 d 2 2 V V D B E H V E H V t t t + = + 对于线性、各向同性的媒质
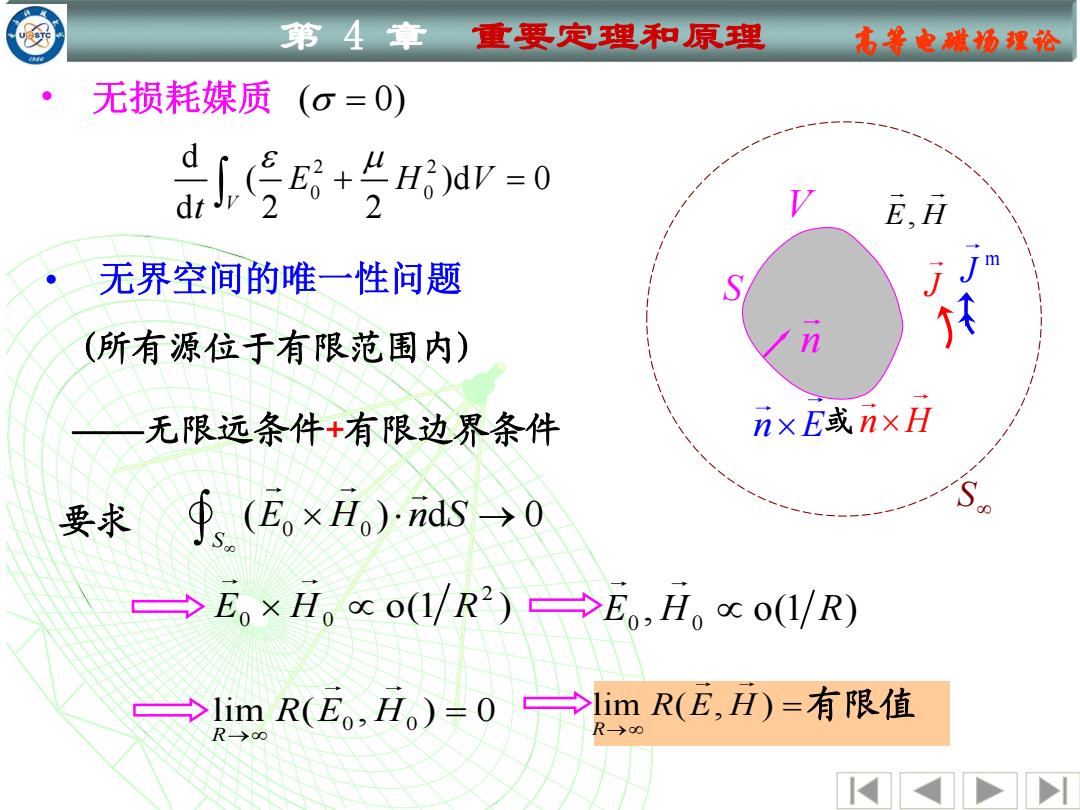
第4章 重要定理和原理 右等电嫩汤理论 无损耗媒质 (0=0) dav-o 2 E,H m 无界空间的唯一性问题 J (所有源位于有限范围内) 无限远条件+有限边界条件 nxE或nxH 要求 ∮、(E。×io)nds→0 →E。×H。co(1/R2)→Eo,H。∝o(1/R) →limR(Eo,Ho)=0→limR(E,H)=有限值 R>o∞
第 4 章 重要定理和原理 高等电磁场理论 • 无界空间的唯一性问题 (所有源位于有限范围内) 2 0 0 E H R o(1 ) 0 0 E H R , o(1 ) 0 0 lim ( , ) 0 R R E H → = 要求 0 0 ( ) d 0 S E H n S → ——无限远条件+有限边界条件 V m J S J n E H, n E 或 n H • 无损耗媒质 ( 0) = 2 2 0 0 d ( )d 0 d 2 2 V E H V t + = lim ( , ) R R E H → = 有限值 S

第4章; 重要定理和原理 古等电嫩场理论 时谐场的惟一性问题 无限的周期性取代了有限时刻的初始条件,没有初始条件。 ∮,(E×H)ids=jo(H·B-E,·D)dV+∫E。Jd" 线性、各向同性的媒质中D。=(e'-jeE B。=(h'-j")H。 →-④,(E×H)ndS=jo[W'j")H。H-(e'+je")E。·E]dV +∫GE.EdV →Ref区=o兮H+写兵r-jr →E,-E2=E。=0,H1-H2=H。=0
第 4 章 重要定理和原理 高等电磁场理论 无限的周期性取代了有限时刻的初始条件,没有初始条件。 1 2 0 1 2 0 E E E H H H − = = − = = 0, 0 0 0 0 0 0 0 0 0 ( ) d [( ) ( ) ]d d S V V E H n S j j H H j E E V E E V − = − − + + 0 0 0 0 0 0 0 0 ( ) d ( )d d S V V E H n S j H B E D V E J V − = − + 0 0 D j E = − ( ) 0 0 B j H = − ( ) 线性、各向同性的媒质中 0 0 0 0 0 0 0 0 1 Re ( ) d ( )d d 2 2 2 2 S V V E H n S H H E E V E E V − = + + 时谐场的惟一性问题
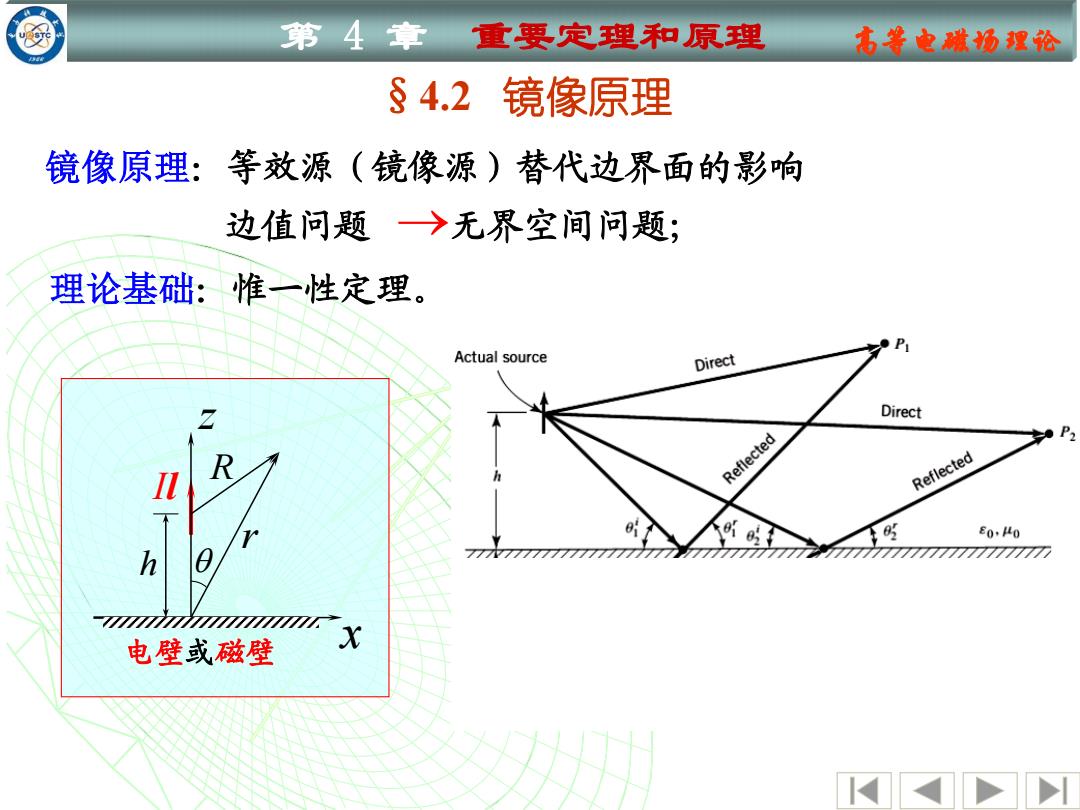
第4章 重要定理和原理 古普电赋场理论 §4.2镜像原理 镜像原理:等效源(镜像源)替代边界面的影响 边值问题→无界空间问题; 理论基础:惟一性定理。 P Actual source Direct Direct R Reflected Reflected 入 E0,0 777727777777777777777777777 电壁或磁壁
第 4 章 重要定理和原理 高等电磁场理论 §4.2 镜像原理 → 镜像原理:等效源(镜像源)替代边界面的影响 边值问题 无界空间问题; 理论基础:惟一性定理。 h R Il r z 电壁或磁壁 x
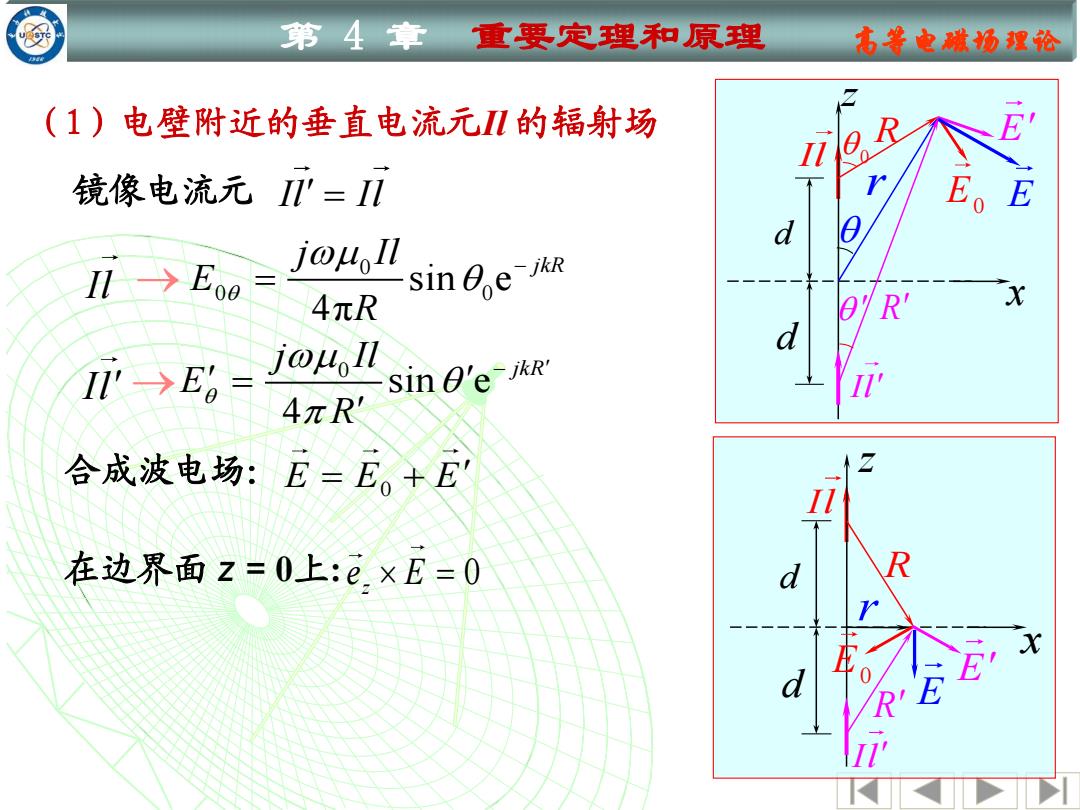
第4章 重要定理和原理 古等电嫩场理论 (1)电壁附近的垂直电流元IⅡ的辐射场 R 镜像电流元'=I几 Eo E Il→Eo6 joo d sin eR 4πR R X II'→E0= jool sin g'e-jR' 4πR' 合成波电场:E=E。+E 在边界面z=0上:e.×E=0 d R 0 d 三
第 4 章 重要定理和原理 高等电磁场理论 镜像电流元 Il Il = Il 0 0 0 sin e 4π jkR j Il E R − → = Il → 0 sin e 4 jkR j Il E R − = Il d r R E E0 E d R Il z x Il d r R E E E0 d R Il z x 0 E E E 0 = + 在边界面 z = 0上: 0 z e E = 合成波电场: (1)电壁附近的垂直电流元Il 的辐射场

例 第4章: 重要定理和原理 古等电嫩场理论 对于远区场:0,≈0'≈0,1/R≈1/R'≈1/r kR≈r-kd cos,kR'≈r+kd cos →Eg≈ u,"sin6e产eam,Eg六jo,sin0eeas0 4元r 4元r →Eg=Eo0+E0= j04I1 sine cos(kd cos)e 2πr ZA R R 0=∞
第 4 章 重要定理和原理 高等电磁场理论 0 , 1 1 1 R R r kR kr kd kR kr kd − + cos , cos x 0 0 cos cos 0 sin e e , sin e e 4π 4π jkr jkd jkr jkd j Il j Il E E r r − − − 对于远区场: 0 0 sin cos( cos )e 2π jkr j I l E E E kd r − = + = d d x y z Il Il R R r