
例 第一章 基本电磁理论 高等电赋场理论 讲授内容 麦克斯韦方程组 媒质的电磁特性一本构关系 边界条件 电磁能量与能流 波动方程 电磁位函数
第一章 基本电磁理论 高等电磁场理论 麦克斯韦方程组 媒质的电磁特性——本构关系 边界条件 电磁能量与能流 波动方程 电磁位函数 讲授内容

第一章」 基本电磁理论 高等电赋场理论 §1.1麦克斯韦方程组 1.1.1 时域麦克斯韦方程组(静止媒质) 1、微分形式 VxB=4,d+V×M+8oat Ot V×i=j+ aD at V×E= aB V×E= aB Ot Ot ☑.B=0 D=8E+P V.B=0 V.E=(p+pp)/80 H=B/Lo-M V.D=p
第一章 基本电磁理论 高等电磁场理论 § 1.1 麦克斯韦方程组 0 D H J t B E t B D = + = − = = 1.1.1 时域麦克斯韦方程组(静止媒质) 1、 微分形式 0 0 0 ( ) 0 ( ) / P E P B J M t t B E t B E = + + + = − = = + 0 0 / D E P H B M = + = −

第一章」 基本电磁理论 高等电赋场理论 ·Maxwell方程的独立性 V×i-j+D …(1) t 两个旋度方程是 aB V×E=- .…(2) 完全独立的;两 at 个散度方程不是 ☑B=0…(3) 完全独立的。 7D=p……(4) 7-j+2=0-…(5) 8t (1)、(5)→(4) (2)→(3)
第一章 基本电磁理论 高等电磁场理论 (1) (2) 0 (3) (4) D H J t B E t B D = + = − = = • (1)、(5)→(4) • (2)→(3) • Maxwell 方程的独立性 J 0 (5) t + = 两个旋度方程是 完全独立的;两 个散度方程不是 完全独立的
第一章」 基本电磁理论 高等电赋场理论 深刻揭示了电磁场的任意空间变化会转化成时间变化,反 过来,时间变化也会转化成空间变化。正是这种空间和时间的 相互转化构成了波动的外在形式。 T,时刻 T2时刻 Z 电磁波传播
第一章 基本电磁理论 高等电磁场理论 深刻揭示了电磁场的任意空间变化会转化成时间变化,反 过来,时间变化也会转化成空间变化。正是这种空间和时间的 相互转化构成了波动的外在形式。 电磁波传播

第一章 基本电磁理论 名等电喊场理论 ★FDTD方程的建立 OE E=eE,() Hy Ex V×H=8 8t H=e,H(=) -8 8z Ot aH OE. Hy V×E=-4 =u 8t 8z 8t (t) 6E oH, n E n+1 -8 0z 8t 0z Ot 1 (E,)H, n+ -2 n-1/2 n (H)Ex (H,)E uAz △t (E)H n 2 H,2-H,gE,2-Eg2 n-1 EAz △t i-1 i-1/2i i+1/2i+1(z)
第一章 基本电磁理论 高等电磁场理论 E H t H E t = = − ★ FDTD 方程的建立 y x x y H E z t E H z t = − = ( ) ( ) x x y y E e E z H e H z = = , n n x y i i E H z t = 1/2 1/2 1/2 1/2 n n n n x i x i y i y i i E E H H z t + − + − − − = n n y x i i H E z t = − i − 1 i − 1 / 2 i i + 1 / 2 i +1 n n −1 1 2 n − 1 2 n + n + 1 ( )t ( )z E x E x H y H y ( ) E x ( ) E x ( ) H y ( ) H y ? 1/2 1/2 1/2 1/2 n n n n y i y i x i x i i H H E E z t + − + − − − = −
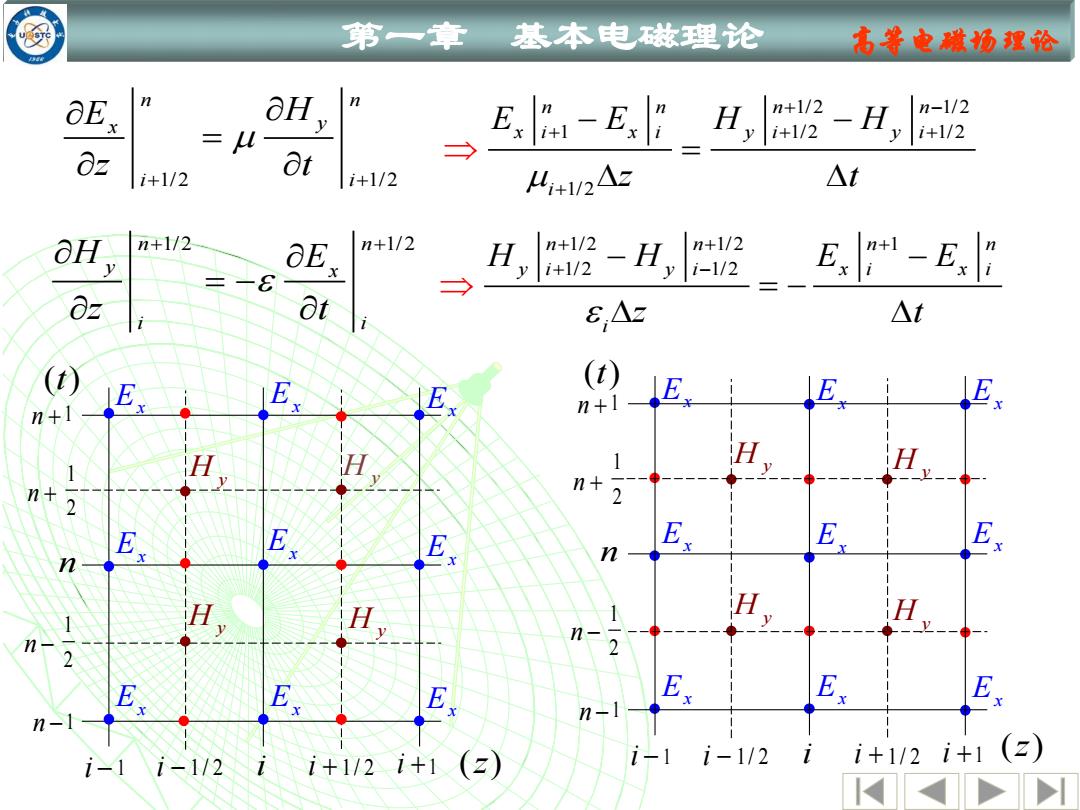
第一章 基本电磁理论 名等电喊场理论 aE. aH n 2 =4 E-E2_H,|m设-H, 8z i+1/2 8t i+1/2 4+1V2A正 △t aH n+1/2 E n+1/2 H,-H, n+1/2 i+1/2 i-1/2 Ex1-E日 82 i at 8,Az △t (t) n+1 E; E Ex (t) n+1 E 11 H H n+ n+ 2 2 E E E H. H n 2 E E E Ex E E n- n-1 (z) i-1i-1/2i i+112i+1(z) i-1i-1/2i i+1/2i+1
第一章 基本电磁理论 高等电磁场理论 1/2 1/2 n n x y i i E H z t + + = 1/2 1/2 1 1/2 1/2 1/2 n n n n x i x i y i y i i E E H H z t + − + + + + − − = 1/2 1/2 1 1/2 1/2 n n n n y i y i x i x i i H H E E z t + + + + − − − = − n n 1/2 1/2 y x i i H E z t + + = − E x H y H y E x E x E x E x E x E x i − 1 i − 1 / 2 i i + 1 / 2 i +1 n n −1 1 2 n − 1 2 n + n + 1 ( )t ( )z E x E x H y H y ( )t i − 1 i − 1 / 2 i i + 1 / 2 i +1 n n −1 1 2 n − 1 2 n + n + 1 ( )z E x E x H y H y E x H y H y E x E x E x E x E x E x

第一章」 基本电做理论 高等电赋场望论 2、积分形式 f. xFas w-15 f,- ∮nB-ds=0 ∮,B.ds=0 ∮,Dds=Spdr ∮.D.ds=jpdy 手ds=0r jus S S
第一章 基本电磁理论 高等电磁场理论 d ( ) d d d d 0 d d C S C S S S V D H l J S t B E l S t B S D S V = + = − = = 2、 积分形式 d d S V J S V t = − d ( )d d d d 0 d d S V S V S S V D n H S J V t B n E S V t B S D S V = + = − = = d d S V J S V t = − C S S V n

例 第一章」 基本电做理论 高等电赋场理论 1.1.2 频域麦克斯韦方程组(复数形式) 时谐场:单一频率变化的周期性稳态场。 用复夫量表示 E(r,t)=Re[E ()e] En(F)=eExm()+e,Evnm(P)+eEm(F)— 复矢量 E(G,)二一对应En(G) 麦克斯韦方程组的复数形式 V×H=j+j06 →j) V×E=-j0B 7.B=0 V.D=p
第一章 基本电磁理论 高等电磁场理论 1.1.2 频域麦克斯韦方程组 (复数形式) • 时谐场:单一频率变化的周期性稳态场。 • 麦克斯韦方程组的复数形式: 0 H J j D E j B B D = + = − = = m m m m ( ) ( ) ( ) ( ) E r e E r e E r e E r = + + x x y y z z m ( , ) Re[ ( )e ] j t E r t E r = —— 复矢量 用复矢量表示 ( ) j t → E r t ( , ) m E r( ) 一一对应

第一章」 基本电磁理论 高等电赋场理论 1.1.3 麦克斯韦方程组的广义形式、对偶原理 VxH=J+OD …(1) 8t V×E = aB (2) 8t V·B=0 。。。 (3) V·D=p …(4) 磁流与磁荷???
第一章 基本电磁理论 高等电磁场理论 1.1.3 麦克斯韦方程组的广义形式、对偶原理 (1) (2) 0 (3) (4) D H J t B E t B D = + = − = = 磁流与磁荷 ???

第一章」 基本电做理论 高等电赋场理论 1、磁流与磁荷 磁流、磁荷一人为引入的假想源(等效源) ■如:介质磁化→引入等效磁荷: p"=-4V·M、p=-4n·M m S S V.B=0 V.Bm =em M m B=4,(H+M) Bm=oH VxE=- aB aM 0Bm =-Jm aBm 8t =-0 Ot Ot m OM 其中jm=4,at (4V·M) 为等效磁流 且vm=g Ot 8t
第一章 基本电磁理论 高等电磁场理论 1、磁流与磁荷 磁流、磁荷——人为引入的假想源(等效源) m m = − = − 0 0 M n M 、 S 如:介质磁化 →引入等效磁荷: m m m 0 B M B B E J t t t t = − = − − = − − m m 0 ( ) M J t t = = − 其中 J m 0 M 为等效磁流 且 t = = B 0 M V S 0 B H M = + ( ) m m = B m V m S S m B H = 0