电子科技大学：《高等电磁场理论 Advanced Electromagnetic Field Theory》课程教学资源（课件讲稿）第五章 电磁辐射

第五章 电磁辐射 名等电赋场理论 电磁辐射场的求解 辐射场与辐射矢量 口径辐射场 分层媒质中的偶极子场 I

第五章 电磁辐射 高等电磁场理论 电磁辐射场的求解 辐射场与辐射矢量 口径辐射场 分层媒质中的偶极子场

第五章 电磁辐射 名等电赋场理论 传播问题：无源问题 辐射问题：有源问题一求已知的源分布在空间产生的辐射场 方法：求解有源矢量波动方程 V×7×i-k2i=-jo8jm+V×j V×V×E-k2E=-j0uJ-V×Jm

第五章 电磁辐射 高等电磁场理论 传播问题：无源问题 2 m     − = − +   H k H j J J   2 m     − = − −   E k E j J J  x y z o r r  R m J J P 方法：求解有源矢量波动方程 辐射问题：有源问题——求已知的源分布在空间产生的辐射场

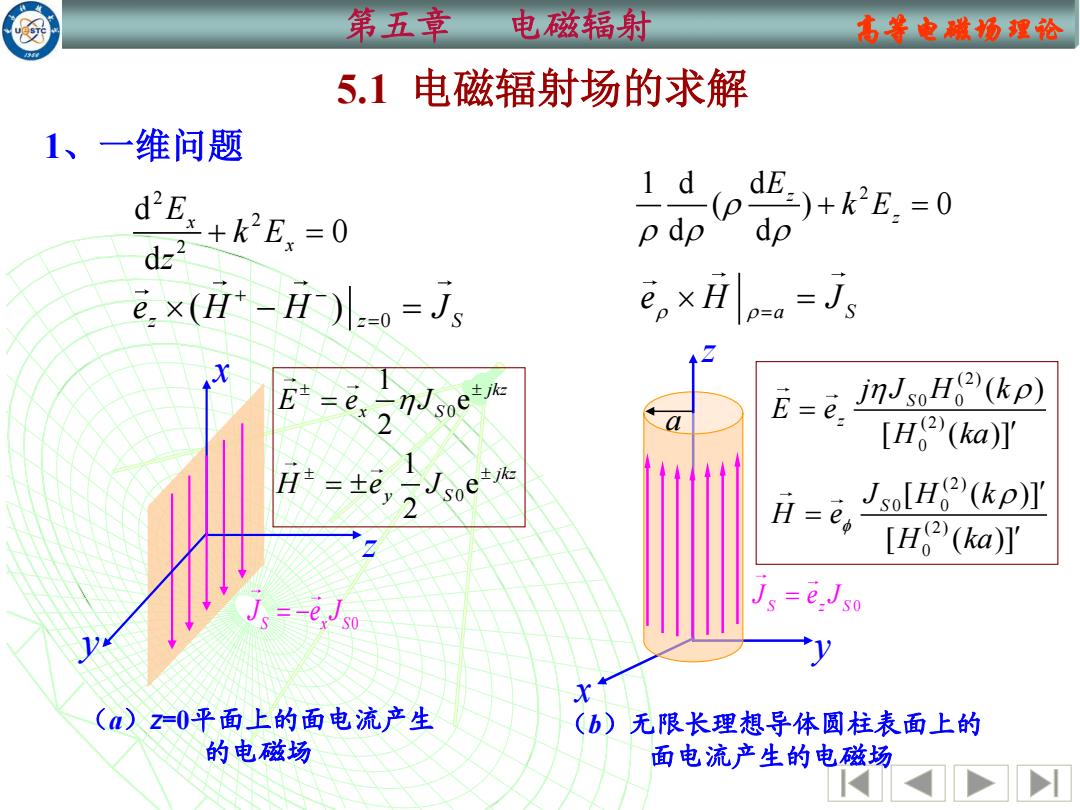
第五章 电磁辐射 名等电城场理论 5.1电磁辐射场的求解 1、一维问题 dE.+kE.-0 p dp dE)+E.=0 dz2 已×(H+-H0=Jj e。×Hlpa-jg E=2. nJsoH(kp) [H(ka)] *=e,2 H=e Jso[H(kp)] [H2(ka)] =e.Jso (a)z=0平面上的面电流产生 (b)无限长理想导体圆柱表面上的 的电磁场 面电流产生的电磁场

第五章 电磁辐射 高等电磁场理论 5.1 电磁辐射场的求解 1、一维问题 （a）z=0平面上的面电流产生 的电磁场 y S x S 0 J e J = − x z x S z S 0 J e J = y z a （b）无限长理想导体圆柱表面上的 面电流产生的电磁场 2 2 2 d 0 d x x E k E z + = 0 ( ) z z S e H H J + −  − = = 1 d d 2 ( ) 0 d d z z E  k E    + = a S e H J   =  = 0 1 e 2 jkz E e J x S    = 0 1 e 2 jkz H e J y S   =  ( 2 ) 0 0 ( 2 ) 0 ( ) [ ( )] S z j J H k E e H ka   =  ( 2 ) 0 0 ( 2 ) 0 [ ( )] [ ( )] S J H k H e H ka    = 

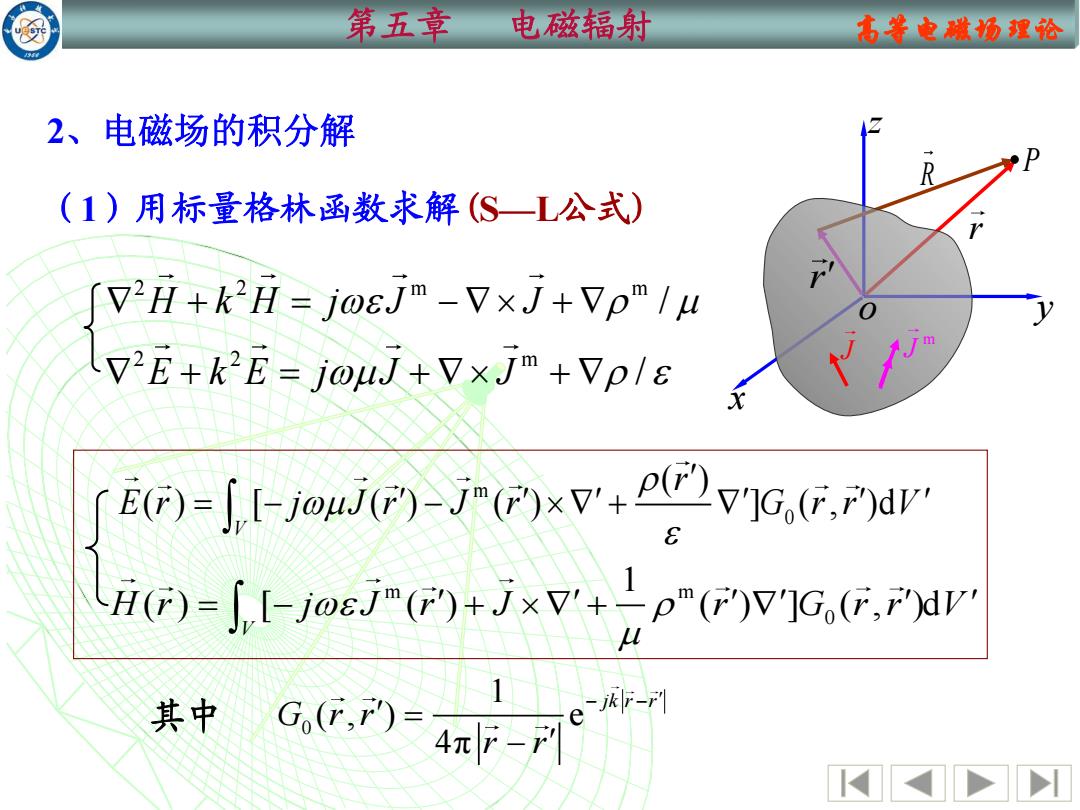
第五章 电磁辐射 名等电赋场理论 2、电磁场的积分解 R (1)用标量格林函数求解(S一L公式) V2H+k2H=josJm-VxJ+Vp"/u 72E+kE=j0μJ+V×Jm+Vp18 E(F)-fI-jouj()-j(xVIG(.F)av H(F)-fI-j@eJ-(P)+jxV+L"(F)V]G.(F.FXV 其中 GG,)=4πF-7 k-F1 e K

第五章 电磁辐射 高等电磁场理论 2 2 m m  + = −   +  H k H j J J   / 2 2 m  + = +   +  E k E j J J   / x y z o r r  R m J J P 2、电磁场的积分解 （1）用标量格林函数求解(S—L公式) 0 1 ( , ) e 4π jk r r G r r r r − −   = −  其中 m 0 ( ) ( ) [ ( ) ( ) ] ( , )d V r E r j J r J r G r r V      = − −   +         m m 0 1 ( ) [ ( ) ( ) ] ( , )d V H r j J r J r G r r V    = − +   +        

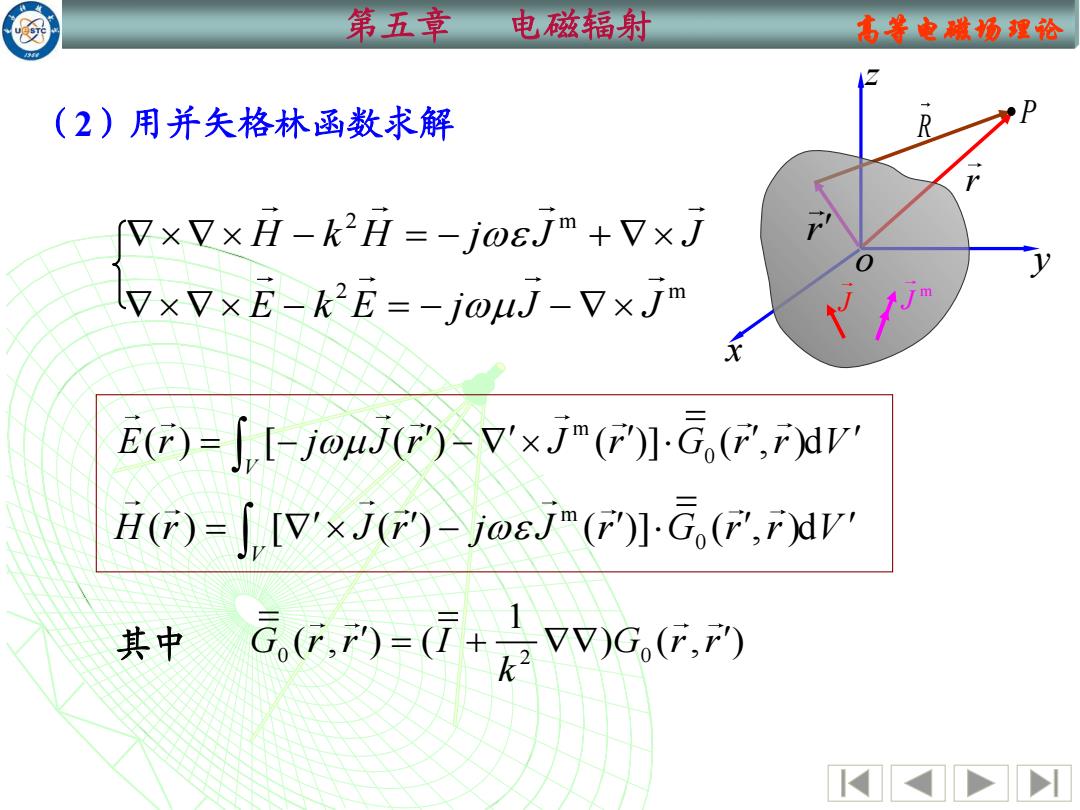
第五章 电磁辐射 古等电赋场理论 （2)用并矢格林函数求解 7×V×H-k2H=-j0ejm+V×j VxVxE-k2E=-jouj-Vxjm E(）=j[-j0ujF-V'×j严(G,(F,rw H(F)=∫[V'×j-joJj严(FG,(F,rdy 其中 )(GP)

第五章 电磁辐射 高等电磁场理论 m 0 ( ) [ ( ) ( )] ( , )d V E r j J r J r G r r V = − −            m 0 ( ) [ ( ) ( )] ( , )d V H r J r j J r G r r V =   −          （2）用并矢格林函数求解 0 0 2 1 G r r I G r r ( , ) ( ) ( , ) k 其中   = +  x y z o r r  R m J J P 2 m     − = − +   H k H j J J   2 m     − = − −   E k E j J J 

第五章 电磁辐射 名等电赋场理论 (3)用位函数求解 EF+0v利+0vx中 H-i产+月=xev4)+] u A(F)=J()G(F,)dv. A()=ε∫J严(F)G,(,F)d

第五章 电磁辐射 高等电磁场理论 （3）用位函数求解 x y z o r r  R m J J P e m 2 m 2 e m m 2 m 2 1 [ ( ) ] 1 [ ( ) ] j E E E A k A A k j H H H A A k A k      = + = −    + −       = + =   −    +  0 ( ) ( ) ( , )d , V A r J r G r r V =      m m 0 ( ) ( ) ( , )d V A r J r G r r V =     

第五章 电磁辐射 名等电赋场理论 3、Fraunhofer区和Fresenell☒ G) 1 。布-刊 F-手→G,,P1e 4πr 积分 不同相位波函数的叠加 k-=kvr2+r2-2rr'cosa kr1-2(r'/r)cosa 六3 =kr-kr'cosa+k-s cosa sin a+... 2r sin a+k 级近似：kF-≈kr-kr'Coso Fraunhofer☒ 二级近似：k|F-≈r-km'cosa+k。sin2a- 2r

第五章 电磁辐射 高等电磁场理论 积分 —— 不同相位波函数的叠加 0 1 ( , ) e 4π jk r r G r r r r − −   = −  2 2 k r r k r r rr − = + −    2 cos 2 3 2 2 2 cos sin cos sin 2 2 r r kr kr k k r r       = − + + +   − kr r r 1 2( / ) cos   1 1 r r r  −  一级近似： k r r kr kr −  −   cos 二级近似： 2 2 cos sin 2 r k r r kr kr k r    −  − +   —— Fraunhofer区 —— Fresenel区 0 1 ( , ) e 4π jk r r G r r r − −     x y z o r r  R m J J P 3、 Fraunhofer区和Fresenel区

第五章 电磁辐射 古等电城场理论 如何确定Fraunhofer区和Fresenel.区？ 要求：最大相位误差 2r 8 2r 8 入 Fresenel区： 六3 元 8 2π(D/2)32V5 元 a=arctan2→cos a sin2a=2√3/9 2r2 9 8 近区：00.62

第五章 电磁辐射 高等电磁场理论 要求：最大相位误差<π/ 8 2 3 2 2 2 cos sin cos sin 2 2 r r r r r r r r       −  − + + +   Fraunhofer区： 2 2 π sin 2 8 r k r    2 2π ( / 2) π 2 8 D  r   2 2D r   Fresenel区： 3 2 2 π cos sin 2 8 r k r      = arctan 2 3 2 2π ( / 2) 2 3 π 2 9 8 D  r      2  cos sin 2 3 / 9   = 3 0 0.62 D r    3 0.62 D r   近区： • 如何确定Fraunhofer区和Fresenel区？ x y z o r r  R m J J P

第五章 电磁辐射 名等电城场理论 5.2辐射场与辐射矢量 问题：如何求解分布在有限区域V内的源在远区(Fraunhofer.区) 产生的辐射场 E=∫[-jojG-jm×V'G。+2V'G,ldw' H(F)-[I-jm6j-G.+JxVG,+pYC, 由于 e(i)=-v.j(F) jo →E=j-joG,-j产xG。-(v-jpG,ar j08 =j,[-joG。-j严xV'G。+d.v'v'G1ar j08

第五章 电磁辐射 高等电磁场理论 5.2 辐射场与辐射矢量 问题：如何求解分布在有限区域 V 内的源在远区（Fraunhofer区） 产生的辐射场 m 0 0 0 ( ) [ ]d V E r j JG J G G V     =  + −   −     m m 0 0 0 1 ( ) [ ]d V H r j J G J G G V    = −  +  +      m 0 0 0 1 [ ( ) ]d V j JG J G J G V j     = −   +   −      1 ( ) ( ) r J r j   由于    = −   m 0 0 0 1 ( ) [ ( ) ]d V E r j JG J G J G V j      − = −   −        

第五章 电磁辐射 古等电赋场理论 对于远场区 kR>>1 -g眼 (J.V'7'G。≈-enk2(J.eR)Go →i=-mr-e+xK9ar 由 eR≈e, l/R≈l/rR≈r-e.·(Fraunhofer)☒) G0= ekR≈ e-jhelke 4元R 4元r -=Uo-i碳+)ijp

第五章 电磁辐射 高等电磁场理论 0 R  jkG e 对于远场区 2 0 0 ( ) ( ) R R J G e k J e G    −   kR  1 0 0 0 1 1 ( ) (1 ) R R G jk G e jk G R jkR R   = + = +  m 0 0 0 1 ( ) [ ( ) ]d V E r j JG J G J G V j     = −   +  −       m 0 ( ) [ ( ) ] d R R R V E r j J J e e J e G V      + = − −     R r e e  1/ 1/ R r  R r e r r 由  −   0 1 1 e e e 4π 4π r jkR jkr jke r G R r − −   =  （Fraunhofer区） m ( ) e [ ( ) ( ) ( ) ]e d 4 r jkr jke r r r r V j E r J r J r e e J r e V r     −   = − −       + 