中国科学技术大学：《电磁学》课程教学资源（课件讲稿）第四章 稳恒电流

第四章稳恒电流 §4.1稳恒条件 §4.2欧姆定律与焦耳定律 §4.3电源与电动势 §4.4基尔霍夫定律 *§4.5稳恒电流与静电场的综合求解

第四章 稳恒电流 §4.1 稳恒条件 §4.2 欧姆定律与焦耳定律 §4.3 电源与电动势 §4.4 基尔霍夫定律 *§4.5 稳恒电流与静电场的综合求解

基本知识 在用金属导线转移电荷中，人们认识到电 荷的定向移动，开始了这种现象的研究。 电流的定义：在导体中，电荷的定向运动就 是电流 。 稳恒电流的定义：不随时间变化的电流即稳 恒电流。 有稳恒电流时导体的状况：导体中自由电荷 的分布不会随时间变化，所产生的电场也不 随时间变化，称为恒定电场，即导体内存在 着非零的电场，这电场保证了电流，而且：

基本知识 在用金属导线转移电荷中，人们认识到电 荷的定向移动，开始了这种现象的研究。 n 电流的定义：在导体中，电荷的定向运动就 是电流。 n 稳恒电流的定义：不随时间变化的电流即稳 恒电流。 n 有稳恒电流时导体的状况：导体中自由电荷 的分布不会随时间变化，所产生的电场也不 随时间变化，称为恒定电场，即导体内存在 着非零的电场，这电场保证了电流，而且：

(1) 电流既是电荷的运动，它本身满足电荷守 恒定律 。 (2) 导体内恒定电场与电流之间的依懒关系满 足一定的实验规律，该规律反映了导体的 导电性质； (3) 恒定电场本质上属于静电场，同样满足静 电场的基本规律，以下将不加区别地将恒 定电场称为静电场： 具有稳恒电流的导体的状态与处于静电平衡 的导体状态是截然不同的。处于静电平衡的导体 状态表现为导体内电场强度必须处处为零

n (1) 电流既是电荷的运动，它本身满足电荷守 恒定律。 n (2) 导体内恒定电场与电流之间的依赖关系满 足一定的实验规律，该规律反映了导体的 导电性质； n (3) 恒定电场本质上属于静电场，同样满足静 电场的基本规律，以下将不加区别地将恒 定电场称为静电场； n 具有稳恒电流的导体的状态与处于静电平衡 的导体状态是截然不同的。处于静电平衡的导体 状态表现为导体内电场强度必须处处为零

§4.1稳恒条件 电流强度和电流密度 二、 电流的物理图像 三、 电流连续方程 闪、 稳恒条件

§4.1 稳恒条件 一 、 电流强度和电流密度 二、 电流的物理图像 三、 电流连续方程 四、 稳恒条件

电流强度和电流密度 ■中学里接触到直流电路的时候，曾引入电流强度： △q (4.1.1) △t 电流强度的单位为库仑/秒，称为安[培]，符号为A。 用电流强度描述导体中电荷的宏观流动性质似乎太 “粗糙”。 (1)不能描述电流沿载面的分布情况； (2)不能描述电流的方向，即正电荷移动的方向。 ■为了描述导体中各点电流的大小和方向，人们引入 一个更“精细”的物理量—一电流密度

一 、 电流强度和电流密度 ■ 中学里接触到直流电路的时候，曾引入电流强度： . q I t    (4.1.1) 电流强度的单位为库仑/秒，称为安[培]，符号为A。 ■ 用电流强度描述导体中电荷的宏观流动性质似乎太 “粗糙” 。（1）不能描述电流沿截面的分布情况； （2）不能描述电流的方向，即正电荷移动的方向。 ■ 为了描述导体中各点电流的大小和方向，人们引入 一个更“精细”的物理量——电流密度

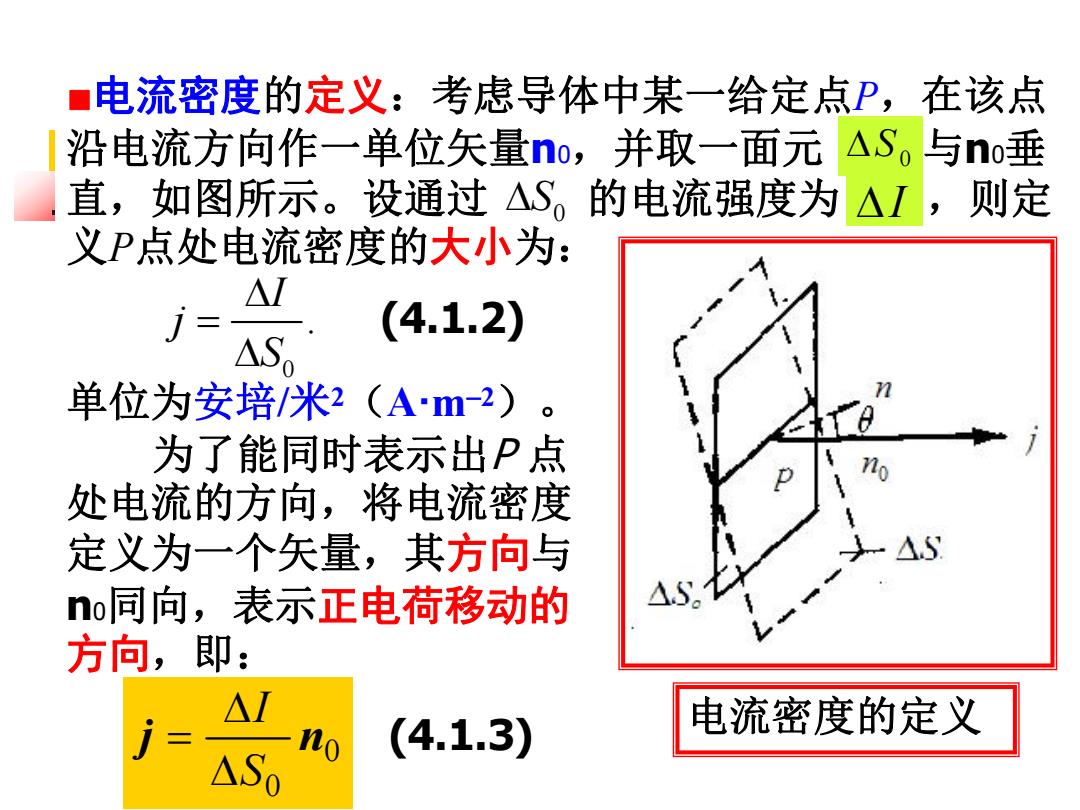
■电流密度的定义：考虑导体中某一给定点P,在该点 沿电流方向作一单位矢量no,并取一面元△S。与n垂 直，如图所示。设通过△S。的电流强度为△1，则定 义P点处电流密度的大小为： △I (4.1.2) △S 单位为安培米2（Am-2) 为了能同时表示出P点 处电流的方向，将电流密度 定义为一个矢量，其方向与 4.5 no同向，表示正电荷移动的 方向，即： △I no (4.1.3) 电流密度的定义 ASo

■电流密度的定义：考虑导体中某一给定点P，在该点 沿电流方向作一单位矢量n0，并取一面元 与n0垂 直，如图所示。设通过 的电流强度为 ，则定 义P点处电流密度的大小为： 0 . I j S    (4.1.2) 电流密度的定义 单位为安培/米2（A·m2）。 为了能同时表示出P 点 处电流的方向，将电流密度 定义为一个矢量，其方向与 n0同向，表示正电荷移动的 方向，即： 0 S 0 S I 0 0 j n S I    (4.1.3)

由上述定义可见，电流密度是一个矢量，它的方向 表示导体中某点电流的方向，数值等于通过垂直于该 点电流方向的单位面积的电流强度。 这样定义的电流密度是空间位置的矢量函数()， 它细致地描述了导体中的电流分布，也称为电流场 。 类似静电场，对电流场也可以通过引入“电流线 来进行形象描述。电流线即电流所在空间的一组曲线， 其上任一点的切线方向和该点的电流密度方向一致。 一束这样的电流线围成的管状区域称为电流管。 已知导体中某点P的电流密度，可求得通过该点任 一面元AS的电流强度AM=jS,=j△S'cos.(见上页图) 又可写成△=i△S. 通过S面的电流强度I V=八s方& (4.1.4)

■ 由上述定义可见，电流密度是一个矢量，它的方向 表示导体中某点电流的方向，数值等于通过垂直于该 点电流方向的单位面积的电流强度。 这样定义的电流密度是空间位置的矢量函数j(r)， 它细致地描述了导体中的电流分布，也称为电流场。 ■ 类似静电场，对电流场也可以通过引入“电流线” 来进行形象描述。电流线即电流所在空间的一组曲线， 其上任一点的切线方向和该点的电流密度方向一致。 一束这样的电流线围成的管状区域称为电流管。 ■ 已知导体中某点P的电流密度，可求得通过该点任 一面元 的电流强度 （见上页图） 又可写成 S 0 I  jS  jS cos. I  j S. . S I  d  通过 S 面的电流强度I ： j S (4.1.4)

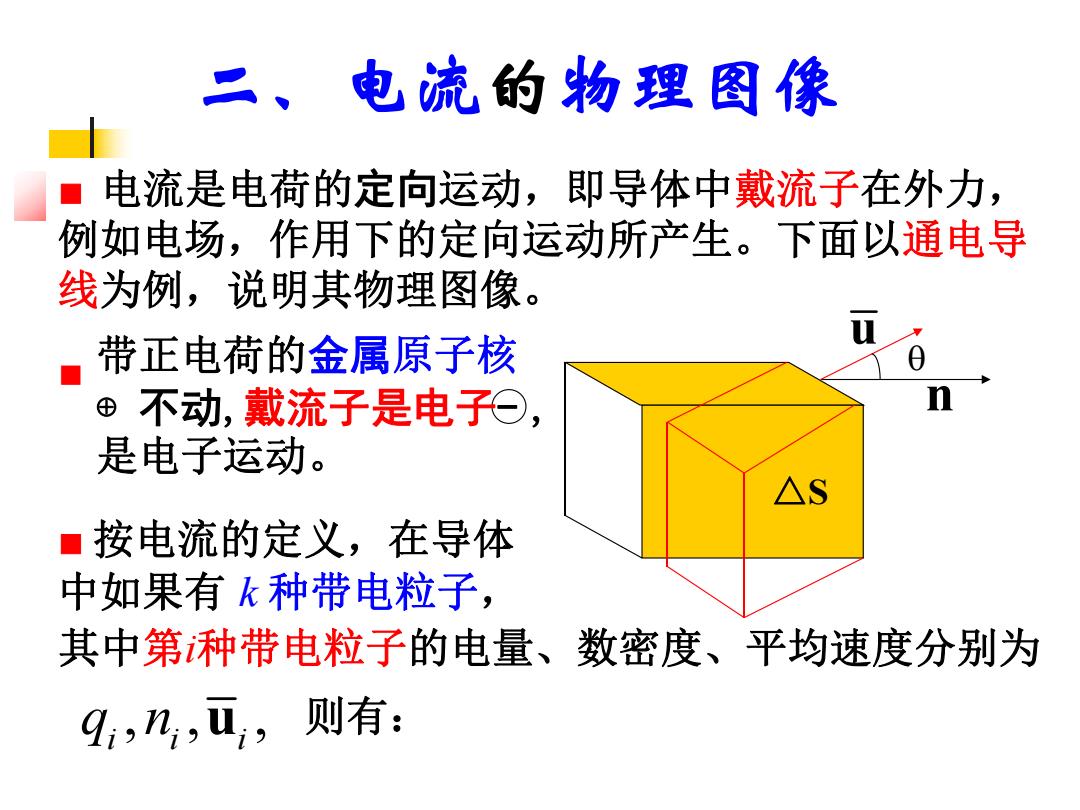
二、电流的物理图像 ■电流是电荷的定向运动，即导体中戴流子在外力， 例如电场，作用下的定向运动所产生。下面以通电导 线为例，说明其物理图像。 带正电荷的金属原子核 ⊕不动，戴流子是电子⊙， 是电子运动。 ■按电流的定义，在导体 中如果有k种带电粒子， 其中第种带电粒子的电量、数密度、平均速度分别为 9,n,ū，则有：

二、电流的物理图像 ■ 电流是电荷的定向运动，即导体中戴流子在外力， 例如电场，作用下的定向运动所产生。下面以通电导 线为例，说明其物理图像。 △S n  u ■ ■ 按电流的定义，在导体 中如果有 k 种带电粒子， 带正电荷的金属原子核 ⊕ 不动,戴流子是电子- , 是电子运动。 其中第i种带电粒子的电量、数密度、平均速度分别为 , , , i i i q n u 则有：

AM=立gi,AS=2P.,AS i=l i=l AI=j·△S .j厉2P,=2gn如 i=l i=l ■在戴流金属 导线中只有两 2A=R.+P.-0 整体电中性 种带电粒才： i=l j兰ped+p。-ū=p.-ū=-enu ≠0 ■ 当不戴流 金属导线整 +=ū，.j=u(P,+见)=0 体运动时：

1 1 k k i i i ei i i i I q n       u  S   u  S ■ 在戴流金属 导线中只有两 种带电粒子： 2 1 0, ei e e i          整体电中性 0. e e e    en j  u  u  u   u  ■ 当不戴流 金属导线整 体运动时： ( ) 0.  ju e e  0 ,  u  u 1 1 k k ei i i i i i i q n I             j S j u u 

[例]一般戴流金属导线中的情况。 j~10安培/米2， n~1029/米3， g=e~1019库仑. .'j=-enū→ io 06 )、109×102~10(米/秒). 可见电子的平均定向速度是很慢的，但为何电源一接 通立即灯亮呢？这是由于电场的传播速度为光速C

[例] 一般戴流金属导线中的情况。 6 29 3 19 ~ 10 , ~ 10 / , ~ 10 . j n q e   安培 2 /米 米 库仑 可见电子的平均定向速度是很慢的，但为何电源一接 通立即灯亮呢？这是由于电场的传播速度为光速C。 6 4 19 29 10 ~ ~ 10 ( / ). 10 10 en j en           j u u 米 秒 