
第三章 电阻电路的一般分析 内容提要 电路的一般分析是指方程分析法,它是以电路元件 的约束特性(VCR)和电路的拓扑约束特性(KCL、 KVL)为依据,建立以支路电流或回路电流,或结点电 压为变量的电路方程组,从中解出所要求的电流、电压 等。 本章介绍线性电阻电路方程的建立方法。内容包 括:支路电流法,网孔法,回路法和结点法
第三章 电阻电路的一般分析 内容提要 电路的一般分析是指方程分析法,它是以电路元件 的约束特性(VCR)和电路的拓扑约束特性(KCL、 KVL)为依据,建立以支路电流或回路电流,或结点电 压为变量的电路方程组,从中解出所要求的电流、电压 等。 本章介绍线性电阻电路方程的建立方法。内容包 括:支路电流法,网孔法,回路法和结点法

目录 §3一3支路电流汽 §3一4、5网孔、回路电流 一6结点电压 法
目录 §3 — 3 支路电流法 §3 — 4、5 网孔、回路电流 法 §3 — 6 结点电压 法
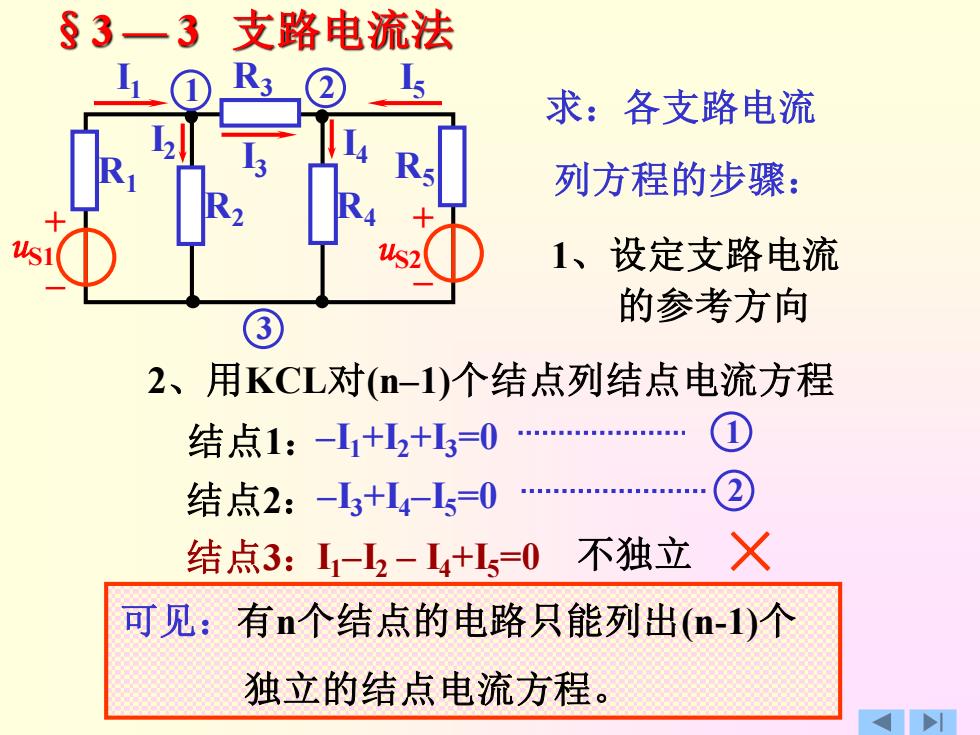
§3一3支路电流法 ① R3 ② 求:各支路电流 列方程的步骤: 1、设定支路电流 的参考方向 2、用KCL对(n-1)个结点列结点电流方程 结点1:+2+0 结点2:-3+L4-I=0 结点3:1-2-L+1=0不独立X 可见:有n个结点的电路只能列出(n-1)个 独立的结点电流方程
§3 — 3 支路电流法 + – + – uS1 R1 R2 R3 R4 R5 uS2 求:各支路电流 列方程的步骤: 1、设定支路电流 的参考方向 I1 I2 I3 I4 I5 2、用KCL对(n–1)个结点列结点电流方程 1 2 3 结点1:–I1+I2+I3=0 结点2:–I3+I4–I5=0 结点3:I1–I2 – I4+I5=0 可见:有n个结点的电路只能列出(n-1)个 独立的结点电流方程。 1 2 不独立 ×
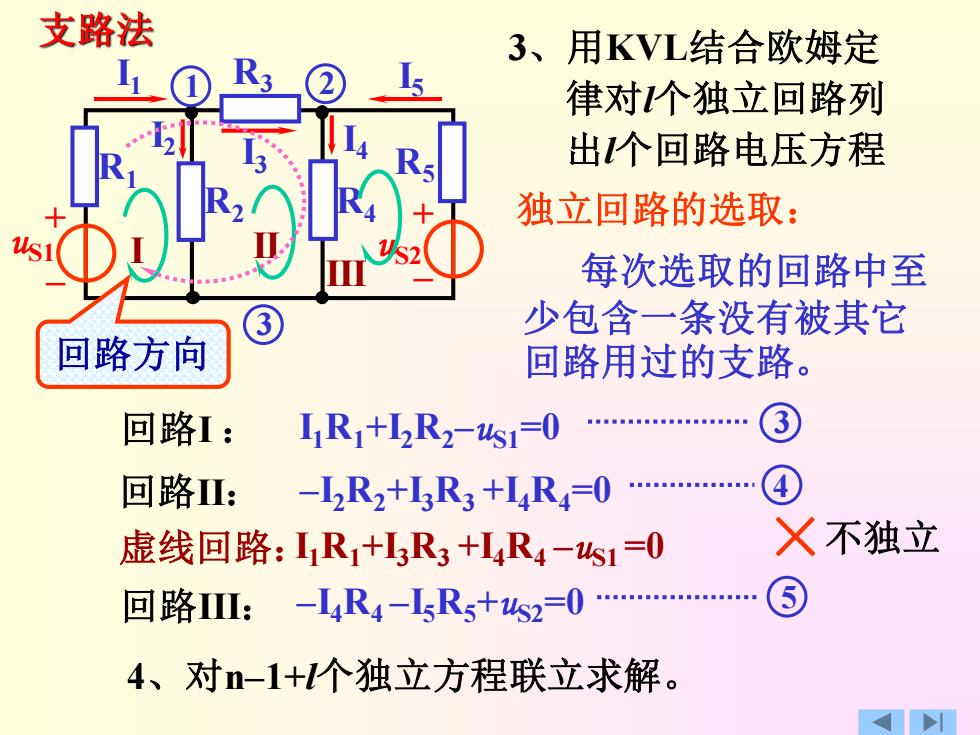
支路法 3、用KVL结合欧姆定 律对个独立回路列 出个回路电压方程 独立回路的选取: 每次选取的回路中至 少包含一条没有被其它 回路方向 回路用过的支路。 回路1: IR+R2-us1=0 回路:-R2+5R3+L4R40 虚线回路:R+R3+L4R4-s1=0 义不独立 回路:-R4-5R5十s2=0. 4、对n-1+个独立方程联立求解
支路法 3、用KVL结合欧姆定 律对l个独立回路列 出l个回路电压方程 I1R1+I2R2–uS1=0 回路II: 回路I : 回路III: –I2R2+I3R3 +I4R4=0 虚线回路:I1R1+I3R3 +I4R4 –uS1 =0 –I4R4 –I5R5+uS2=0 + – + – uS1 R1 R2 R3 R4 R5 uS2 I1 I2 I3 I4 I 1 2 5 3 I II III 5 3 4 ×不独立 独立回路的选取: 每次选取的回路中至 少包含一条没有被其它 回路用过的支路。 4、对n–1+l个独立方程联立求解。 回路方向
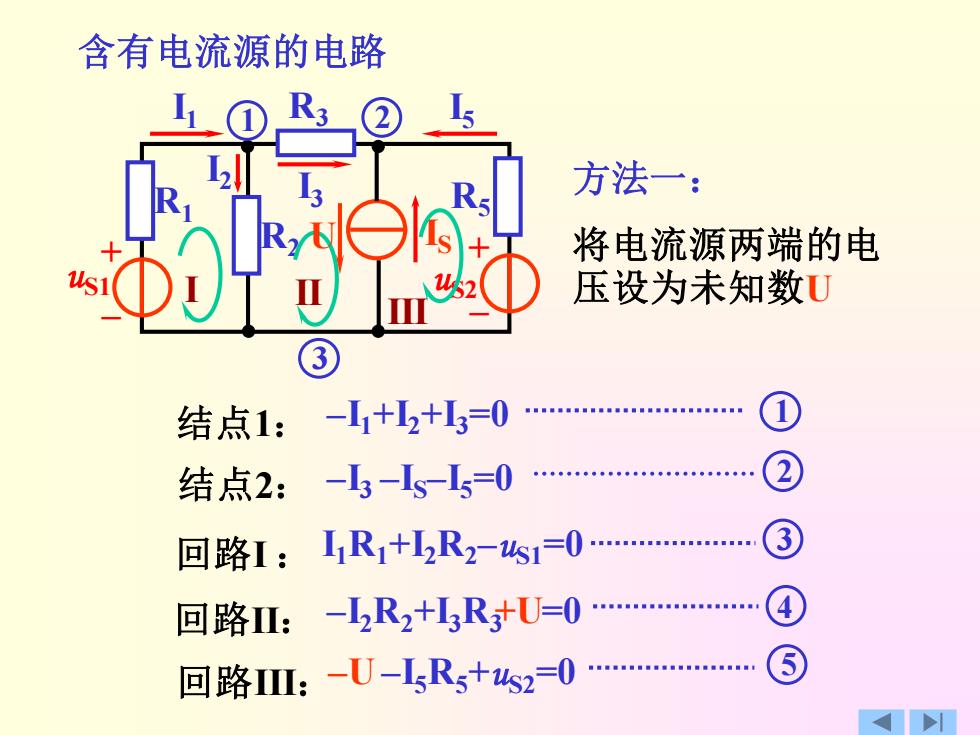
含有电流源的电路 1① R3 方法一: 将电流源两端的电 压设为未知数U 3 结点1:-+2+3=0 结点2:-3-1s-1=0 %. 回路1:R+2R2-1=0. 回路Ⅲ:-R2+HR+U=0 回路:-U-IR5+s2=0
含有电流源的电路 + – + – uS1 R1 R2 R3 R5 uS2 I1 I2 I3 IS I 1 2 5 3 方法一: 结点1: –I1+I2+I3=0 1 结点2: –I3 –IS–I5=0 2 I1R1+I 回路 2R2–uS1=0 I : 3 I II III 回路II: –I2R2+I3R3 =0 4 U +U 回路III:–U –I5R5+uS2=0 5 将电流源两端的电 压设为未知数U
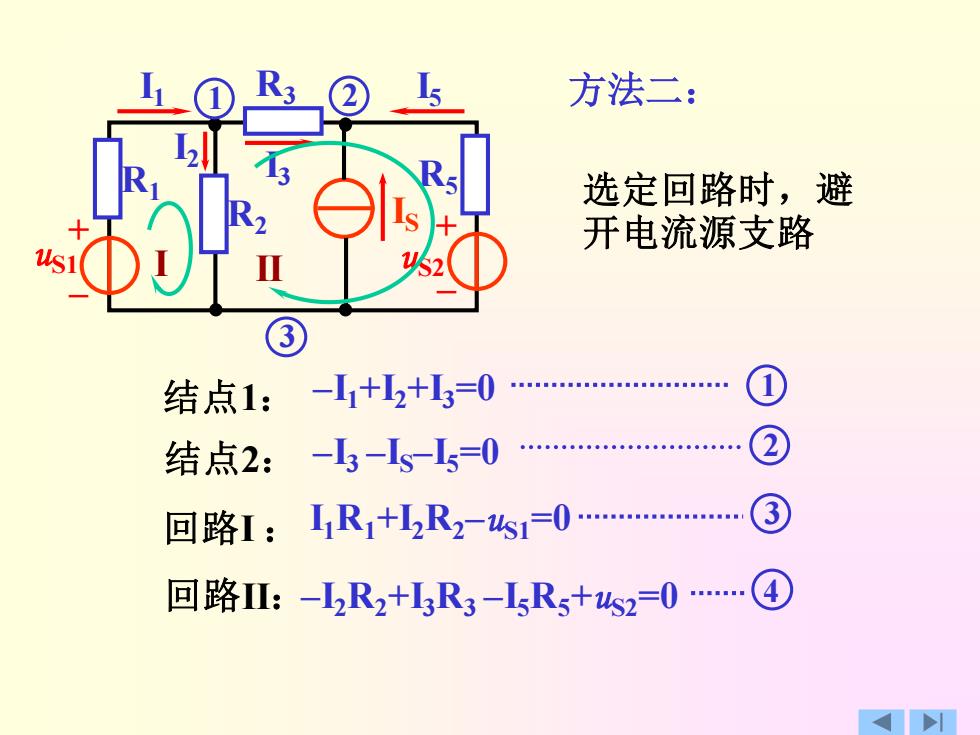
R3 方法二: 选定回路时,避 开电流源支路 ③ 结点1:-++=0 结点2:-3-s-L50 回路I:R1+2R2-W1=0. 3 回路l:-2R2+3R3-5R+s2=0 .④
方法二: + – + – uS1 R1 R2 R3 R5 uS2 I1 I2 I3 IS I 1 2 5 3 I II 选定回路时,避 开电流源支路 回路II:–I2R2+I3R3 –I5R5+uS2=0 4 结点1: –I1+I2+I3=0 1 结点2: –I3 –IS–I5=0 2 I1R1+I 回路 2R2–uS1=0 I : 3
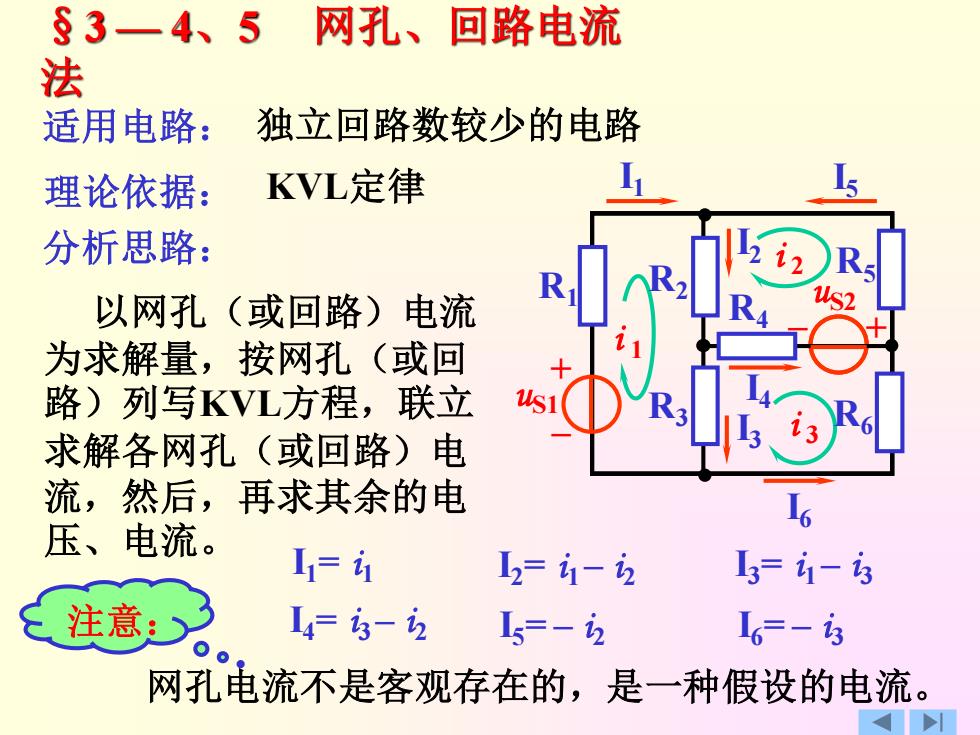
§3-4、5 网孔、回路电流 法 适用电路: 独立回路数较少的电路 理论依据: KVL定律 分析思路: 2)R 以网孔(或回路)电流 为求解量,按网孔(或回 路)列写KVL方程,联立 求解各网孔(或回路)电 流,然后,再求其余的电 压、电流。 1= 12=-2 =1-3 注意:> 4=3-2 L5=-2 L6=-3 网孔电流不是客观存在的,是一种假设的电流
§3 — 4、5 网孔、回路电流 法 理论依据: KVL定律 分析思路: 以网孔(或回路)电流 为求解量,按网孔(或回 路)列写KVL方程,联立 求解各网孔(或回路)电 流,然后,再求其余的电 压、电流。 适用电路: 独立回路数较少的电路 i 1 i 2 i 3 I1= i1 I2= i1 – i2 I3= i1 – i3 I4= i3 – i2 I5= – i2 I6= – i3 网孔电流不是客观存在的,是一种假设的电流。 – + + – uS1 I1 R1 R2 R3 R4 R5 R6 uS2 I2 I3 I4 I5 I6 注意:
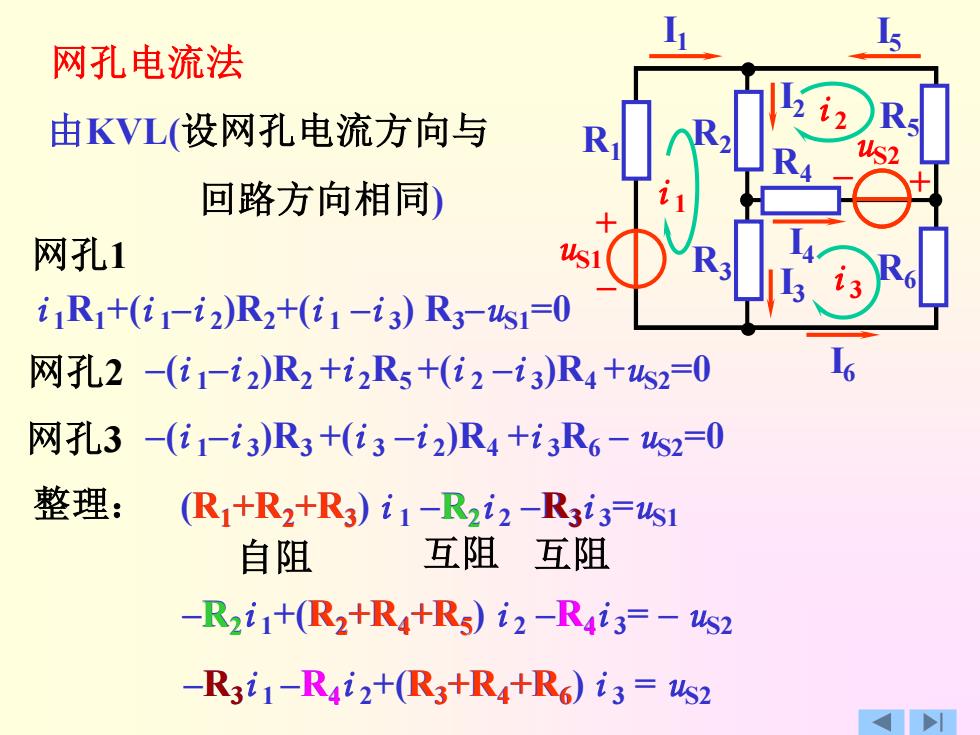
网孔电流法 由KVL(设网孔电流方向与 R 1S2 回路方向相同) 网孔1 iiR1+(i1-i2)R2+(i1-i3)R3-s10 网孔2-(i1-i2)R2+i2Rs+i2-i3)R4+s2=0 网孔3(i1-i3)R3+(i3-i2)R4+i3R6-s20 整理: (R+R2+R3)i1-R2i2-R3i3=us1 自阻 互阻互阻 -R2i1+(R2+R4+Rs)i2-R4i3=-ks2 -R3i1-R4i2+(R3+R4+R6)i3=us2
网孔电流法 由KVL(设网孔电流方向与 回路方向相同) 网孔1 i 1R1+(i 1–i 2 )R2+(i 1 –i 3 ) R3–uS1=0 网孔2 –(i 1–i 2 )R2 +i 2R5 +(i 2 –i 3 )R4 +uS2=0 网孔3 –(i 1–i 3 )R3 +(i 3 –i 2 )R4 +i 3R6 – uS2=0 整理: (R1+R2+R3 ) i 1 –R2 i 2 –R3 i 3=uS1 –R2 i 1+(R2+R4+R5 ) i 2 –R4 i 3= – uS2 –R3 i 1 –R4 i 2+(R3+R4+R6 ) i 3 = uS2 R1+R2+R3 R2+R4+R5 R3+R4+R6 R2 R2 R3 R3 自阻 互阻 互阻 – + + – uS1 I1 R1 R2 R3 R4 R5 R6 uS2 I2 I3 I4 I5 I6 i 1 i 2 i 3 R4 R4

回路电流法 回路1 (i1ti3)R+(i1-i2)R2+iR3-w1=0 is? 回路2 (i2-i1)R2+(i2+i3)R5+R4i2+s2=0 回路3 (i1+i3)R+(i2+i3)Rs+i3R6-s1=0 整理: 回路1(R+R2+R3)i1-R2i2+R1i3=s1 自阻 互阻互阻 回路2-R2i1+(R2+R+Rs)i2+Rsi3=-s2 回路3R1i1+Rsi2+(R+RtR6)i3=s1 自阻一与所选网孔(回路)有关的电阻之和,总为正。 互阻 与相关网孔共含的电阻之和,可正可负
回路电流法 – + + – uS1 I1 R1 R2 R3 R4 R5 R6 uS2 I2 I3 I4 I5 I6 i 1 i 2 i 回路 3 1 (i 1+i 3 )R1+(i 1–i 2 )R2+i 1R3–uS1=0 回路2 (i 2–i 1 )R2+(i 2+i 3 )R5+R4 i 2+uS2=0 回路3 (i 1+i 3 )R1+(i 2+i 3 )R5+i 3R6–uS1=0 整理: 回路1 (R1+R2+R3 ) i 1 –R2 i 2 +R1 i 3=uS1 回路2 –R2 i 1+(R2+R4+R5 ) i 2 +R5 i 3= – uS2 回路3 R1 i 1 +R5 i 2+(R1+R5+R6 ) i 3 =uS1 自阻 互阻 互阻 自阻——与所选网孔(回路)有关的电阻之和,总为正。 互阻——与相关网孔共含的电阻之和,可正可负

网孔(回路)方程的一般表达式: R1i+R12i2+R13i3=s11R11R22、R33自阻(总为正) R21i+Rn2+R222R12R2R8互阻(可正可负) R31i+R32i2+R33i3=s33R31R23、R32 电路中不含受控源时:R12=R21R23=R32R13=R31 两网孔(回路)电流流过该电阻时电流方向相同, 互阻为正。 两网孔(回路)电流流过该电阻时电流方向相反, 互阻为负。 当网孔电流方向选择一致时,互阻总为负。 s11、1s22、S33 回路中电压源电压的代数和
网孔(回路)方程的一般表达式: R11i 1+R12i 2+R13i 3= uS11 R21i 1+R22i 2+R23i 3= uS22 R31i 1+R32i 2+R33i 3= uS33 R11、R22、R33 R12、R21、R13 R31、R23、R32 互阻(可正可负) 两网孔(回路)电流流过该电阻时电流方向相同, 互阻为正。 两网孔(回路)电流流过该电阻时电流方向相反, 互阻为负。 电路中不含受控源时: R12=R21 R23=R32 R13=R31 自阻(总为正) 当网孔电流方向选择一致时,互阻总为负。 uS11、 uS22 、uS33 回路中电压源电压的代数和