
第四章 电路定律 内容提要 电路定理是电路理论的重要组成部分,为我们 求解电路问题提供了另一种分析方法,这些方法具 有比较灵活,变换形式多样,目的性强的特点。 本章介绍的电路定理包括叠加定理(齐性定理)、 替代定理、戴维宁定理和诺顿定理
第四章 电路定律 内容提要 电路定理是电路理论的重要组成部分,为我们 求解电路问题提供了另一种分析方法,这些方法具 有比较灵活,变换形式多样,目的性强的特点。 本章介绍的电路定理包括叠加定理(齐性定理)、 替代定理、戴维宁定理和诺顿定理

目录 §4一1叠加定理 §4一2替代定 理 §4一3戴维宁定理和诺顿定 理
目录 § 4 — 1 叠加定理 § 4 — 2 替代定 理 § 4 — 3 戴维宁定理和诺顿定 理
§4一1叠加定理 线性电路的重要性质 R 求:=? 解:由网孔法 (R+R2)I+R2Is+uI=Us 1 R2 I-R,+R,FHUs-R:+R,+us =l0四+2) 1 R:+R2+uUs 只与激励Us有关, 与Ls无关(Is=0)
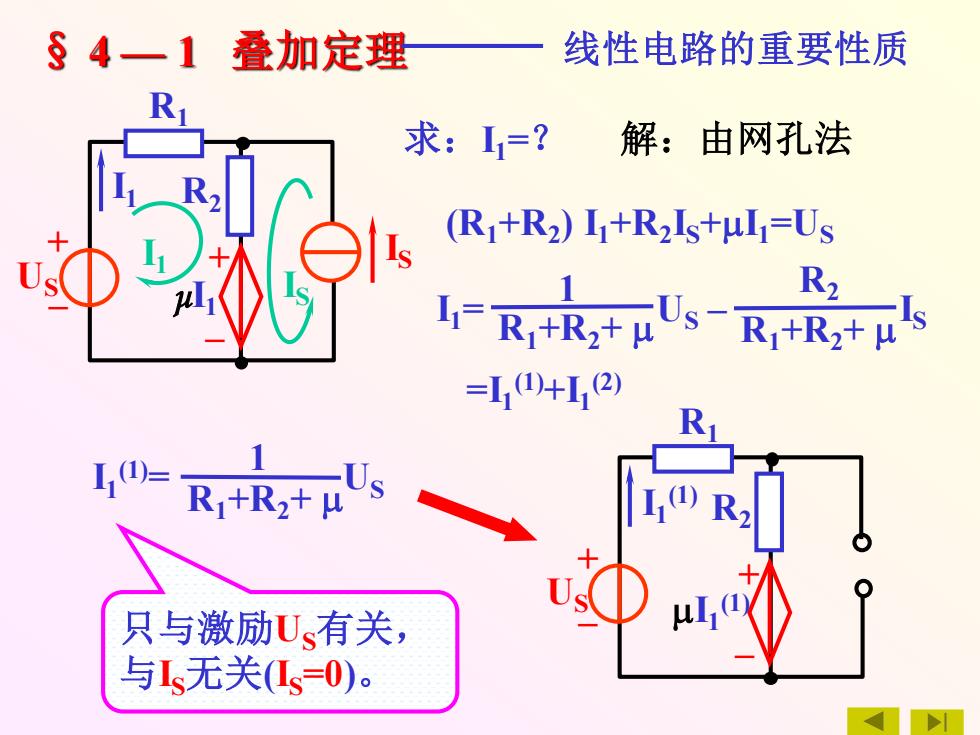
§ 4 — 1 叠加定理 线性电路的重要性质 + – + – US IS R1 μI1 R2 I1 求:I1=? I1 IS 解:由网孔法 (R1+R2 ) I1+R2 IS+I1=US I1= US – IS 1 R1+R2+ R2 R1+R2+ 1 R1+R2+ I1 (1)= US 只与激励US有关, 与IS无关(IS=0)。 + – + – US R1 I1 (1) R2 I1 (1) =I1 (1)+I1 (2)
叠加定理 R2 4-R+R+ 只与激励Ls有关, 与Us无关(Us-0). R I)R2
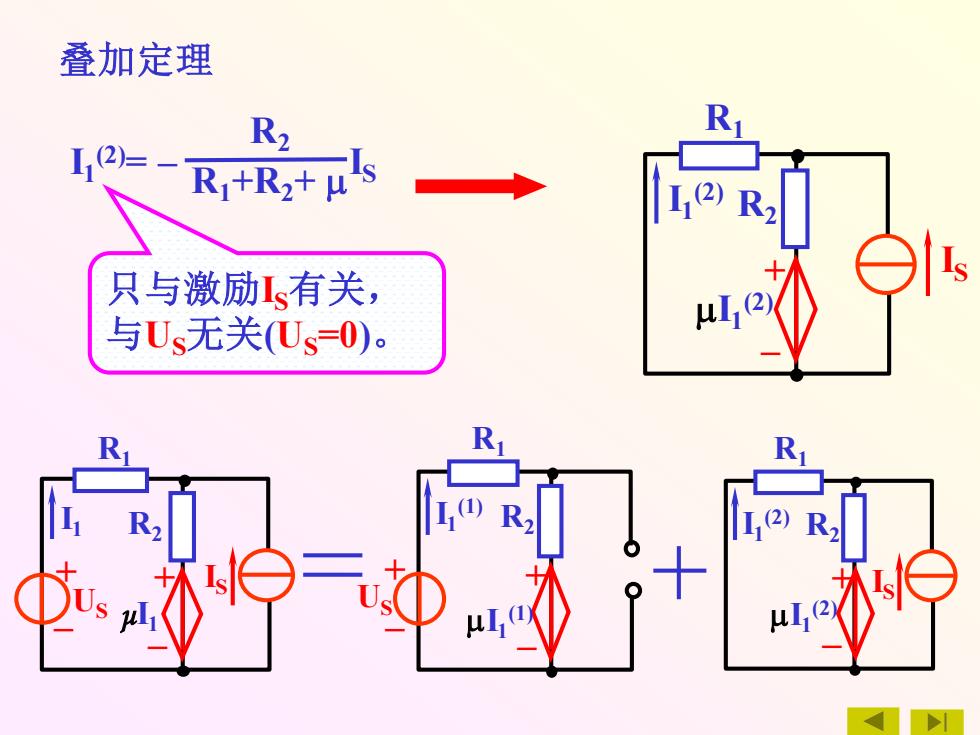
叠加定理 + – + – US IS R1 μI1 R2 I1 R2 R1+R2+ I1 (2)= – IS 只与激励IS有关, 与US无关(US=0)。 + – IS R1 I1 (2) R2 I1 (2) + – + – US R1 I1 (1) R2 I1 (1) + – IS R1 I1 (2) R2 I1 (2)

叠加定理: 在线性电路中,任一电压或电流都是电路中各 个独立电源单独作用时,在该处产生的电压或电流 的叠加。 如上例: RRsR5ksK, R2 一般表达式: X-akUsk+BqIsa K=1
叠加定理: 在线性电路中,任一电压或电流都是电路中各 个独立电源单独作用时,在该处产生的电压或电流 的叠加。 如上例: I1= US – IS= K1US+K2 IS 1 R1+R2+ R2 R1+R2+ 一般表达式: X= KUSK+ q ISq K=1 n m q=1

注意事项: 1、叠加定理只适用于线性电路,不能用于非线性电路。 2、利用叠加定理只能用来计算线性电路的电压或电流, 不能用来计算功率。 =I)+I2) R P=PR=[I()+I22RI()2R+I@2)2R=P()+P() 3、注意单个独立源激励时响应的参考方向,叠加时是 求代数和(有“+”有“_”)。 4、单个独立源作用时,不参与作用的其余电压源作短 路处理,电流源作断路处理。 5、分析含有受控源的电路时,受控源不能单独作用。 各个独立源作用时,受控源都必须保留在电路中
注意事项: 1、叠加定理只适用于线性电路,不能用于非线性电路。 2、利用叠加定理只能用来计算线性电路的电压或电流, 不能用来计算功率。 R I I=I(1)+I(2) P=I2R=[I(1)+I(2)] 2R I (1)2R+I(2)2R=P(1)+P(2) 3、注意单个独立源激励时响应的参考方向,叠加时是 求代数和(有“+”有“–”)。 4、单个独立源作用时,不参与作用的其余电压源作短 路处理,电流源作断路处理。 5、分析含有受控源的电路时,受控源不能单独作用。 各个独立源作用时,受控源都必须保留在电路中
例1: 用叠加定理求: 2 U和及32电阻消耗的功率 解:1V电压源单独作用; U0)=0 I=0.5A 3A U2)=1.5V I2)=1A
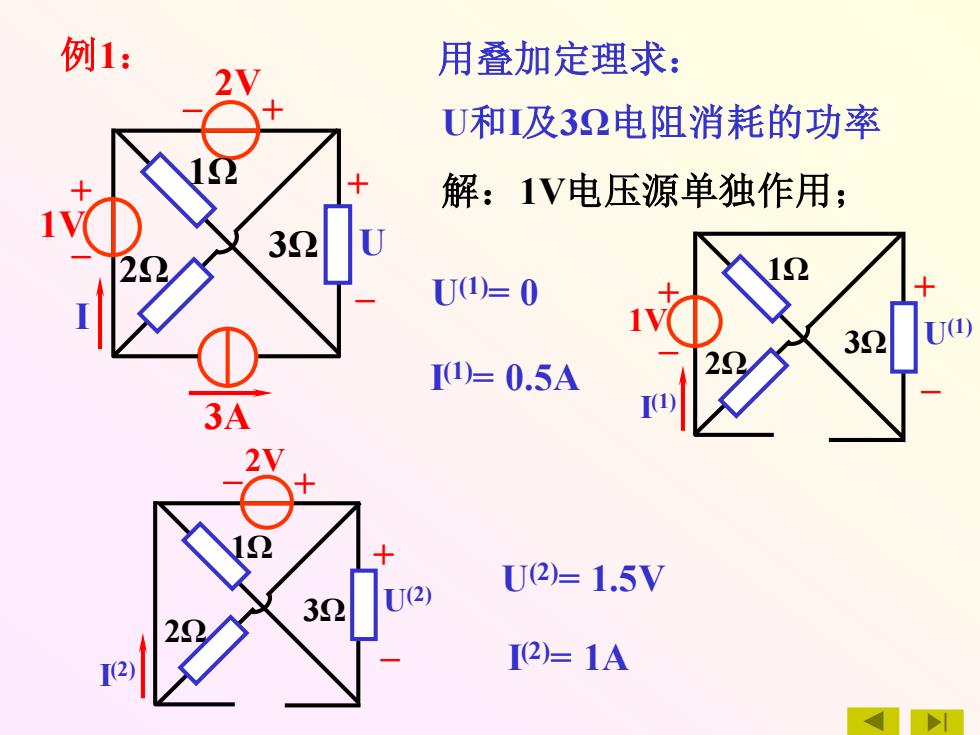
例1: – + + – 1Ω – + U I 3A 1V 2V 2Ω 3Ω 用叠加定理求: U和I及3Ω电阻消耗的功率 解:1V电压源单独作用; 1Ω U(1) I (1) 1V 2Ω + – – + 3Ω U(1)= 0 I (1)= 0.5A 1Ω U(2) I (2) 2V 2Ω – + – + 3Ω U(2)= 1.5V I (2)= 1A
续例1:3A电流源单独作用; 24 32 3A 3A U3)=-2.25V I3)=-3A 叠加 =I)+I2)+I3)=0.5+1-3=-1.5A U=U1)+U2)+U3)=0+1.5-2.25=-0.75V a号-4719y 3 P3n≠02+U22+UB2 2.44W 3 3 3
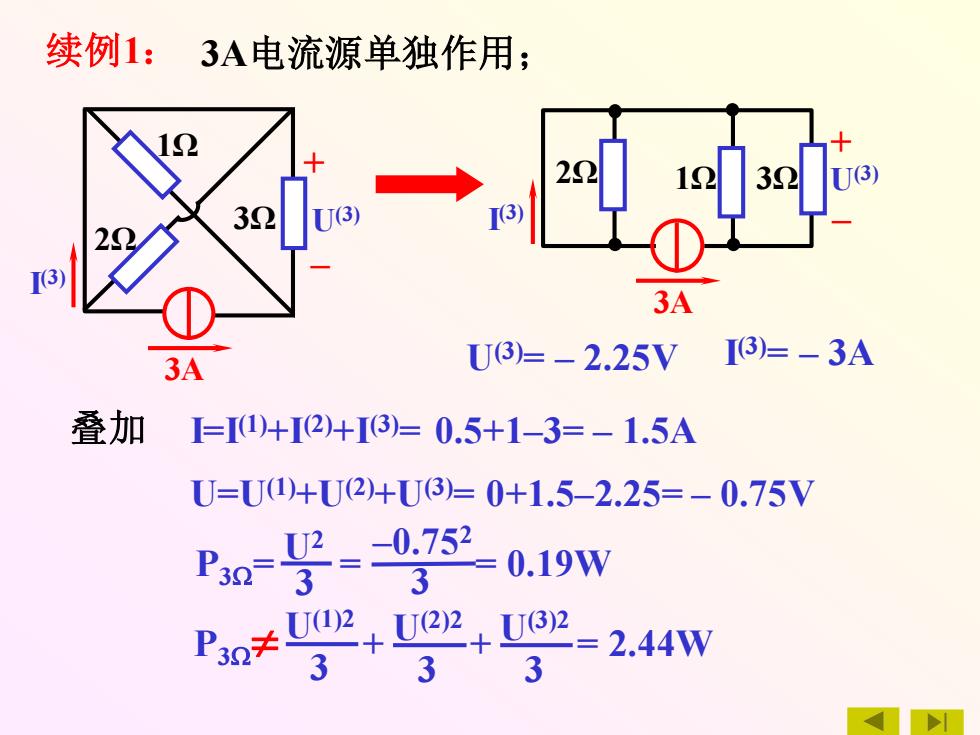
续例1: 3A电流源单独作用; 1Ω U(3) I (3) 2Ω – + 3Ω 3A 3A 2Ω 1Ω 3Ω I (3) + – U(3) U(3)= – 2.25V I (3)= – 3A 叠加 I=I(1)+I(2)+I(3)= 0.5+1–3= – 1.5A U=U(1)+U(2)+U(3)= 0+1.5–2.25= – 0.75V P3= = = 0.19W U2 3 3 –0.752 P3 U + + = 2.44W (1)2 3 U(2)2 3 U(3)2 3
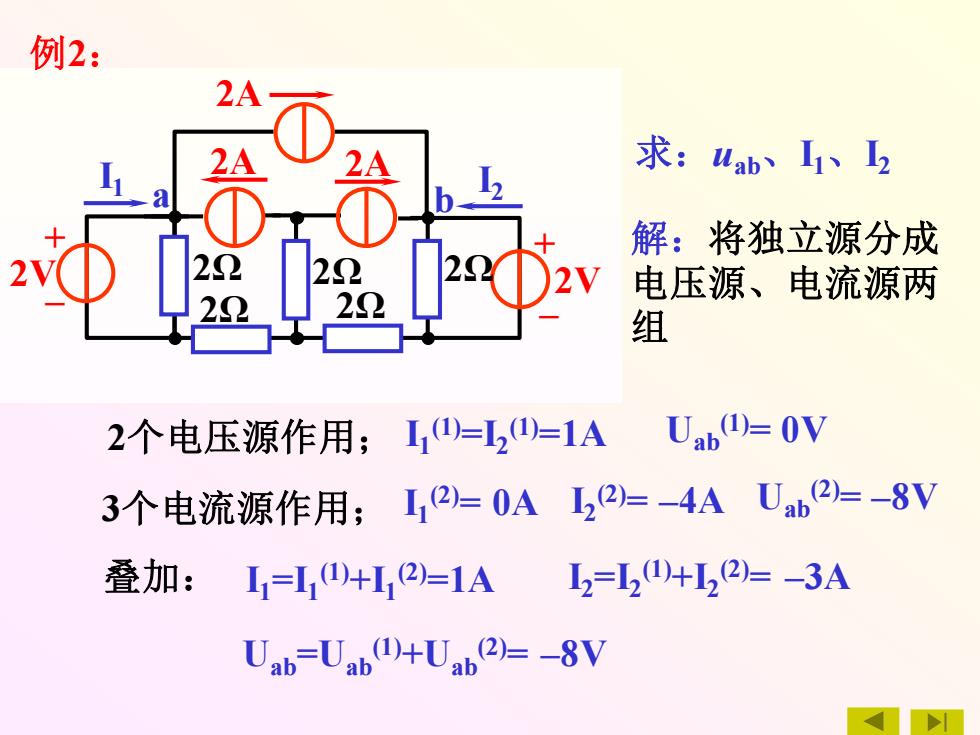
例2: 2A 2A 求:Wab2 解:将独立源分成 2( 电压源、电流源两 29 组 2个电压源作用;==1A Uab()=OV 3个电流源作用;12=0A22)=-4AUab2=-8V 叠加:11=0+H,2=1A220+L22=-3A Uab=Uab0)+Uab@2)=-8V
+ – + – a b I1 2V 2V 2A 2A 2A I2 2Ω 2Ω 2Ω 2Ω 2Ω 求:uab、I1、I2 I1 (1)=I2 (1)=1A Uab (1)= 0V I1 (1) I2 (1) + – + – a b I1 2V 2V 2A 2A 2A I2 2Ω 2Ω2Ω 2Ω 2Ω I2 (2) I1 (2) 2个电压源作用; 解:将独立源分成 电压源、电流源两 组 3个电流源作用; I1 (2)= 0A I2 (2)= –4A Uab (2)= –8V 叠加: I1=I1 (1)+I1 (2)=1A I2=I2 (1)+I2 (2)= –3A Uab=Uab (1)+Uab (2)= –8V + – + – a b I1 2V 2V 2A 2A 2A I2 2Ω 2Ω 2Ω 2Ω 2Ω 例2:
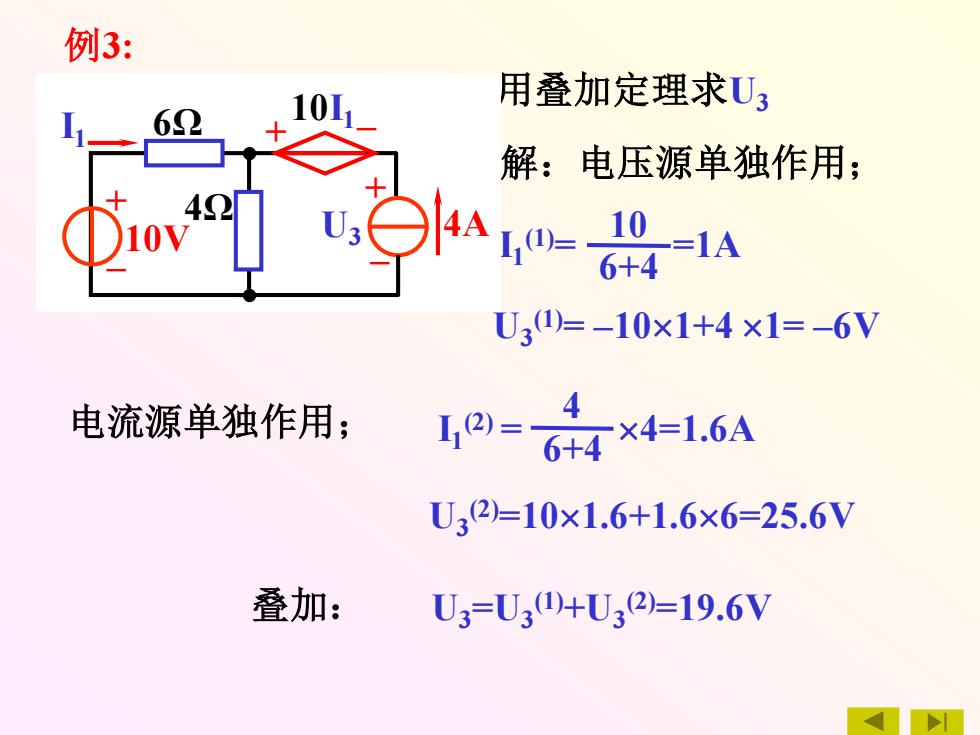
例3: 用叠加定理求U3 解:电压源单独作用; 42 4A=10 6+4 U30=-10×1+4×1=-6V 电流源单独作用; 12)=4 4×4=1.6A U32=10×1.6+1.6×6=25.6V 叠加: U3=U30+U32)=19.6V
+ – + – 10V 6Ω – + I1 10I1 U3 4A 4Ω 用叠加定理求U3 解:电压源单独作用; + – + – 10V 6Ω – + I1 (1) 10I1 (1) U3 4Ω (1) I1 (1)= =1A 6+4 10 U3 (1)= –101+4 1= –6V + – + – 10V 6Ω – + I1 10I1 U3 4A 4Ω 电流源单独作用; – + 10V 6Ω – + I1 (2) 10I1 (2) U3 (2) 4A 4Ω 6+4 4 I1 (2) = 4=1.6A + – + – 10V 6Ω – + I1 10I1 U3 4A 4Ω 例3: U3 (2)=101.6+1.66=25.6V 叠加: U3=U3 (1)+U3 (2)=19.6V