
飞号与事我 §1,5信号的分解 *¥ 新疆大学信息科学与工程学院电子系 2011.1 退出 开始
新疆大学信息科学与工程学院电子系 2011.1 §1.5 信号的分解

序言 为了便于研究信号的传输和处理问题,往往将信 号分解为一些简单(基本)的信号之和,分解角度不 同,可以分解为不同的分量 直流分量与交流分量 偶分量与奇分量 。 脉冲分量 实部分量与虚部分量 正交函数分量 利用分形理论描述信号
X 第 2 序言 页 为了便于研究信号的传输和处理问题,往往将信 号分解为一些简单(基本)的信号之和,分解角度不 同,可以分解为不同的分量 • 直流分量与交流分量 • 偶分量与奇分量 • 脉冲分量 • 实部分量与虚部分量 • 正交函数分量 • 利用分形理论描述信号
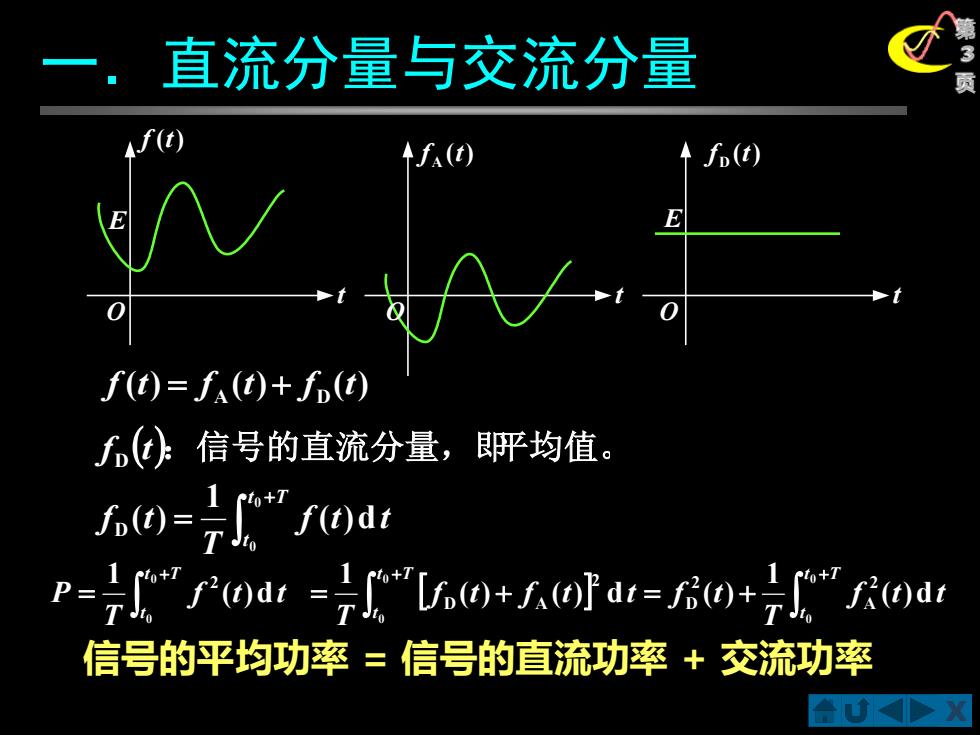
直流分量与交流分量 个f() (t) f(t)=f()+f(t) f)信号的直流分量,目 评均值。 0=0a P=”r0d:=0+rod=0+”0a 信号的平均功率=信号的直流功率+交流功率
X 第 3 一.直流分量与交流分量 页 ( ) ( ) ( ) A D f t = f t + f t f D (t):信号的直流分量,即平均值。 + = t T t f t t T f t 0 0 ( )d 1 ( ) D 信号的平均功率 = 信号的直流功率 + 交流功率 f (t) E E O t t t ( ) A f t ( ) D f t O O f t t T f t f t t f t T f t t T P t T t t T t t T t ( )d 1 ( ) ( ) d ( ) 1 ( )d 1 0 0 0 0 0 0 2 A 2 D 2 D A 2 + + + = = + = +

偶分量与奇分量 对任何实信号而言: f0=j0+J,.e体奇分量 f()少:偶分量 d)=() e:even fd)=-f(t)o:odd f0=,f④+f-】 1.国=/0- 信号的平均功率=偶分量功率+奇分量功率 侧题
X 第 4 二.偶分量与奇分量 页 对任何实信号而言: 信号的平均功率 = 偶分量功率 + 奇分量功率 ( ) ( ) e : even ( ) ( ) o : odd ( ): ( ): ( ) ( ) ( ) e e o o o e e o f t f t f t f t f t f t f t f t f t = − = − − = + 奇分量 偶分量 ( ) ( ) 2 1 ( ) e f t = f t + f −t ( ) ( ) 2 1 ( ) o f t = f t − f −t

三.脉冲分量 1.矩形窄脉冲序列 tr(t) 当t=t, 脉高:f(z),脉宽:△x,存在区间:u(t-x)-u(t-x-△x) 此窄脉冲可表示为 f(c儿at-x)-(t-x-△x)] 合UD
X 第 5 页 f (t) t f ( ) O 三.脉冲分量 当t = , 脉高:f ( ), 脉宽: , 1.矩形窄脉冲序列 此窄脉冲可表示为 f ( )u(t − )− u(t − − ) 存在区间:u(t − )− u(t − − )

从x=-o到o,f(t)可表示为许多窄脉冲叠加 f0=∑fc)lu(t-)-at-t-△x小] -00 -2fa,lt-yg-A】ag △T 令△x→0 lim Mu(t-)-ut-F-AD]dt-=8(t-) △→0 △T dt r→d,∑→ 出现在不同时刻的, TE- 不同强度的冲激函 所以f(0=f(e)(t-)dr 数的和
X 第 6 页 出现在不同时刻的, 不同强度的冲激函 数的和。 从 = − 到, f (t)可表示为许多窄脉冲的叠加 − − − − = =− u t u t ) f ( ) ( ( ) =− = − − − − f (t) f ( ) u(t ) u(t ) − 所以 f (t) = f ( ) (t − )d 令 → 0 ( ) = − − = − − − − → t t u t u t u t d ( ) ( d ( ) lim 0 ) =− =− → → d

2.连续阶跃信号之和 tr() f(6) f(1- f(o f0=J0u0+rag-4 dt 将信号分解为冲激信号叠加的方法应用很广 后面的卷积积分中将用到,可利用卷积积分求系统 的零状态响应
X 第 7 页 2.连续阶跃信号之和 = + − 0 1 1 1 1 ( )d d d ( ) ( ) (0) ( ) u t t t t f t f t f u t 将信号分解为冲激信号叠加的方法应用很广, 后面的卷积积分中将用到,可利用卷积积分求系统 的零状态响应。 f (t) 1 t 1 t t f (0) ( ) 1 1 f t − t ( ) 1 f t O

四.实部分量与虚部分量 瞬时值为复数的信号可分解为实虚部两部分之和。 f(t)=f(t)+(t) 共轭复函数 f()=f.()-if() 即 mo-fr+rl ino-fro-Fl 实际中产生的信号为实信号,可以借助于复信号来研 究实信号
X 第 8 四.实部分量与虚部分量 页 瞬时值为复数的信号可分解为实虚部两部分之和。 即 实际中产生的信号为实信号,可以借助于复信号来研 究实信号。 共轭复函数 ( ) ( ) j ( ) r i f t = f t + f t ( ) ( ) j ( ) r i * f t = f t − f t ( ) ( ) 2 1 ( ) * r f t = f t + f t ( ) ( ) 2 1 j ( ) * i f t = f t − f t

五.正交函数分量 如果用正交函数集来表示一个信号,那么,组成信 号的各分量就是相互正交的。把信号分解为正交函数分 量的研究方法在信号与系统理论中占有重要地位,这将 是本课程讨论的主要课题。 我们将在第三章中开始学习
X 第 9 五.正交函数分量 页 如果用正交函数集来表示一个信号,那么,组成信 号的各分量就是相互正交的。把信号分解为正交函数分 量的研究方法在信号与系统理论中占有重要地位,这将 是本课程讨论的主要课题。 我们将在第三章中开始学习

六.利用分形 (fractal) 理论描述信譬 分形几何理论简称分形理论或分数维理论: 创始人为B.B.Mandelbrot; 示例 分形是“其部分与整体有形似性的体系”; 在信号传输与处理领域应用分形技术的实例表现在 以下几个方面:图像数据压缩、语音合成、地震信 号或石油探井信号分析、声纳或雷达信号检测、通 信网业务流量描述等。这些信号的共同特点都是具 有一定的自相似性,借助分性理论可提取信号特征 并利用一定的数学迭代方法大大简化信号的描述 或自动生成某些具有自相似特征的信号。 可浏览网站:htp:/www.fractal.com
X 第 10 六.利用分形( 页 fractal)理论描述信号 • 分形几何理论简称分形理论或分数维理论; • 创始人为B.B.Mandelbrot; • 分形是“其部分与整体有形似性的体系”; • 在信号传输与处理领域应用分形技术的实例表现在 以下几个方面:图像数据压缩、语音合成、地震信 号或石油探井信号分析、声纳或雷达信号检测、通 信网业务流量描述等。这些信号的共同特点都是具 有一定的自相似性,借助分性理论可提取信号特征, 并利用一定的数学迭代方法大大简化信号的描述, 或自动生成某些具有自相似特征的信号。 可浏览网站:http://www.fractal.com 示例