
心号与素婴 §27卷积的性质 代数性质 •微分积分性质 与冲激函数或阶跃函数的卷积 新疆大学信息科学与工程学院电子系 2011.1 退出 开始
新疆大学信息科学与工程学院电子系 2011.1 §2.7 卷积的性质 •代数性质 •微分积分性质 •与冲激函数或阶跃函数的卷积

代数性质 1.交换律 f()*f2()=f2()*f) 证明 2.分配律 f(t)*[f(t)+f3(t)川=f(t)*f2()+f(t)*f3() 系统并联运算 3.结合律 [f()*f(]*f,(0=f()*[f()*方,()】 系统级联运算
X 第 2 一.代数性质 页 1.交换律 2.分配律 3.结合律 ( ) ( ) ( ) ( ) 1 2 2 1 f t f t = f t f t ( ) [ ( ) ( )] ( ) ( ) ( ) ( ) 1 2 3 1 2 1 3 f t f t + f t = f t f t + f t f t ( ) ( ) ( ) ( ) [ ( ) ( )] 1 2 1 2 f t f t f t = f t f t f t 系统并联运算 系统级联运算
系统并联 f1(t)*[f2(t)+f3(】=f1(t)*f2()+f1(t)*f3(t) 系统并联,框图表示: h(t) h(t) f(t)*h(t) f(t) 8(t) f(t)*h(t)+f(t)*h(t) f(t) h2(t) =f(t)*h(t) f(t)*h2(t) f(t h(t) 8@)=,d)+h,(d) 结论:子系统并联时,总系统的冲激响应等于 各子系统冲激响应之和
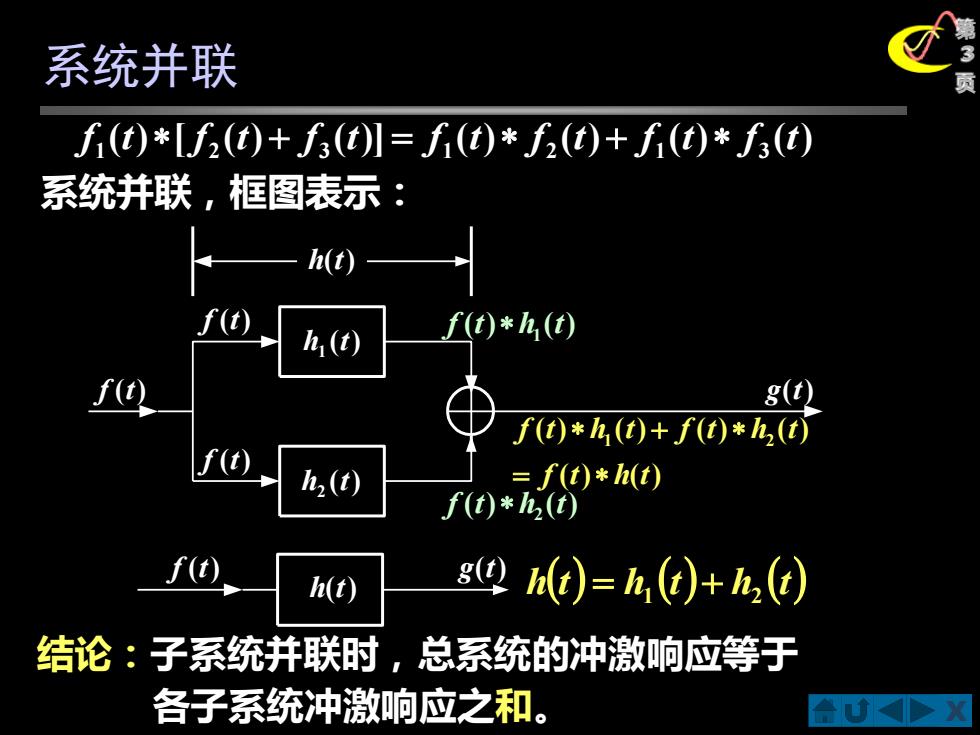
X 第 3 系统并联 页 h(t) h (t) h (t) = 1 + 2 ( ) [ ( ) ( )] ( ) ( ) ( ) ( ) 1 2 3 1 2 1 3 f t f t + f t = f t f t + f t f t 系统并联,框图表示: f (t) g(t) h(t) g(t) f (t) f (t) f (t) h(t) ( ) 1 h t ( ) 2 h t ( ) ( ) 1 f t h t ( ) ( ) 2 f t h t ( ) ( ) ( ) ( ) ( ) ( ) 1 2 f t h t f t h t f t h t = + 结论:子系统并联时,总系统的冲激响应等于 各子系统冲激响应之和

系统级联 f()*h()*h()=f(t)*[h,(t)*h(t】=f(t)*h(t) 系统级联,框图表示: h(t) h,(t) g(t) f(t)*h (t) f(t)*h,(t)*h2(t) h(t) g( t)=h()*h,(t) 结论:时域中,子系统级联时,总的冲激响应等 于子系统冲激响应的卷积
X 第 4 系统级联 页 ( ) ( ) ( ) ( ) [ ( ) ( )] 1 2 1 2 f t h t h t = f t h t h t = f (t) h(t) ( ) ( ) ( ) 1 2 h t = h t h t 系统级联,框图表示: f (t) ( ) 1 h t ( ) 2 h t g(t) ( ) ( ) 1 f t h t ( ) ( ) ( ) 1 2 f t h t h t f (t) g(t) h(t) 结论:时域中,子系统级联时,总的冲激响应等 于子系统冲激响应的卷积

二.微分积分性质 g'()=f(t)*hN(t)=f'(t)*h(t) 证明 推广: g(0的积分 g()=f(t)*h-()=f-()*(0 g()=f()*n0()=f()*(t) 微分性质积分性质联合实用 g"-(0=f(0*h-m()=fm()*0() 微分n次, 积分m次 作n,微分次数= g(t)=fm(t)*hm(t)) 积分次数 对于卷积很方便
X 第 5 二.微分积分性质 页 g(t) = f (t)h(t) = f (t)h(t) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) g t f t h t f t h t n m n m m n = = − − − ( ) ( ) ( ) ( ) ( ) g t f t h t n −n = ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) g t f t h t f t h t n n n = = 推广: 微分性质积分性质联合实用 ( ) ( ) ( ) ( ) ( ) ( 1) ( 1) ( 1) g t = f t h t = f t h t − − − 对于卷积很方便。 g(t)的积分 微分n次, 积分m次 m=n, 微分次数= 积分次数

三.与冲激函数或阶跃函数的卷积 ()6()=-)=-)5()dr=f() 推广: of(t)*8(t-to)=f(t-to) o f(t-ti)*8(t-t2)=f(t-t-t2) ●f()*δ'()=f"(t) ·f0*0=∫fadz 侧题 ●f(0)*δ(0)=f() ●f0*δt-t0)=fNt-o) 侧题 合UD
X 第 6 三.与冲激函数或阶跃函数的卷积 页 推广: f (t − t1) (t − t 2) = f (t − t1 − t 2) f (t) (t) = f '(t) ( ) ( ) ()d − = t f t u t f ( ) ( ) f (t) (t) f (t) k k = f (t) (t − t 0) = f (t − t 0) f (t) (t) = f ( ) (t − ) = f (t − ) ( ) = f (t) − − d d ( ) ( ) f (t) (t t 0) f (t t 0) k k − = −