
心号与系我 §24零输入响立和零状态响应 起始状态与激励源的等效转换 ·系统响应划分 •对系统线性的进一步认识 新疆大学信息科学与工程学院电子系 2011.1 退出 开始
新疆大学信息科学与工程学院电子系 2011.1 §2.4 零输入响应和零状态响应 •起始状态与激励源的等效转换 •系统响应划分 •对系统线性的进一步认识
起始状态与激励源的等效转挺: 在一定条件下,激励源与起始状态之间可以等效转换。 即可以将原始储能看作是激励源。 电容的等效电路 电感的等效电路 外加激励源 系统的完全响应 共同作用的结果 可以看作 起始状态等效激励滹 系统的完全响应= 零输入响应+ 零状态响应 (线性系统具有叠加性
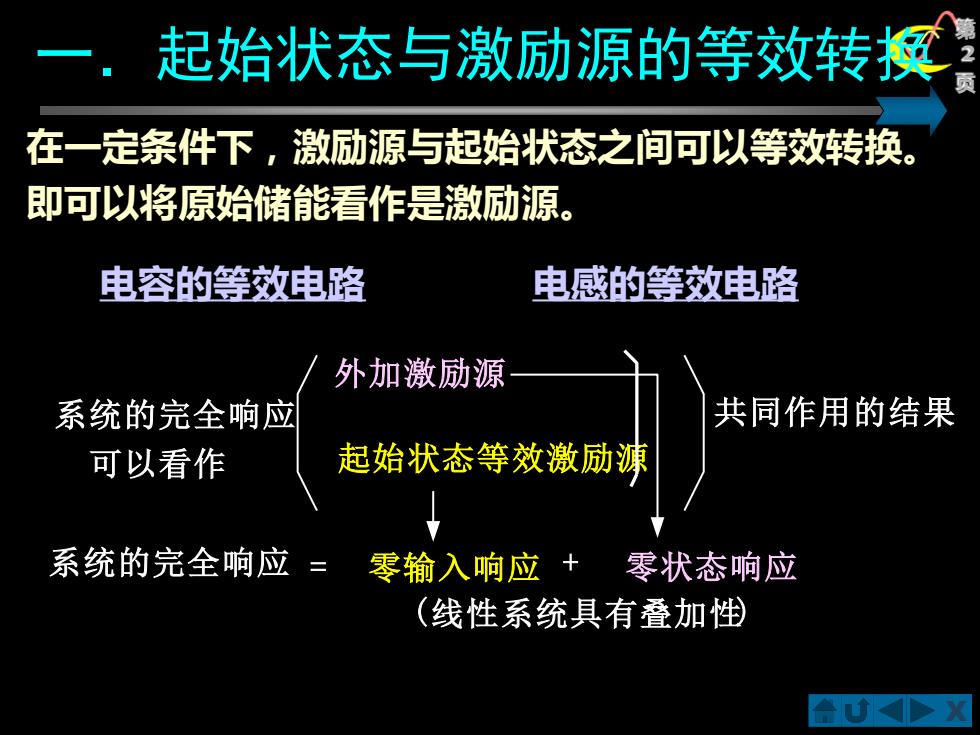
X 第 2 一.起始状态与激励源的等效转换 页 在一定条件下,激励源与起始状态之间可以等效转换。 即可以将原始储能看作是激励源。 电容的等效电路 电感的等效电路 外加激励源 系统的完全响应 共同作用的结果 可以看作 起始状态等效激励源 系统的完全响应 = 零输入响应 + 零状态响应 (线性系统具有叠加性)

电容器的等效电路 vc(0)≠0,t≥0 vc(t) ve()-cLd-ic(dr+idr =0)+e(a)dr t≥0 电路等效为起始状态为零的电容与电压源'c(0)4(的 串联 c0- e() 等效电路中的 电容器的起始 vc(t) 状态为零
X 第 3 电容器的等效电路 页 − = t C C i C v t ( )d 1 ( ) − − = + − t C C i C i C 0 0 ( )d 1 ( )d 1 − = − + t C C i t C v 0 ( )d 0 1 (0 ) C + vC (t) − i (t) C vC (0− ) 0,t 0 电路等效为起始状态为零的电容与电压源 的 串联 v u(t) C (0 ) − 等效电路中的 电容器的起始 状态为零 C + v (t) C i (t) C − vC(0−)

电感的等效电路 i,(t) iz(0_)≠0,t≥0 VL(t) 国=2.edr=g)dr+2a)a: =,0)+z(e)dxu20 故电路等效为起始状态为零的电感L和电流源,(0_)w(t) 的并联。 v.(t) L (E) iz(0-
X 第 4 页 − = t L L v L i t ( )d 1 ( ) − − = + − t L L v L v L 0 0 ( )d 1 ( )d 1 i (t) L + v (t) − L L ( )d ( 0) 1 (0 ) 0 = + − − v t L i t L L 故电路等效为起始状态为零的电感L和电流源 的并联。 i (0 )u(t) L − 电感的等效电路 i L (0− ) 0, t 0 i (t) L + − v (t) L L (0 − ) L i

二. 系统响应划分 自由响应+强迫响应 (Natural+forced) 暂态响应+稳态响应 (Transient+Steady-state) 零输入响应+零状态响应 (Zero-input+Zero-state)
X 第 5 二.系统响应划分 页 自由响应+强迫响应 (Natural+forced) 零输入响应+零状态响应 (Zero-input+Zero-state) 暂态响应+稳态响应 (Transient+Steady-state)

各种系统响应定义 (1)自由响称固有响应,由系统本身特性决定,与外加 激励形式无关。对应于齐次解。 强迫响应:形式取决于外加激励。对应于特解。 (2)暂态响应:是指激励信号接入一段时间内,完全响应中 暂时出现的有关成分,随着时间增加,它将消失。 稳态响应:由完全响应中减去暂态响应分量即得稳态 响应分量。 (3)零输入瘦海外加激励信号的作用,只由起始状态(起 始时刻系统储能)所产生的响应。 零状态趣滤原始时刻系统储能的作用(起始状态等 于零),由系统的外加激励信号产生的响应
X 第 6 页 也称固有响应,由系统本身特性决定,与外加 激励形式无关。对应于齐次解。 形式取决于外加激励。对应于特解。 是指激励信号接入一段时间内,完全响应中 暂时出现的有关成分,随着时间t 增加,它将消失。 由完全响应中减去暂态响应分量即得稳态 响应分量。 没有外加激励信号的作用,只由起始状态(起 始时刻系统储能)所产生的响应。 不考虑原始时刻系统储能的作用(起始状态等 于零),由系统的外加激励信号产生的响应。 (1)自由响应: (2)暂态响应: 稳态响应: 强迫响应: (3)零输入响应: 零状态响应: 各种系统响应定义

求解 系统零输入响应,实际上是求系统方程的齐次解,由 非零的系统状态值 yc0_决的初始值求出待定系数。 系统零状态响应,是在激励作用下求系统方程的非齐沙 解,由状态值v(0树决定的初始值求出待定系数。 求解非齐次微分方程是比较烦琐的工作,所以引出卷积 积分法。 线性时不变系统 nt) 系统的零状态响应=激励与系统冲激响应的卷积,即 r(t)=e(t)*h(t)
X 第 7 页 系统零输入响应,实际上是求系统方程的齐次解,由 非零的系统状态值 ( ) 决定的初始值求出待定系数。 ( ) C 0− L 0− v 和 i 系统零状态响应,是在激励作用下求系统方程的非齐次 解,由状态值 ( ) 为零决定的初始值求出待定系数。 ( ) C 0− L 0− v 和 i 求解非齐次微分方程是比较烦琐的工作,所以引出卷积 积分法。 (t) 线性时不变系统 h(t) e(t) h(t) r(t) 求解 系统的零状态响应=激励与系统冲激响应的卷积,即 r(t) = e(t) h(t)

三.对系统线性的进一步认识 由常系数微分方程描述的系统在下述意义上是线性的。 (1)响应可分解为:零输入响应+零状态响应。 (②)零状态线性:当起始状态为零时,系统的零状态响应 对于各激励信号呈线性。 (3)零输入线性:当激励为零时,系统的零输入响应对于 各起始状态呈线性。 侧题
X 第 8 三.对系统线性的进一步认识 页 由常系数微分方程描述的系统在下述意义上是线性的。 (1)响应可分解为:零输入响应+零状态响应。 (2)零状态线性:当起始状态为零时,系统的零状态响应 对于各激励信号呈线性。 (3)零输入线性:当激励为零时,系统的零输入响应对于 各起始状态呈线性