
狄利克雷(Dirichlet)条件 ☑ 条件1:在一周期内,如果有间断点存在,则间断点的 数目应是有限个。 侧题 条件2:在一周期内,极大值和极小值的数目应是有 限个。 创题 条件3:在一周期内,信号绝对可积。 说明 、创题 U
X 第 1 狄利克雷(Dirichlet)条件 页 条件3:在一周期内,信号绝对可积。 条件2:在一周期内,极大值和极小值的数目应是有 限个。 条件1:在一周期内,如果有间断点存在,则间断点的 数目应是有限个
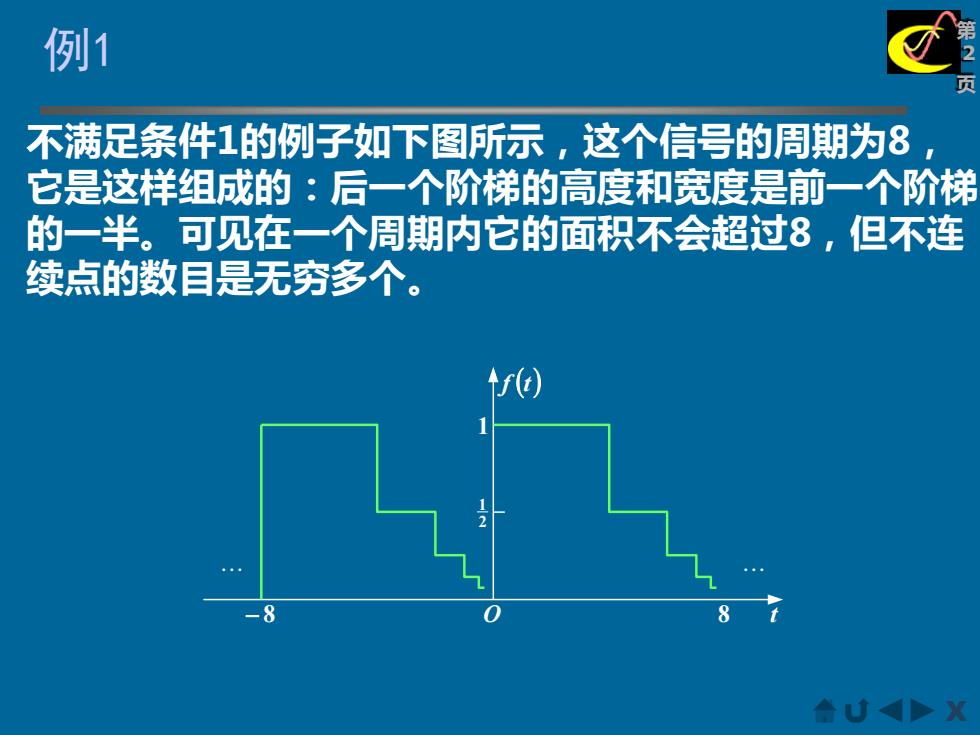
例1 不满足条件1的例子如下图所示,这个信号的周期为8 它是这样组成的:后一个阶梯的高度和宽度是前一个阶梯 的一半。可见在一个周期内它的面积不会超过8,但不连 续点的数目是无穷多个。 t) -8 8 合U4>
X 第 2 例 页 1 不满足条件1的例子如下图所示,这个信号的周期为8, 它是这样组成的:后一个阶梯的高度和宽度是前一个阶梯 的一半。可见在一个周期内它的面积不会超过8,但不连 续点的数目是无穷多个。 f (t) O 1 − 8 8 t 2 1
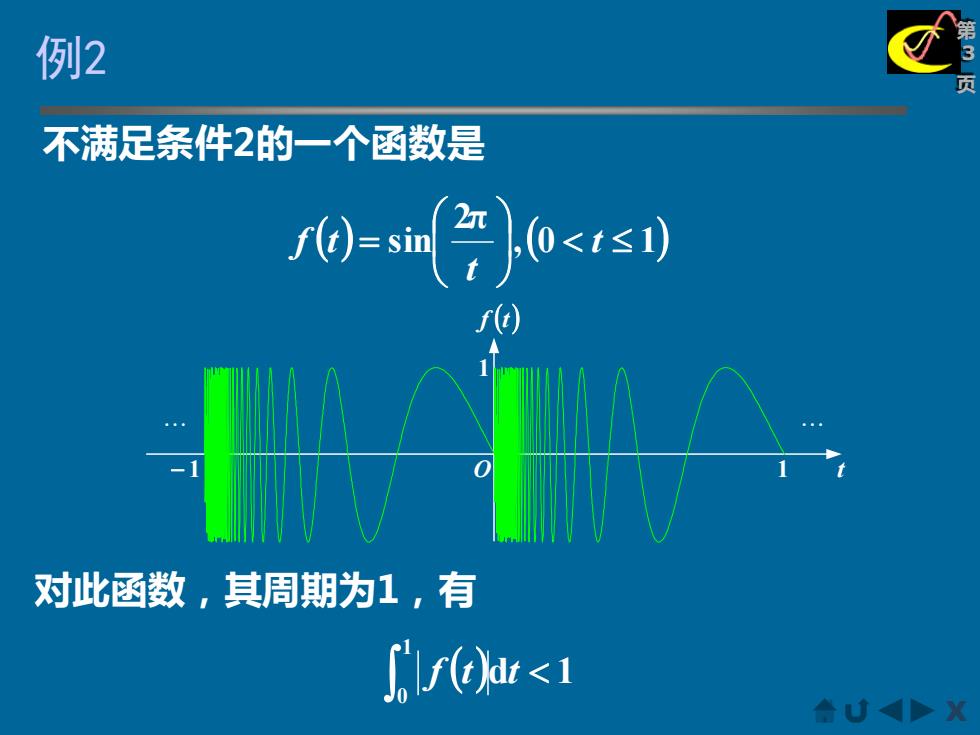
例2 不满足条件2的一个函数是 <s1) 对此函数,其周期为1,有 r<1 合U风
X 第 3 例 页 2 不满足条件2的一个函数是 ( ) ,(0 1) 2π sin = t t f t f (t) O 1 − 1 1 t 对此函数,其周期为1,有 ( )d 1 1 0 f t t

说明 在一周期内,信号是绝对可积的(T为周期) 与平方可积条件相同,这一条件保证了每一系数F都 是有限值,因为 =(d 1F<o←☐Jr0a<四
X 第 4 页 在一周期内,信号是绝对可积的(T1为周期) ( ) T f t t T d 1 0 + 1 0 ( ) d t T t f t t ( ) ( ) = T T n t n f t t T f t t T F d 1 e d 1 1 j 说明 与平方可积条件相同,这一条件保证了每一系数Fn都 是有限值,因为 Fn
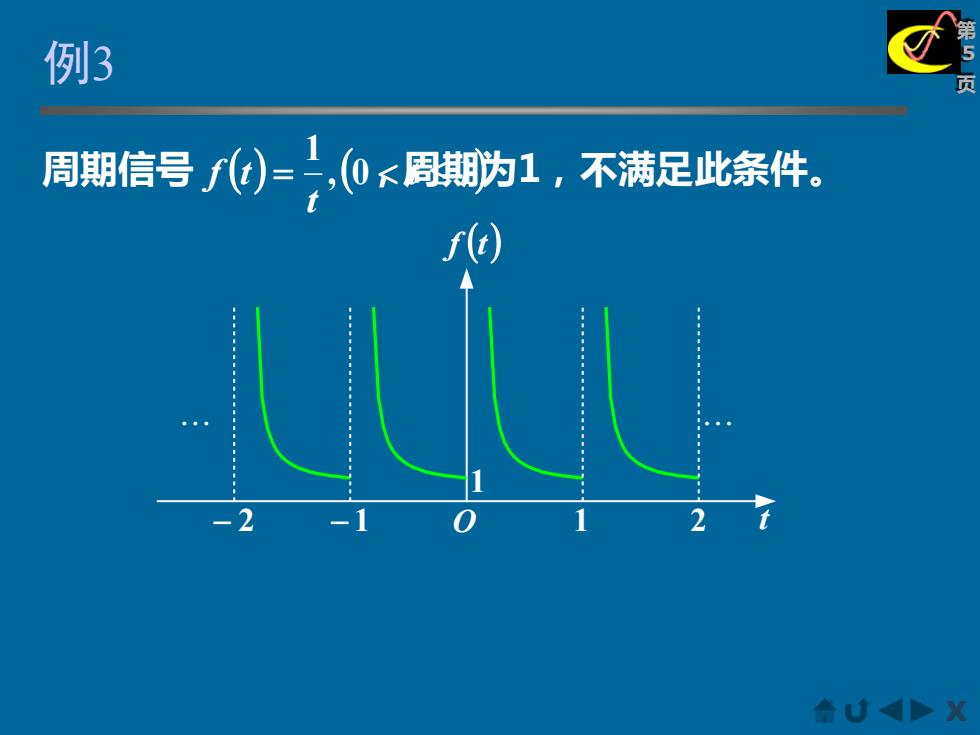
例3 周期信号f0=,(00
X 第 5 例3 页 周期信号 ( ) ,(0 ,周期为 1) 1,不满足此条件。 1 = t t f t f (t) O 1 − 2 − 1 1 2 t