例3-7-4(时移性质,教材3-2) 求图(a)所示三脉冲信号的 f 频谱。 解 令fd)表示矩形单脉冲 -2 (a)三脉冲信号的波形 信号,其频谱函数(o)》 F.(@) Et F (@)=Et-Sa @t 2 2n (b)
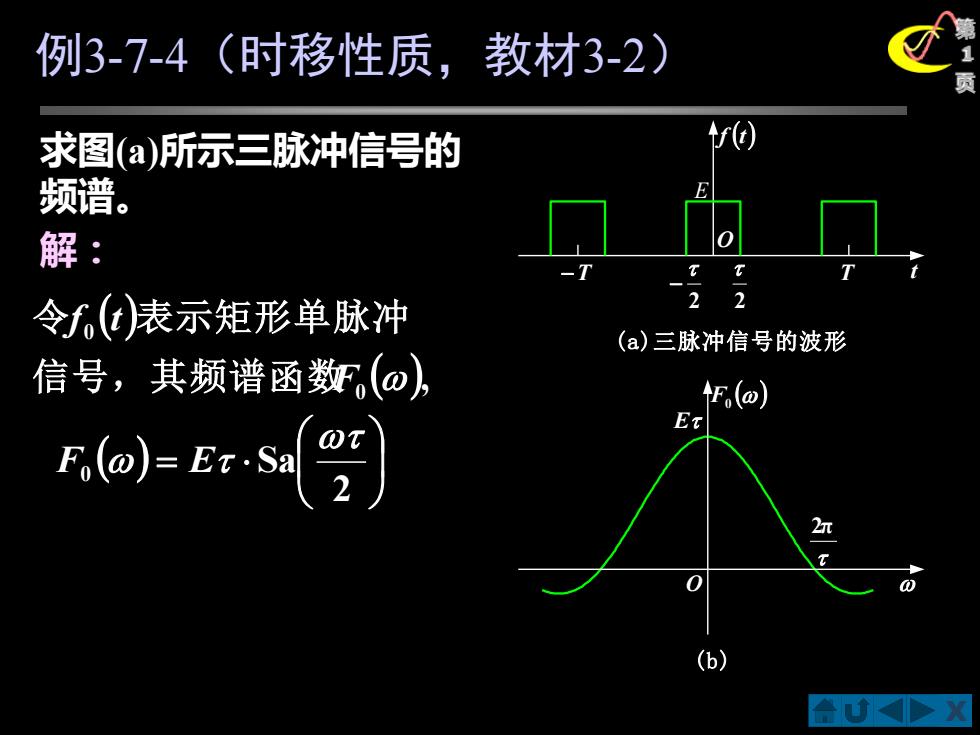
X 第 1 例 页 3-7-4(时移性质,教材3-2) 求图(a)所示三脉冲信号的 频谱。 f (t) t 2 2 − −T T E (a)三脉冲信号的波形 解: O ( ) ( ), 0 0 F f t 信号,其频谱函数 令 表示矩形单脉冲 ( ) = 2 0 Sa F E 2π () F0 E O (b)
因为 F(@) Et f)=fd)+f(t+T)+ft-T) 由时移性质知三脉冲数f(d) 的频谱函数F(o为: F(o)=F(ol+er+eir) =Ersg+2 mo】 脉冲个数增多,频谱 演示 T 包络不变,带宽不变。 (c)三脉冲信号的频谱
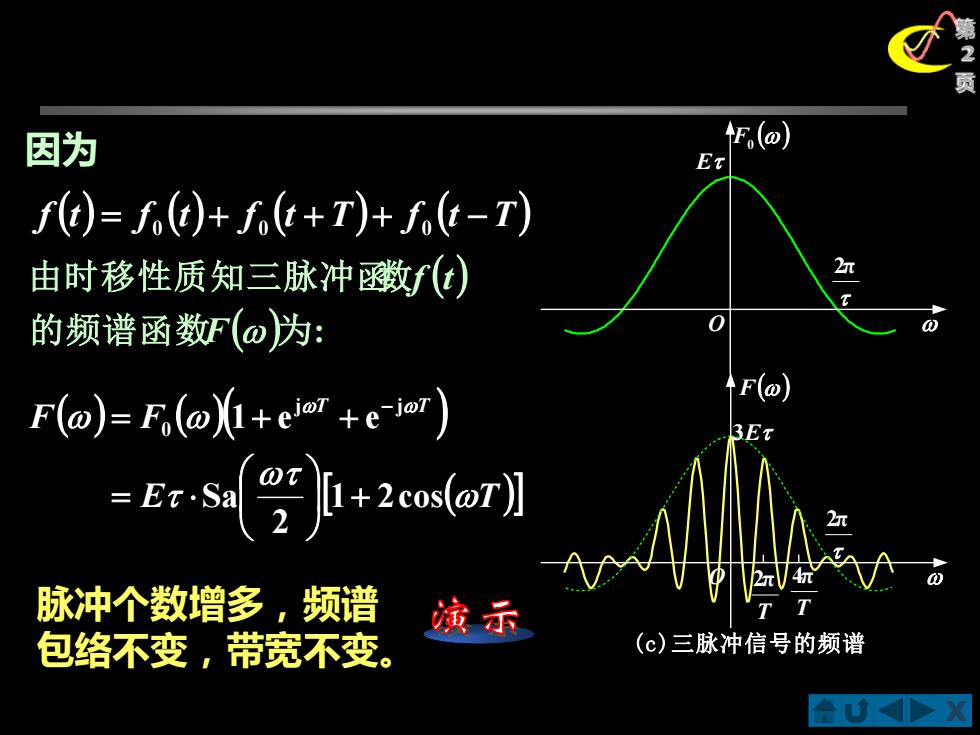
X 第 2 页 2π () F0 E O 因为 f (t) = f (t) + f (t + T) + f (t −T) 0 0 0 ( ) 的频谱函数 ( )为: 由时移性质知三脉冲函数 F f t ( ) ( )( ) E ( T) F F T T 1 2cos 2 Sa 1 e e j j 0 + = = + + − F() O T 2π 3E (c)三脉冲信号的频谱 T 4π 2π 脉冲个数增多,频谱 包络不变,带宽不变