《信号与系统》课程教学课件（PPT讲稿）§3.10 抽样信号的傅里叶变换

心号与系我 §3,10抽样信号的傅里叶变换 抽样 理想抽样 矩形脉冲抽样 并 新疆大学信息科学与工程学院电子系 2011.1 退出 开始

新疆大学信息科学与工程学院电子系 2011.1 §3.10 抽样信号的傅里叶变换 •抽样 •理想抽样 •矩形脉冲抽样

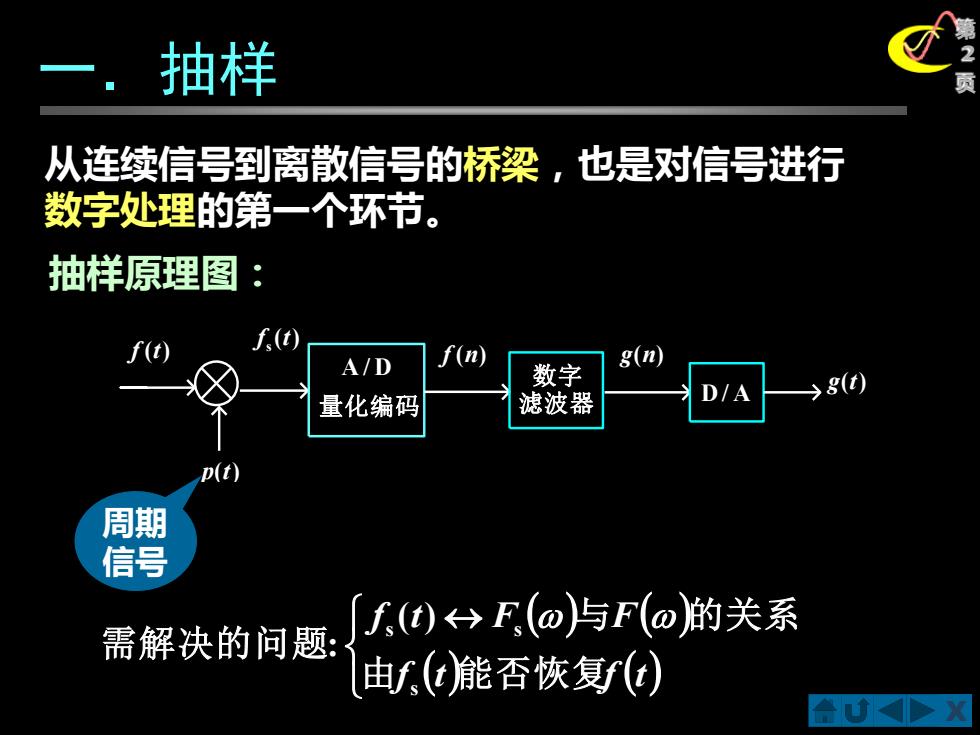
抽样 从连续信号到离散信号的桥梁，也是对信号进行 数字处理的第一个环节。 抽样原理图： A/D f(n) 数字 g(n D/A g(t) 量化编码 滤波器 D(t) 周期 信号 需解决的问题： [f0F(@)与F(@的关系 由f(t能否恢复f(t)

X 第 2 页 从连续信号到离散信号的桥梁，也是对信号进行 数字处理的第一个环节。 周期 信号 抽样原理图： 一．抽样 ( ) s f t A / D f (n) g(n) D/ A g(t) p(t) f (t) 量化编码 数 字 滤波器 ( ) ( ) ( ) ( )     f t f t f t F F 由 能否恢复 与 的关系 需解决的问题 s s s ( ) :  

理想抽样 (周期单位冲激抽 连续信号 抽样信号 fdFo）(←onP(@), 抽样脉冲 6-) sd@) p0=,0=∑t-nI)@,∑@-n@,) f(④=f0)6,(0=∑fnI,)5t-nI) F()-Fl().()-r(@)-5:(@)-;EF(-na.)

X 第 3 页    −  =−  ( ) = ( ) = ( − )  ( − )  T  nTs s   ns p t t t n 二．理想抽样（周期单位冲激抽样） 连续信号 抽样信号 抽样脉冲 f (t) f (t)  s (t)  T ( )  ( ) ( ) ( ) ( )  ( )  =−  = =  = − n F n T F F f t t F s s s T T 1 2π 1          =−  = = − n f (t) f (t) (t) f (nT ) (t nT ) s  T s  s ( ) ( ) ( )  F  − m   m f t p(t) P() , ( ) () s Fs f t 

2.冲激抽样信号的频谱 ) +F(o) 0 -000m 0 p(t ↑P(o) () 0 相 卷 乘 积 00m

X 第 4 页 t f(t) o t p(t) o TS E t f S (t) o TS o o o  F() P()  −s s ( ) s () Fs  s 1 T 1 − m  m −s  m s 相 乘 卷 积 (1)         2．冲激抽样信号的频谱

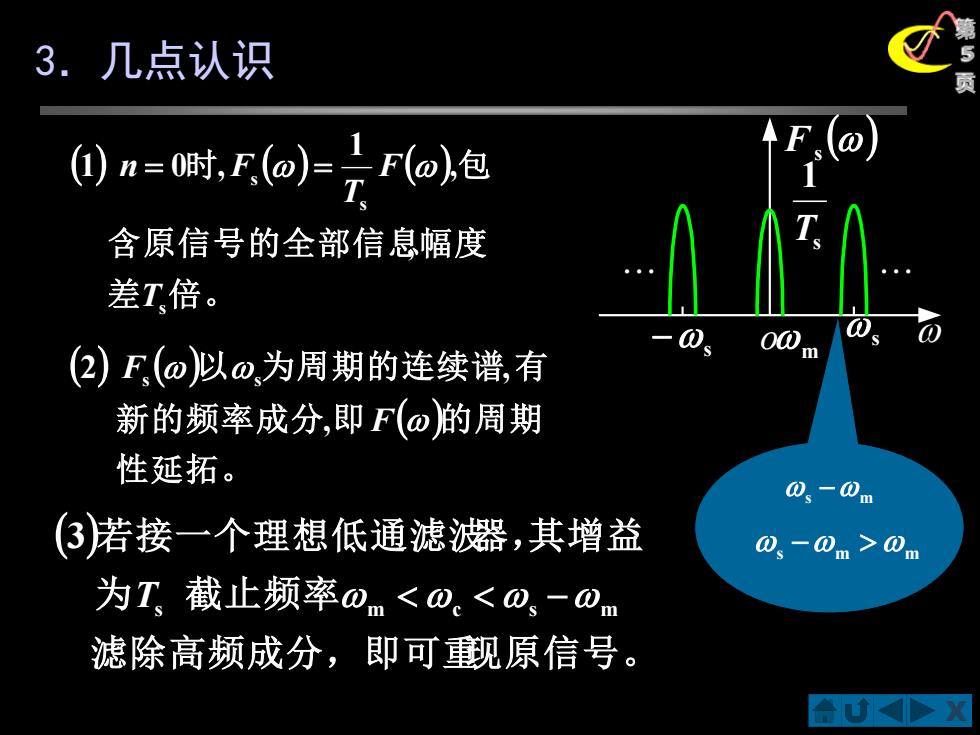
3.几点认识 n=0时F(o)=二Fo包 T 含原信号的全部信息幅度 差T倍。 一0s (2)F(@)以@，为周期的连续谱，有 00m 新的频率成分，即F(o的周期 性延拓。 0、-0m (③若接一个理想低通滤器，其增益 0-0m>0m 为T截止频率0m<0。<0-0nm 滤除高频成分，即可觐原信号

X 第 5 页 s − m s − m  m 3．几点认识 ( ) ( ) ( ) 差 倍 。 含原信号的全部信息幅 度 时 包 s s s , , 1 1 0 , T F T n = F  =  ( ) ( ) ( ) 性延拓。 新的频率成分 即 的周期 以 为周期的连续谱 有    F F , 2 , s s o () Fs  s 1 T  m s −s   ( ) 滤除高频成分，即可重现原信号。 为 截止频率 若接一个理想低通滤波器 ，其增益 3 Ts  m  c  s − m

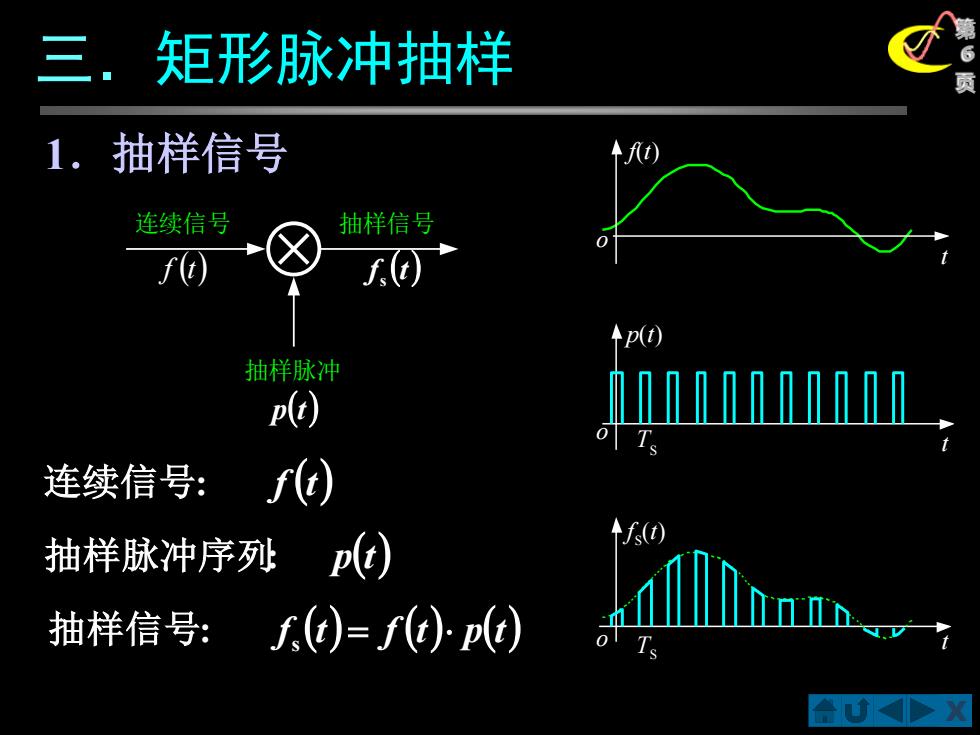
三.矩形脉冲抽样 1. 抽样信号 连续信号 抽样信号 个pt 抽样脉冲 ( 连续信号：ft) p(t) f(t) 抽样脉冲序列 抽样信号： )=5 p(e)

X 第 6 页 1．抽样信号 三．矩形脉冲抽样 连续信号: f (t) 抽样脉冲序列: p(t) f (t) = f (t) p(t) s 抽样信号: t f(t) o t o p(t) TS o T t S f S (t) 连续信号 抽样信号 抽样脉冲 f (t) f (t)  s p(t)

关系 连续信号：fd ft)>F@) （-0m<0<0m) 抽样脉冲序列：p r)+P(o). 限带 信号 抽样信号：f(d) f()@) ()=()( Eo-aro小Pa) ●x越小，越能反映离散刻之值，从信号传输角度看 更关心(d中有无f的全部信息，必须考虑f,(d的频 谱结构

X第7 关系 页 连续信号 : f (t ); 抽样脉冲序列 ： p (t ) f (t ) s 抽样信号 : ( ) ( ) ( )  F  − m     m f t p (t )  P () , ( ) () s Fs f t  ( ) ( ) ( ) 谱结构。 更关心 中有无 的全部信息，必须考虑 的 频 越小，越能反映离散时刻之值，从信号传输角度看 f t f t f t s s • , f (t) = f (t) p(t) s 限带 信号 F () F () P () s =  2π1

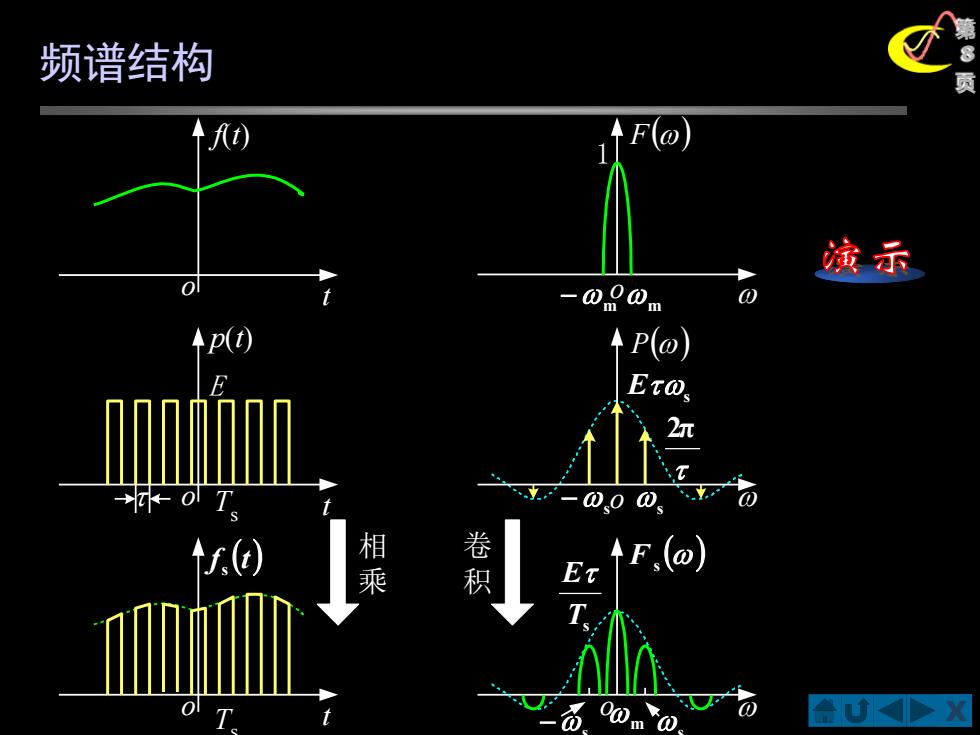
频谱结构 0) Fl@ 演示 p(t P(@) EtO 相乘 卷积 F(@)

X 第 8 页 t f(t) o t p(t)  o Ts E t o Ts o o o  F() P()   2π −s s s E  () Fs  Ts E 1 − m  m  m −s s 相 乘 卷 积 f (t) s 频谱结构

频谱结构的数学表示 F@)=FU0pt】=2元Fo*P@) p0Po)-=2n∑r.o-nm,) p电的腊系数R=7s not 2 P)is s(o-na.) Fo)-7立s”g}Foj-oo-a） nr-no)

X 第 9 频谱结构的数学表示 页 F () = Ff (t) p(t)= F() P() 2π 1 s ( ) ( )  ( )  =−   = − n p t P π Pn n s  2    ( )       = 2 Sa s s n  n  T p t 的谱系数P ( ) ( ) ( )  ( )   =−   =−   −      =   −      = n s s s n s s s s 2 Sa 2 Sa              F n n T F n n T F ( )  ( )  =−   −      = n n n T P s s s 2 2π Sa       

2. 举例说明抽样信号与原信号频谱的关察 因为ro-无之s”g）ro-a) 设： 会-。a所以年20月二次游泼为0 n=0E0=P回) n=1 5()n=1-aFo n=-1F.(o） F(o+ w+w 合心>

X 第 10 页 2．举例说明抽样信号与原信号频谱的关系 , π 2π π , 2 1 : s s s s = = =   =    T T 设 2 0 2π 所以 s即二次谐波为  = n = 0 n = 1 ( ) ( ) ( ) s s s π 1 2 π Sa 2 1 1    − =  −      = = F F n F n = −1 ( ) ( ) ( ) s s s π 1 π 2 2 1 1  =   + =  + = − F F n F ( )  ( )  =−   −      = n s s s s 2 Sa       F n n T 因 为 F F ( ) F() n 2 1 0 0 s = =