
心号与事裂 §4.6系统品数(网治盖数)牙S) 系统函数 LT互联网络的系统函数 并联级联 反馈连接 *头 新疆大学信息科学与工程学院电子系 2011.1 退出 开始
新疆大学信息科学与工程学院电子系 2011.1 §4.6 系统函数(网络函数)H(s) •系统函数 •LTI互联网络的系统函数 并联 级联 反馈连接
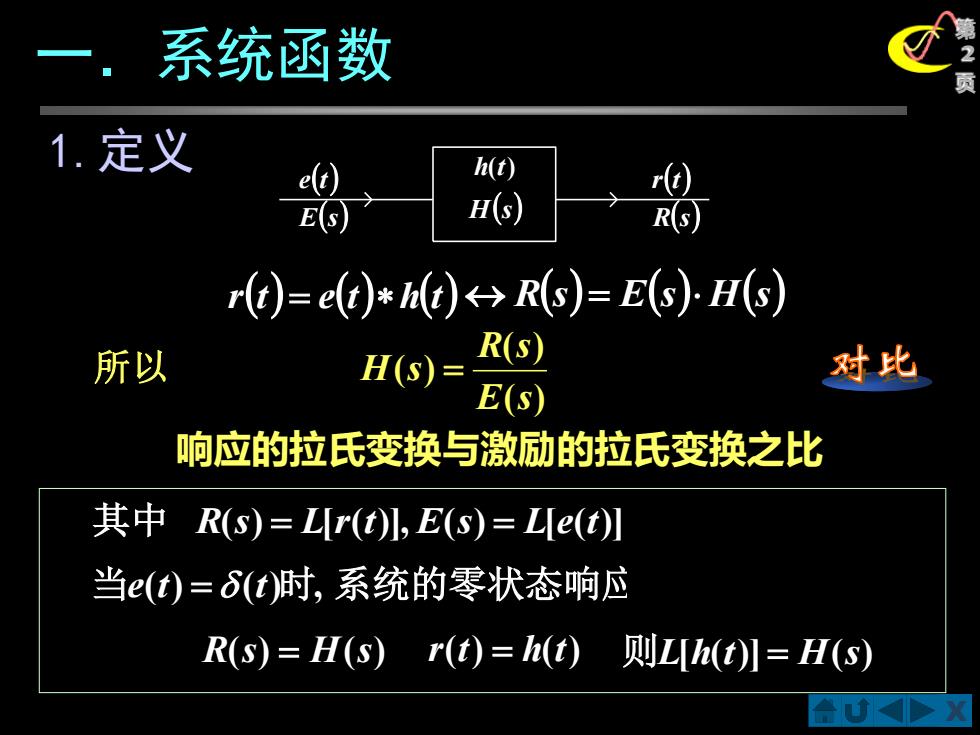
系统函数 1.定义 e() h(t) 园 E5 H(s) R(s) r)=ed)*d→R)=E(s)H(s 所以 R(s) 对比 E(s) 响应的拉氏变换与激励的拉氏变换之比 其中R(s)=L[r(t),E(s)=LIe(t 当(t)=6(t)时,系统的零状态响 R(s)=H(s)r(t)=h(t) 则L[(t)】=H(s)
X 第 2 页 1.定义 一.系统函数 R(s) = E(s) H(s) 响应的拉氏变换与激励的拉氏变换之比 h(t) H(s) e(t) E(s) r(t) R(s) ( ) ( ) ( ) E s R s 所 以 H s = r(t) = e(t)h(t) 其中 R(s) = L[r(t)], E(s) = L[e(t)] 当e(t) = (t)时, 系统的零状态响应 R(s) = H(s) r(t) = h(t) 则L[h(t)] = H(s)
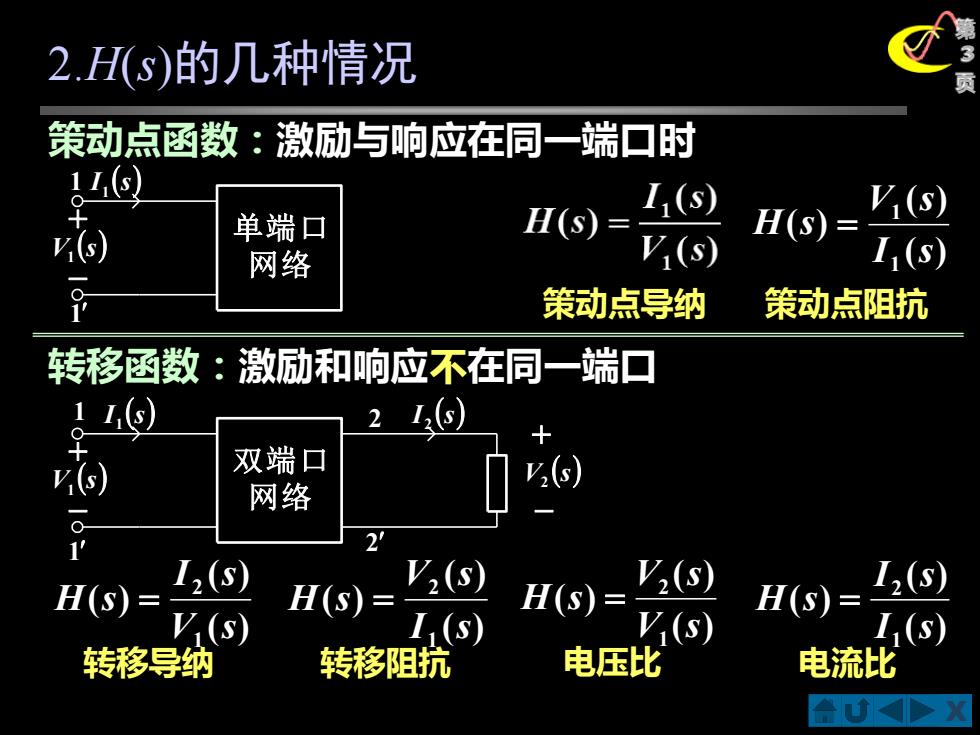
2.H(s)的几种情况 策动点函数:激励与响应在同一端口时 H(s)= I(s) 单端口 H(S)= V(s) ) 网络 V(s) I1(S) 策动点导纳 策动点阻抗 转移函数:激励和响应不在同一端口 2 16) y() 双端口 v(5) 网络 H(S)= 1(5) V (s) H(S)= V2(s) H(S)= V2(5) I (s) V (s) ( I2(s) (S) 转移导纳 转移阻抗 电压比 电流比
X 第 3 2.H 页 (s)的几种情况 策动点函数:激励与响应在同一端口时 策动点导纳 ( ) ( ) ( ) 1 1 I s V s H s = 策动点阻抗 单端口 网 络 I (s) 1 + − V (s) 1 1 1 双端口 网 络 I (s) 1 + − V (s) 1 1 1 I (s) 2 + − V (s) 2 2 2 ( ) ( ) ( ) 1 2 V s I s H s = 转移导纳 ( ) ( ) ( ) 1 2 I s V s H s = 转移阻抗 ( ) ( ) ( ) 1 2 V s V s H s = 电压比 ( ) ( ) ( ) 1 2 I s I s H s = 电流比 转移函数:激励和响应不在同一端口

3.求H(s)的方法 ●d)-→Hs) ·微分方程两端取拉氏变换H付)= E(s ·利用网络的域元件模型图,列域方程。6)- 侧题 4.应用:求系统的响应 ●方法一:H(s)→h(t)-→r(t)=e()*h(t) ·方法二:R(s)=H(S)E(S)→r(t) 例题
X 第 4 页 4.应用:求系统的响应 3.求H(s)的方法 方法一:H(s) → h(t) → r(t) = e(t)h(t) 方法二:R(s) = H(s)E(s) → r(t) h(t) → H(s) ( ) ( ) E(s) R s H s = ( ) ( ) E(s) R s 利用网络的s域元件模型图,列s域方程→ H s = 微分方程两端取拉氏变换→
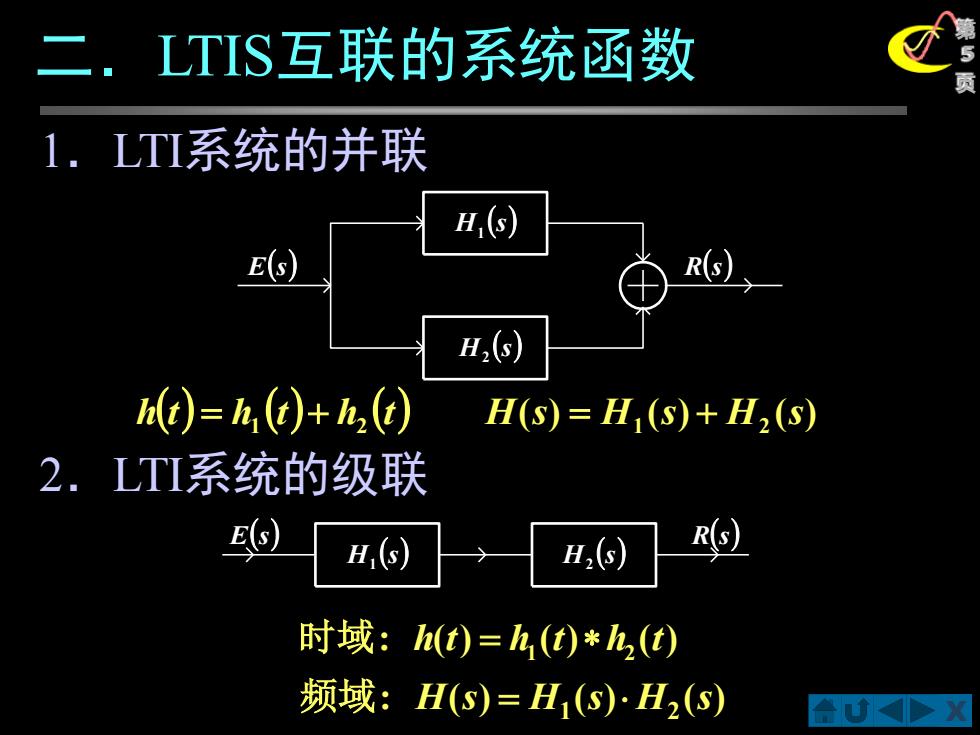
二.LTIS互联的系统函数 1.LTI系统的并联 H) E(s) R(G) (s) he)=h(t)+h) H(s)=H(S)+H2(S) 2.LTI系统的级联 E H,) H,6) R 时域:h(t)=h,(t)*h,(t) 频域:H(s)=H1(S)H2(s)
X 第 5 二.LTIS互联的系统函数 页 h(t) h (t) h (t) = 1 + 2 ( ) ( ) ( ) 1 2 H s = H s + H s : ( ) ( ) ( ) 1 2 时域 h t = h t h t : ( ) ( ) ( ) 1 2 频域 H s = H s H s H (s) 1 H (s) 2 E(s) R(s) H (s) 1 H (s) 2 E(s) R(s) 1.LTI系统的并联 2.LTI系统的级联
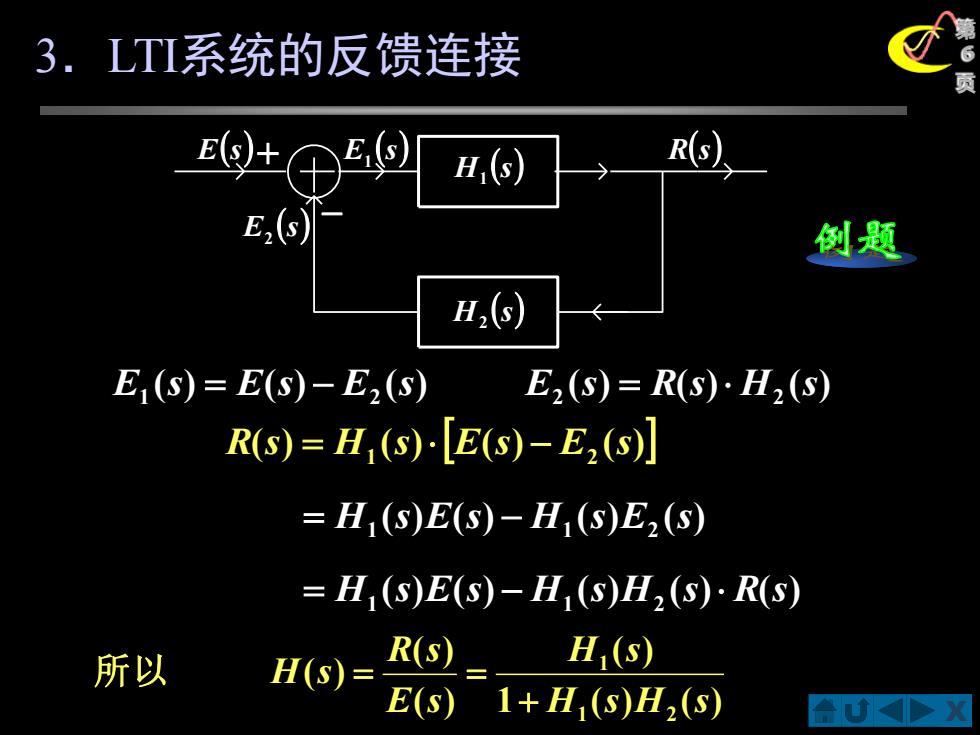
3.LTI系统的反馈连接 E(s)+ ES) H(s) R(s) E 侧题 H,s) E(S)=E(S)-E2(S) E2S)=R(s)·H2(s) R(s)=H1(s)·[E(s)-E2(s)] =H,(S)E(s)-H1(S)E2(S =H(s)E(s)-H(s)H2(s).R(s) 所以 H(S)=R()= H(s) E(s) 1+H1(S)H2(s) 合✉D
X 第 6 页 3.LTI系统的反馈连接 ( ) ( ) ( ) 1 2 E s = E s − E s ( ) ( ) ( ) 2 2 E s = R s H s ( ) ( ) ( ) ( ) 1 2 R s = H s E s − E s ( ) ( ) ( ) ( ) 1 1 2 = H s E s − H s E s ( ) ( ) ( ) ( ) ( ) 1 1 2 = H s E s − H s H s R s 1 ( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 H s H s H s E s R s H s + 所 以 = = H (s) 1 H (s) 2 E(s) E (s) R(s) 1 E (s) 2 − +

4. 结论 在s域可进行代数运算: ●已知子系统的,()或H,(s),可以求出整个系统的H(S) 已知总的H(s)及部分系统的H,(s),也可以求出另一个 子系统的H,(s)
X 第 7 4.结论 页 在s域可进行代数运算: 已知子系统的hi (t)或Hi (s),可以求出整个系统的 H(s)。 子系统的 。 已知总的 及部分系统的 ,也可以求出另一个 ( ) ( ) ( ) H s H s H s j i