
心号与系我 §5,4理想低通滤波器 ·理想低通的频率特性 理想低通的冲激响应 理想低通的阶跃响应 理想低通对矩形脉冲的响应 新疆大学信息科学与工程学院电子系 2003.1 退出 开始
新疆大学信息科学与工程学院电子系 2003.1 §5.4 理想低通滤波器 •理想低通的频率特性 •理想低通的冲激响应 •理想低通的阶跃响应 •理想低通对矩形脉冲的响应

理想低通的频率特性 忸Gw) p(o) -0.0 ⊙@. 即 >0 p(o)=-t 为截止频率,称为理想低通滤波器的通频带,简称频 带。 0在的低频段内,传输信号无失真( 只有时移
X 第 2 页 ( ) = − c c j 0 1 e j 0 t H 一.理想低通的频率特性 −c O c H(j) 1 ● 在0的低频段内 ~ c ,传输信号无失真 ( ) 。 0 只有时移t ● 为截止频率,称为理想低通滤波器的通频带,简称频 带。 c ( ) 0 = −t 即 ( ) = c c 0 1 j H O c −c ()

二. 理想低通的冲激响应 因为h(t)←→HGo) 所以0=F[Ho小-云oe"do 1eaw-k- 1 N、 eio(-h)0. g-g-】 会风
X 第 3 页 因为 h(t) H(j) − − = = (j )e d 2 1 ( ) (j ) 1 j t 所 以 h t F H H ( ) ( ) c c 0 c c 0 j 0 j ( ) e j 1 2π 1 1 e d 2π 1 − − − − − = = t t t t t t 二.理想低通的冲激响应 − − = c c t t 1 e e dω 2π 1 j j 0 ( ) ( ) ( ) c 0 c 0 j j 0 e e 2j 1 1 π 1 t t t t t t − − − − − = ( ) ( ) c 0 c c 0 sin π t t t t − − = ( ) c 0 c Sa π = t − t
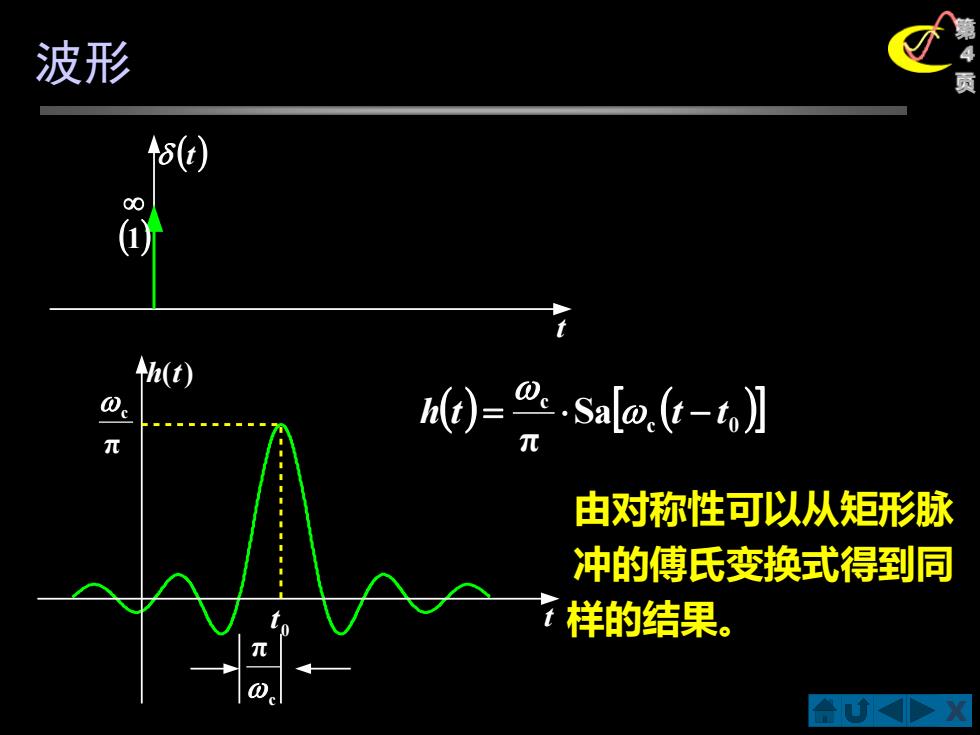
波形 5 00 (t) 0=gsao,t-,】 由对称性可以从矩形脉 冲的傅氏变换式得到同 t 样的结果
X 第 4 页 h(t) t 0 t c π π c ( ) ( ) c 0 c Sa π h t = t − t 波形 t (1) (t) 由对称性可以从矩形脉 冲的傅氏变换式得到同 样的结果

几点认识 1.比较输入输出,可见严重失真: 8d)→1信号频带无限宽, 而理想低通的通频带(系统频带)有限的 0~) 当过理想低通时,以止的频率成分都衰 减为0,所以失真。 当@。→o时,h(t)→6(t) 系统为全通网络,可以无失真传输。 2.理想低通滤波器是个物理不可实现的非因果系统 原因:从()看,K0时已有值
X 第 5 页 1.比较输入输出,可见严重失真; 2.理想低通滤波器是个物理不可实现的非因果系统 几点认识 当 经过理想低通时, 以上的频率成分都衰 减为0,所以失真。 (t) c (t) 1 信号频带无限宽, 而理想低通的通频带(系统频带)有限的 ( ) 0 ~ c 系统为全通网络,可以 无失真传输。 当c → 时,h(t) (t) 原因:从h(t)看,t<0时已有值

三. 理想低通的阶跃响应 激励 e(t)=u(t)→π(o)+ 系统 I.e-iot )H(o)= 0 o>0。 响应 r(t)=u(t)*h(t) 新以o=or司 (-0.<0<0e) =Faol-z上8oj片deao 元)-ei-ao+ ej@(t-) 21 d 1)sinx d x 令x=ot-t
X 第 6 页 ( ) = − c c j 0 1 e ( ) j 0 t h t H ( ) ( ) 0 j e j 1 π t R − 所 以 = + ( ) −c c − − − = = + c 0 e e d j 1 π ( ) 2π 1 ( ) ( ) 1 j j c t t r t F R 三.理想低通的阶跃响应 ( ) ( ) ( ) d j e 2π 1 π e d 2 1 c c 0 c c 0 j j − − − − = + t t t t ( ) d sin 2π 2 2 1 c 0 0 − = + t t ( ) 0 令x = t − t ( ) x x t t x d sin π 1 2 1 c 0 0 − = + 激励 ( ) j 1 e(t)=u(t) π + 系统 响应 r(t) = u(t) h(t)

正弦积分 sin x Sk)ax 34机 1.下限为0: 2.奇偶性:奇函数。 si()】 2 3.最大值出现在x=元 最小值出现在x=元 0 2 合UD风
X 第 7 页 x sin x x 1 O π 2π 3π 4π Si( y) O y 2 π 2 π − 1. 下限为0; 2. 奇偶性:奇函数。 正弦积分 y x x x y 0 d sin Si( ) = 3 . 最大值出现在 最小值出现在 x =π x = −π
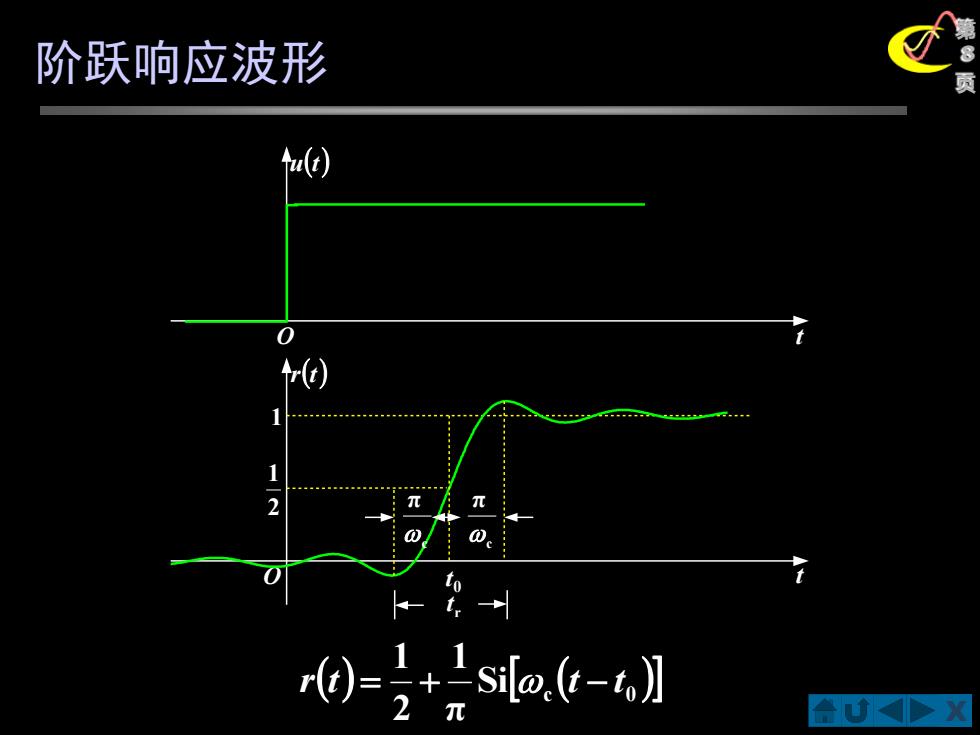
阶跃响应波形 a 0 r() 2 0-+量sot-】 合心4>
X 第 8 页 ( ) ( ) Si c 0 π 1 2 1 r t = + t − t 阶跃响应波形 O t u(t) 1 r(t) O t 2 1 0 t r t c π c π

几点认识 r() 最大值位置:t+ 最小值位置:t 元 立t为系统延迟时间 1·上升时间:输出由最小值到最大值所经历的时间 记作1 π1 t,=2. ⊙。B B= 0=f B是将角频率折合为频率的滤波器带宽(截止频率 。 2.阶跃响应的上升时间t,与网络的截止频率B(带宽) 成反比Bt=1。演示
X 第 9 页 2.阶跃响应的上升时间t r 与网络的截止频率B(带宽) 成反比 B t r = 1 。 B t π 1 2 c r = = c c 2π B = = f B是将角频率折合为频率的滤波器带宽(截止频率)。 几点认识 1.上升时间:输出由最小值到最大值所经历的时间, : r 记作 t X c t π 最大值位置:0 + c t π 最小值位置:0 − t 0 为系统延迟时间 1 r(t) O t 2 1 0 t r t c π c π
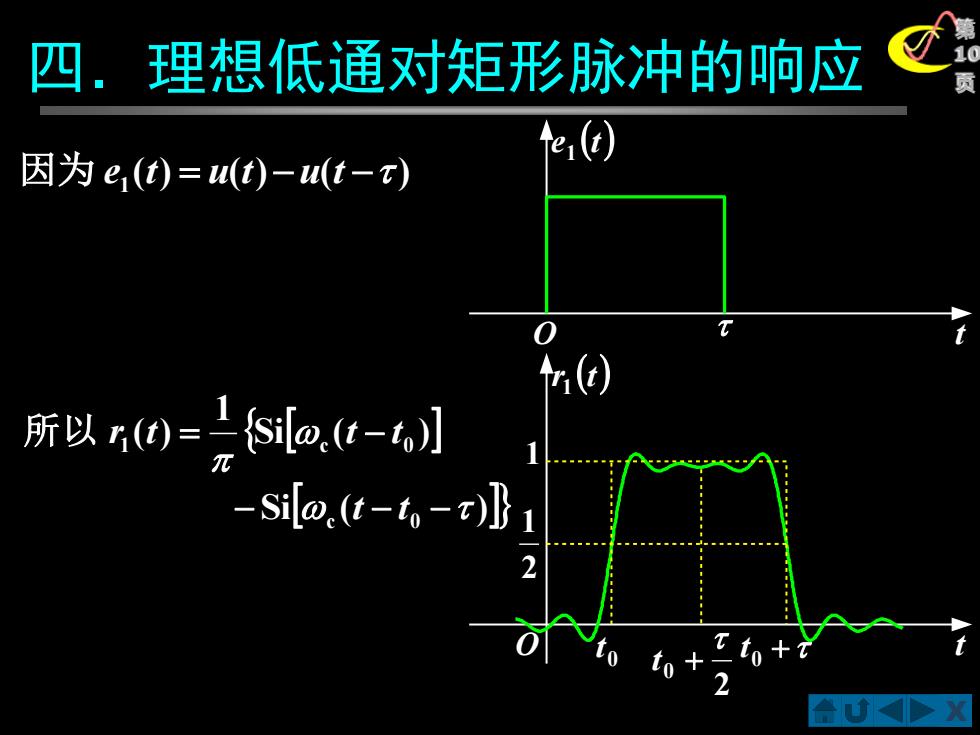
四 .理想低通对矩形脉冲的响应 er (t 因为e(t)=(t)-(t-) i ( 所以r0={Si@.(t-] sio.t-。-x)l1 合心
X 第 10 页 ( ) ( ) ( ) 1 因为 e t = u t − u t − 四.理想低通对矩形脉冲的响应 Si ( ) Si ( ) 1 ( ) c 0 1 c 0 − − − = − t t 所 以 r t t t t e (t) 1 O r (t) 1 t 0 t + 0 t 2 0 t + O 1 2 1