
心号与事我 m4.13 §4.12拉普拉斯变换与傅里叶变 换的关系 米 新疆大学信息科学与工程学院电子系 2011.1 退出 开始
新疆大学信息科学与工程学院电子系 2011.1 §4.12 拉普拉斯变换与傅里叶变 换的关系 4.13

引言 我们在引出拉氏变换时,是针对f()不满足绝对 可积条件,对其乘以一个衰减因玉,作傅氏变换 演变为拉氏变换 [fl=Fy0e'小=Fs)n 由此可以得到傅氏变换与拉氏变换的关系 当o。>0时,收敛边界落右半平面 当σ。<0时,收敛边界落于玉左半平面 当σ。=0时,收敛边界位于虚轴
X 第 2 页 ( ) 演变为拉氏变换 可积条件 对其乘以一个衰减因子 作傅氏变换 我们在引出拉氏变换时 是针对 不满足绝对 , e , , , t f t − ( ) ( ) e ( ) ( ) s σ jω σ t L f t F f t u t F s = + − = = 由此可以得到傅氏变换与拉氏变换的关系 当σ0 0时,收敛边界落于s 右半平面 当σ0 0时,收敛边界落于s左半平面 当σ0 = 0时,收敛边界位于虚轴 引言
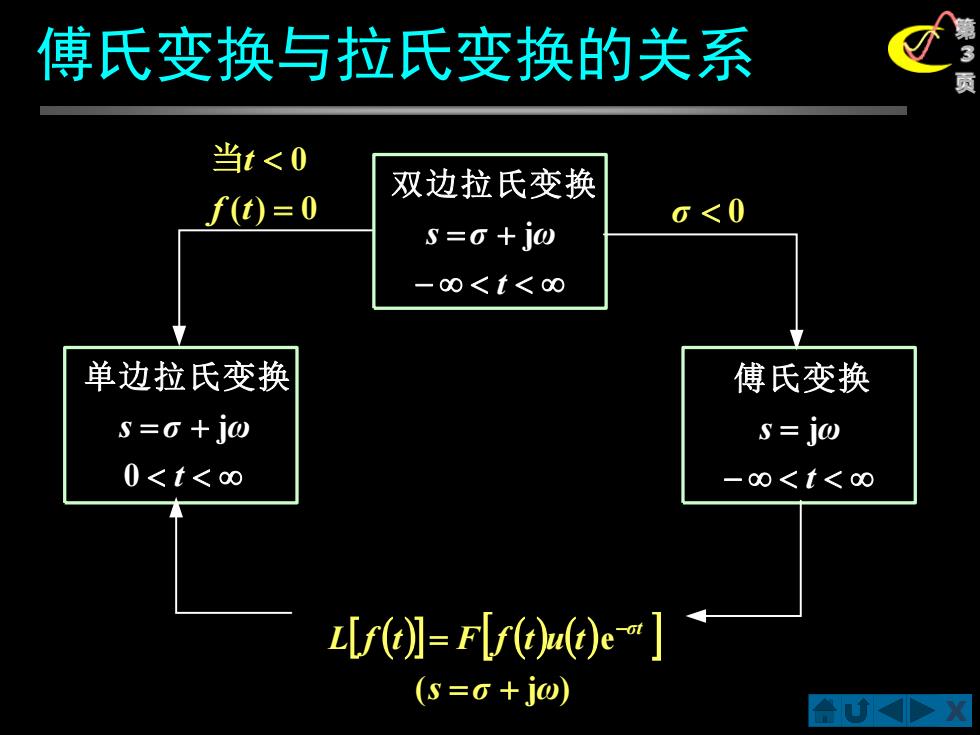
傅氏变换与拉氏变换的关系 当t<0 双边拉氏变换 f(t)=0 0<0 S=o+jω -0<t<0 单边拉氏变换 傅氏变换 S=0+jω S=jω 0<t<o -0<t<0 L[r】=Frt)d)e"] (s=0+j@)
X 第 3 傅氏变换与拉氏变换的关系 页 − = + t s σ jω 双边拉氏变换 − = t s jω 傅氏变换 = + t s σ ω 0 j 单边拉氏变换( ) 0 0 = f t 当t σ 0 ( ) ( ) ( ) ( j ) e s σ ω L f t F f t u t σt = + = −
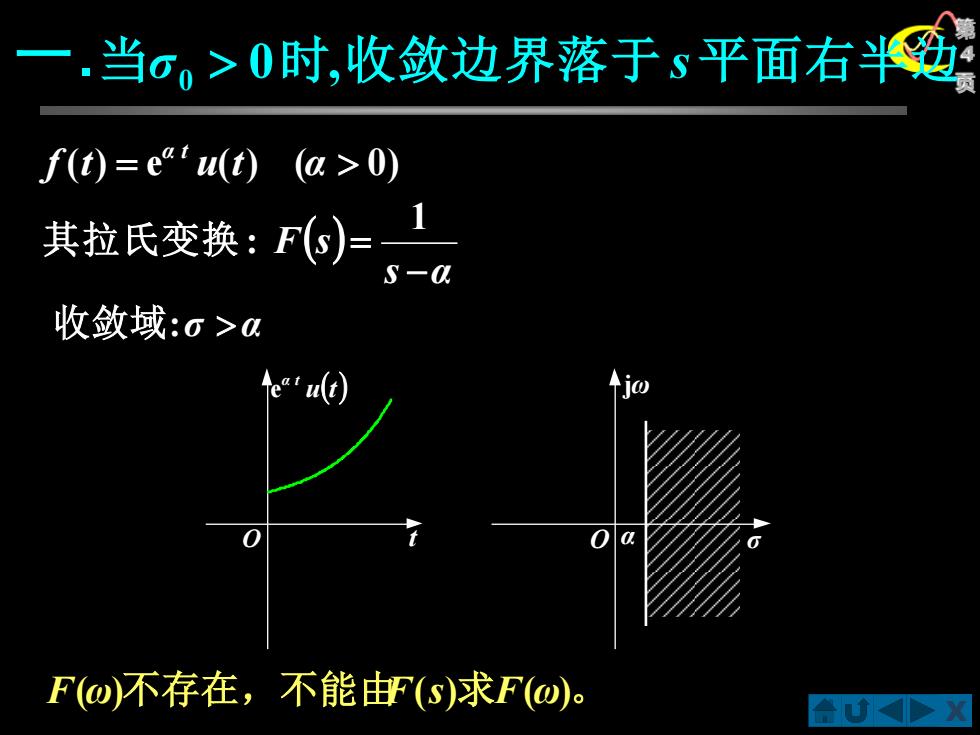
一.当σ。>0时,收敛边界落于s平面右半劲 f(t)=e&'(t)(a>0) 其拉氏变换:F(S)= S- 收敛域:o>a e"'ult 0 F(@不存在,不能由(s)求F@)
X第4 一. 页 O σ jωα 当 σ 0 0 时,收敛边界落于 s平面右半边 f ( t ) = e u ( t ) (α 0 ) α t ( ) s α F s − = 1 其拉氏变换 : F(ω)不存在,不能由F ( s ) 求F (ω ) 。 收敛域 : σ α O t u (t ) α t e
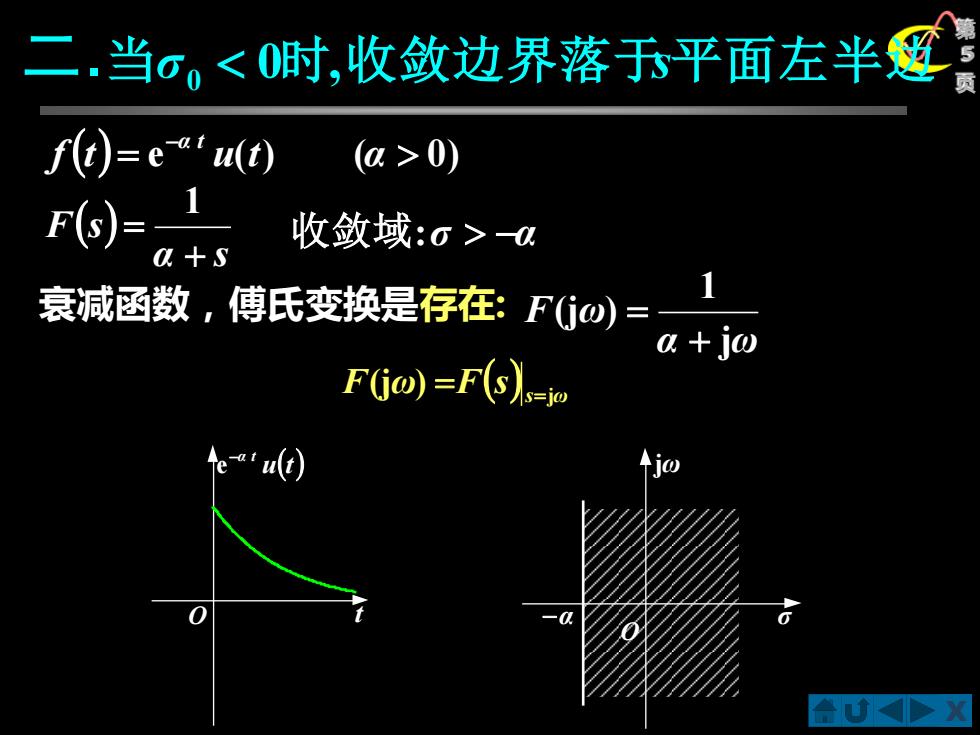
二.当σ。0) 收敛域:σ>a 衰减函数,傅氏变换是存在:Fo)= a +jo F(jo)=F(s)
X 第 5 二. 页 O σ jω O t −α u(t) −α t e 当σ0 0时,收敛边界落于s平面左半边 ( ) = e ( ) ( 0) − f t u t α α t 衰减函数,傅氏变换是存在: ( ) 1 α s F s + = j 1 (j ) α ω F ω + = 收敛域:σ −α ( )s ω F ω F s j (j ) = =

三.当σ。=0时,收敛边界位于虚轴 F(S)是存在的,Fo)与F(s之间不再是简单的置铁系 因为傅氏变换中包括崭函数项。 例如fd)=) r=,FGo=π(@ jo 当初求阶跃函数的傅氏变换,不是用经典法(定义 式),而是用取极限的方法(矩形脉冲的周期为无穷 大)引入了冲激函数而得到的。 那么如何F(s求F(jo?
X 第 6 三. 当 时 收敛边界位于虚轴 页 0 , σ0 = ( ) ( ) ( ) 因为傅氏变换中包括奇异函数项。 F s 是存在的,F ω 与F s 之间不再是简单的置换关 系, f (t) = u(t) ( ) , 1 s F s = j 1 F(j ) = π ( ) + 例如: 当初求阶跃函数的傅氏变换,不是用经典法(定义 式),而是用取极限的方法(矩形脉冲的周期为无穷 大)引入了冲激函数而得到的。 那么如何由F(s)求F(jω)?

那么如何F(s)求Fo): 对于只有一阶极点的情况,极点位于虚轴 由FS出发,将其展开成部分分式 4=F-∑. ,Go,为极点 s-jo 则 FLf(t川=F(sl=jo+元∑kno-0) (4-162 一系列冲激之和: FS中以jo代s 每个一阶极点位于=jo,处 每个冲激函数与每个极点相对应 而冲激函数之强度为πk. 侧题 侧题
X 第 7 页 ,(j ) j [ ( )] ( ) n 为极点 n n n ω s ω k L f t F s − = = [ ( )] ( )| π ( ) = s=jω + n δ ω− ωn F f t F s k 由F(s)出发 ,将其展开成部分分式: 对于只有一阶极点的情况,极点位于虚轴 那么如何由F(s)求F(ω)? F(s)中以 j 代 s π . , j , k s n 而冲激函数之强度为 每个冲激函数与每个极 点相对应 每个一阶极点位于 处 一系列冲 激之和: = (4-162) 则

证明根据变换的惟一性(F(s)→f()→FGo) Pto归F2.eao 线侄,卷积定理∑.f水小Paue】 -25bao-e+ =F(sl=io+∑knπw-on)
X 第 8 证明 根据变换的惟一性 页 − = n n n s ω k F s j ( ) ( ) = n ω t n F ω F k u t n j e ( ) j 线性,卷积定理 = − + n n n ω k δ ω ω δ ω j 1 2π ( ) π ( ) 2π 1 + − − = n n n n n n k δ ω ω ω ω k π ( ) j( ) 1 = = + − n s ω n δ ω ωn F(s)| k π ( ) j (F(s) → f (t) → F(jω)) = n ω t n f t k u t n ( ) e ( ) j n ω t n k F F u t n e ( ) 2π 1 j

四.总结 对于有起因信号,求单边拉氏变换中,一般是>0的 信号,所以收敛域在收敛轴右边。对Fs)分解因式,找 出极点。收敛域中不应有极点,最右边的极点为收敛坐 标。 F(S和FGo)的关系: σ。>0,收敛轴位平面的右半平面则Fo不存在 o<0,收敛轴位玉平面的左半平面则Fo)=F(Sp σ。=0,收敛轴位于虚轴 则F)=Fn+x∑lo-a,)
X 第 9 四.总结 页 对于有起因信号,求单边拉氏变换中,一般是t>0的 信号,所以收敛域在收敛轴右边。对F(s)分解因式,找 出极点。收敛域中不应有极点,最右边的极点为收敛坐 标。 F(s)和F(jω)的关系: ( ) = ( ) + ( − ) = n s ω n δ ω ωn F ω F s k j 则 ( ) ( ) s ω σ s F ω F s 0 j 0, , 收敛轴位于 平面的左半平面则 = = σ0 0,收敛轴位于s平面的右半平面,则F(ω)不存在 σ0 = 0,收敛轴位于虚轴