
心号与事我 §5,3无失真传输 失直 无迭真传输条件 利用失真一波形形成 *米 新疆大学信息科学与工程学院电子系 2003.1 退出 开始
新疆大学信息科学与工程学院电子系 2003.1 §5.3 无失真传输 •失真 •无失真传输条件 •利用失真——波形形成

失真 信号经系统传输,要受到系统函数H(o的加权,输出 波形发生了变化,与输入波形不同,则产生失真。 线性系统引起的信号失真由两方面的因素造成 。幅度失真:各频率分量幅度产生不同程度的衰减; ○相位失真:各频率分量产生的相移不与频率成正比, 使响应的各频率分量在时间轴上的相对位置产生变化。 线性系统的失真—幅度,相位变化,不产生新的频 率成分; 非线性系统产生非线性失真一产生新的频率成分。 对系统的不同用途有不同的要求: 无失真传输;。利用失真—波形变换。 合UDN
X 第 2 一.失真 页 线性系统引起的信号失真由两方面的因素造成 ●幅度失真:各频率分量幅度产生不同程度的衰减; ●相位失真:各频率分量产生的相移不与频率成正比, 使响应的各频率分量在时间轴上的相对位置产生变化。 信号经系统传输,要受到系统函数 的加权,输出 波形发生了变化,与输入波形不同,则产生失真。 H(j) ●线性系统的失真——幅度,相位变化,不产生新的频 率成分; ●非线性系统产生非线性失真——产生新的频率成分。 对系统的不同用途有不同的要求: ●无失真传输;●利用失真⎯⎯波形变换
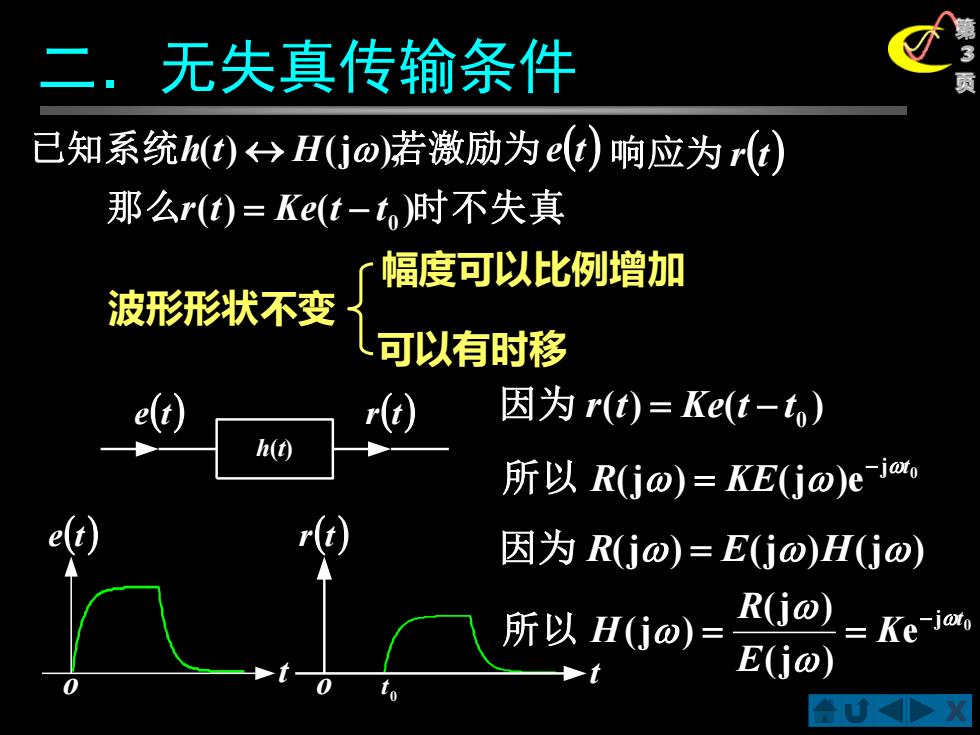
二.无失真传输条件 已知系统d)H(jo)若激励为e(t)响应为rd) 那么r(t)=Ke(t-t,时不失真 幅度可以比例增加 波形形状不变 可以有时移 r() 因为r(t)=Ke(t-t) h() 所以RGo)=KE(jo)eja, 因为R(jo)=E(jo)H(jo) 所以HUo)= R(jo) =Ke-joto E(jo)
X 第 3 二.无失真传输条件 页 幅度可以比例增加 可以有时移 波形形状不变 h(t) e(t) r(t) r(t) o t 0 t e(t) o t 因为 R(j) = E(j)H(j) ( ) ( )0 因为 r t = Ke t − t 0 j (j ) (j )e t R KE − 所 以 = 0 j e (j ) (j ) (j ) t K E R H − 所 以 = = 已知系统h(t) H(j),若激励为 e(t) 响应为 r(t) 那 么r(t) = Ke(t − t 0 )时不失真

频谱图 即:i@y-k (Go】 ↑p(o lpw)=-@t 几点认识: ●要求幅度为与频率无关的常数K,系统的通频带为无 限宽。 ●相位特性与o成正比,是一条过原点的负斜率直线。 ●不失真的线性系统其冲激响应也是冲激函数
X 第 4 页 ( ) = − = 0 (j ) : t H K 即 频谱图 几点认识: ●要求幅度为与频率无关的常数K,系统的通频带为无 限宽。 ●相位特性与 成正比,是一条过原点的负斜率直线。 ●不失真的线性系统其冲激响应也是冲激函数。 O H(j) K O () 0 −t

相位特性为什么与频率成正比关系? Hjo=KeKδt-,)=d) 只有相位与频率成正比,方能保证各谐波有相同的延 迟时间,在延迟后各次谐波叠加方能不失真。 延迟时间,是相位特性的斜率: dpo) 群时延 dw 或称群延时 dpa) T三 do 在满足信号传输不产生相位失真的情 况下,系统的群时延特性应为常数
X 第 5 相位特性为什么与频率成正比关系? 页 H K K (t t ) h(t) t = − = − 0 j 0 (j) e 只有相位与频率成正比,方能保证各谐波有相同的延 迟时间,在延迟后各次谐波叠加方能不失真。 延迟时间t0 是相位特性的斜率: ( ) 0 d d = −t 群时延 或称群延时 ( ) d d = − 在满足信号传输不产生相位失真的情 况下,系统的群时延特性应为常数
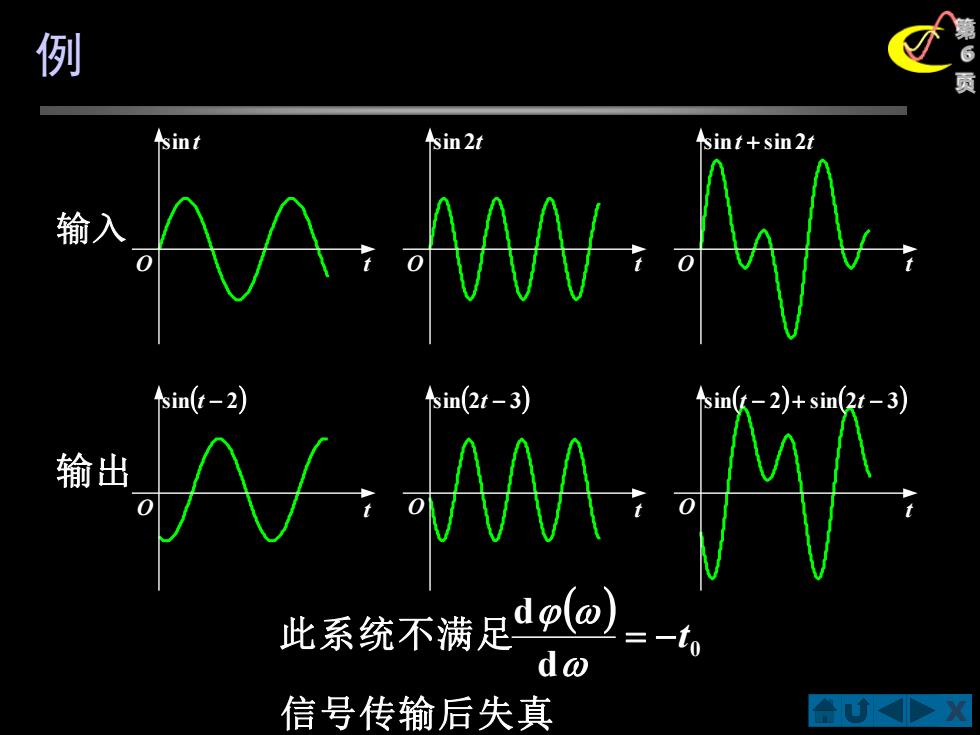
sint sin 2t sint+sin 2t AA:AAA sin(t-2) 个im(2t-3) sin(t-2)+sin(2t 输出 此系统不满足dp(@】 do 信号传输后失真 合UD
X第6 例 页 ( ) 信号传输后失真 此系统不满足 0 d d = − t sint O t O t sin2t O t sint + sin2t sin(t − 2) O t O t sin(2t − 3) O t sin(t − 2) + sin(2t − 3) 输 入 输 出

三.利用失真 波形形成 H(Gjo) Ejo)-1 R(ja)=H(jo) 合U风
X 第 7 三.利用失真——波形形成 页 (t) E(j) = 1 H(j) r(t) R(j) = H(j)

总结 系统的无失真传输条件 时域: h(t)=K8(t-to) 频域: H(j@)=Ke-ioto 即H(Go)=K,p(@)=-0t, K和t均为实常数
X 第 8 总结 页 系统的无失真传输条件 : ( ) ( ) 0 时域 h t = K t − t 0 j : (j ) e t H K − 频域 = 0 即H(j) = K,() = −t K和t 0 均为实常数