
心号与系安 四☐410 §49全通温数与最小相移温数 的零、极点分布 全通网络 •最小相移网络 级联 新疆大学信息科学与工程学院电子系 2011.1 退出 开始
新疆大学信息科学与工程学院电子系 2011.1 §4.9 全通函数与最小相移函数 的零、极点分布 4.10 •全通网络 •最小相移网络 •级联 4.10
全通网络 所谓全通是指它的幅频特性为常数,对于全部频率的 正弦信号都能按同样的幅度传输系数通过。 零、极点分布 极点位于左半平面 零点位于右半平面, ·零点与极点对于虚轴 互为镜像 P2
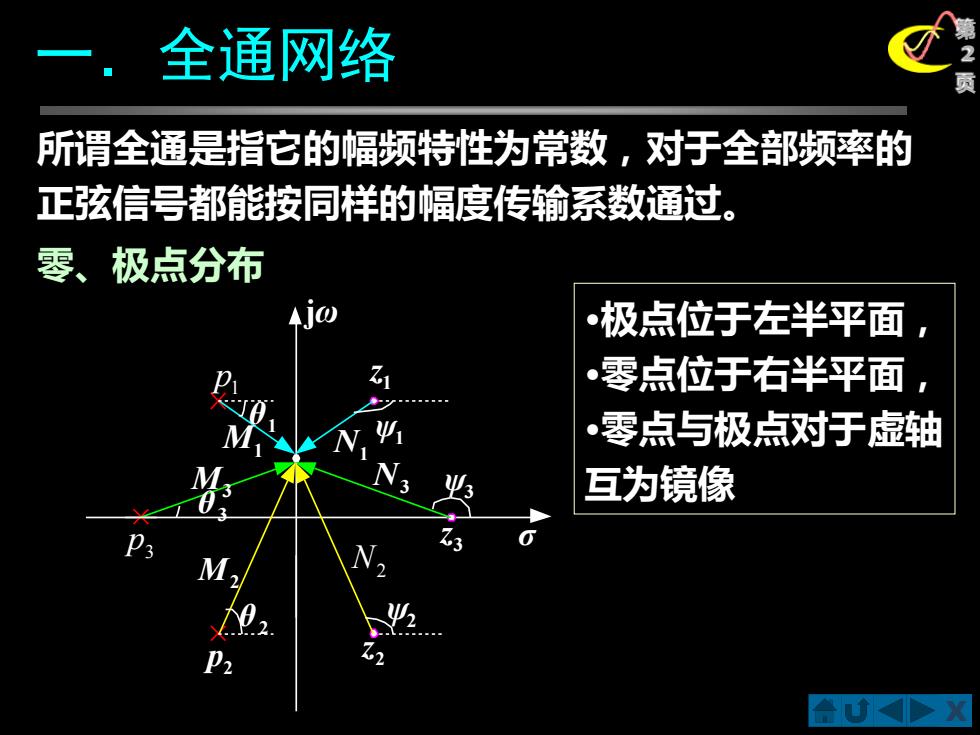
X 第 2 一.全通网络 页 所谓全通是指它的幅频特性为常数,对于全部频率的 正弦信号都能按同样的幅度传输系数通过。 零、极点分布 θ2 ψ2 θ1 ψ1 θ3 ψ3 M1 N1 N2 N3 M2 M3 p3 2 p p1 1 z 3 z 2 z jω σ •极点位于左半平面, •零点位于右半平面, •零点与极点对于虚轴 互为镜像

频率特性 H(o)=&YN,-e),w,】 M MM: =Kew,wB,0,t,】 由于N,N2N,与M,M2M,相消,幅频特性等于常数K,即 H(jo)=K 幅频特性一 常数 相频特性—不受约束 •全通网络可以保证不影响待传送信号的幅度频谱特性, 只改变信号的相位频谱特性,在传输系统中常用来进行 相位校正,例如,作相位均衡器或移相器
X 第 3 频率特性 页 •幅频特性——常数 •相频特性——不受约束 •全通网络可以保证不影响待传送信号的幅度频谱特性, 只改变信号的相位频谱特性,在传输系统中常用来进行 相位校正,例如,作相位均衡器或移相器。 ( ) ( ) ( ) ( ) ( ) 1 2 3 1 2 3 1 2 3 1 2 3 j j 1 2 3 1 2 3 e j e ψ ψ ψ θ θ θ ψ ψ ψ θ θ θ K M M M N N N H ω K + + − + + + + − + + = = 由于N1N2N3与M1M2M3相消,幅频特性等于常数K,即 H(jω) = K
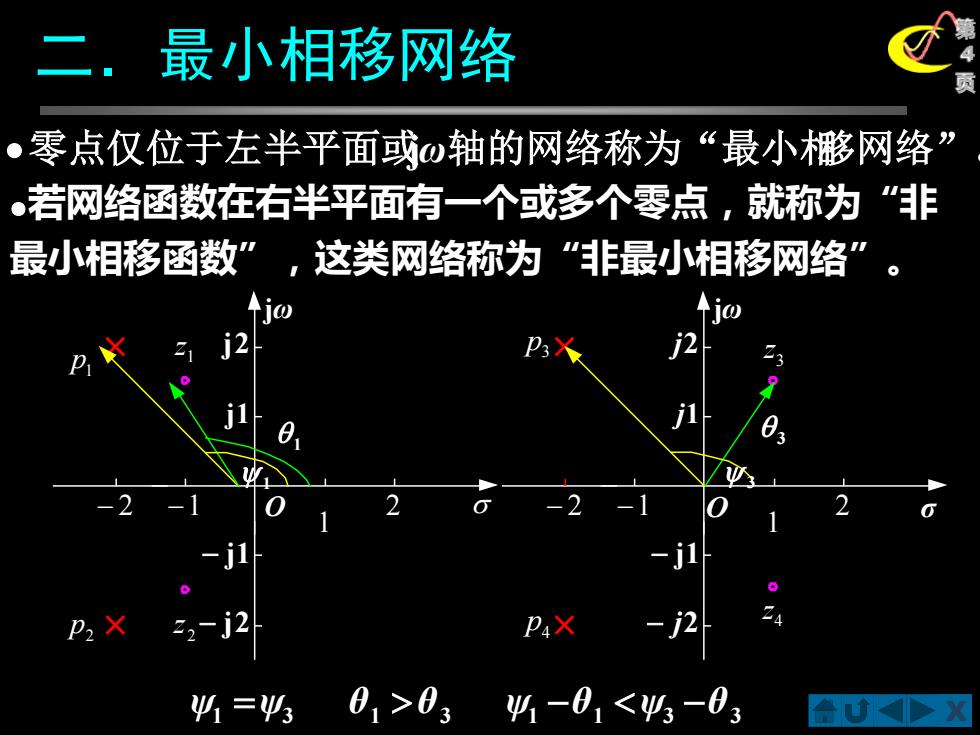
二.最小相移网络 ●零点仅位于左半平面或w轴的网络称为“最小膨网络” 。若网络函数在右半平面有一个或多个零点,就称为“非 最小相移函数”,这类网络称为“非最小相移网络”。 0 P4) 41=43 01>0341-01<4-03
X 第 4 二.最小相移网络 页 jω 1 − 2 −1 2 j2 − j2 j1 − j1 p1 2 p 1 z 2 z O 1 1 σ jω 1 − 2 −1 2 j2 − j2 j1 − j1 p3 p4 3 z 4 z •零点仅位于左半平面或jω轴的网络称为“最小相移网络”。 ●若网络函数在右半平面有一个或多个零点,就称为“非 最小相移函数”,这类网络称为“非最小相移网络” 。 3 3 ψ1 =ψ3 θ1 θ3 ψ1 −θ1 ψ3 −θ3 O

三.级联 非最小相移网络可代之以最小相移网络与全通网络的 级联。 jω jo, 0 0 非最小相移网络 最小相移网络 全通网络 非最小相 +oj 移函数 最小相移函数 全通函数
X 第 5 三.级联 页 1 z 2 z ωj j ωj − j O σ j jω 1 z 2 z σ ωj j O jω ωj − j −σ j 非最小相移网络可代之以最小相移网络与全通网络的 级联。 ωj j ωj − j O σ j jω −σ j 非最小相移网络 最小相移网络 全通网络 ( ) ( )( ) ( ) ( ) 全通函数 最小相移函数 移函数 非最小相 2 2 2 2 2 2 min j j j j j j s σ ω s σ ω H s H s s σ ω + + − + = + +