
心号与系型 §6.4宪备正交品数集、 帕塞瓦尔定理 完备正交函数集 帕塞瓦尔定理 新疆大学信息科学与工程学院电子系 2003.1 退出 开始
新疆大学信息科学与工程学院电子系 2003.1 §6.4 完备正交函数集、 帕塞瓦尔定理 •完备正交函数集 •帕塞瓦尔定理

完备正交函数集 0=c8(④+c8,0+c,8,0++c8,0=∑c,8,@) 定义1: 当n增加时e2下降,若→oo,则e2-→0,此时g1(d, 8,(d)g,(d)gn为完备的正交函数集。 定义2: 如果存在函数()有g,()·x(0dt=0,则x)必属 于此正交函数集,原函数集g(d,g(d)g,(d)gn(t) 不完备
X 第 2 页 定义1: 定义2: 一.完备正交函数集 = = + + + + = n r r r n n r r f t c g t c g t c g t c g t c g t 1 1 1 2 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )为完备的正交函数集。 当 增加时,下降,若 , 则 ,此时 g t g t g t n n g t 2 r n 1 2 2 → → 0 , ( ) ( ) ( ) ( ) ( ) ( ) 不完备。 于此正交函数集,原函数 集 如果存在函数 有 , 则 必 属 g t g t g t g t x t g t x t t x t r n t t r 1 , 2 , ( ) ( )d 0 2 1 =
二.帕塞瓦尔定理 jr(ar->c:jgi(ar-EJC.s.Far 证明 信号的 基底信号的 各信号分量的 能量 能量 能量 物理意义: 一个信号所含有的能量(功率)恒等于此信号在 完备正交函数集中各分量能量(功率)之和。 数学本质:矢量空间信号正交变换的范数不变性
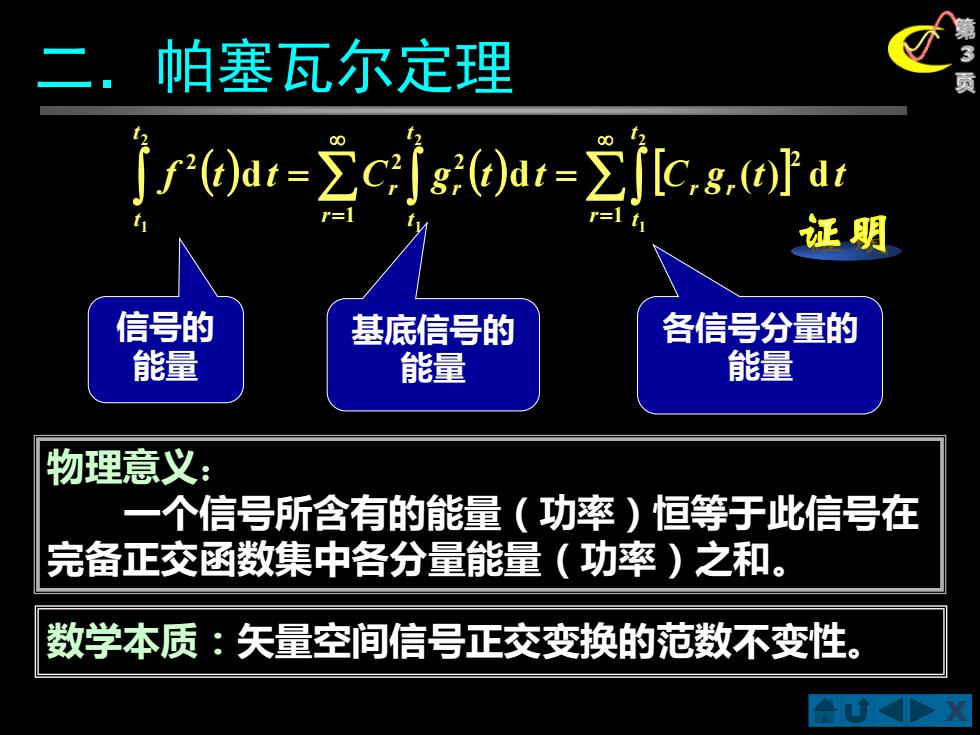
X 第 3 二.帕塞瓦尔定理 页 物理意义: 一个信号所含有的能量(功率)恒等于此信号在 完备正交函数集中各分量能量(功率)之和。 ( ) ( ) = = = = 1 2 1 2 2 2 2 1 2 1 2 1 d d ( ) d r t t r r r t t r r t t f t t C g t t C g t t 信号的 能量 基底信号的 能量 各信号分量的 能量 数学本质:矢量空间信号正交变换的范数不变性