
心号与素安 §3,9周期信号的傅里叶变换 新疆大学信息科学与工程学院电子系 2011.1 退出 开始
新疆大学信息科学与工程学院电子系 2011.1 §3.9 周期信号的傅里叶变换

主要内容 正弦信号的傅里叶变换 ·一般周期信号的傅里吐变换 如▣由E(@)求Fn@) ·单位冲激序列的傅压变换 ·周期矩形脉冲序列的傅氏变换
X 第 2 主要内容 页 •正弦信号的傅里叶变换 •一般周期信号的傅里叶变换 •如何由F0 (ω)求F(nω1 ) •单位冲激序列的傅氏变换 •周期矩形脉冲序列的傅氏变换

引言 周期信号: fd)傅里叶级数-F(no) 离散谱 非周期信号: f(d)分傅里叶变换-F(o) 连续谱 周期信号的傅里叶变换如何求? 与傅里叶级数的关系? f 周期 统一的分析方法:傅里叶变换 非周期 合UD
X 第 3 页 周期信号: 非周期信号: 周期信号的傅里叶变换如何求? 与傅里叶级数的关系? f (t) 傅里叶级数− F(n1 ) 离散谱 f (t) 傅里叶变换− F() 连续谱 ( ) 统一的分析方法:傅里叶变换 非周期 周 期 f t 引言

正弦信号的傅里叶变换 由欧拉公式 sn=2kr-e) 1 已知 12m6(o) 由频移性质 1eo'2ro-@) 1ej←>2r60+0 c0s@,12r@-@,+2x6o+@,】=xo+@,)+π@-@,) 同理 sin@,t<>-jπ6o-o,)+jπ6o+o,)
X 第 4 页 由欧拉公式 由频移性质 一.正弦信号的傅里叶变换 ( ) ( ) t t t t t t 0 0 0 0 j j 0 j j 0 e e 2 j 1 sin e e 2 1 cos − − = − = + 1 2π () ( ) ( ) 0 j 0 j 1 e 2 1 e 2 0 0 + − − t t ( ) ( ) ( ) ( ) 0 2π 0 2π 0 π 0 π 0 2 1 cos t − + + = + + − 同理 ( ) ( ) 0 0 π 0 sin t − jπ − + j + 已知

频谱图 c0s0,t<>元[8(0+0)+δ(@-@)】 cos@,t频谱图: F(o) 9 00 sino,t>-jπ6(o-o+jπδ(o+@,) sino,t频谱图: 0 (r) ) 0 00 0 2
X 第 5 页 cos π ( ) ( ) 0 +0 + −0 t ( ) ( ) 0 0 π 0 sin t − jπ − + j + −0 0 (π ) (π ) F() O 频谱图 cos : 0 t 频谱图 sin : 0 t 频谱图 −0 0 (π ) (π ) F() o 0 −0 () 2 2 − o

般周期信号的傅里叶变换 设信号周期:T= 2π 01 由傅里叶级数的指数形式出发:f,)=∑Fr@,小k 其傅氏变换用定义) F@)=Flf(t =r2t@k-2rta,r】 =2r(no,)2rdo-n@,) =2r∑F(no,)do-n@,)
X 第 6 页 由傅里叶级数的指数形式出发: 其傅氏变换(用定义) 二.一般周期信号的傅里叶变换 1 1 2π : 设信号周期 T = ( ) ( ) =− = n j n t f t F n 1 e T 1 ( ) ( ) ( ) ( ) n t n t F F n F n F F F f t 1 1 j 1 j 1 T T e e − − = = = ( ) ( ) 1 π 1 = F n 2 − n − ( ) ( ) π 1 1 = 2 F n − n −

几点认识 F,(o)=2r∑F(no,o-n@,) (①f(的频谱由冲激序列组成 位置:0=n01 (谐波频率 强度:2rF(no,)与F(no,)成正比,离散谱 谱线的幅度不是有限值,因为F(⊙表示的是频谱密度 周期信号的F(o)只存在于o=no,处, 频率范围无限小幅度为o
X 第 7 页 (1) ( ) ; f T t 的频谱由冲激序列组成 位置: (谐波频率) = n1 强度: 2π F(n1 ) 与F(n1 )成正比, 离散谱 几点认识 (2) 谱线的幅度不是有限值, 因 为F()表示的是频谱密度。 ( ) , 周期信号的F 只存在于 = n1 处 频率范围无限小,幅度为。 ( ) ( ) ( ) T π 1 1 F = 2 F n − n −
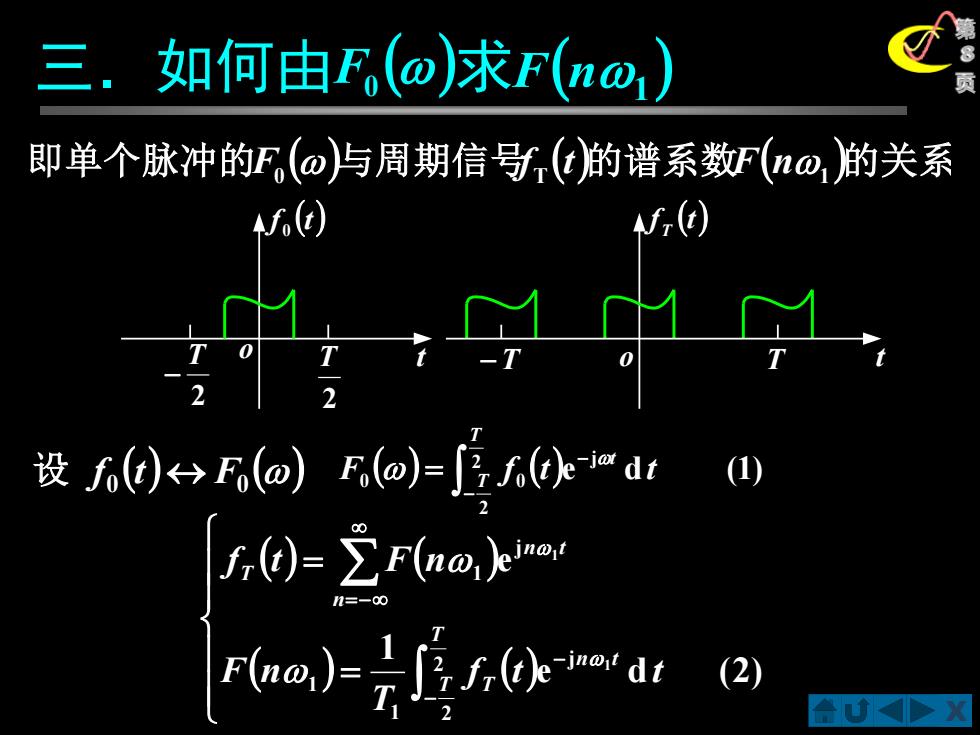
三.如何由F,(o)求F(no) 即单个脉冲的F,(@与周期信号d)的谱系数F(o,的关系 M() f() 0 2 2 设0)ro)ro)-正r伙d:① f-∑Fta@,ee Fa,)度0war (2)
X 第 8 三.如何由 求 页 即单个脉冲的F0 ()与周期信号f T (t)的谱系数F(n1 )的关系 f (t) 0 t 2 T − 2 T f (t) T −T o T t o ( ) () 0 0 设 f t F ( ) ( )e d (1) 2 2 j 0 0 − − = T T t F f t t () F0 ( ) F n1 ( ) ( ) ( ) ( ) = = − − =− 2 2 j 1 1 j 1 e d (2) 1 e 1 1 T T n t T n n t T f t t T F n f t F n

ro)=店严d 了,0)=2r(n@,kr r心@,)r小a: (2) 比较式(1),(2) no 1() ←> ) 内f)与f)湘同所以F(no,)=F(o) @=n@ 可由F,(o求周期函数ft)的谱系数F(no,)
X 第 9 页 比较式(1),(2) ( ) ( ) ( ) ( ) = = − − =− 2 2 j T 1 1 j T 1 e d (2) 1 e 1 1 T T n t n n t f t t T F n f t F n f (t) f (t) n 0 T 1 在 内f (t)与f (t)相同 T T 0 T 2 , 2 − ( ) ( ) 1 0 1 1 1 n F T F n = 所 以 = ( ) ( ) ( ) 0 T F n1 可由F 求周期函数 f t 的谱系数 ( ) ( )e d (1) 2 2 j 0 0 − − = T T t F f t t

四.周期单位冲激序列的傅里叶换 46,() 0000 6,d=∑t-nT) 因为d)→1 所以,的傅氏级数谱系签Fu@,)=7 所以6,)=∑rta@r-∑ n@
X 第 10 页 ( ) ( ) =− = − n T t t nT1 ( ) ( ) =− =− = = n n t n n t T t F n 1 1 j 1 j T 1 e 1 e 所 以 四.周期单位冲激序列的傅里叶变换 t (t) T (1) (1) (1) (1) (1) − 2T1 −T1 T1 2T1 o 因为 (t)1 所以 T (t)的傅氏级数谱系数 ( ) 1 1 1 T F n =