
第4卷第4期 智能系统学报 Vol.4 No.4 2009年8月 CAAI Transactions on Intelligent Systems Ag.2009 doi:10.3969/i.issn.1673-4785.2009.04.013 具有不确定性的非线性系统自适应 神经网络L增益控制 李桂英,魏莹,张扬,孙来军 (黑龙江大学电气工程及其自动化实验室,黑龙江哈尔滨150080) 摘要:针对存在不确定性的非线性系统,提出了自适应神经网络L,增益控制器设计方法,将基于Hamilton-Jacobi- Issacs(HI)不等式和自适应神经网络策略相结合,有效地克服了需要被控对象精确建模的局限性.神经网络对系统 模型的偏差进行拟合;为了补偿拟合误差,引入补偿控制器和神经网络权值自适应调节律,通过在线自适应修正神 经网络权值,来保证闭环系统满足相应的性能准则.仿真结果表明提出的控制器设计方法是有效的,克服了一般 方法需要被控对象精确建模的局限性. 关键词:L2增益;神经网络控制;HΠ不等式 中图分类号:TP273文献标识码:A文章编号:16734785(2009)04-0357-06 An adaptive neural network L-gain controller for nonlinear systems with uncertainty LI Gui-ying,WEI Ying,ZHANG Yang,SUN Lai-jun (Laboratory of Electrical Engineering&Automation,Heilongjiang University,Harbin 150080,China) Abstract:A scheme for an adaptive neural network L2-gain controller was proposed for nonlinear systems with un- certainty.By combining the Hamilton-Jacobi-Issacs(HJI)inequality with an adaptive neural network,limitations on the precision of previous models can be effectively overcome.With this controller,errors from the model were fitted by the neural network.In order to compensate for the fitting errors,a compensation controller and an adaptive law for the weights of the neural network were introduced.By on-line adaptive adjustment of these weights,L2-gain performance of the closed-loop system could be guaranteed.Simulation results are shown to demonstrate the effec- tiveness and the advantages of the proposed approach.To avoid the limitation of the precision model of the plant in the common approach. Keywords:L2-gain;neural network control;HJI inequality 许多与L2增益约束有关的控制问题,如L2综 函数拟合特性可以得到满足HI不等式的解).一 合问题、控制以及L,干扰控制等,都可以归结为使般来说,若不能够获得非线性系统的一个不精确模 系统成为耗散系统的问题.非线性H。控制的经典 型,且对于不确定性不具有太多的先验信息,为了减 方法是基于HI偏微分不等式的方法.对于非线性 轻神经网络对模型的学习负担,要充分利用这些已 系统,假设其L2增益控制器存在,那么控制器设计 有的系统模型信息,让神经网络对系统模型的偏差 问题的关键是如何找到满足HI不等式的存储函 进行拟合.控制器设计的基本思想是在控制器中引 数.虽然解HI偏微分不等式可以获得L2增益控制 入神经网络的可调的权值参数,通过在线自适应修 器,但是一般求HI不等式的解析解比较困难.特别 正该参数来保证整个闭环系统的动态特性, 是对于高阶系统,尚且没有求解HI的一般理论.近 年来,通过神经网络控制得到广泛关注16,利用其 1 问题的描述 收稿日期:200803-21. 考虑下面具有不确定性的非线性系统: 基金项目:黑龙江省自然科学基金资助项目(200707):黑龙江大学 青年科学基金资助项目(QL200736). [E=f(x+△(x)+8(x)u+k(x)w,(1) 通信作者:李桂英.E-mail:lg996032@163.com Ly =h(x)

·358. 智能系统学报 第4卷 式中:x∈R”,u∈R",w∈R,y∈R分别为状态向 [k(x)k(x)- 量、输入向量、干扰输入向量和输出向量;f(x)、 22 g(x),h(x)和k(x)均为适当维数的光滑函数向量 或矩阵;△(x)为未知且有界光滑的函数向量. gegr(enY+(ea≤0 (6) 定义1[剧如果存在常数y≥0和B≥0,对于所 则该系统的L,增益小于或等于y.其中状态反馈控 有的w∈L2[0,T]和T∈[0,o)满足 制律为 yI≤YIw出+B. u=-g(x)o"V/ax. (7) (2) 证明设V(x)≥0为光滑的存储函数,V(x) 则称系统(1)的L2增益小于或等于y,并且称该系 统是有限增益L2稳定.其中L2[0,T]表示扩展的L2 沿该闭环系统轨迹的时间的微分为)-8()+ 空间.‖·‖是Euclidean范数. ()+(+,者)满足m不等式O, av 在定义1中,给出了由外界于扰"到系统输出 则 y=h(x)的L2增益;即w→y的L2增益.Y表示系统 的干扰抑制能力.显然,对于同一干扰,Y越小,系统 立≤-29)s)'(e)-8g 状态偏离平衡点的程度越小;控制系统的干扰抑制问 题可以归结为设计控制器使得L2增益尽可能小于或 -2()()+8¥ r08(x)u+ 等于给定值。 给定的非线性系统(1),鲁棒L2性能准则设计 3兰(m=u+g))1- 问题描述为:对于给定的正数Y,设计神经网络状态 反馈控制器以及未知参数®调节律 2w-e81· u=a(x), (3) 2(y1w2-y2-1u2). ⊙=C(x,⊙) (4) 将式(7)代入上式,得 使得该闭环系统满足如下性能指标: 1)神经网络权值⊙有界,即存在K>0使得 ≤-1w)+ I⊙(t)‖≤K,Ht≥0;同时若系统(f(x)、h(x))是 零状态可检测的,当w=0时,使得imx(t)=0. 2(Iw2-Iy2-Iu2)≤ 2)当w≠0时,对于预先给定的y>0以及任意 (y1w2-1. 的T>0,该系统的L2增益小于Y 从t=0到t=T对上式两边积分,得 2非线性系统L2增益控制器 V(x(T)-V(x(0))≤ L,干扰控制问题都可以归结为闭环系统的耗散 2fYlwIdt-2fIyId 性问题。一般来讲,这类设计问题都需要解适当的 由于V(x)≥0,则 Hamilton-Jacobi-Issacs(HJⅡ)偏微分不等式,这是非线 性Hn控制的经典方法.该结果源于Van der Schaft的 ddt+2v(x(0)).(8) 出色工作9,通过导出一定形式的HI不等式的解, 因此该闭环系统L2增益小于或等于y,其中B= 给出了大量的非线性鲁棒H控制的结果.关于非线 2V(x(0)). 性系统L2增益控制器的设计有如下定理. 3 鲁棒L2增益控制器设计 定理1给定非线性系统: [=f(x)+g(x)u+k(x)w, 根据神经网络的拟和能力,利用神经网络来拟 (5) Ly =h(x). 合非线性系统中存在的不确定性△(x).设控制输 对于任意的y>0,若存在连续可微的半正定函数 入通道与不确定性△(x)之间满足匹配条件,即存 V(x)(称为存储函数),满足HI(Hamilton-Jacobi-- 在适当的函数矩阵S(x|⊙),使得 Issacs)不等式: A(r)=g(x)S(x|⊙)=g(x)⊙p(x)(9) 8)+号8¥ a 成立.其中,神经网络的输出为S(xI⊙)=⊙p(x), 其输人x=(x1x2…xn);⊙=(⊙1⊙2…⊙)T为未知

第4期 李桂英,等:具有不确定性的非线性系统自适应神经网络L2增益控制 ·359· 的神经网络权值矩阵;(x)=(中(x)…中(x)T Mg(x)Ssgn(Mg(x))+tr(-)= 为神经网络的基函数向量;L为神经网络基函数的 M[f(x)+g(x),+k(x)w]+ 个数 Mg(x)(⊙'-⊙)(x)+Mg(x)· 设理想的神经网络权值®·定义如下:⊙*= arg[毁8(x)S(x8)-4(x)I].理想的网络 (-6sgn(Mg(x)+e)+tr{(®-®*)'Θ. 权重⊙*是使得拟合误差|ε|为最小时的神经网络 (16) 权值.其中,神经网络的理想输出为S(x|⊙),神经 如果令权值自适应学习律⑨为 网络的函数拟合误差ε满足: ⑧=(x)Mg(x). (17) △(x)=g(x)(S(xI⊙)+e)= 根据式(17),得 g(x)(⊙Te(x)+ε. (10) 0=M[f(x)+g(x)4,+k(x)w]+ 由于假设不确定性△(x)有界,那么存在一个正 Mg(x)(⊙·-⊙)T(x))- 的常数6作为一个界,即使得‖e‖0 A(x)]+{(8-®)T0}= (x≠x),则根据上式可知系统(1)的平衡点x=0 M[f(x)+g(x)u,+k(x)w]+MA(x)+ 是渐近稳定的.亦有im⊙(t)=⑨*.此时,性能指 Mg(x)u。+r{(®-⊙°)⑧. (14) 标(1)得到满足. 如果令补偿控制器4。为 为了保证自适应调节的神经网络权值⊙(t)有 u。=-S(x|⊙)-6sgm(Mg(x)). (15) 界,定义紧集2,使得神经网络权值⊙(t)满足2,= 并且将式(11)和(15)代入式(14),得 {‖⊙‖≤M。}.其中‖·‖表示向量的2-泛数.根 0=M[f(x)+g(x)u,+k(x)w]+ 据投影算法,将式(17)中的权值自适应学习律®修 Mg(x)(S(xI⊙)-S(xI⊙)+e)- 改如下:

.360. 智能系统学报 第4卷 (x)Mg(x),如果I⊙‖0. (18) -2 修改后的权值调节律可以保证神经网络的权值 有界.下面证明使用投影算法后,对原闭环系统提出 400.51.01.52.02.53.03.54.0 的性能指标仍然能够满足。 tis 当‖⊙‖0时,式 (13)的导数重写为 0=M[f(x)+g(x)u,+k(x)w]+ Mg(x)((⊙-®)'p(x))- Mg(x)(δsgn(Mg(x))-e))+ tr{(⊙-⊙*)Tp(x)Mg(x)}0,并且(f(x),h(x))是零状态可检 因为‖®‖=M>‖®*‖,所以(0-⊙)8= 测的,则存在状态反馈控制器(12)以及权值自适应 3(182-102-10-01)>0,又因 学习律(18)和补偿控制器(15),使得该闭环系统满 为0-9y留e()题()>0. 足提出的性能指标 4仿真分析 所以0<M[f(x)+g(x)4,+k(x)w]由M[f(x)+ 8(x)4,+k()w]≤2Iw2-D),得t< 被控制对象是搅拌式化学反应器.化学反应物 质连续流人反应器中,在冷却剂的控制下,发生化学 2.IwP-号y2,于是有1y12at<. 反应,最终产物不断流出反应器.控制的目的是控制 冷却剂的流量来控制化学反应过程的温度,该被控 ‖w‖2dt+2U(x(0).因此该闭环系统的L2增益 制对象的动态方程描述如下: f(x)=( -2(x(t)+0.25)+(x2(t)+0.5)exp(25x1(t)/(x1(x)+2) 0.5-x2(t)-(x1(t)+0.5)exp(x1(t)+2)) 8(x)=()-0.25 0 状态变量x(t)和x2(t)分别是反应器中的温 度误差和反应物的浓度误差,控制量(t)是冷却剂 的流量.输出方程和干扰增益向量分别为h(x)= 由式(9)得S(xl8°)=8Tp(x)=0.2cos(5x1+ 10x(t),k(x)=(0.10)I.在该系统中引入如下 5rx2),0*=1. 的不确定性 名义控制器为u=-g(x)aV(xIw)/ax,这里
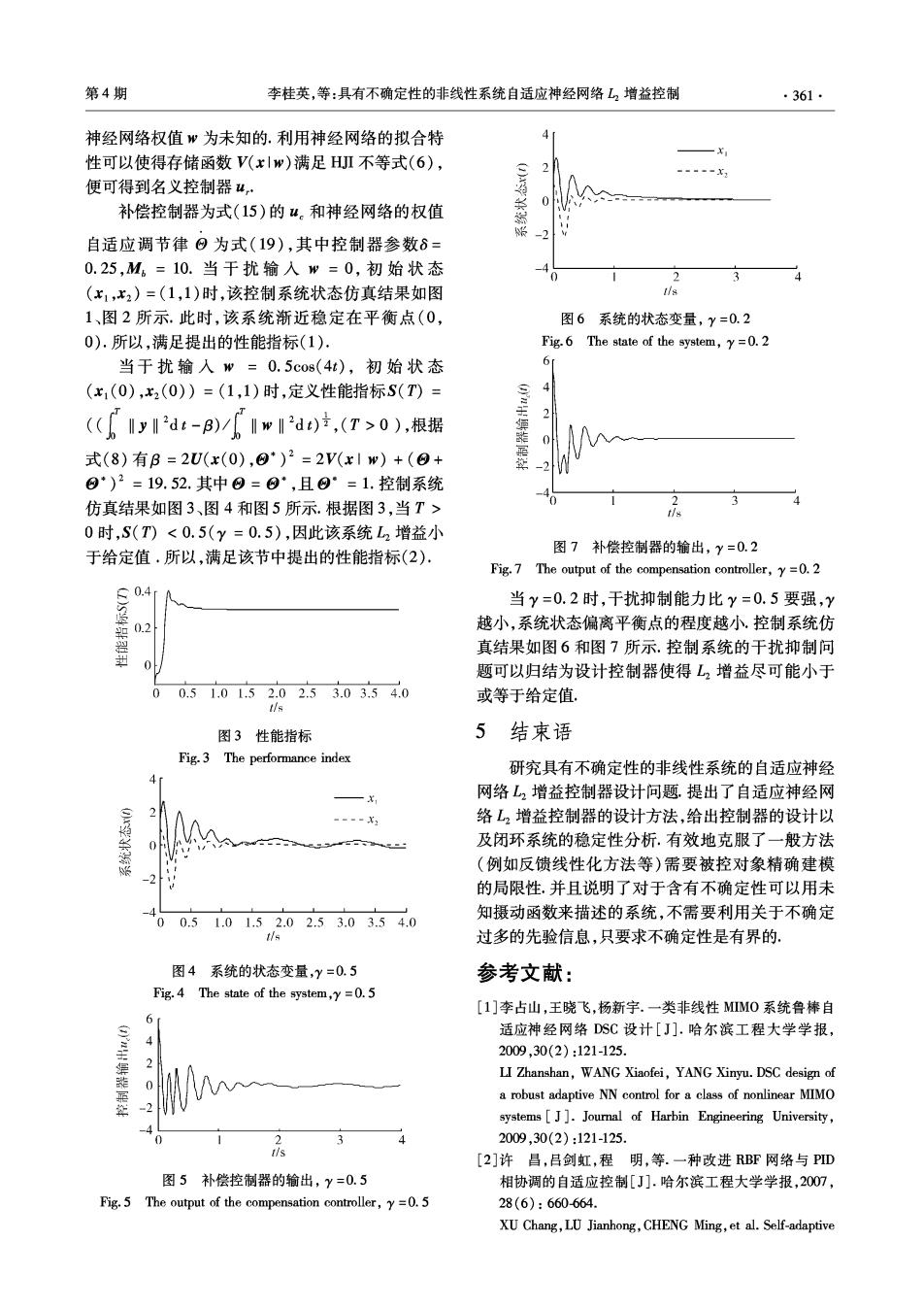
第4期 李桂英,等:具有不确定性的非线性系统自适应神经网络L2增益控制 ·361· 神经网络权值”为未知的.利用神经网络的拟合特 性可以使得存储函数V(x|w)满足HI不等式(6), 2 便可得到名义控制器4· 补偿控制器为式(15)的4。和神经网络的权值 自适应调节律⊙为式(19),其中控制器参数6= 0.25,M。=10.当干扰输入w=0,初始状态 2 (x1,x2)=(1,1)时,该控制系统状态仿真结果如图 1、图2所示.此时,该系统渐近稳定在平衡点(0, 图6系统的状态变量,Y=0.2 0).所以,满足提出的性能指标(1). Fig.6 The state of the system,y=0.2 当干扰输人w=0.5cos(4t),初始状态 (x1(0),2(0))=(1,1)时,定义性能指标S(T)= (IyI2at-B)/Iw2d)立,(T>0),根据 2 式(8)有B=2U(x(0),®*)2=2V(x1w)+(8+ ®·)2=19.52.其中®=8°,且0°=1.控制系统 仿真结果如图3、图4和图5所示.根据图3,当T> t/s 0时,S(T)<0.5(y=0.5),因此该系统L2增益小 于给定值.所以,满足该节中提出的性能指标(2). 图7补偿控制器的输出,y=0.2 Fig.7 The output of the compensation controller,y=0.2 0.4 当y=0.2时,干扰抑制能力比y=0.5要强,y 0.2 越小,系统状态偏离平衡点的程度越小.控制系统仿 真结果如图6和图7所示.控制系统的干扰抑制问 题可以归结为设计控制器使得L2增益尽可能小于 0.51.01.52.02.53.03.54.0 或等于给定值 t/s 图3性能指标 5结束语 Fig.3 The performance index 研究具有不确定性的非线性系统的自适应神经 4 网络L2增益控制器设计问题。提出了自适应神经网 络L2增益控制器的设计方法,给出控制器的设计以 及闭环系统的稳定性分析,有效地克服了一般方法 1 (例如反馈线性化方法等)需要被控对象精确建模 -2 的局限性.并且说明了对于含有不确定性可以用未 0.51.01.52.02.53.03.54.0 知摄动函数来描述的系统,不需要利用关于不确定 tls 过多的先验信息,只要求不确定性是有界的。 图4系统的状态变量,y=0.5 参考文献: Fig.4 The state of the system,y=0.5 [1]李占山,王晓飞,杨新宇.一类非线性MM0系统鲁棒自 6 适应神经网络DSC设计[J].哈尔滨工程大学学报, 2009,30(2):121-125 LI Zhanshan,WANG Xiaofei,YANG Xinyu.DSC design of a robust adaptive NN control for a class of nonlinear MIMO systems[J].Journal of Harbin Engineering University, 2 2009,30(2):121-125. tis [2]许昌,吕剑虹,程明,等.一种改进RBF网络与PID 图5补偿控制器的输出,Y=0.5 相协调的自适应控制[J].哈尔滨工程大学学报,2007, Fig.5 The output of the compensation controller,y=0.5 28(6):660664. XU Chang,LU Jianhong,CHENG Ming,et al.Self-adaptive

.362. 智能系统学报 第4卷 control with coordinated PID and improved RBF network nonlinear state feedback control[J].IEEE Transactions on [J].Joumnal of Harbin Engineering University,2007,28 Automatic Control,1992,37(6):770-784. (6):660664. 作者简介: [3]何文广.基于模糊神经控制的机器人避障算法[J].黑龙 李桂英,女,1974年生,讲师,主要 江工程学院学报,2008,22(3):6366. 研究方向为智能系统、优化算法.发表 HE Wenguang.The caculation of avoiding barriers for robot 学术论文3篇。 based on fuzzy neural control[J].Joumal of Heilongjiang Institute of Technology,2008,22(3):63-66. [4]吴珠,刘国栋.线性不确定离散时滞系统的鲁棒非脆 弱H.控制[J].智能系统学报,2008,3(1):66-70. WU Zhu,LIU Guodong.Robust and non-fragile H control 魏莹,女,1978年生,硕士研究 for linear discrete-time systems with time-delay and uncer- 生,主要研究方向为自动化测试与控 tainties J].CAAI Transactions on Intelligent Systems, 制.发表学术论文2篇. 2008,3(1):66-70. [5]冯筱林,李斌,靳炜,侯东良.一种非线性系统的神 经网络自适应控制[J].应用科技,2007,34(5):39-41. FENG Xiaolin,LI Bin,JIN Wei,HOU Dongliang.Adaptive control of a kind of nonlinear system using neural networks 张扬,男,1982年生,硕士研究 [J].Applied Science and Technology,2007,34(5):39-41. 生,主要研究方向为微控制器及嵌入式 [6]张子迎,刘心,杨霁.基于神经网络PID的AUV控制 系统应用.发表学术论文3篇. 方法研究[J].应用科技,2007,34(8):25-28. ZHANG Ziying,LIU Xin,YANG Ji.AUV's motion control based on NN PID [J].Applied Science and Technology, 2007,34(8):25-28. [7]AHMED M S.Neural controllers for nonlinear state feed- 孙来军,1977年生,男,博士,讲师, back L-gain control C]//Control Theory and Applica- 硕士生导师,主要研究方向为设备监测 tions.United Kingdom,2000,147(3):239-246. 与故障诊断技术、无损检测技术, [8]HASSAN H K.非线性系统[M].3版.北京:电子出版 社,2005:141-154. 9]SCHAFT A J.L-gain analysis of nonlinear systems and 第7届神经网络国际研讨会 Seventh International Symposium on Neural Networks ISNN 2010) The Seventh International Symposium on Neural Networks (ISNN 2010)will be held in Shanghai,following the suc- cesses of previous events.Shanghai is the largest city in China,located in her eastem coast at the outlet of the Yangtze River.Originally a fishing and textiles town,Shanghai grew to importance in the 19th century.In 2005 Shanghai became the world's busiest cargo port.The city is an emerging tourist destination renowned for its historical landmarks such as the Bund and Xintiandi,its modem and ever-expanding Pudong skyline including the Oriental Pearl Tower,and its new repu- tation as a cosmopolitan center of culture and design.Today,Shanghai is the largest center of commerce and finance in mainland China,and has been described as the"showpiece"of the world's fastest-growing economy.In addition,Shang- hai is the venue of forthcoming World Expo 2010 to take place from May 1 to October 31.ISNN 2010 aims to provide a high-level intemational forum for scientists,engineers,and educators to present the state of the art of neural network re- search and applications in related fields.The symposium will feature plenary speeches given by world renowned scholars, regular sessions with broad coverage,and special sessions focusing on popular topics. Prospective authors are invited to contribute high-quality papers to ISNN 2010.In addition,proposals for special ses- sions within the technical scopes of the symposium are solicited.Special sessions,to be organized by internationally recog- nized experts,aim to bring together researchers in special focused topics.Papers submitted for special sessions are to be peer-reviewed with the same criteria used for the contributed papers.Researchers interested in organizing special sessions are invited to submit formal proposals to ISNN 2010.A special session proposal should include the session title,a brief description of the scope and motivation,names,contact information and brief biographical information on the organizers. Website:http://isnn2010.mae.cuhk.edu.hk