机器学习：切换回归模型的抗噪音聚类算法

第4卷第6期 智能系统学报 Vol.4 No.6 2009年12月 CAAI Transactions on Intelligent Systems Dec.2009 doi:10.3969/i.issn.1673-4785.2009.06.005 切换回归模型的抗噪音聚类算法 杨小兵，何灵敏，孔繁胜 (1.中国计量学院计算机系，浙江杭州310018；2.浙江大学计算机学院，浙江杭州310012》 摘要：对切换回归模型的聚类方法一般都没有考虑到噪音的影响，因此在含有噪音数据的情况下，用这些方法聚 类的结果就会出现一定的偏差.为了减弱聚类过程中噪音数据的影响，提出了一种新的具有抵抗噪音能力的聚类算 法，称为抗噪音聚类算法.该算法通过将已知数据集划分为非噪音数据集和噪音数据集2个子集，然后对非噪音数 据集进行聚类分析，估计出模型的各个参数.通过对噪音数据集和非噪音数据集进行不断地调整，同时不断地修正 得到的参数估计值，从而得到对聚类结果的优化.实验表明，抗噪音聚类算法能够有效地克服噪音数据对聚类结果 的影响，并估计出优质的参数. 关键词：切换回归模型：聚类：抗噪音聚类算法 中图分类号：1P301.6文献标识码：A文章编号：1673-4785(2009)060497-05 A noise-resistant clustering algorithm for switching regression models YANG Xiao-bing,HE Ling-min',KONG Fan-sheng? (1.Department of Computer Science,China Jiliang University,Hangzhou 310018,China;2.College of Computer Science,Zhejiang University,Hangzhou 310012,China) Abstract:Clustering methods for switching regression models usually neglect the effects of noise.As a result,errors usually exist if clustering is carried out in a noisy environment.In order to overcome the effects of noise,a new clustering algorithm,a noise-resistant clustering algorithm,was proposed.The algorithm partitions the dataset into two sub-datasets,a noiseless dataset and a noisy dataset,and then performs clustering analysis on the noiseless dataset to estimate parameters.By continuous simultaneous adjustment of the noisy and noiseless datasets and by continuously revising estimated parameters,the results of clustering were improved.Simulation experiments demon- strated that the algorithm efficiently clusters noisy datasets and can provide good estimates of parameters. Keywords:switching regression models;clustering;noise-resistant clustering algorithm 聚类分析是当前研究的一个热点，已经广泛地 种特殊的混合分布模型。 应用在模式识别、数据分析、图像处理等许多领域 中.混合分布模型是一种由分别满足多种不同分 1切换回归模型 布规律的数据混合在一起的模型，是统计学中最重 假设S={(x1,y1),…,（x,yn)}是一个数据 要的模型之一，这种模型也已经应用到聚类问题的 集，其中x:∈R°，y.∈R,在最简单的数据回归问题 研究中.由于参数回归往往能够很好地描述数据集 中，假设x和y满足一个简单的函数关系，即 的特征，因此参数回归模型成为对数据集进行聚类 y=fx,β)+e. (1) 分析的一种重要形式.通常要分析的数据集并不是 式中：B∈2CR为待确定的参数向量，e为随机向 满足一个简单的回归模型，而是有多个简单回归模 量，其均值向量为4=0∈R,协方差矩阵为.然 型混合而成的混合回归模型，即切换回归模型 而，在很多情况下，x和y并不是简单地满足函数关 (switching regression models),切换回归模型就是一 系式(1)，而是满足一种更复杂的函数关系： y=f(x;β：)+e,1≤i≤c (2) 收稿日期：200905-11. 基金项目：国家自然科学基金资助项目(60842009). 其中每个参数向量Be2CR:,每个随机向量E:对 通信作者：杨小兵.E-mail:xyang@cjlu.eu.cm. 应的均值向量和协方差矩阵分别为：=0∈R和

·498· 智能系统学报 第4卷 ·基于这种函数关系的模型称为切换回归模型.切 En(U,{B:)= 换回归模型在很多领域尤其是经济领域24]已经得 分∑UgE(B). 名白 (5) 到广泛的应用。 式中：m>1为一个决定结果簇的模糊性的加权指数 一个典型的例子可以用来解释这种模型)，人 FCRM算法通过最小化目标函数族(5)来估计 们在对鱼类的研究中发现，一种大比目鱼有种有趣 每个参数B:和隶属度Uk的值.FCRM算法在无噪 现象，在一定的年龄范围内，雄性的大比目鱼的平均 音的情况下可以广泛应用于切换回归模型的参数估 长度和它的年龄近似地满足一个线性函数关系；同 计和聚类，并能够得到较好的计算结果. 样，雌性的大比目鱼的平均长度和它的年龄近似地 近年来，通过对FCRM算法的研究，一些改进 满足另一个线性函数关系，这2个线性函数关系并 的方法被提了出来，如PPSR算法89)、离群模糊核 不相同.大比目鱼的长度和年龄是可以测量或得到 聚类算法[1o、GFC算法1112]等.这些算法增强了 的，而它们的性别是未知的.对这2个线性函数的参 FCRM算法的功能，扩大了CRM算法的应用范围， 数的确定问题就是一个简单的切换回归问题，这里 然而，它们和FCRM算法一样忽略了噪音数据的干 c=2,s=1,t=1,y为长度，x为年龄，这个切换回归 扰.当数据集中含有噪音数据尤其是大量噪音数据 模型就可以表示为 时，不管是HCM算法还是FCRM算法及其一些改 进方法，都无法排除噪音的干忧，计算结果也因此会 [y=fi(x,B1)+8=Bux+B12+1, (3) 受到影响.由于这些算法没有考虑噪音数据的影响， y=f(x,B2)+62=B2x+B22+62. 把它们统称为无噪音聚类算法(no noise clustering 假设对不同的数据(x,y)和(x,y)来说，E algorithm).为了能够更有效地排除数据集中的噪音 和2的值总是相互独立的，并且分别满足均值为 数据的干扰，提出了一种以无噪音聚类算法为基础， 0,方差分别为01和02的正态分布.目前已经有一 但又与选用何种无噪音聚类算法无关，并且具有抵 些方法对切换回归模型进行参数估计，如硬c-平均 抗噪音能力的聚类算法一抗噪音聚类算法(noise 算法(hard c-means,HCM)[61和模糊c-回归模型算 resistance clustering algorithm,NRC Algorithm). 法(fuz☒c-regression models,FCRM)[71等. 法能够对数据集中存在的大量噪音数据进行清除， 2 已有算法及其存在的缺陷 有效地克服了噪音数据对计算结果的影响，很好地 解决了数据集中的噪音问题， 含有c个回归函数分支的切换回归模型又可称 为c-回归模型.要对c-回归模型的参数进行估计，一 3抗噪音聚类算法 个简单的思路就是，首先将数据集S划分为c个子 在切换回归模型(2)中，为了识别出数据集中 集，然后对每个子集分别进行单模型回归，从而得到 的噪音数据，用du(xk,yk)表示数据点(xk,yk)到y= 每个子函数的参数.这种方法称为硬c-划分法.硬c- f(x;B:)的距离.这里的距离是一个抽象的概念，它 划分法根据划分方法的不同而有多种算法，比如硬 是用来判断数据点(x,y)与y=f(x;B:)的相似程 c-平均算法.这类算法虽然实现起来比较容易，但由 度的标准，例如在二维空间中，它可以用点(xk,y) 于它们没有考虑到各个回归函数分支的重叠的情 到曲线y=f(x;B:)的最近距离表示，也可以用点 况，即没有考虑到数据的模糊性，因此它们的应用存 (xk,y)到曲线y=f(x;B:)中纵坐标与(x,y)相同 在一定的局限性。 的点的距离，即y-f(xk,β：)|表示，可见它是一个 Hathaway和Bezdek在1993年提出了一种模糊 相对的标准.设定一个距离阈值0，当d:(xk,ye)≤ c-回归模型算法「，这种算法在对数据集S进行模 w时，说明与y=(x;B:)之间的距离足够近，可以 糊c-划分的同时估计c-回归模型的参数.对于回归 判断出它不是噪音数据，或者即使它是由于噪音产 模型(1)来说，隶属度(membership degree)Uk(U 生的数据也不会对回归结果产生负面影响，因此可 表示隶属度矩阵U的第i行第k列的值，0≤U≤1 以认为(，y)不是噪音数据；而当(xk,y)对所有 的y=f(x;B)(1≤i≤c)的距离都大于w时，就可 且∑U=1)用来表示模型(；B,)在多大程度 以认为(x,y)是一个噪音数据， 上与y。匹配.误差判定标准可以是各种测量f(xk; 根据以上思想，提出了切换回归模型的抗噪音 B:)与yk之间的误差的方法，最常用的是 聚类(noise resistance clustering algorithm,NRC),算 Ew(B:)=‖f(x;p:)-y‖2 (4) 法的流程图如图1所示. FCRM的目标函数族可以定义为

第6期 杨小兵，等：切换回归模型的抗噪音聚类算法 ·499· 输入数据集 其中的每一个数据点(，y),如果它不是刚从S 中转移过来的，则对0≤i≤c分别计算du(,y). 如果存在某个d(xk,y.)≤w(1≤j≤c),那么就把 模糊划分数据集 (x,y)从S清除，加入到S中. 5)如果Sa和S不再发生变化或者‖B)- 清除噪音数据 B+”‖0.初始化非噪音数据集合 01=0.25,B21=1.0,B2=0和02=0.25.每个数据 S0=S和噪音数据集合S0=0,同时令r=0. 点(xk,y)的生成过程如下： 2)利用无噪音聚类算法对S进行划分回归和 1)按均匀分布随机生成一个数∈(0,1)，如 估计参数，得到各子模型的参数值β及模型y)= 果%0,则把(xk,y)从S 据，否则根据模型(3)，通过x、B和Ba计算y, 清除，加入到S中. 这时的(x,y)为非噪音数据。 4)更新S。→S”:扫描S.中的数据，对于 从数据的生成过程可以看出这个切换回归模型

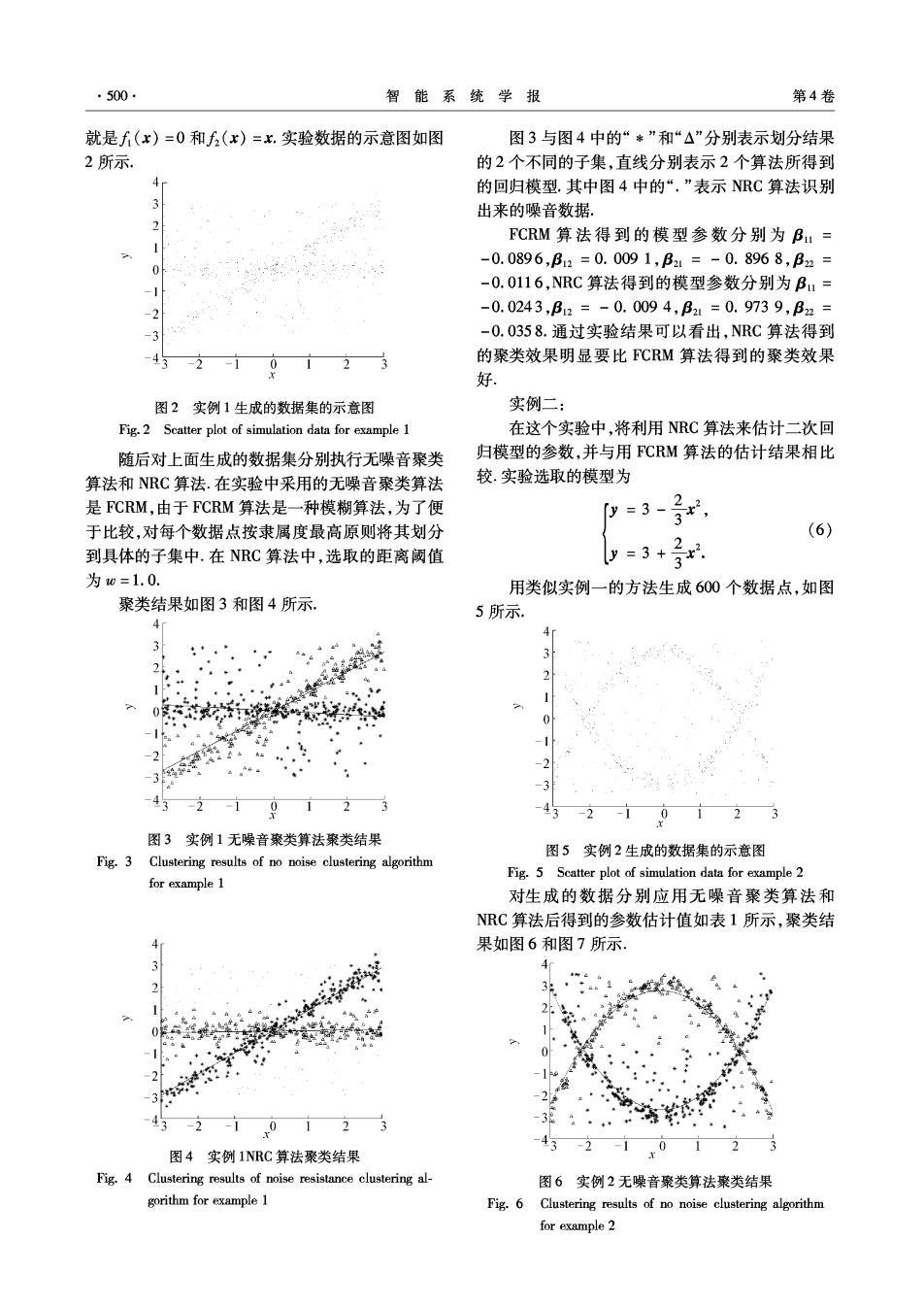
·500· 智能系统学报 第4卷 就是f(x)=0和f(x)=x.实验数据的示意图如图 图3与图4中的“*”和“△”分别表示划分结果 2所示. 的2个不同的子集，直线分别表示2个算法所得到 4 的回归模型.其中图4中的“.”表示NRC算法识别 3 出来的噪音数据。 2 FCRM算法得到的模型参数分别为B:= -0.0896,B12=0.0091,B1=-0.8968,B22= -1H -0.0116,NRC算法得到的模型参数分别为Bu= -2 -0.0243,B2=-0.0094,B21=0.9739,B2= -3 -0.0358.通过实验结果可以看出，NRC算法得到 -2-1 123 的聚类效果明显要比F℃RM算法得到的聚类效果 好 图2实例1生成的数据集的示意图 实例二： Fig.2 Scatter plot of simulation data for example 1 在这个实验中，将利用NRC算法来估计二次回 随后对上面生成的数据集分别执行无噪音聚类 归模型的参数，并与用FCRM算法的估计结果相比 算法和NRC算法.在实验中采用的无噪音聚类算法 较.实验选取的模型为 是FCRM,由于FCRM算法是一种模糊算法，为了便 y 于比较，对每个数据点按隶属度最高原则将其划分 (6) 到具体的子集中.在NRC算法中，选取的距离阈值 y=3+ 为w=1.0. 用类似实例一的方法生成600个数据点，如图 聚类结果如图3和图4所示. 5所示. 4 4 2 2 1 一0 -1 -2 3 2 43-2-10123 43 -2-1 0123 图3实例1无噪音聚类算法聚类结果 图5实例2生成的数据集的示意图 Fig.3 Clustering results of no noise clustering algorithm Fig.5 Scatter plot of simulation data for example 2 for example 1 对生成的数据分别应用无噪音聚类算法和 NRC算法后得到的参数估计值如表1所示，聚类结 4 果如图6和图7所示。 3 3:· 24 1 -1 a 0 24 * -1e -2。 沙 4-210123 图4实例1NRC算法聚类结果 43-2-10123 Fig.4 Clustering results of noise resistance clustering al- 图6实例2无噪音聚类算法聚类结果 gorithm for example 1 Fig.6 Clustering results of no noise clustering algorithm for example 2

第6期 杨小兵，等：切换回归模型的抗噪音聚类算法 ·501· Statist Ass,.1978,73:730-752. 4 [5]HOSMER D W.Maximum likelihood estimates of the pa- 3 rameters of a mixture of two regression lines[J].Communi- 2 cations in Statistics,1974,3(10):995-1005. [6]BEZDEK J C.Pattern recognition with fuzzy objective fune- tion algorithms M].New York:Plenum Press,1981:88- 0 94. -e [7]HATHAWAY R J,BEZDEK J C.Switching regression 2 models and fuzzy clustering[J].IEEE Trans on Fuzzy Sys- -3日 tems,1993,1(3):195-204. [8 ]OHTA T,YAMAKAWA A,ICHIHASHI H,et al.Projec- 0 2 3 tion pursuit switching regression[C]//Proc of 5th Interna- tional Conference on Soft Computing.lizuka,Japan,1998: 图7实例2NRC算法聚类结果 775-778. Fig.7 Clustering results of noise resistance clustering al- [9]OHTA T,YAMAKAWA A,ICHIHASHI H,et al.Projec- gorithm for example 2 tion pursuit switching regression for analysis of psychological feelings[J].Joural of Biomedical Soft Computing and Hu- man Sciences,1998,4(1):15-21. 表1无噪音算法和NRC算法得到的结果比较 [10]沈红斌，王士同，吴小俊.离群模糊核聚类算法[J] Table 1 Results comparison of no noise clustering algo- 软件学报，2004,15(7)：1021-1029. rithm and NRC algorithm SHEN Hongbin,WANG Shitong,WU Xiaojun.Fuzzy ker- B11 B12B3 B21 B22 βa nel clustering with outliers[J].Journal of Software,2004, 15(7):1021-1029. 无噪音聚 2.7346-0.0437-0.5972-2.7067-0.01060.6194 [11]WANG Shitong,JIANG Haifeng,LU Hongjun.A new in- 类算法 tegrated clustering algorithm GFC and switching regression NRC算法2.9335-0.028-0.6521-2.9277-0.01130.602 [J].Intemational Journal of Pattem Recognition and Arti- ficial Intelligence,2002,16(4):433-446. 通过实验结果可以看出，NRC算法明显削弱了 [12]陆宏钧，江海峰，王士同.关于切换回归的集成模糊聚 噪音数据的影响，得到了比无噪音聚类算法更优的 类算法CF℃[J].软件学报，2002,13(10)：1905-1914. 模型参数.实验中0的选择也是很重要的，0选择的 LU Hongjun,JIANG Haifeng,WANG Shitong.An inte- 太大，对噪音的抵抗能力就会减弱，0选择的太小， grated fuzzy clustering algorithm GFC for switching regres- sions[J].Joumal of Software,2002,13 (10):1905 就会将一些非噪音数据误当作噪音数据。 1914. 作者简介： 5结束语 杨小兵，男，1976年生，博士，副教 首先介绍了切换回归模型的基本概念，然后介绍 授，硕士生导师，主要研究方向为数据 了已有的切换回归模型的聚类方法，分析并指出了它 挖掘、知识工程等，发表学术论文10余 们的缺陷：即它们都没有考虑噪音数据对聚类结果的 篇，其中多篇被SCI、EI检索. 影响.在此基础上提出了具有抵抗噪音能力的NRC 算法，并通过仿真实验验证了NRC算法的优越性.实 验上来看，NRC算法是相当成功的，但是仍然有一些 何灵敏，男，1974年生，博士，副教 工作需要做更深入的研究.模型中的子模型个数如何 授，硕士生导师，主要研究方向为数据 确定的问题，距离阈值和的选择以及算法的鲁棒性问 挖掘、机器学习等 题都将是未来研究的重点」 参考文献： [1]HAN Jiawei,KAMBER M.数据挖掘概念与技术[M].范 明，孟小峰，译。北京：机械工业出版社，2001：223-261 孔繁胜，男，1946年生，教授，博士生 [2]HAMERMESH D S.Wage bargains,threshold effects,and 导师，主要研究方向为知识工程、数据挖 the Phillips curve [J].Quarterly Joural of Economics, 掘、人工智能等，获国家科技进步三等奖 1970,84(3):501-517. 1项、省部级科技进步一等奖1项、二等 [3]QUANDT R E.A new approach to estimating switching regres 奖和三等奖各2项，1993年起享受国务 sions[J].J Amer Statist Ass,1972,67(338):306-310. 4]QUANDT R E,RAMSEY J B.Estimating mixtures of nor- 院特殊津贴.在国内外重要刊物上发表 mal distributions and switching regressions[J].J Amer 学术论文30余篇，出版专著3部