智能系统：移动可伸缩三维倒立摆模型的双足机器人步态控制策略

第5卷第1期 智能系统学报 Vol.5 No.1 2010年2月 CAAI Transactions on Intelligent Systems Feh.2010 doi:10.3969/i.issn.1673-4785.2010.01.005 移动可伸缩三维倒立摆模型的 双足机器人步态控制策略 王立权，李恒楠，俞志伟2，韩金华 (1.哈尔滨工程大学机电工程学院，黑龙江哈尔滨150001；2.南京航空航天大学仿生结构与材料防护研究所，江苏 南京210016) 摘要：双足机器人的步态控制策略是保证双足稳定行走的重要条件之一.结合人在行走时ZP平稳移动的特性， 建立了一种移动可伸缩三维倒立摆模型；在约束平面内分析ZP与COG的运动关系，将ZP和COG分别定为快变 因子和慢变因子，提出了移动可伸缩三维倒立摆模型的双足机器人步态控制策略；最后通过Matlab/.ADAMS进行了 步态控制仿真研究.仿真结果表明双足机器人可以稳定地行走，验证了该步态控制策略的可行性。 关键词：双足机器人；三雏倒立摆模型；步态控制策略 中图分类号：TP39文献标识码：A文章编号：16734785(2010)01-0030-05 A gait control strategy of biped robots based on the 3-D inverted pendulum model WANG Li-quan',LI Heng-nan',YU Zhi-wei2,HAN Jin-hua' (1.College of Mechanical and Electrical Engineering,Harbin Engineering University,Harbin 150001,China;2.Institute of Bio-in- spired Structure and Surface Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China) Abstract:Gait control strategies are an important factor affecting the walking stability of bipedal robots.After analy- zing the stable motion of zero moment point (ZMP),we modeled the motion as a scalable 3-D inverted pendulum. The relationship between motion of the ZMP and the center of gravity (CoG)in the constrained plane was ana- lyzed.ZMP was defined as a fast variable,and CoG as a slow variable.With these preconditions,a strategy for controlling bipedal robotic gait could be implemented.It was then simulated using Maltlab/ADAMS.The simula- tion results indicated that this control strategy allows the bipedal robot to walk with good stability,thus verifying the feasibility of the gait control strategy. Keywords:biped robot;3-D inverted pendulum model;gait control strategy 近些年来，国内外仿人双足机器人的技术发展制，规划期望的理想ZP轨迹，通过上身的位置调 迅速，比较著名的仿人双足机器人有日本本田公司 整或上身加速度调整，对ZMP的轨迹进行跟踪控 最新的ASIM0山、索尼公司的QRI02、东京大学的 制[7].第1类控制策略直接跟踪规划后的理想运动 H731、北京理工大学的“汇童”仿人机器人[4.双足 轨迹实现稳定行走，由于缺乏一定的抗干扰能力或 机器人的步态控制策略是保证双足稳定行走的重要 不具有鲁棒性，很难保持稳定行走；第2类控制策略 条件之一.目前，双足机器人步态控制策略主要分为 可以实现行走的步态控制，但桌子的支撑脚相对于 2类：一种是基于ZMP稳定的步态规划或基于倒立 小车的行走范围太小，当小车走向边沿整个系统会 摆模型的步态生成，得到具有稳定性的行走步态轨 失去控制。 迹，然后通过跟踪生成的各关节位置轨迹实现双足 在人的整个行走步态中，零力矩点ZMP(zero mo- 行走56；另一种是基于桌子一小车模型的预观控 ment point)是随支撑区域的变化而移动的，而且双足 机器人重心COG(center of gravity)在空间的运动也 收稿日期：2008-1209 基金项目：哈尔滨工程大学基金资助项目(SJY06028). 是多样的.本文提出一种基于移动可伸缩三维倒立摆 通信作者：李恒楠.E-mail:softli1983@hotmail.com. 模型的双足机器人步态控制策略，通过调整双足机器

第1期 王立权，等：移动可伸缩三维倒立摆模型的双足机器人步态控制策略 ·31 人ZMP位置来跟踪COG位置，并根据伸缩杆的驱动 [x0,yo,],绕X。、Y。和Z。姿态旋转参数为[o,B, 力对双足机器人各关节力矩进行补偿；通过Matlab/. Y]Xo=[y2aoB,Yo],即双足机器人的躯干相 ADAMS进行步态控制策略的仿真研究 对于世界坐标的位姿转换矩阵为 1双足机器人HEUBR1 -CaCp CoSpS,-S.Cy CaSpCy-SaS, x0 SaCe SaSgS,+CaC,SaSpC,-CaS,yo 双足机器人HEUBR_1如图1所示.下肢具有14 -Se CaS, CaC, 20 个自由度，分别为：髋关节3×2个、膝关节1×2个、踝 0 0 0 1J 关节2×2个、足趾关节1×2个.机器人高1.5m,重约 (1) 30kg,表1为HEUBR1的基本设计参数89]」 根据机器人学理论可以建立双足机器人左右腿 髋关节 相邻各关节之间的位姿转换矩阵89]，则各关节相 对于世界坐标的位姿转换矩阵为 T=6T9TT…-T, (2) 膝关节 双足机器人重心表达式： 躁关节感 足趾关节 "Poog= TPm+∑TPma+ΣaTPm m,+∑m:+∑m (3) 图1双足机器人HEUBR1及自由度分配 式中：“P和P分别为左腿和右腿的第i杆件质心 Fig.1 Biped robot of HEUBR_1 and DOF distribution 相对于自身动坐标位置， 表1双足机器人HEUBR1设计参数 Table 1 The parameters of biped robot HEUBR_1 各部名称 长度/m 质量/kg 躯干 0.5 腰部 0.5 6 大腿 0.5 ￥ 小腿 0.5 3 后足 0.2 1.5 前足 0.1 0.5 双足机器人在行走过程中足部与地面时而接触 时而分离，采用支撑腿作为固定世界坐标系时，在行 走过程中通常对步态进行分段分析，使其复杂化，不 利于全局规划. 针对双足行走的特殊性，将双足机器人躯干部 分的坐标作为动坐标系，进而分析双足行走时单腿 图2双足机器人多杆模型 支撑和双腿支撑相互替换运动.相对于地面的世界 Fig.2 Biped robot multi-bar model 坐标系具有在空间的六自由度运动，可假设为躯干 2双足机器人步态控制策略 由固定于地面的6自由度虚拟机械臂操作控制（空 间3自由度移动和3自由度转动)，双足机器人的其 2.1移动可伸缩三维倒立摆模型 他部分相对于躯干的动坐标系通过串联连接.双足 为简化复杂的双足机器人多杆模型，将双足机器 机器人多杆模型如图2所示，1：和l分别为左右腿 人多杆模型简化为单质点模型.由于双足机器人在行 杆件的长度，m和mn分别为左右腿i号杆件的质 走时实际ZMP在水平地面内移动，且C0G与ZMP之 量，L和l分别为左右腿i杆件的相对重心位置，0： 间也存在位置变化，采用一种移动可伸缩倒立摆三维 和0分别为左右腿i杆件与i-1杆之间相对于初 模型作为双足机器人的简化模型，如图3所示.倒立摆 始站立状态下的关节转角. 的质心为双足机器人COG,倒立摆的支撑点为ZP,支 世界坐标系为Σ。，在双足机器人躯干的动坐标 撑点可在水平面内移动，且伸缩杆可在三维空间内可 系为Σ。，动坐标系为Σ。相对于Σ。的空间位置为 伸缩摆动，模拟C0G与△P的位置变化，简化后更方

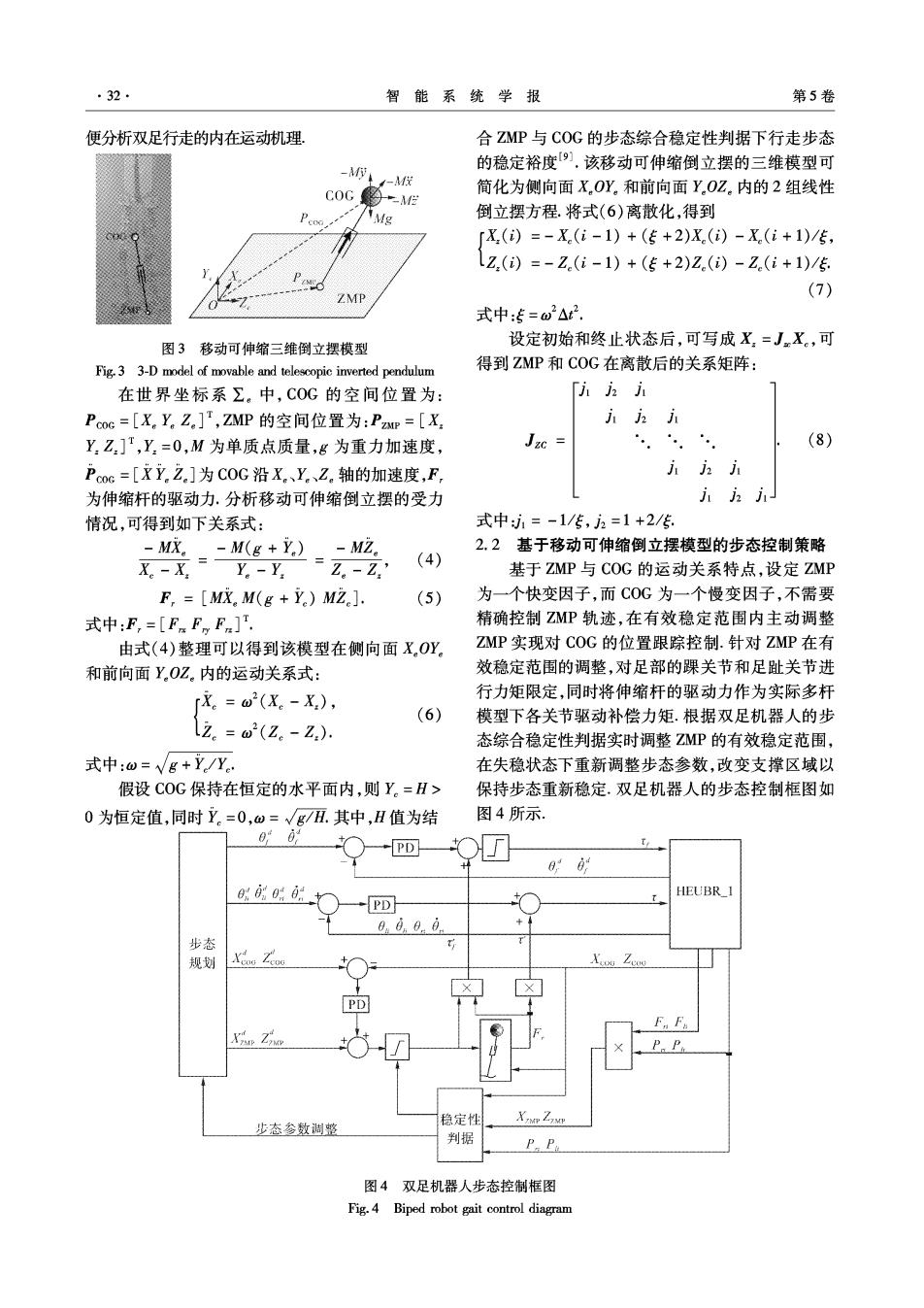
32 智能系统学报 第5卷 便分析双足行走的内在运动机理 合ZMP与COG的步态综合稳定性判据下行走步态 -M生-M 的稳定裕度9).该移动可伸缩倒立摆的三维模型可 C0G-M 简化为侧向面XOY。和前向面YOZ。内的2组线性 1Mg 倒立摆方程.将式(6)离散化，得到 X()=-X.(i-1)+(传+2)X.(i)-X(i+1)/传， lZ.()=-Z.(i-1)+(传+2)Z.(i)-Z.(i+1)/传 (7) ZMP 式中：5=w2△2 图3移动可伸缩三维倒立摆模型 设定初始和终止状态后，可写成X,=JX。,可 Fig.3 3-D model of movable and telescopic inverted pendulum 得到ZMP和COG在离散后的关系矩阵： 在世界坐标系Σ。中，C0G的空间位置为： Pcoc=[XY.Z]T,Z△MP的空间位置为：Pam=[X YZ],Y.=0,M为单质点质量，g为重力加速度， (8) Pcoc=[XY.Z.]为C0G沿X。、Y.、Z。轴的加速度，F 为伸缩杆的驱动力，分析移动可伸缩倒立摆的受力 情况，可得到如下关系式： 式中：i=-1/传，2=1+2/5 -MR。-M(g+Y)-M2。 2.2基于移动可伸缩倒立摆模型的步态控制策略 X.-X=Y.-Y. =Z。-Z' (4) 基于ZMP与COG的运动关系特点，设定ZMP F,=[MX。M(g+Ye)MZ.]. (5) 为一个快变因子，而C0G为一个慢变因子，不需要 式中：E,=[FnFn F] 精确控制ZMP轨迹，在有效稳定范围内主动调整 由式(4)整理可以得到该模型在侧向面X.OY。 Z△MP实现对COG的位置跟踪控制.针对ZMP在有 和前向面YOZ。内的运动关系式： 效稳定范围的调整，对足部的踝关节和足趾关节进 rx。=w2(X。-X), 行力矩限定，同时将伸缩杆的驱动力作为实际多杆 (6) 模型下各关节驱动补偿力矩.根据双足机器人的步 lz=w2(Z。-Z). 态综合稳定性判据实时调整ZMP的有效稳定范围， 式中：w=√g+Y/Yc 在失稳状态下重新调整步态参数，改变支撑区域以 假设COG保持在恒定的水平面内，则Y。=H> 保持步态重新稳定.双足机器人的步态控制框图如 0为恒定值，同时立=0，w=√g/五.其中，H值为结 图4所示， 00 -PD 00站 HEUBR_1 PD 0.0n0.0. 步态 规划 PD P 稳定性 态参数调整 判据 PP 图4双足机器人步态控制框图 Fig.4 Biped robot gait control diagram

第1期 王立权，等：移动可伸缩三维倒立摆模型的双足机器人步态控制策略 ·33· 结合离线规划的拟人稳定行走的步态数据（包括 动仿真中信息传输： 各关节角度和角速度、COG轨迹、ZMP轨迹等)作为 控制的目标数据，通过对关节PD位置跟踪和移动可 伸缩倒立摆伸缩杆驱动力在各关节上的力矩补偿，同 时对足部的踝关节和足趾关节进行力矩限定，防止出 现足底发生倾覆，基于双足机器人反馈的足底压力信 号检测ZMP/COP位置及支撑区域，结合稳定性判据 对ZP有效区域限定，通过对足底ZP的位置调 整，实现对双足机器人COG的稳定跟踪，根据C0G 的跟踪状况，当基于稳定性判据表明双足机器人处于 图5双足机器人的ADAMS仿真模型 不稳定状态时，采用改变规划步态的参数实现对支撑 Fig.5 Biped robot ADAMS Simulation model 面的改变，使双足机器人再次保持稳定 定义了足底面各个接触点与地面的接触力参 对ZMP的位置采用PD调整，并做了上下值限 数，如图6所示，使双足机器人与地面接触时具有较 定，如式(9)和(10)所示： 为稳定的接触力和足够的静摩擦力，较好地模拟了 X=X-kr(X。-X)-kr(X。-),(9) 实际双足机器人行走时与平整地面接触碰撞的特 Z.=Z-krz(Z。-Z)-kz(2。-2).(10) 性.通过步态控制，在地面上完成了步态在步幅为 式中：kpx和kz分别为X和Z方向的比例增益，kox 0.2m下的拟人行走，调整参数krx=1.5、kx=1、 和kz分别为X和Z方向的微分增益，x、Xmn、 krz=1.0、kz=0.5、H=0.85m、dmm=0.02m、km= Z:min和Z:m分别为支撑区域前后左右的极值， k=100、km=k贴=5.从双足机器人行走过程中的 X:min <X<Xm min<<Z:mt 步态侧向面和前向面的运动截图，如图7所示，可以 基于移动可伸缩倒立摆的伸缩杆的驱动力： 看出双足机器人可以稳定行走， F,=[Mg(X。-X)/H MgMg(Z。-Z)/H] 10E40 (11) Force Exponen 22 对各个关节进行力矩补偿的PD关节位置控制： Demping 1.0004 「tn=km0a-knpn+F,×(Pm-[X.0Z]), Fenchstion Dcpth 10正00 ,,,.,,词 Fricion Force Ta=kOa-kpu+F,×（Pa-[X0Z]T). Cauknb Fncbion (12) 03 式中：on=（0n-);pn=(0m-片)；o4=(0a- 02 Sicion Tiarsion Vol );P:=(0:-);T和T:分别对应的右腿和左腿 10 的第关节驱动力矩，和分别为右腿和左腿第 关节的控制角度值，片和分别为右腿和左腿第i 图6 ADAMS中足底力参数设定 关节的控制角速度值，P和P:分别为右腿和左腿 Fig.6 The foot pressure parameter setting in ADAMS 第关节转动轴位置向量： 3 仿真模型及仿真分析 在步态控制的仿真中，必须针对与实际双足机 器人HEUBR1相一致的仿真对象，为此在ADAMS 仿真环境中建立了详尽的双足机器人HEUBR_1的 多杆模型，如图5所示，各杆件的尺寸、质量参数通 过在Pro/E零件建模后导入ADAMS中装配，即建 立了与实际双足机器人的尺寸、质量、传动方式相一 (a)侧面内行走步态 (b)前向面行走步态 致的虚拟样机模型9).为增加步态控制实现的可行 图7双足机器人行走步态 性，在Matlab/SimMechanics中搭建控制模块，结合 Fig.7 Biped robot walking gait 离散规划的拟人稳定行走的步态数据（包括各关节 如图8双足机器人COG运动轨迹可知，在该 角度和角速度、COG轨迹、ZMP轨迹等)作为控制的 步态方式下行走中给定的COG轨迹，与实际COG 目标数据，通过ADAMS/Controls接口模块链接2种 运动仿真结果的总体运动趋势相一致，实际COG轨 软件，实现Matlab中控制算法输出和ADAMS中运 迹与给定轨迹相比欠光滑，但仍能保证C0G在空间

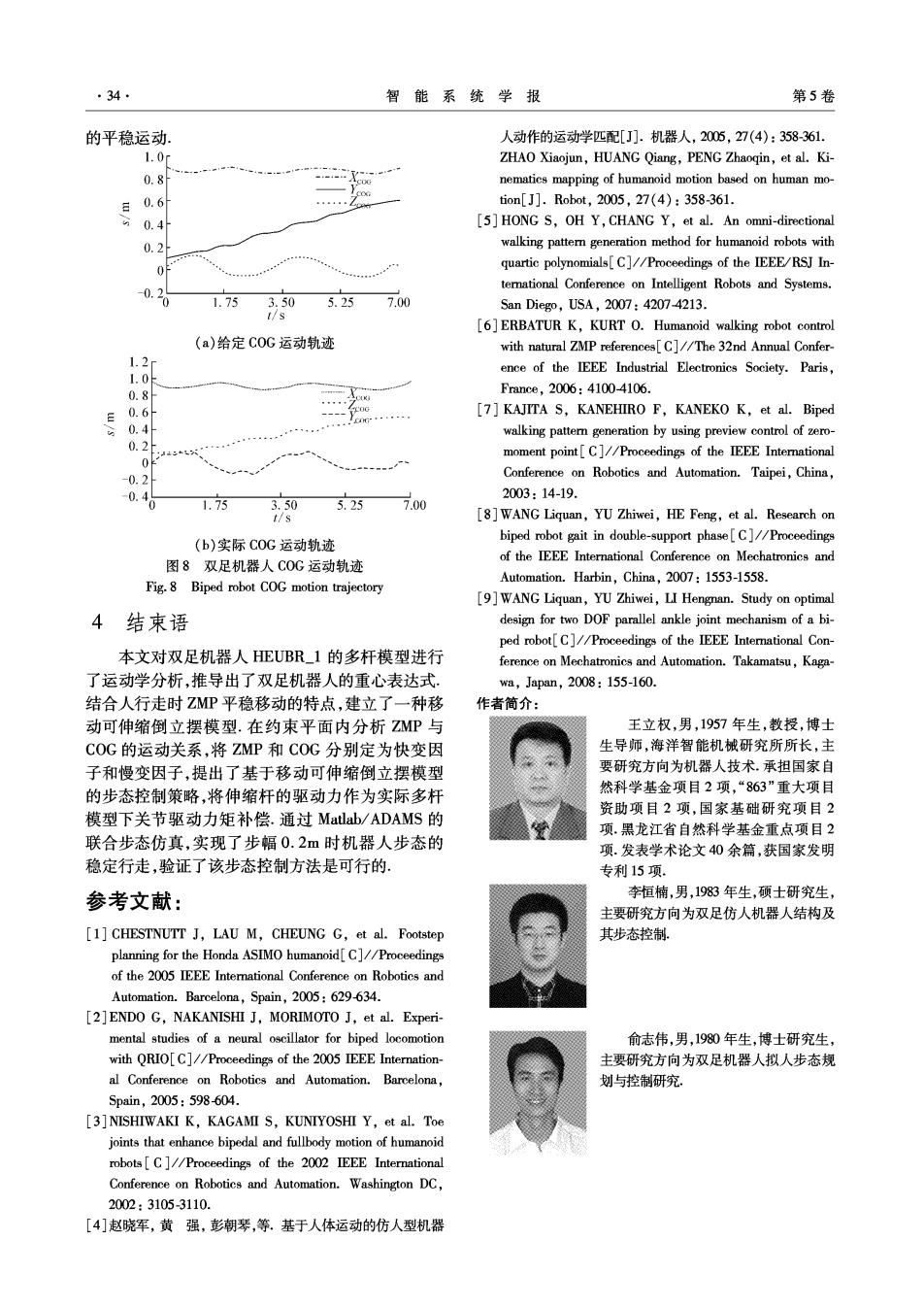
·34 智能系统学报 第5卷 的平稳运动， 人动作的运动学匹配[J】.机器人，2005,27(4)：358-361. 1.0m ZHAO Xiaojun,HUANG Qiang,PENG Zhaoqin,et al.Ki- 0.8 nematics mapping of humanoid motion based on human mo- 0.6 tion[J].Robot,2005,27(4):358-361. 0.4 [5]HONG S,OH Y,CHANG Y,et al.An omni-directional 0.2 walking patter generation method for humanoid robots with quartic polynomials[C]//Proceedings of the IEEE/RSJ In- temational Conference on Intelligent Robots and Systems. 1.75 3.50 5.25 7.00 San Diege0,USA,2007:4207-4213. [6]ERBATUR K,KURT O.Humanoid walking robot control (a)给定C0G运动轨迹 with natural ZMP references[C]//The 32nd Annual Confer- ence of the IEEE Industrial Electronics Society.Paris, 1.0 0.8 France,2006:4100-4106. LOG E 0.6 [7]KAJITA S,KANEHIRO F,KANEKO K,et al.Biped 0.4 walking pattern generation by using preview control of zero- 0.2 0 moment point[C]//Proceedings of the IEEE International -0.2 Conference on Robotics and Automation.Taipei,China, -0.4 2003:14-19. 1.73 3.50 5.25 7.00 t/s [8]WANG Liquan,YU Zhiwei,HE Feng,et al.Research on (b)实际COG运动轨迹 biped robot gait in double-support phase[C]//Proceedings 图8双足机器人COG运动轨迹 of the IEEE International Conference on Mechatronics and Fig.8 Biped robot COG motion trajectory Automation.Harbin,China,2007:1553-1558. [9]WANG Liquan,YU Zhiwei,LI Hengnan.Study on optimal 4 结束语 design for two DOF parallel ankle joint mechanism of a bi- ped robot[C]//Proceedings of the IEEE International Con- 本文对双足机器人HEUBR_1的多杆模型进行 ference on Mechatronics and Automation.Takamatsu,Kaga- 了运动学分析，推导出了双足机器人的重心表达式. wa,Japan,2008:155-160. 结合人行走时ZMP平稳移动的特点，建立了一种移 作者简介： 动可伸缩倒立摆模型.在约束平面内分析ZMP与 王立权，男，1957年生，教授，博士 COG的运动关系，将ZMP和COG分别定为快变因 生导师，海洋智能机械研究所所长，主 子和慢变因子，提出了基于移动可伸缩倒立摆模型 要研究方向为机器人技术.承担国家自 的步态控制策略，将伸缩杆的驱动力作为实际多杆 然科学基金项目2项，“863”重大项目 模型下关节驱动力矩补偿.通过Matlab/ADAMS的 资助项目2项，国家基础研究项目2 项.黑龙江省自然科学基金重点项目2 联合步态仿真，实现了步幅0.2m时机器人步态的 项.发表学术论文40余篇，获国家发明 稳定行走，验证了该步态控制方法是可行的， 专利15项. 参考文献： 李恒楠，男，1983年生，硕士研究生， 主要研究方向为双足仿人机器人结构及 [1]CHESTNUTT J,LAU M,CHEUNG G,et al.Footstep 其步态控制。 planning for the Honda ASIMO humanoid[C]//Proceedings of the 2005 IEEE Intemational Conference on Robotics and Automation.Barcelona,Spain,2005:629-634. 2]ENDO G,NAKANISHI J,MORIMOTO J,et al.Experi- mental studies of a neural oscillator for biped locomotion 俞志伟，男，1980年生，博士研究生， with QRIO[C]//Proceedings of the 2005 IEEE Internation- 主要研究方向为双足机器人拟人步态规 al Conference on Robotics and Automation.Barcelona, 划与控制研究。 Spain,2005:598-604. [3]NISHIWAKI K,KAGAMI S,KUNIYOSHI Y,et al.Toe joints that enhance bipedal and fullbody motion of humanoid robots[C]//Proceedings of the 2002 IEEE International Conference on Robotics and Automation.Washington DC, 2002:3105-3110. [4]赵晓军，黄强，彭朝琴，等。基于人体运动的仿人型机器