智能系统：二足机器人之动态平衡研究

第4卷第5期 智能系统学报 VoL.4 No.5 2009年10月 CAAI Transactions on Intelligent Systems 0ct.2009 doi:10.3969/j.issn.16734785.2009.05.013 二足机器人之动态平衡研究 王仲淳，倪世铨，黄加庆，李明哲，郑晖腾，郭怡均 (元智大学电机系，台湾中扬32003) 摘要：主要探讨二足机器人(biped robots)行走或受到外力干扰时，通过动态平衡控制使机器人行走更趋稳定，并 增强站立时稳定性.二足机器人动态平衡之实现，主要是将动态平衡控制程序撰写于N0sⅡ发展环境中，当二足机 器人行走时，利用脚底压力传感器取得压力值，运算及判断二足机器人实际重心是否落在二足机器人支撑多边形范 围内，并计算实际重心与期望重心之误差，以模糊控制器将二足机器人重心控制于支撑多边形范围内，使二足机器 人行走时能够更加稳定，实验结果表明该方法是有效的， 关键词：二足机器人；动态平衡控制；模糊控制器 中图分类号：TP242文献标识码：A文章编号：16734785(2009)05046308 Dynamic balance for bipedal robots WANG Jong-chwen,NI Shih-chiuan,HUANG Chia-ching,LI Ming-che,CHENG Hui-teng,KUO Yi-chun (Department of Electrical Engineering,Yuan Ze University,Chung-Li 32003,China) Abstract:The main purpose of this paper was to study how to enhance the dynamic balance of bipedal robots dur- ing walking or when interacting with external forces.Their stability while standing was also examined.The dynamic equilibrium of the tested biped robots resulted from built-in dynamic control programs which were written in the Nios development environment.To get pressure values from the pressure sensors of biped robots,we used control algo- rithms to compute the position of the actual center of gravity (CoG)and also to determine whether the CoG fell in- side the polygon defining the area of balance for the robot.It was found possible to use a fuzzy controller to compen- sate for errors due to differences between the actual CoG and the theoretical one.The objective was to keep the CoG within the supporting polygon area.This helped the bipedal robots walk more steadily and also improved their over- all stability when standing.The experimental results show that this method is effective. Keywords:biped robot;dynamic state control;fuzzy control 随着科技的进步，世界各国渐渐开始投入机器 本文主要研究二足机器人的动态平衡，当机器 人领域的研究.机器人有很多不同类型，像是水下机 人运行时，经由传感器取值并通过控制器补偿机器 器人、飞行机器人、地下机器人等.不论是何种类型 人重心稳定位置，分析比较不同控制器的性能差异， 机器人大致上都可以分为轮型、多足型和轨道式等， 让机器人不论在静态或动态状态下都能够具有抗干 其中又以最像人类的二足机器人(biped robots)最 扰性能，使得机器人在姿态及运作效能上有所改善. 受世人瞩目 1二足机器人硬件架构 目前二足机器人步行还无法像人类一样，来去 自如行走于不同的地形上，而且人类步行时本身因1.1硬件架构 为拥有平衡功能，所以步行时才不至于跌倒，目前二 如图1所示为二足机器人正面及侧面图，该二 足机器人步行时最需克服的就是平衡问题.二足机 足机器人是由双足10个自由度、头部1个自由度、 器人克服地形限制后，即可代替人类于危险环境或 FPGA发展实验板、伺服机驱动模块、无线模块、超 是人类无法到达的地方执行各种任务. 音波传感器、电子罗盘、加速度计以及8颗压力传感 收稿日期：200903-12. 器所架构出的.二足机器人站立时高为320mm,宽 通信作者：郭怡均.E-mail:goldber6@yahoo.com.tw. 为230mm,重量约1.5kg,脚底是A/D转换电路及

·464 智能系统学报 第4卷 8颗压力传感器组合，大小为6cm×9cm. (Microsoft foundation classes)架构建立了监控画面， 时 以利能够在桌上型计算机(desktop)上监控二足机 器人各个传感器取值的情况.如图4所示为压力监 控画面。 图1二足机器人正面及侧面图 Fig.1 The biped robot 该二足机器人主要是藉由脚底压力传感器取值 图4脚底压力监控画面 并运算出实际重心位置后，并控制伺服机以达到行 Fig.4 Foot pressure monitoring screen 走平衡的目的.本文所使用的压力传感器为 1.2.1平衡架构 FSR400,如图2所示.SR400是一种整体体积小且 二足机器人步行时，平衡控制重心的偏移分为 能够连续检测压力强弱的电阻式压力传感器. 双脚与单脚2种情况，如图5所示为二足机器人 双脚控制流程， 机器人一 单與粹制 双翠 控制 单解控制 图5二足机器人双脚控制流程 Fig.5 Biped robot legs control flow 图2SR400压力传感器实体图 如图6所示为二足机器人脚底坐标系统，二足 Fig.2 FSR400 pressure sensor entity chart 机器人重心位置偏移分为X、Y2种不同方向，经由 由于压力传感器输出为模拟信号，为了使得 此2种不同方向判断出实际重心位置，当二足机器 FPGA发展实验板取得压力值，故透过IC设计出AV 人步行时往前为-X方向，往后为+X方向，而往左 D转换电路.为了节省空间，故将A/D转换电路制 倾时为一Y方向，往右倾则为+Y方向。 作于二足机器人脚底，如图3所示为二足机器人脚 桑X灯后) 底实体图 -Y左} (右) 压力感测器 -x灯前) 图3二足机器人脚底实体图 图6二足机器人脚底坐标系统 Fig.3 The biped robot sole physical map Fig.6 Biped robot foot coordinate system 1.2软件架构 本文平衡架构分为压力传感器初始化、压力传 本研究的目的是实现二足机器人的动态平衡， 感器取得压力值、压力值滤波、重心误差、平衡控制 主要通过程序撰写于FPGA发展实验板中.为了能 及伺服机补偿等6个架构，通过这6部分规划出整 够方便测试与监控整个机器人状态，使用VC6.0 个二足机器人步行平衡控制流程，如图7所示. (Microsoft visual C+6.0)开发环境，并利用MFC

第5期 王仲淳，等：二足机器人之动态平衡研究 ·465· 府动 压力感测器 初始化 压力感测发 读取压力值 压力值滤波 计算压力重心 -1 期望重心 重心误差 判断重心位置 Error=0 Y方向 X方向 Error=0 t上rror≠0 rror≠0 平衡控制器 平衡控制器 单脚支持 单脚支持 相位 相位 单或双脚 单或双脚 者地 若地 双脚支持 双脚支持 左 神位 左脚或右脚 左 左脚或h脚 相位 者地 着地 五 补偿左脚腹新 补偿右脚腹部 补偿双脚腹部 补偿左脚 补偿右脚 补偿双脚 及脚躁角度 及脚踩角度 及脚蹀角度 膝盖角度 膝盖角度 膝盖角度 主控端足不停止 Y 结束 图7步态平衡流程图 Fig.7 The flow chart of walk-state balance 1.2.2压力传感器初始化 1.2.3计算压力值 图8所示为压力值初始化流程图.二足机器人 二足机器人运行时，压力传感器受力后其电阻 站立时的重量对地面有一定作用力，所以二足机器 值随之改变，经由AVD电路转换成PWM信号，透过 人启动前会将压力传感器初始化，其用意为取得二 FPGA实验板运算PWM由低电位到高电位脉波数 足机器人站立时初始状态压力值，并排除机器人本 量，从而取得各个压力传感器的实际压力值，如图9 身震动之干扰，避免二足机器人平衡系统误判。 所示为取得压力值流程图.PCA实验板运算后各 个压力传感器压力值的范围为0~4000个脉冲

·466· 智能系统学报 第4卷 开始 d() 0.2 二足机器人运行 Input- -du-1) 爪力感测器取爪力值一 -2→ 压力值加总求基准俏 图10数字滤波器 Fig.10 Digital filter 取值是否达到10还 N 1.2.5计算重心及平衡控制 Y 二足机器人移动时会有一个实际重心位置，实 一压力感测器取压力值 际重心分为X、Y2个不同方向，二足机器人运动时 每一个动作都会对应一个理论重心位置，将实际重 平衡系统 心与期望重心相减后得到一组重心误差值，此误差 值是平衡控制的主要依据.将重心的误差值通过控 主端是否停止一 制器运算，运算出伺服机补偿角度，藉由此角度补偿 Y 所对应的伺服机，来补偿误差的影响，使二足机器人 结束) 行走时能更加顺畅稳定，并让机器人能够拥有抗干 图8压力传感器初始化流程图 扰的功能，如图11所示. Fig.8 Pressure sensor initialization flowchart X方向误差值 X方向补偿伯 开始 控制器 二足机器人运行 方向误差值 Y方向补偿值 压力感测器取初始化 图11补偿值运算流程图 Fig.11 The flow chart of compensation value operation 压力感测器感受压力+ 2平衡控制理论 AD电路产生Pulse 2.1零力矩点 PGA计算ls数量 零力矩点(zero moment point,ZMP)是由Vuko bratvic于1968年提出[3].如图12所示为脚底反作 取得压力值 用力情形，二足机器人接触地面时，若将地面的反作 用力集中一点P,会有集中力(counterforce)N及力 半衡控制系统 矩M产生，此时P点周围的惯性力及重力产生的净 力矩和为零，即称P点为零力矩点. 主控端是停止 Y 结束 ZMP 图9取得压力值流程图 Fig.9 The flow chart of pressure value obtaining 1.2.4压力值滤波 二足机器人运行时机身晃动将产生突波，因此 藉由滤波器降低突波干扰.本文采用的滤波方法是 图12脚底反作用力情形 将各个压力传感器当次取得的压力值与前1次及前 Fig.12 Foot reaction force 2次所取得的压力值分别乘一定得倍率后加总而 二足机器人运动时本身各连杆会产生加速度而 成.如图10所示为数字滤波器，d(t)为当前所取到 具有惯性力.假设机器人本身全部连杆、力矩与地面 的压力值、d(t-1)为前1次所取到的压力值、d(t- 反作用力相互抵消，即二足机器人所有杆件合力作 2)为前2次所取到的压力值 用于二足机器人支撑多边形（脚掌）内，此时二足机

第5期 王仲淳，等：二足机器人之动态平衡研究 ·467· 器人则保持稳定不倾倒；反之若二足机器人合力作 用于支撑多边形外，二足机器人则会有产生倾倒状 况发生，如图13所示， {xny）,⊙ (x2ys () 左脚单脚支撑面 . 图14压力传感器位置图 Fig.14 Pressure sensor location 右脚单脚支撑向 2.2模糊控制器 本文还要设计一模糊控制器，并由模糊控制器 图13二足机器人步行时ZMP的稳定范围 运算出各伺服机所需的补偿角度.如图15所示为模 Fig.13 Biped robot walking stability of the scope of ZMP 糊控制器补偿流程，将二足机器人期望重心h。与实 际重心位置e,相加减会得到位置误差e,误差e通 通过机器人机身各连杆的关系可求得零力矩点 过模糊控制器运算得到各个伺服机补偿角度9，经 位置，其公式如式(1)所示[3)： 由所对应伺服机将补偿角度日作补偿，让二足机器 ∑(mx8-(m:(元-x)+0y）） 人在站立或步行时达到平衡， h,e+模糊制器 二足机器人 饲服机 mg ∑m: 实际重心、压力感测器 ,(my8-(m:(-y:)+ù)) 图15模糊控制器补偿流程 Fig.15 Fuzzy controller compensation process 补偿方向分为X、Y2个方向，所以X方向及Y (1) 方向的前件部分别为重心误差△x、△y,重心误差变 式中：(xmym,0)为零力矩点的坐标位置；m为总 化量△、△y,后件部为二足机器人双脚伺服机补偿 质量；g为重心的加速度；m:为第i个连杆的质量； 角度大小“、出，·X方向补偿角度向机器人前方“ (x:,y:,)为第i个连杆的质心位置；（无，少，）为第 为负，向后4.为正，Y方向补偿角度向右“，为正，向 i个连杆的质心位置加速度；o、⊙为第i连杆X、Y 左“，为负.前件部模糊集合为5个，后件部模糊集 轴角加速度， 合为7个.△x、△y可以取EM(误差负大)、ES(误差 Vukobratvic也说明若二足机器人运动时所有杆 负小)、EZ(误差零)、EL(误差正小)、EB(误差正 件合力作用于支撑多边形内，压力中心与零力矩点 大)，△、△y可以取DS(差量负大)、DY(差量负 的位置是同一个点，则零力矩点与重心关系可以通 小)、DZ(差量零)、DB(差量正小)、DL(差量正大)， 过二足机器人脚底压力传感器与地面反用力反馈计 山“，其值为ML(补偿负大)MM(补偿负中)、MS 算出二足机器人实际零力矩点位置[45].实际重心 (补偿负小)、Z0(补偿零)、PS(补偿正小)、PM(补 位置可由式(2)求得： 偿正中)和L(补偿正大) ∑xf 经由前件部与后件部的对应并定义出X、Y方 X gp 向的模糊集合如图16~21所示 ∑f =1 (2) -40 -20 0 20 40 式中：f为地面的反作用力；(x:,少：)为压力传感器坐 图16△x归属函数 标位置.图14所示为压力传感器位置图. Fig.16 Ax membership functions

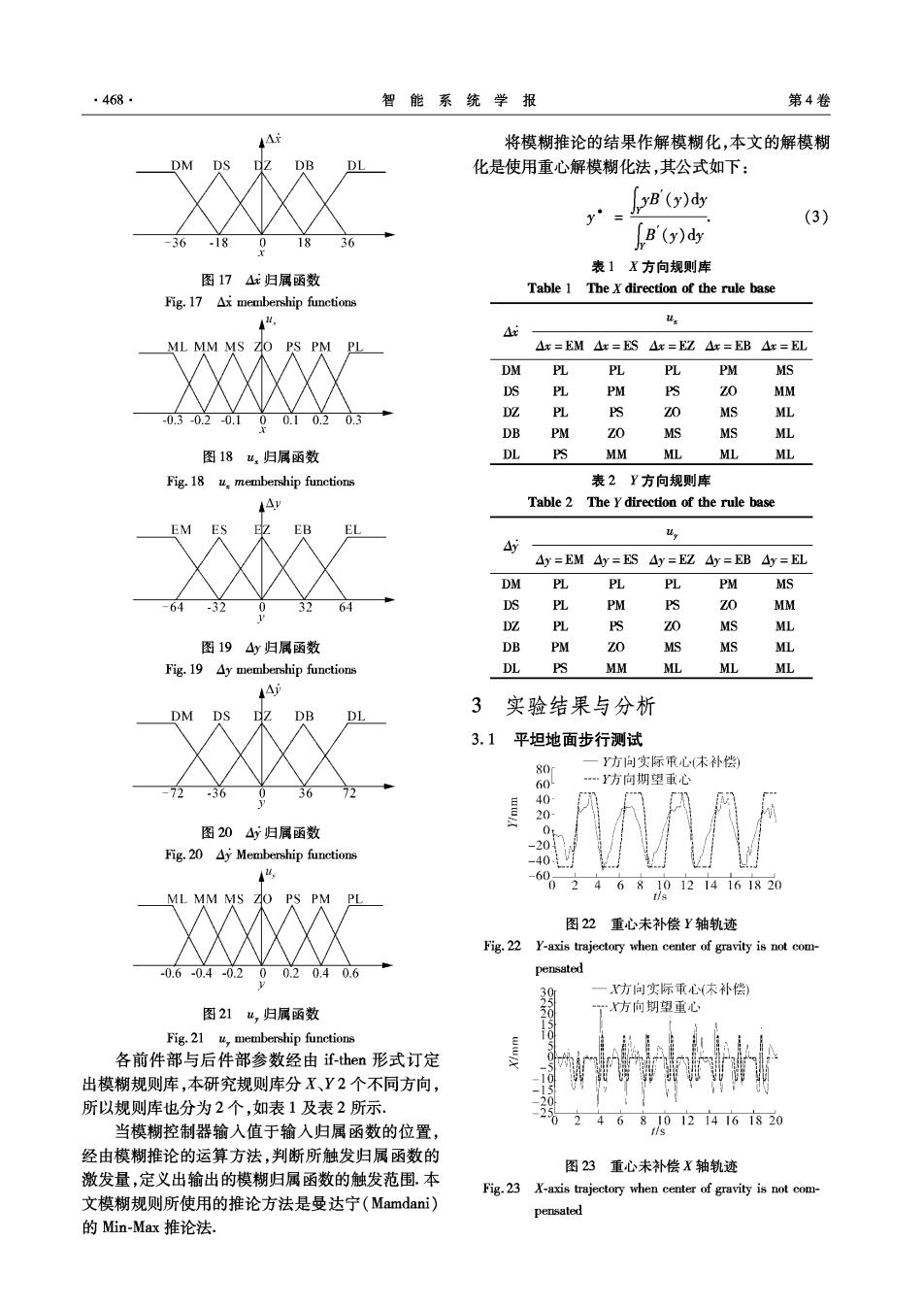
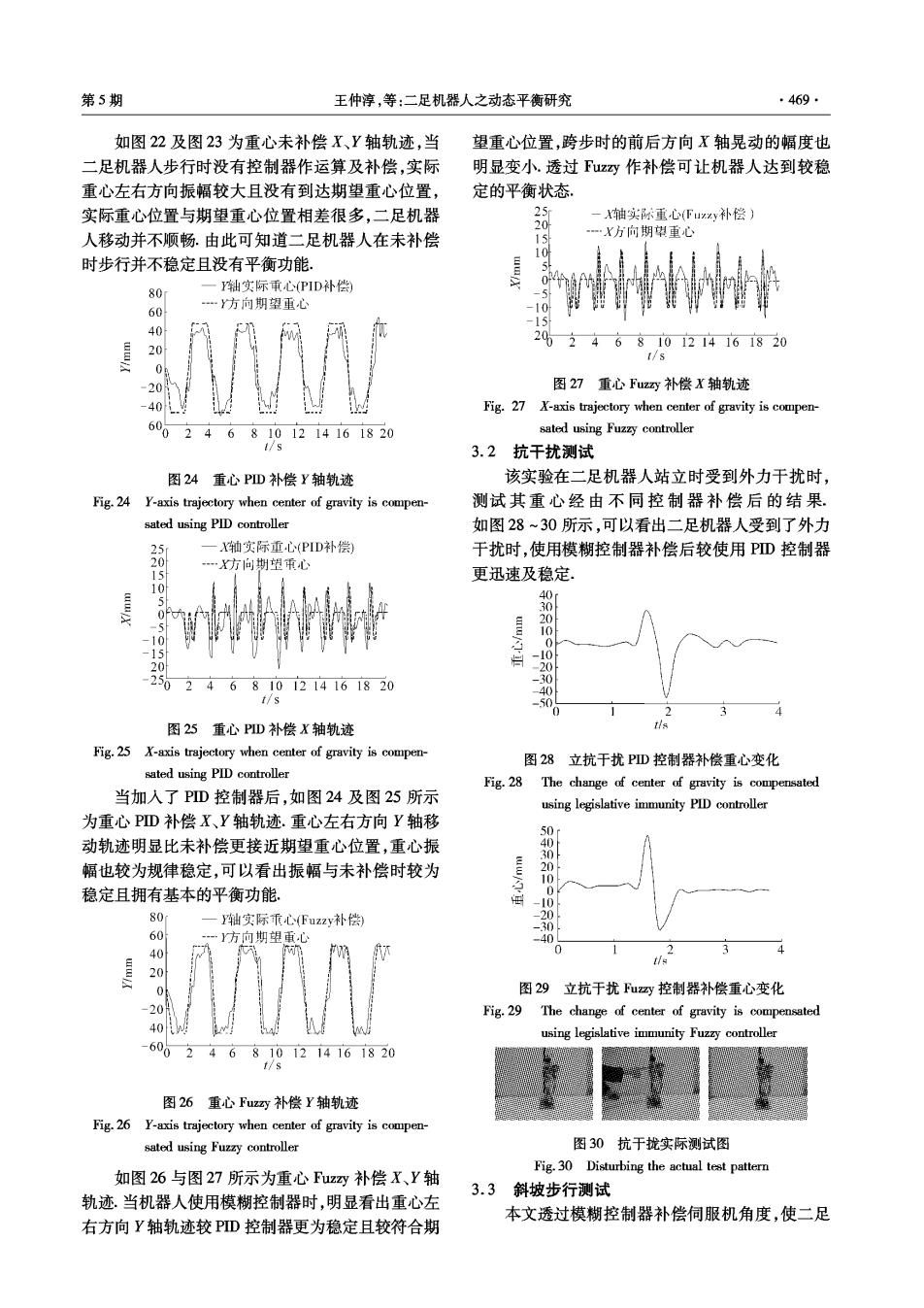
·468· 智能系统学报 第4卷 将模糊推论的结果作解模糊化，本文的解模糊 DM DS 化是使用重心解模糊化法，其公式如下： pB'(y)d (3) 36 -18 18 36 [B'(y)dy 表1X方向规则库 图17△x归属函数 Table 1 The X direction of the rule base Fig.17 Ax membership functions △ ML MM MS ZO PS PM PL △x=EM△x=ES△x=EZ△x=EB△x=EL DM PL PL PL PM MS DS PL PM PS Zo MM -0.3-0.2-0.100.10.20.3 DZ PL PS ZO MS ML DB PM ZO MS MS ML 图18私，归属函数 DL PS MM ML ML ML Fig.18 u.membership functions 表2Y方向规则库 14 Table 2 The Y direction of the rule base EM ES 4 Ay Ay=EM Ay=ES Ay=EZ Ay=EB Ay=EL DM PL PL PL PM MS 64 -32 0 32 DS PL PM PS Zo MM DZ PL PS ZO MS ML 图194y归属函数 DB PM Zo MS MS ML Fig.19 Ay membership functions DL PS MM ML ML ML DM DS DZ DB DL 3实验结果与分析 3.1平坦地面步行测试 了方向实际承心未补偿) 8 60 …Y方向期望重心 40 20 图204y归属函数 0 -20 Fig.20 Ay Membership functions 40明 -6 0 468101214161820 ML MM MS ZO PS PM PL 图22重心未补偿Y轴轨迹 Fig.22 Y-axis trajectory when center of gravity is not com- -0.6-0.4-0.200.20.40.6 pensated 30 一X方问实际重心（木补偿） 图214，归属函数 一X方向期望重心 20 Fig.21 membership functions 各前件部与后件部参数经由f-hen形式订定 出模糊规则库，本研究规则库分X、Y2个不同方向， 所以规则库也分为2个，如表1及表2所示. 当模糊控制器输入值于输入归属函数的位置， 2468,012416i820 经由模糊推论的运算方法，判断所触发归属函数的 图23重心未补偿X轴轨迹 激发量，定义出输出的模糊归属函数的触发范围。本 Fig.23 X-axis trajectory when center of gravity is not com- 文模糊规则所使用的推论方法是曼达宁(Mamdani) pensated 的Min-Max推论法

第5期 王仲淳，等：二足机器人之动态平衡研究 ·469· 如图22及图23为重心未补偿X、Y轴轨迹，当 望重心位置，跨步时的前后方向X轴晃动的幅度也 二足机器人步行时没有控制器作运算及补偿，实际 明显变小.透过Fuz四y作补偿可让机器人达到较稳 重心左右方向振幅较大且没有到达期望重心位置， 定的平衡状态。 实际重心位置与期望重心位置相差很多，二足机器 25 一轴实际重心(Fuy补偿) 2 人移动并不顺畅.由此可知道二足机器人在未补偿 15 …X万向期望重心 10 4 时步行并不稳定且没有平衡功能， 一轴实际重心PID补偿 80 -5 方向期望重心 60 -10 -1 40 30 2062468101214161820 /8 30 图27重心Fuz西补偿X轴轨迹 40 Fig.27 X-axis trajectory when center of gravity is compen- 60024 6 8101214161820 sated using Fuzzy controller 1/s 3.2抗干扰测试 图24重心PD补偿Y轴轨迹 该实验在二足机器人站立时受到外力干扰时， Fig.24 Y-axis trajectory when center of gravity is compen- 测试其重心经由不同控制器补偿后的结果. sated using PID controller 如图28~30所示，可以看出二足机器人受到了外力 25 一X轴实际重心(PID补偿) 干扰时，使用模糊控制器补偿后较使用PD控制器 20 …X方问期望心 15 更迅速及稳定， 10 8 昌 10 -15 -10 20 20 2502468101214161820 40 图25重心PD补偿X轴轨迹 tis Fig.25 X-axis trajectory when center of gravity is compen- 图28立抗干扰PD控制器补偿重心变化 sated using PID controller Fig.28 The change of center of gravity is compensated 当加入了PD控制器后，如图24及图25所示 using legislative immunity PID controller 为重心PD补偿X、Y轴轨迹.重心左右方向Y轴移 50 动轨迹明显比未补偿更接近期望重心位置，重心振 30 幅也较为规律稳定，可以看出振幅与未补偿时较为 20 10 稳定且拥有基本的平衡功能 0 80 轴实际乖心(Fuzzy补偿) -20 -30 60 方向期望重心 -40 40 0 t/s 20 0 图29立抗干忧Fuy控制器补偿重心变化 -20 Fig.29 The change of center of gravity is compensated 40 using legislative immunity Fuzzy controller 6002468101214161820 t/s 图26重心uzy补偿Y轴轨迹 Fig.26 Y-axis trajectory when center of gravity is compen sated using Fuzzy controller 图30抗干拢实际测试图 Fig.30 Disturbing the actual test pattern 如图26与图27所示为重心Fuz四补偿X、Y轴 3.3斜坡步行测试 轨迹.当机器人使用模糊控制器时，明显看出重心左 本文透过模糊控制器补偿伺服机角度，使二足 右方向Y轴轨迹较PD控制器更为稳定且较符合期

·470 智能系统学报 第4卷 机器人能够从平坦地面一路步行上倾斜角8°的斜 ped robot using neural networks[C]//Proceedings of IEEE 坡上.如图31为机器人步行于斜坡实际测试图， International Conference on Robotics and Automation.Min- neapolis,USA,1996:240-245. [2]VUKOBRATOVIC M,BOROVAC B.Zero-moment-point thirty five years of its Life[J].International Journal of Hu- manoid Robotics,2004,1:157-173. [3]SARDAIN P,BESSONNET G.Forces acting on a biped ro- bot.Center of pressure-zero moment point[J].IEEE Trans- actions on Systems,Man,and Cybernetics,Part A:Sys tems and Humans,2004,34:630-637. 图31二足机器人上坡测试图 [4]KONNO A,KATO N,SHIRATA S,et al.Development of a light-weight biped humanoid robot C]//Proceedings of Fig.31 The uphill test of biped robot IEEE/RSJ International Conference on Intelligent Robots 4 结论 and Systems.Takamatsu,Japan,2000,3:1565-1570. [5]涂志芳.人型机器人分布式实时控制及步行分析[D]. 主要研究了二足机器人于步行时的动态平衡问 台北：台湾科技大学，2007. 题，透过压力传感器取得二足机器人脚底压力值，并 TU Zhifang.Humanoid robot walking distributed real-time 计算二足机器人的实际重心位置，再将实际重心位 control and analysis[D].Taipei:Taiwan University of Sci- 置以模糊控制器运算，计算二足机器人在步行时各 ence and Technology,2007. [6]葛新成，胡永霞.模糊控制的现状与发展概述[J].现代 伺服机所需补偿角度，并与PD控制器运算做比较， 防御技术，2008,36(3)：51-55. 透过各伺服机角度补偿可明显看出补偿前后的差 GE Xincheng,HU Yongxia.Present analysis and develop- 异经由实际实验测试二足机器人补偿后的波形可 ment trends of Fuzzy control techniques[J].Modern Defence 以得到下列结论： Technolog,2008,36(3):51-55. 1)二足机器人在未补偿重心误差值时，明显看 作者简介： 出重心移动轨迹较不稳定且较没有达到期望重心位 王仲淳，男，1945年生，教授.主要 置，所以在行走时若是地面不平坦或是外界突然有 研究方向为国防太空电力系统、能源及 干扰时则二足机器人就容易倾倒； 发电系统与高科技产业等.发表学术论 2)使用PD控制器时可以看出波形变得较稳 文70余篇. 定且渐渐有重心轨迹出现，但某些时候实际重心位 置与期望重心位置还是有距离，不过此控制器已让 二足机器人行走较为稳定且可以看出二足机器人已 倪世铨，男，1984年生，硕士研究 经拥有了抗干扰性； 生，主要研究方向为智能机器人 3)使用模糊控制器作为补偿角度时，明显地看 出实际重心轨迹与期望轨迹更加相似，使二足机器 人行走更为顺畅及稳定，运用此控制器可以明显看 出二足机器人遇到千扰时，其抗干扰性比使用PD 控制器更强，并使二足机器人能够步行于8°的斜坡 上，这使得机器人行走于不同地形上有所突破。 黄加庆，男，1982年生，硕士研究 生.主要研究方向为智能机器人 参考文献： [1]KUN A,MILLER W T.Adaptive dynamic balance of a bi-