
第4卷第2期 智能系统学报 Vol 4 Ng 2 2009年4月 CAA I Transactions on Intelligent Systems Apr 2009 频繁模式挖掘的约束算法 孟彩霞 西安邮电学院计算机系,陕西西安710065) 摘要:在频繁模式挖据过程中能够动态改变约束的算法比较少.提出了一种基于约束的频繁模式挖掘算法MCFP MC℉P首先按照约束的性质来建立频繁模式树,并且只需扫描一遍数据库,然后建立每个项的条件树挖掘以该项为 前缀的最大频繁模式,并用最大模式树来存储,最后根据最大模式来找出所有支持度明确的频繁模式.MC℉P算法允 许用户在挖掘频繁模式过程中动态地改变约束.实验表明,该算法与C℉P算法相比是很有效的 关键词:频繁模式挖掘:动态约束:频繁项集:最大频繁模式 中图分类号:TP311文献标识码:A文章编号:1673-4785(2009)02014206 A frequent pa ttern m in ing a lgorithm ba sed on con stra n ts MENG Cai-xia (Deparment of Computer Science,Xi'an University of Posts&Telecommunications,Xi'an 710065,China) Abstract:Most algorithms don't allow users to dynam ically change constraints in the process of m ining frequent pattems A new algorithm,constrain-based frequent pattems m ining,was developed to provide frequent pattem mining with constraints First,the algorithm constructs the FP-tree (frequent pattem tree)according to the de- scending or ascending order of constraints,and in this process the database only needs to be scanned once Second- ly,the conditional tree of each item was established to m ine maxmal frequent pattem with this tem as a prefix, and the maximal frequent pattems were stored Finally,all frequent pattems with precise support degrees were dis- covered according to the maxmal frequent pattems The significance of thismethod is that this algorithm allows us- ers to dynam ically change constraints during the process Expermental outcomes showed that the proposed algo- rithm is more efficient than the algorithm of CFP. Keywords:frequent pattems m ining dynam ic constraints frequent item set maxmal frequent pattem 关联规则挖掘是数据挖掘领域研究的重要课进,但是同样存在着这样的问题l,s).Hen等人提出 题.关联规则挖掘问题的解决分为2步:1)找出所 了基于FP-tree结构的不用产生候选项集的FP- 有的频繁项集缬繁模式);2)由频繁项集产生强关 govh算法161,该算法只需扫描2次数据库来建立 联规则.这2步中,频繁项集挖掘是基本步骤,是关 FP-tree,大大提高了挖掘效率.目前,出现了有关挖 联规则挖掘问题的核心1).Agrawal等人提出了经 掘最大频繁模式算法、基于约束的频繁模式挖掘 典的Apriori算法,但是该算法要产生大量的候选 算法[8等.对于交互式频繁模式挖掘,Zhu等人提出 项集并需多次扫描数据库,大大降低了算法的性能. 了UFP-Te算法I,它只是针对支持度不断变化 后来一些类Apriori算法虽然对Apriori做了很多改 的交互式挖掘算法.Leng把约束和交互式相结合提 出了CFP算法o),该算法允许用户在挖掘过程中 收稿日期:2008-12-16 基金项目:陕西省自然科学基金资助项目(2004283);西安市科技创 动态改变约束,且不必重新扫描数据库,但是在找频 新支撑应用发展研究计划资助项目(Y℉07024). 通信作者:孟彩霞.Email:mexmcx(@xiyou edu cn 繁项集时,需要不断建立条件树,占用了大量内存: 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 4卷第 2期 智 能 系 统 学 报 Vol. 4 №. 2 2009年 4月 CAA I Transactions on Intelligent System s Ap r. 2009 频繁模式挖掘的约束算法 孟彩霞 (西安邮电学院 计算机系 ,陕西 西安 710065) 摘 要 :在频繁模式挖掘过程中能够动态改变约束的算法比较少. 提出了一种基于约束的频繁模式挖掘算法 MCFP. MCFP首先按照约束的性质来建立频繁模式树 ,并且只需扫描一遍数据库 ,然后建立每个项的条件树 ,挖掘以该项为 前缀的最大频繁模式 ,并用最大模式树来存储 ,最后根据最大模式来找出所有支持度明确的频繁模式. MCFP算法允 许用户在挖掘频繁模式过程中动态地改变约束. 实验表明 ,该算法与 iCFP算法相比是很有效的. 关键词 :频繁模式挖掘 ;动态约束 ;频繁项集 ;最大频繁模式 中图分类号 : TP311 文献标识码 : A 文章编号 : 167324785 (2009) 0220142206 A frequent pattern m in ing algor ithm based on constra ints MENG Cai2xia (Department of Computer Science, Xi’an University of Posts & Telecommunications, Xi’an 710065, China) Abstract:Most algorithm s don’t allow users to dynam ically change constraints in the p rocess of m ining frequent patterns. A new algorithm, constrain2based frequent patterns m ining, was developed to p rovide frequent pattern m ining with constraints. First, the algorithm constructs the FP2tree ( frequent pattern tree) according to the de2 scending or ascending order of constraints, and in this p rocess the database only needs to be scanned once. Second2 ly, the conditional tree of each item was established to m ine maximal frequent pattern with this term as a p refix, and the maximal frequent patternswere stored. Finally, all frequent patternswith p recise support degreeswere dis2 covered according to the maximal frequent patterns. The significance of thismethod is that this algorithm allows us2 ers to dynam ically change constraints during the p rocess. Experimental outcomes showed that the p roposed algo2 rithm is more efficient than the algorithm of iCFP. Keywords: frequent patterns m ining; dynam ic constraints; frequent item set; maximal frequent pattern 收稿日期 : 2008212216. 基金项目 :陕西省自然科学基金资助项目 (2004f283) ; 西安市科技创 新支撑 —应用发展研究计划资助项目 ( YF07024). 通信作者 :孟彩霞. E2mail: mcxmcx@xiyou. edu. cn 关联规则挖掘是数据挖掘领域研究的重要课 题. 关联规则挖掘问题的解决分为 2步 : 1)找出所 有的频繁项集 (频繁模式 ) ; 2)由频繁项集产生强关 联规则. 这 2步中 , 频繁项集挖掘是基本步骤 ,是关 联规则挖掘问题的核心 [ 123 ] . Agrawal等人提出了经 典的 Ap riori算法 [ 4 ] ,但是该算法要产生大量的候选 项集并需多次扫描数据库 ,大大降低了算法的性能. 后来一些类 Ap riori算法虽然对 Ap riori做了很多改 进 ,但是同样存在着这样的问题 [ 1, 5 ] . Hen等人提出 了基于 FP2tree 结构的不用产生候选项集的 FP2 growth算法 [ 6 ] ,该算法只需扫描 2次数据库来建立 FP2tree,大大提高了挖掘效率. 目前 ,出现了有关挖 掘最大频繁模式算法 [ 7 ]、基于约束的频繁模式挖掘 算法 [ 8 ]等. 对于交互式频繁模式挖掘 , Zhu等人提出 了 IUFP2Tree算法 [ 9 ] ,它只是针对支持度不断变化 的交互式挖掘算法. Leng把约束和交互式相结合提 出了 iCFP算法 [ 10 ] ,该算法允许用户在挖掘过程中 动态改变约束 ,且不必重新扫描数据库 ,但是在找频 繁项集时 ,需要不断建立条件树 ,占用了大量内存

第2期 孟彩霞:频繁模式挖掘的约束算法 ·143· 提出了一个在频繁模式挖掘过程中可以改变约 调性约束 束的算法,该算法不用反复建立条件树,且在建树时 定义6单调性(monotone)约束.如果项集X 是按照约束的大小顺序来建立的,并且每次只有一 满足约束0,它的所有超集也都满足,则日是单调性 个条件树存在于内存中,挖掘完该条件树后立即释 约束 放,和现有的CFP相比节省了大量内存.为了验证 定义7简洁性(succinct)约束.如果可以直接 算法的性能,进行了一系列的实验来评价算法,实验 精确地产生满足约束的所有项集,而不用产生不满 表明该算法的优越性是明显的」 足约束的项集,则该约束日为简洁性约束, 例如,mn(XA)≥v是简洁反单调性约束 1问题定义 max(XA)≥v是简洁单调性约束 设1={,五,}是n个不同项目的集合, 2算法MCFP 其中)=1,2.,n)是数据单项.事务数据库 DB=,其中每个事务T1=1,2 算法MCFP是针对CFP存在的问题(即不断建 m)是中一组项目的集合,即工三1T有一个 立条件树)而提出的一种改进方法。 惟一的标识符TD. 21数据结构 定义1对于一个集合X,如果X三1且X包 表1和表2分别是一个事务数据库和一个数据 含k个项目,则称X为k-项集,简称为项集 单项的属性表.这里假设数据单项有属性A和B. 定义2如果项集X三工,则称事务T包含项 表1事务数据库 集X:项集X在事务数据库DB中的支持度,记为 Table 1 Transaction datbase SupDa(X),即事务数据库DB中包含项集X的事务 TD Items 个数 1 abed 2 bdf 定义3如果项集X在事务数据库DB中的支 3 abce 持度Supe(X)不小于用户或专家给定的最小支持 4 abde 度阈值δ则称项集X为频繁项集倾繁模式):反之 称之为非频繁项集 表2数据单项的属性表 定义4给定最小支持度δ,对于项集X三1若 Table 2 A ttr butes of da ta item Sups(X)≥6,且对于廿Y(Y∈I∧XCY),均有 item A B Supe(Y)<6,则称X为DB中的最大频繁项集或 60 300 称最大频繁模式).也就是说,如果频繁项集X的所 B 30 400 C 35 500 有超集都是非频繁项集,那么X为最大频繁项集 D 40 450 性质1频繁项集的任何真子集都不是最大频 E 55 600 繁项集 F 65 380 性质2频繁项集的任何子集都是频繁项集」 这里按照属性A上值的大小顺序来建立P 显然,任何频繁项集都是某一个最大频繁项集 tree,这样仅需扫描一遍数据库,然后建立满足简洁 的子集,所以可以把挖掘所有频繁项集的问题转化 性约束的项的条件树.假设简洁性约束为C,= 为挖掘最大频繁项集的问题 mm(sA)≥30,最小支持度6=2 对于项目集合中的每个单项可能有预先定义 在FP-tee中设计了2个数据结构:List和FP- 的属性,例如有属性A、B.定义在项集上的约束0∈ tree List)用于存储可能的频繁单项,FP-tree用于存 {tue,false},如果0(X)=tnue,则项集X满足该约 储可能的频繁项集,具体说明如下: 束.目前常用的约束分为3大类:反单调性约束、单 List一个三元组表.每个三元组(A,item 调性约束和简洁性约束 name,8),其中A是数据单项属性表中有约束的属 定义5反单调性(antimonotone)约束.如果项 性上的分量值,item-name是单项的名称,8是该项 集X不满足约束日,它的超集也不满足,则0是反单 的支持度.Ls表中三元组按照A上的值从大到小 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
提出了一个在频繁模式挖掘过程中可以改变约 束的算法 ,该算法不用反复建立条件树 ,且在建树时 是按照约束的大小顺序来建立的 ,并且每次只有一 个条件树存在于内存中 ,挖掘完该条件树后立即释 放 ,和现有的 iCFP相比节省了大量内存. 为了验证 算法的性能 ,进行了一系列的实验来评价算法 ,实验 表明该算法的优越性是明显的. 1 问题定义 设 I = { i1 , i2 , …, in } 是 n个不同项目的集合 , 其中 ij ( j = 1, 2, …, n) 是数据单项. 事务数据库 DB = ,其中每个事务 Tj ( j = 1, 2, …, m ) 是 I中一组项目的集合 ,即 Tj Α I, Tj有一个 惟一的标识符 TID. 定义 1 对于一个集合 X,如果 X Α I,且 X 包 含 k个项目 ,则称 X 为 k - 项集 ,简称为项集. 定义 2 如果项集 X Α Tj ,则称事务 Tj包含项 集 X; 项集 X 在事务数据库 DB 中的支持度 , 记为 SupDB (X ) ,即事务数据库 DB 中包含项集 X 的事务 个数. 定义 3 如果项集 X 在事务数据库 DB 中的支 持度 SupDB (X ) 不小于用户或专家给定的最小支持 度阈值 δ,则称项集 X为频繁项集 (频繁模式 ) ;反之 称之为非频繁项集. 定义 4 给定最小支持度δ,对于项集 X Α I,若 SupDB (X ) ≥δ,且对于 Π Y ( Y Α I ∧ X < Y) ,均有 SupDB ( Y) <δ,则称 X为 DB 中的最大频繁项集 (或 称最大频繁模式 ). 也就是说 ,如果频繁项集 X 的所 有超集都是非频繁项集 ,那么 X为最大频繁项集. 性质 1 频繁项集的任何真子集都不是最大频 繁项集. 性质 2 频繁项集的任何子集都是频繁项集. 显然 , 任何频繁项集都是某一个最大频繁项集 的子集 , 所以可以把挖掘所有频繁项集的问题转化 为挖掘最大频繁项集的问题. 对于项目集合 I中的每个单项可能有预先定义 的属性 ,例如有属性 A、B. 定义在项集上的约束 θ∈ { true, false} ,如果 θ(X ) = true,则项集 X满足该约 束. 目前常用的约束分为 3大类 :反单调性约束、单 调性约束和简洁性约束. 定义 5 反单调性 ( anti2monotone)约束. 如果项 集 X不满足约束 θ,它的超集也不满足 ,则 θ是反单 调性约束. 定义 6 单调性 (monotone)约束. 如果项集 X 满足约束 θ,它的所有超集也都满足 ,则 θ是单调性 约束. 定义 7 简洁性 ( succinct)约束. 如果可以直接 精确地产生满足约束的所有项集 ,而不用产生不满 足约束的项集 ,则该约束 θ为简洁性约束. 例如 , m in (X. A ) ≥ v是简洁反单调性约束 , max (X. A ) ≥ v是简洁单调性约束. 2 算法 MCFP 算法 MCFP是针对 iCFP存在的问题 (即不断建 立条件树 )而提出的一种改进方法. 2. 1 数据结构 表 1和表 2分别是一个事务数据库和一个数据 单项的属性表. 这里假设数据单项有属性 A和 B. 表 1 事务数据库 Table 1 Tran saction da taba se TID Item s 1 abcd 2 bdf 3 abce 4 abde 表 2 数据单项的属性表 Table 2 A ttr ibutes of da ta item item A B A 60 300 B 30 400 C 35 500 D 40 450 E 55 600 F 65 380 这里按照属性 A 上值的大小顺序来建立 FP2 tree,这样仅需扫描一遍数据库 ,然后建立满足简洁 性约束的项的条件树. 假设简洁性约束为 Cs = m in (s. A ) ≥30,最小支持度 δ = 2. 在 FP2tree中设计了 2个数据结构 : L ist和 FP2 tree. L ist用于存储可能的频繁单项 , FP2tree用于存 储可能的频繁项集 ,具体说明如下 : L ist:一个三元组表. 每个三元组 ( A , item2 name, δ) ,其中 A是数据单项属性表中有约束的属 性上的分量值 , item2name是单项的名称 , δ是该项 的支持度. L ist表中三元组按照 A 上的值从大到小 第 2期 孟彩霞 :频繁模式挖掘的约束算法 ·143·

·144 智能系统学报 第4卷 或从小到大)顺序排列 调性约束)或由小到大(简洁反单调性约束)创建 FP-tree:一个字典树,每个节点是一个对偶(r List表; tem-name,.F),其中item-name是项名,F是由FP- 2)初始化FP-tree,根指针T为“NULL”: tree的根节点至当前节点的路径上所有项组成的项 3)ForDB中的每个事务t 集的支持度 ①事务的项集已经是T的一个分支(仔 2.2建立FP-tree 树){ 建立FP-tree的步骤如下: ② 该分支上的节点N的支持度增加1; 1)把项按照A的值从大到小顺序排序,放进 ③ List中该项集的每个单项的支持度增加 List表中 1,} 2)扫描事务数据库,根据List中项的顺序建立 ④ Else FP-tree,把每次涉及到的项的支持度(卿List表中项 ⑤ 创建新的节点N,存放事务T的项集: 的δ值)加1,直到最后一个事务,同时建立相同项 ⑥ 节点N和T连接起来; 之间的连接.此时包含非频繁项的树建立完毕, ⑦ 具有相同项的节点连接起来;} 如图所示 ⑧Endf List Root ⑨End For 65 4)fN的支持度小于最小支持度 60a 5)删除节点N以及和N有关的连接: 55e 2 6)End If 40d3 23建立满足约束的条件树找出最大频繁模式 e:I 35 首先从Lst表中最后一项开始,判断各项是否 30b4 b:1-=b:1 满足给定的条件.如果不满足,则不用建立该项的条 件树,这样就把约束放到了挖掘过程中,根据约束的 图1包含非频繁项的树的结构 性质来降低搜索空间.如果找到满足约束的项,则建 Fig 1 Tree included infrequent item set 立该项的条件树,并把该树中的非频繁项即局部非 3)查Ls表去掉表中非频繁项.当去掉非频繁项 频繁项去掉.由图2可知,最后一项是b,b满足假设 时,根据连接重新调整树的结构.由图1中List可知f 的简洁性约束C,=min (sA)≥30,b的条件树 的支持度小于2,去掉项f后的FP-tree如图2所示. 如图3所示.由于b的条件树中没有局部非频繁项, Root 所以不用再重新调整该树的结构 List e:2 h4 60 c:I 30b 4 h 图2FP-tree结构 图3b的条件树 Fig 2 FP-tree structure Fig 3 Condition-tree of b 算法1建立FP-tree的算法】 然后用该树的分支两两相交来得到局部最大 输入:DB,最小支持度8,简洁性约束; 频繁模式.例如b的条件树前2个分支bcae:1和 输出:FP-tee bcda:1相交得到bca:2然后按照支持度由大到小 方法: 的顺序插入到最大模式树中.最大模式树初始值为 1)按照每个单项的属性A值由大到小(简洁单 空,如果某项集已存在于最大模式树中或是已存在 的最大模式树的子集,则不再插入该项集.挖掘完b 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
(或从小到大 )顺序排列. FP2tree:一个字典树 ,每个节点是一个对偶 ( i2 tem2name, F ) ,其中 item2name是项名 , F是由 FP2 tree的根节点至当前节点的路径上所有项组成的项 集的支持度. 2. 2 建立 FP2tree 建立 FP2tree的步骤如下 : 1)把项按照 A 的值从大到小顺序排序 ,放进 List表中. 2)扫描事务数据库 ,根据 L ist中项的顺序建立 FP2tree,把每次涉及到的项的支持度 (即 L ist表中项 的 δ值 )加 1,直到最后一个事务 ,同时建立相同项 之间的连接. 此时包含非频繁项的树建立完毕 , 如图 1所示. 图 1 包含非频繁项的树的结构 Fig. 1 Tree included infrequent item set 3)查 List表去掉表中非频繁项.当去掉非频繁项 时 ,根据连接重新调整树的结构. 由图 1中 List可知 f 的支持度小于 2,去掉项 f后的 FP2tree如图 2所示. 图 2 FP2tree结构 Fig. 2 FP2tree structure 算法 1 建立 FP2tree的算法. 输入 : DB, 最小支持度 δ,简洁性约束 ; 输出 : FP2tree 方法 : 1)按照每个单项的属性 A值由大到小 (简洁单 调性约束 )或由小到大 (简洁反单调性约束 )创建 List表 ; 2)初始化 FP2tree,根指针 T为“NULL”; 3) For DB中的每个事务 t ① If事务 t的项集已经是 T的一个分支 (子 树 ) { ② 该分支上的节点 N 的支持度增加 1; ③ List中该项集的每个单项的支持度增加 1; } ④ Else { ⑤ 创建新的节点 N,存放事务 T的项集; ⑥ 节点 N 和 T连接起来 ; ⑦ 具有相同项的节点连接起来 ; } ⑧ End If ⑨End For 4) IfN 的支持度小于最小支持度 5)删除节点 N 以及和 N 有关的连接 ; 6) End If 2. 3 建立满足约束的条件树找出最大频繁模式 首先从 L ist表中最后一项开始 ,判断各项是否 满足给定的条件. 如果不满足 ,则不用建立该项的条 件树 ,这样就把约束放到了挖掘过程中 ,根据约束的 性质来降低搜索空间. 如果找到满足约束的项 ,则建 立该项的条件树 ,并把该树中的非频繁项即局部非 频繁项去掉. 由图 2可知 ,最后一项是 b, b满足假设 的简洁性约束 Cs = m in (s. A ) ≥ 30, b的条件树 如图 3所示. 由于 b的条件树中没有局部非频繁项 , 所以不用再重新调整该树的结构. 图 3 b的条件树 Fig. 3 Condition2tree of b 然后用该树的分支两两相交来得到局部最大 频繁模式. 例如 b的条件树前 2个分支 bcae: 1和 bcda: 1相交得到 bca: 2. 然后按照支持度由大到小 的顺序插入到最大模式树中. 最大模式树初始值为 空 ,如果某项集已存在于最大模式树中或是已存在 的最大模式树的子集 ,则不再插入该项集. 挖掘完 b ·144· 智 能 系 统 学 报 第 4卷

第2期 孟彩霞:频繁模式挖掘的约束算法 ·145- 的条件树后得到的最大模式树如图4所示 6) 把这些路径插入M的条件树中; Root 7) 把条件树中的相同项连接起来; 8) 调用m ining(M-conditional tree); 9) 释放M的条件树;}} 10)最大频繁模式即为MFT的每个分支 算法3 m ining(M-conditional tree)算法 d:2.c:2e:2 输入:条件树M-conditional tree,最小支持度8; 输出:局部最大频繁模式(MFT) 图4挖掘完b条件树后的最大模式树 1)IMFT=: Fig 4 Maxmal pattems tree after m ining b 2)M的条件树的每个分支两两相交得到局部 同理,分别建立cda、e的条件树,依次得到局 频繁模式P 部最大模式插入到最大模式中,最后得到的最大模 3)按照支持度递减的顺序把P插入到MFT中; 式树即为图4所示。 4)如果该局部频繁模式存在于MFT中或是 由图4可知,最后的最大频繁模式为bac2、 MFT的子集: bae:2、bad2 5)不需要插入该局部频繁模式: 如果还需要其他的频繁模式,只需从最大频繁 模式中得到所需要的模式,因为这些模式肯定是最 3MCFP处理动态约束 大频繁模式的子集.所以得到所有的频繁模式很容 当约束变化时约束范围可能是以前范围的超集 易,但得到它们的支持度却不容易,因为最大模式中 也可能是子集.约束范围由小变大时称为松约束性 不包含它们的支持度信息.目前许多算法都是在找 变化(relaxing change),约束范围由大变小时称为紧 到最大模式后再重新扫描一遍数据库来得到所有频 约束性变化(tighting change) 繁模式的支持度信息,这样在重新扫描数据库时算 31处理紧约束性的动态变化 法的性能就降低了.针对这一问题,MCFP算法把支 持度的信息都保存在Lst表中,所以不用重新扫描 设约束由Cu=min(sA)≥30变为Caw= 数据库就很容易得到所有频繁模式的信息.例如,由 min(sA)≥40,显然有SSaw∈SSu,其中SSn是指 新约束的范围,SS是指以前的约束范围所以只需 最大频繁模式bac可以知道它的子模式有ba、bc 在最大模式树中去掉不满足约束的项,即hc删除 αc并且根据简洁性约束的性质,直接就能判断这些 子模式都满足约束条件.现在最主要的就是得到它 bc后的最大模式树如图5所示 Root 们的支持度来判断它们是否频繁.以计算bc的支持 度为例,由List表中包含的频繁项的信息可得b:4、 c2,所以b的支持度以这2项中支持度小的一项为 准,即bc2按照这种方法,最后所有的满足约束的 d:2 :2 频繁模式为ba:3、bd:3、ad:2、bc:2、be2、ae2、bac 2、bae2、badk2 图5约束化后的最大模式树 算法2建立MFT(maxmal frequent pattem Fig 5 Maxmal pattems tree after changed constraint tree). 由图5可得满足约束的最大模式为ad:2 输入:FP-tree最小支持度8、约束; ae2由最大模式可得满足约束的所有频繁模式有 输出:最大频繁模式MFT a:3、d:3、e:3 1)M=List表中的最后一项; 3.2处理松约束性的动态变化 2)M的条件树M-conditional tree=中; 设约束由CoM=min(sA)≥40变为Cnaw= 3)For(i=1:i<=项的个数:i++){; min(sA)≥30,则SSw2SSu.这样b和c也满足约 4)if(min(M.A)≥30){ 束条件了,只需再挖掘6c的条件树,最后把局部频 5) 找出含有项M的所有路径; 繁模式插入到Ca=mim(sA)≥40约束时的最大 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
的条件树后得到的最大模式树如图 4所示. 图 4 挖掘完 b条件树后的最大模式树 Fig. 4 Maximal patterns tree after mining b 同理 ,分别建立 c、d、a、e的条件树 ,依次得到局 部最大模式插入到最大模式中 ,最后得到的最大模 式树即为图 4所示. 由图 4 可知 ,最后的最大频繁模式为 bac: 2、 bae: 2、bad: 2. 如果还需要其他的频繁模式 ,只需从最大频繁 模式中得到所需要的模式 ,因为这些模式肯定是最 大频繁模式的子集. 所以得到所有的频繁模式很容 易 ,但得到它们的支持度却不容易 ,因为最大模式中 不包含它们的支持度信息. 目前许多算法都是在找 到最大模式后再重新扫描一遍数据库来得到所有频 繁模式的支持度信息 ,这样在重新扫描数据库时算 法的性能就降低了. 针对这一问题 ,MCFP算法把支 持度的信息都保存在 List表中 ,所以不用重新扫描 数据库就很容易得到所有频繁模式的信息. 例如 ,由 最大频繁模式 bac可以知道它的子模式有 ba、bc、 ac,并且根据简洁性约束的性质 ,直接就能判断这些 子模式都满足约束条件. 现在最主要的就是得到它 们的支持度来判断它们是否频繁. 以计算 bc的支持 度为例 ,由 L ist表中包含的频繁项的信息可得 b: 4、 c: 2,所以 bc的支持度以这 2项中支持度小的一项为 准 ,即 bc: 2. 按照这种方法 ,最后所有的满足约束的 频繁模式为 ba: 3、bd: 3、ad: 2、bc: 2、be: 2、ae: 2、bac: 2、bae: 2、bad: 2. 算法 2 建立 MFT (maximal frequent pattern tree). 输入 : FP2tree、最小支持度 δ、约束 ; 输出 :最大频繁模式 MFT. 1) M =L ist表中的最后一项 ; 2) M 的条件树 M2conditional tree = < ; 3) For( i = 1; i < =项的个数; i ++ ) { ; 4) if( m in ( M. A ) ≥30) { 5) 找出含有项 M 的所有路径 ; 6) 把这些路径插入 M 的条件树中 ; 7) 把条件树中的相同项连接起来 ; 8) 调用 m ining( M 2conditional tree) ; 9) 释放 M 的条件树 ; } } 10)最大频繁模式即为 MFT的每个分支. 算法 3 m ining( M 2conditional tree)算法. 输入:条件树 M 2conditional tree,最小支持度δ; 输出 :局部最大频繁模式 (LMFT) 1) LMFT = <; 2) M 的条件树的每个分支两两相交得到局部 频繁模式 P; 3) 按照支持度递减的顺序把 P插入到 MFT中; 4) 如果该局部频繁模式存在于 MFT中或是 MFT的子集 ; 5) 不需要插入该局部频繁模式. 3 MCFP处理动态约束 当约束变化时约束范围可能是以前范围的超集 也可能是子集. 约束范围由小变大时称为松约束性 变化 ( relaxing change) ,约束范围由大变小时称为紧 约束性变化 ( tighting change). 3. 1 处理紧约束性的动态变化 设约束由 Cold = m in ( s. A ) ≥30 变为 Cnew = m in (s. A ) ≥40,显然有 SSnew Α SSold ,其中 SSnew是指 新约束的范围 , SSold是指以前的约束范围. 所以只需 在最大模式树中去掉不满足约束的项 ,即 b、c. 删除 b、c后的最大模式树如图 5所示. 图 5 约束化后的最大模式树 Fig. 5 Maximal patterns tree after changed constraint 由图 5 可得满足约束的最大模式为 ad: 2、 ae: 2. 由最大模式可得满足约束的所有频繁模式有 a: 3、d: 3、e: 3. 3. 2 处理松约束性的动态变化 设 约 束 由 Cold = m in (s. A ) ≥40变 为 Cnew = m in (s. A ) ≥30,则 SSnew Β SSold . 这样 b和 c也满足约 束条件了 ,只需再挖掘 b、c的条件树 ,最后把局部频 繁模式插入到 Cold =m in ( s. A ) ≥40约束时的最大 第 2期 孟彩霞 :频繁模式挖掘的约束算法 ·145·
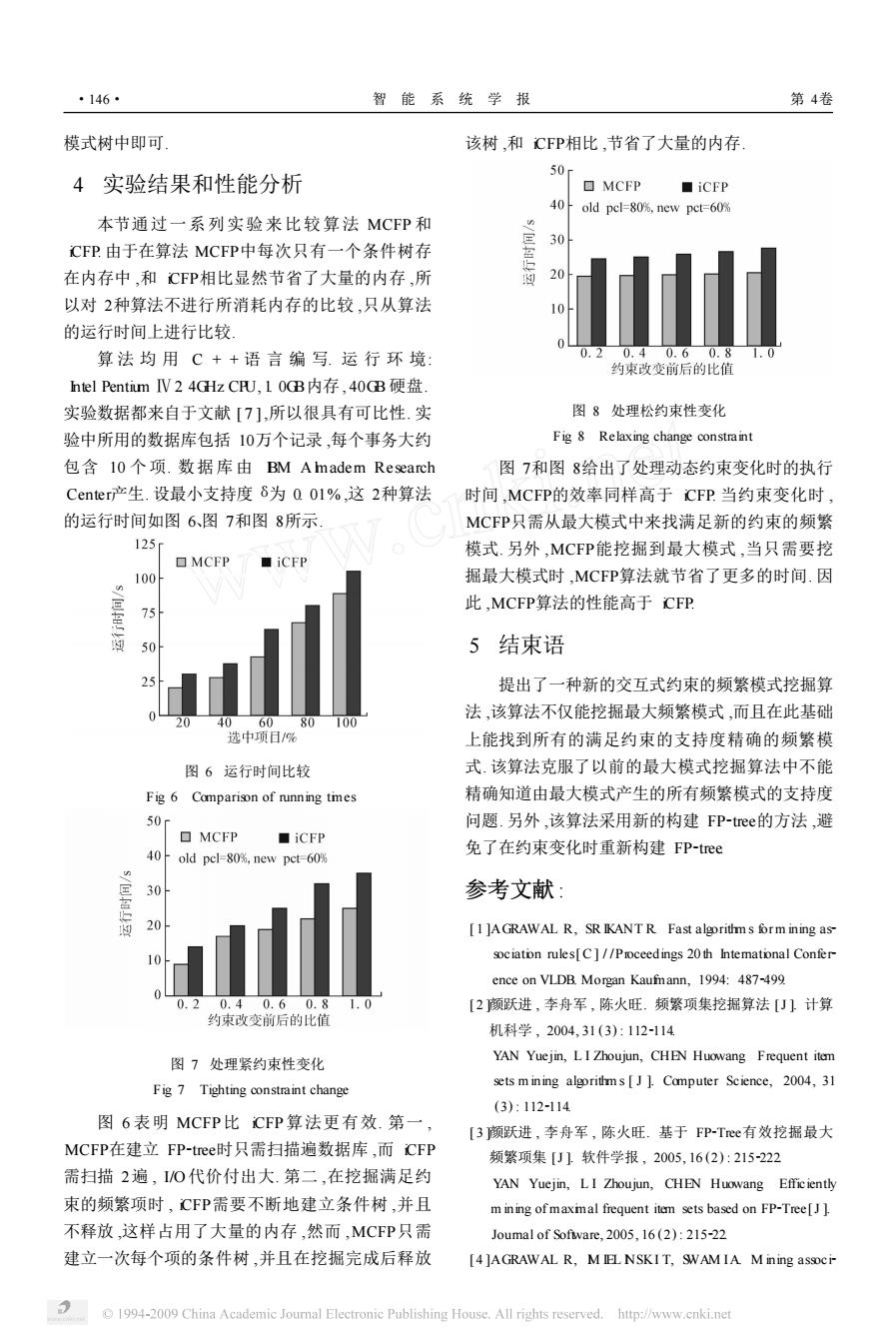
·146 智能系统学报 第4卷 模式树中即可 该树,和CFP相比,节省了大量的内存 4实验结果和性能分析 50r MCFP ■iCFP 40 old pcl=80%,new pct=60% 本节通过一系列实验来比较算法MCFP和 30 CFP由于在算法MCFP中每次只有一个条件树存 在内存中,和C℉P相比显然节省了大量的内存,所 20 以对2种算法不进行所消耗内存的比较,只从算法 的运行时间上进行比较 算法均用C++语言编写.运行环境 0.20.40.60.8 约束改变前后的比值 ntel Pentium IV24 Hz CRU,10GB内存,40GB硬盘. 实验数据都来自于文献【7],所以很具有可比性.实 图8处理松约束性变化 验中所用的数据库包括10万个记录,每个事务大约 Fig 8 Relaxing change constraint 包含l0个项.数据库由BM Amadem Research 图7和图8给出了处理动态约束变化时的执行 Center产生.设最小支持度8为Q01%,这2种算法 时间,MCFP的效率同样高于CFP当约束变化时, 的运行时间如图6、图7和图8所示 MCFP只需从最大模式中来找满足新的约束的频繁 125 模式.另外,MCFP能挖掘到最大模式,当只需要挖 口MCFP ■iCFP 100 掘最大模式时,MCFP算法就节省了更多的时间.因 此,MCFP算法的性能高于CFP 75 50 5结束语 提出了一种新的交互式约束的频繁模式挖掘算 法,该算法不仅能挖掘最大频繁模式,而且在此基础 20 406080 00 选中项日/% 上能找到所有的满足约束的支持度精确的频繁模 图6运行时间比较 式.该算法克服了以前的最大模式挖掘算法中不能 Fig 6 Comparison of running tmes 精确知道由最大模式产生的所有频繁模式的支持度 50r 问题.另外,该算法采用新的构建FP-tree的方法,避 ▣MCFP ■iCFP 40 old pcl=80%,new pct=60% 免了在约束变化时重新构建FP-tree 30 参考文献: 20 1 ]A GRAWAL R,SR IKANT R Fast algorithms orm ining as- sociaton rules[C]//Proceedings 20 th Intemational Confer ence on VLDB.Morgan Kaufnann,1994:487-499 0.20.40.60.8 1.0 [2颜跃进,李舟军,陈火旺.频繁项集挖掘算法[J)计算 约束改变前后的比值 机科学,2004,31(3):112-114 图7处理紧约束性变化 YAN Yuejin,LI Zhoujun,CHEN Huowang Frequent item Fig 7 Tighting constraint change sets m ining algorithms [J ]Computer Science,2004,31 (3):112-114 图6表明MCFP比CFP算法更有效.第一, [3颜跃进,李舟军,陈火旺.基于FP-Tee有效挖掘最大 MCFP在建立FP-tee时只需扫描遍数据库,而CFP 频繁项集[J]软件学报,2005,16(2):215-222 需扫描2遍,1/O代价付出大.第二,在挖掘满足约 YAN Yuejin,LI Zhoujun,CHEN Huowang Efficiently 束的频繁项时,CFP需要不断地建立条件树,并且 m ining ofmaxmal frequent item sets based on FP-Tree[J. 不释放,这样占用了大量的内存,然而,MCFP只需 Joumal of Sofware,2005,16(2):215-22 建立一次每个项的条件树,并且在挖掘完成后释放 [4 ]AGRAWAL R,M IEL NSKI T,SWAMIA M ining associ 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
模式树中即可. 4 实验结果和性能分析 本节通过一系列实验来比较算法 MCFP 和 iCFP. 由于在算法 MCFP中每次只有一个条件树存 在内存中 ,和 iCFP相比显然节省了大量的内存 ,所 以对 2种算法不进行所消耗内存的比较 ,只从算法 的运行时间上进行比较. 算 法 均 用 C + + 语 言 编 写. 运 行 环 境: Intel Pentium Ⅳ2. 4GHz CPU, 1. 0GB内存 , 40GB 硬盘. 实验数据都来自于文献 [ 7 ],所以很具有可比性. 实 验中所用的数据库包括 10万个记录 ,每个事务大约 包含 10 个项. 数据库由 IBM A lmadern Research Center产生. 设最小支持度 δ为 0. 01% ,这 2种算法 的运行时间如图 6、图 7和图 8所示. 图 6 运行时间比较 Fig. 6 Comparison of running times 图 7 处理紧约束性变化 Fig. 7 Tighting constraint change 图 6 表明 MCFP比 iCFP算法更有效. 第一 , MCFP在建立 FP2tree时只需扫描遍数据库 ,而 iCFP 需扫描 2遍 , I/O代价付出大. 第二 ,在挖掘满足约 束的频繁项时 , iCFP需要不断地建立条件树 ,并且 不释放 ,这样占用了大量的内存 ,然而 ,MCFP只需 建立一次每个项的条件树 ,并且在挖掘完成后释放 该树 ,和 iCFP相比 ,节省了大量的内存. 图 8 处理松约束性变化 Fig. 8 Relaxing change constraint 图 7和图 8给出了处理动态约束变化时的执行 时间 ,MCFP的效率同样高于 iCFP. 当约束变化时 , MCFP只需从最大模式中来找满足新的约束的频繁 模式. 另外 ,MCFP能挖掘到最大模式 ,当只需要挖 掘最大模式时 ,MCFP算法就节省了更多的时间. 因 此 ,MCFP算法的性能高于 iCFP. 5 结束语 提出了一种新的交互式约束的频繁模式挖掘算 法 ,该算法不仅能挖掘最大频繁模式 ,而且在此基础 上能找到所有的满足约束的支持度精确的频繁模 式. 该算法克服了以前的最大模式挖掘算法中不能 精确知道由最大模式产生的所有频繁模式的支持度 问题. 另外 ,该算法采用新的构建 FP2tree的方法 ,避 免了在约束变化时重新构建 FP2tree. 参考文献 : [ 1 ]AGRAWAL R, SR IKANT R. Fast algorithm s formining as2 sociation rules[ C ] / /Proceedings 20 th International Confer2 ence on VLDB. Morgan Kaufmann, 1994: 4872499. [ 2 ]颜跃进 , 李舟军 , 陈火旺. 频繁项集挖掘算法 [J ]. 计算 机科学 , 2004, 31 (3) : 1122114. YAN Yuejin, L I Zhoujun, CHEN Huowang. Frequent item sets m ining algorithm s [ J ]. Computer Science, 2004, 31 (3) : 1122114. [ 3 ]颜跃进 , 李舟军 , 陈火旺. 基于 FP2Tree有效挖掘最大 频繁项集 [J ]. 软件学报 , 2005, 16 (2) : 2152222. YAN Yuejin, L I Zhoujun, CHEN Huowang. Efficiently m ining of maximal frequent item sets based on FP2Tree[J ]. Journal of Software, 2005, 16 (2) : 215222. [ 4 ]AGRAWAL R, IM IEL INSKI T, SWAM IA. M ining associ2 ·146· 智 能 系 统 学 报 第 4卷

第2期 孟彩霞:频繁模式挖掘的约束算法 ·147· ation rules between sets of items in large database [C]// quential pattem m ining algorithm based on PrefixSpan [J] Proc of the ACM SIMOD Conf on Management of Data Joumal of Southeast University.Natural Science Edition, Washington,DC 1993:207-216 2005,35(5):692-696 [5]SR IKANT R,AGRAW AL R.Mining sequential patters [9]ZHU Qunxiong.LN Xiaoyong Mining frequent pattems generalizations and peromance mprovements [C]//Proc with incremental updating frequent pattem tree [C ]//The of the 5th Int'I Conf on Extending Database Technolgy 6th World Congress on Intelligent Control and Automaton Berlin:SpringerVerlag.1996:3-17 Dalian,.2006:125-128 [6]PEIJ,HAN J,PNTO H,et al Mining sequential pattems [10 ]LENG Kaisong Interactive constrained frequentpattem efficiently by prefix-projected pattem growth[C]//The 17th m ining system [C]//Proc of the It'1 Database Engineer Int'1 Conf on Data Engineering Heidelberg.Gemany, ing and Applications Symposium (DEAS'04).Los 2001:195-201 A lamitos,CA:IEEE Computer Society Press,2004:48- [7]BURD CCK D,CAL MMM,GEHRKE J.A maxial fre- 58 quent item set algorithm for transactional database[C]//Pis- 作者简介: cataway,NJ:IEEE Press,2001:443-452 孟彩霞,女,1966年生,副教授,主 [8陆介平,刘月波,倪巍伟.基于PrefixSpan的快速交互 要研究方向为数据库、数据挖掘等· 序列模式挖掘算法[小]东南大学学报:自然科学版, 2005,35(5):692-696 LU Jiep ing,L U Yuebo,NIWeiwei Fast interactive se- 第2届智能计算技术与自动化国际会议 The Second hterna tional Conference on I telligent Com puta tion Technology and Automa tion C ICTA 2009 ams to provide a high-level intemational form for scientists,engineers,and educators to present the state of the art of intelligent computation and automation research and applications in diverse fields The conference will feature plenary peeches given by renowned scholars and regular sessions with broad coverage All accepted papers will appear in conference proceedings published by the IEEE Computer Society and will be indexed both EI(Compendex)and ISTP Relevant topics include,but are not lm ited to: Advanced Computation Theory,Application and Smulation OControl Theory,Application and Test-bed OAutomation and Smulation OMechanic Manufacturing System and Engineering Optm ization ODecision and Management Prospective authors are encouraged to subm it a full paper for review in PDF fommat Only original papers that have not been published or subm itted for publication elsewhere will be considered The subm ission process is carried through C CTA09 conference management system.The manuscripts must follow the IEEE CS fomat W eb site:http://www.icicta org. 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
ation rules between sets of item s in large database [ C ] / / Proc of the ACM SIGMOD Conf on Management of Data. W ashington, DC 1993: 2072216. [ 5 ] SR IKANT R, AGRAWAL R. M ining sequential patterns: generalizations and performance imp rovements[ C ] / / Proc of the 5 th Int’1 Conf on Extending Database Technology. Berlin: Sp ringer2Verlag, 1996: 3217. [ 6 ] PEIJ, HAN J, P INTO H, et al. M ining sequential patterns efficiently by p refix2p rojected pattern growth[C ] / / The 17 th Int’1 Conf on Data Engineering. Heidelberg, Germany, 2001: 1952201. [ 7 ]BURD ICK D, CAL IM IM M, GEHRKE J. A maximal fre2 quent itemset algorithm for transactional database[C ] / /Pis2 cataway,NJ: IEEE Press, 2001: 4432452. [ 8 ]陆介平 , 刘月波 , 倪巍伟. 基于 PrefixSpan的快速交互 序列模式挖掘算法 [ J ]. 东南大学学报 :自然科学版 , 2005, 35 (5) : 6922696. LU Jiep ing, L IU Yuebo, N IW eiwei. Fast interactive se2 quential pattern m ining algorithm based on PrefixSpan [J ]. Journal of Southeast University: Natural Science Edition, 2005, 35 (5) : 6922696. [ 9 ] ZHU Qunxiong, L IN Xiaoyong. M ining frequent patterns with incremental updating frequent pattern tree [ C ] / /The 6 th World Congress on Intelligent Control and Automation. Dalian, 2006: 1252128. [ 10 ] LENG Kaisong. Interactive constrained frequent2pattern mining system [C ] / /Proc of the Int’1 Database Engineer2 ing and App lications Symposium ( IDEAS’04 ). Los A lam itos, CA: IEEE Computer Society Press, 2004: 482 58. 作者简介 : 孟彩霞 ,女 , 1966年生 ,副教授 ,主 要研究方向为数据库、数据挖掘等 . 第 2届智能计算技术与自动化国际会议 The Second International Conference on Intelligent Computation Technology and Automation ICICTA 2009 aims to p rovide a high2level international forum for scientists, engineers, and educators to p resent the state of the art of intelligent computation and automation research and app lications in diverse fields. The conference will feature p lenary speeches given by renowned scholars and regular sessions with broad coverage. All accep ted papers will appear in conference p roceedings published by the IEEE Computer Society and will be indexed both EI (Compendex) and ISTP. Relevant top ics include, but are not limited to: ●Advanced Computation Theory, App lication and Simulation ●Control Theory, App lication and Test2bed ●Automation and Simulation ●Mechanic Manufacturing System and Engineering Op timization ●Decision and Management Prospective authors are encouraged to submit a full paper for review in PDF format. Only original papers that have not been published or submitted for publication elsewhere will be considered. The submission p rocess is carried through ICICTA09 conference management system. The manuscrip ts must follow the IEEE CS format. W eb site: http: / /www. icicta. org. . 第 2期 孟彩霞 :频繁模式挖掘的约束算法 ·147·