
第4卷第6期 智能系统学报 Vol.4 No.6 2009年12月 CAAI Transactions on Intelligent Systems Dec.2009 doi:10.3969/j.issn.16734785.2009.06.011 基于阿克曼原理的车式移动机器人运动学建模 任孝平,蔡自兴 (中南大学信息科学与工程学院,湖南长沙410083) 摘要:基于阿克曼原理的轮式移动机器人运动学模型对于无人驾驶车辆的研究有着重要的意义.对轮式移动机器 人的运动学特性进行了分析,建立了不考虑滑行、刹车等的轮式移动机器人的运动学模型.对该运动学模型引入了 阿克曼约束,给出了描述机器人运动状态的转向角、航向角和转弯半径等物理量的数学公式.最后对该运动学模型 进行仿真实验,验证了所建立的运动学模型的正确性,为进一步研究轮式移动机器人提供了理论分析的基础. 关键词:轮式移动机器人;运动学模型;阿克曼原理;转向特性 中图分类号:TP242.6文献标识码:A文章编号:16734785(2009)06053404 Using the Ackerman principle for kinematic modeling of wheeled mobile robots REN Xiao-ping,CAI Zi-xing (School of Information Science Engineering,Central South University,Changsha 410083,China) Abstract:Applying the Ackerman principle to kinematic modeling of wheeled mobile robots is of vital importance for improving the performance of unmanned autonomous vehicles.The kinematic characteristics of wheeled mobile robots were analyzed in this paper,and a kinematic model was set up that did not consider sliding or braking.The Ackerman principle was then introduced to this kinematic model.Mathematical formulas were proposed for turning angle,steering angle and turning radius.These accurately reflect the movement status of the mobile robot,provi- ding a theoretical basis for analysis of future intelligent vehicles.The conclusions were validated through a simula- tion. Keywords:wheeled mobile robot;kinematics model;Ackerman principle;turning characteristics 自主移动机器人的运动轨迹控制至关重要,而而对整个机器人的运动学有很大的影响].普通汽 确定运动轨迹的关键因素是建立准确的运动学模 车大都为高度标准化的环境(公路网络)而设计,全 型,它是对机械系统如何运动的最基本的研 部共享相同的轮子结构,使得它们对标准化环境的 究[2].目前有关运动学的理论分析和建模方法已经 这些品质可以最大化.汽车中广泛采用的Ackerman 得到了深入的研究,而且广泛地应用于各种类型的 (阿克曼)轮子结构,除了应用于为道路系统设计的 移动机器人上1,34 移动机器人外,其他机器人很少使用.文献[7]主要 机器人的运动机构较之普通的车辆来说更为复 研究了控制四轮车辆的稳定驾驶的问题,目前对四 杂,因为它要能应用在种类繁多的环境中.由于不同 轮车式移动机器人的运动学建模的文献相对较少. 的移动机器人面临各种不同环境,没有单一的轮子 1四轮车式机器人的运动学建模 结构可以使它们对环境的机动性、可控性和稳定性 达到最大.目前移动机器人的轮子结构种类繁 首先对四轮车辆的水平面运动进行研究.在整 多),常用的轮子类型有[6:标准轮、小脚轮、瑞典 个分析过程中,将机器人建模成轮子上的一个刚体, 轮和球形轮等.在运动学方面,它们的差别很大,从 运行在水平面上时,车轮与地面只有点接触,轮子不 可发生形变且是纯滚动,不发生滑行、刹车等行为, 收稿日期:2009-1002 基金项目:国家自然科学基金资助项目(90820302,60805027);国家 忽略车轮外倾、侧偏以及轮胎的影响8].针对车式 博士点基金资助项目(200805330005):湖南省院士基金资 机器人的运动学建模,不能单一用后轴中点进行建 助项目(2009FJ4030). 通信作者:任孝平.E-mail:xiaopingren(@gmail.com. 模],还应该取前轴或者其他参考点.这是因为车
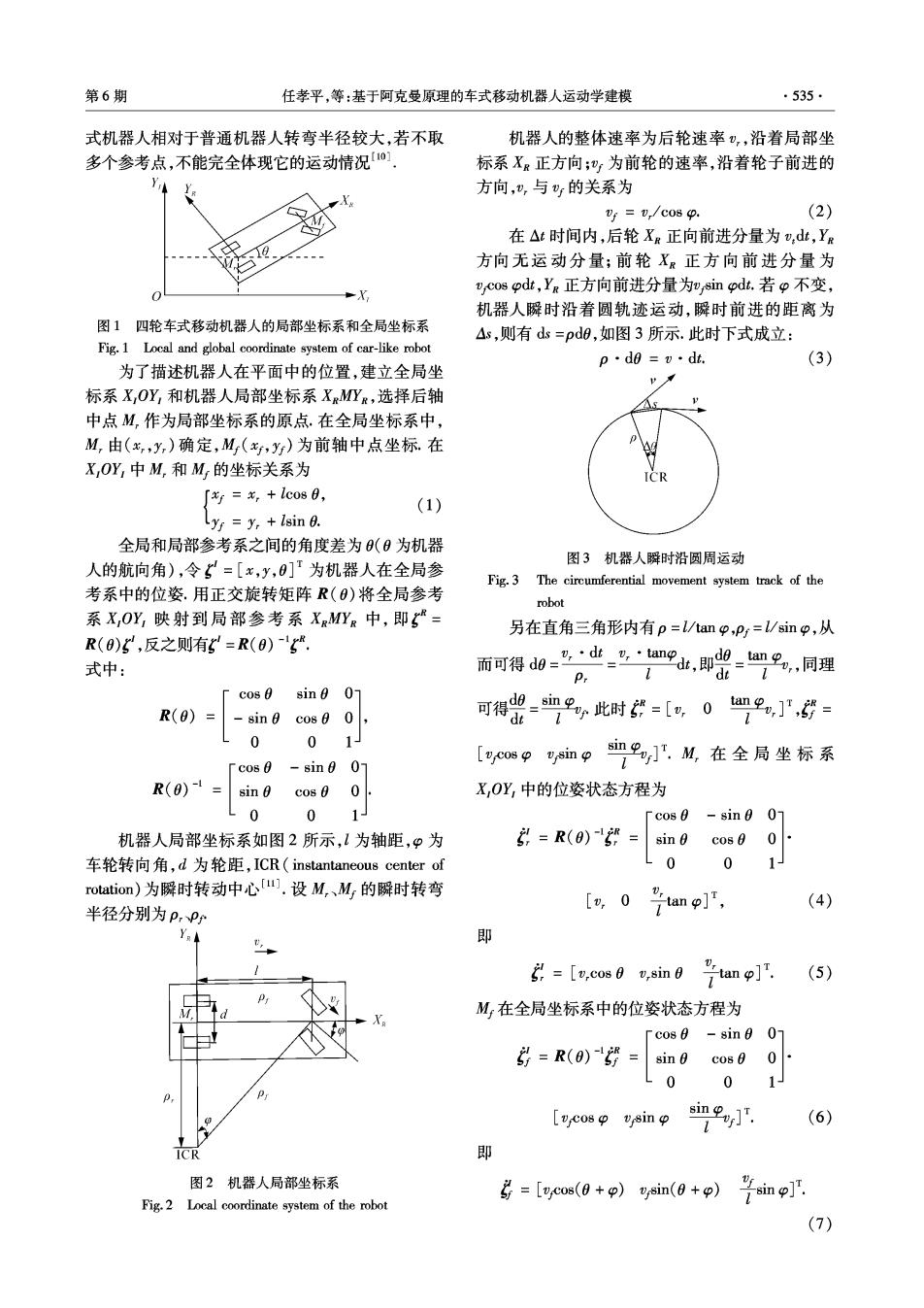
第6期 任孝平,等:基于阿克曼原理的车式移动机器人运动学建模 ·535· 式机器人相对于普通机器人转弯半径较大,若不取 机器人的整体速率为后轮速率),沿着局部坐 多个参考点,不能完全体现它的运动情况, 标系XR正方向;巴为前轮的速率,沿着轮子前进的 方向,”,与巴的关系为 y=,/c08p. (2) 在△t时间内,后轮Xg正向前进分量为,dt,Y 方向无运动分量:前轮XR正方向前进分量为 cos odt,YR正方向前进分量为v sin odt.若p不变, 机器人瞬时沿着圆轨迹运动,瞬时前进的距离为 图1四轮车式移动机器人的局部坐标系和全局坐标系 △s,则有ds=pd0,如图3所示.此时下式成立: Fig.1 Local and global coordinate system of car-like robot p·d0=v·dt. (3) 为了描述机器人在平面中的位置,建立全局坐 标系X,OY,和机器人局部坐标系XgMYR,选择后轴 中点M,作为局部坐标系的原点.在全局坐标系中, M,由(x,y,)确定,M(x,y)为前轴中点坐标.在 X,OY,中M,和M的坐标关系为 ∫y=x,+lco80, (1) Lys =y,lsin 0. 全局和局部参考系之间的角度差为(0为机器 图3机器人瞬时沿圆周运动 人的航向角),令=[x,y,0]为机器人在全局参 Fig.3 The circumferential movement system track of the 考系中的位姿.用正交旋转矩阵R(0)将全局参考 robot 系X,OY,映射到局部参考系XMYR中,即= 另在直角三角形内有p=l/amp,pr=l/sinp,从 R(0)E,反之则有E=R(0). 式中: 而可得d0=业-“吧,盟=只.同理 P. cos 0 sin0 07 R(0) = sin c080 0, 可得-血巴此时=[g,09,], dt 0 1 [v cos ysin 「cos0-sin00 巴,M,在全局坐标系 R(0)-4 sin 0 c0s00 X,OY中的位姿状态方程为 L 0 0 1J sin0 0- 机器人局部坐标系如图2所示,1为轴距,”为 :=R(0) sin 0 cos 0 车轮转向角,d为轮距,ICR(instantaneous center of 0 0 1 rotation)为瞬时转动中心).设M,、M的瞬时转弯 [,0 , ano], (4) 半径分别为p,Pr 1 即 5=[v,cos 0 v,sin 0 tan o]'. (5) M在全局坐标系中的位姿状态方程为 -cos 0 sin 00- =R(0) = sin 6 cos 0 0 L 0 0 1/ [vcos vsin 2 (6) ICR 即 图2机器人局部坐标系 Fig.2 Local coordinate system of the robot 号=[c(0+p)ysin(0+p)号inpj (7)

·536. 智能系统学报 第4卷 将式(2)代入(7)得 际运动过程中,转向角中保持不变时做圆周运动. =[,cos(0+22 sin(0+) 在仿真过程中,”取为时间t的函数p(t),机器人运 cos cos 名tanoJ. 动的轨迹图如图5所示,分别代表了前后轮轴中点 (8) 的运动轨迹。 此时,分别建立起M,和M的状态方程(5)和 1..... 前轴轨迹 (8),都与0、p、,有关 后轴轨迹 2阿克曼约束的机器人运动模型 起点 四轮车辆的理想模型中,实际上是将前面的2 个轮子看成了一个轮子在运动,如图4所示.在实际 的车式移动机器人转向过程中,为了使所有车轮都 处于纯滚动而无滑动,要求转向轴内、外轮转角之间 终点 符合阿克曼原理山.令2为内轮的相对转向角,p, 为外轮的相对转向角.为了实现转向时转向车轮的 图5机器人的运动轨迹图 纯滚动,不发生横向滑移,4个车轮应绕ICR转动, Fig.5 Movement track of the robot 并且内外轮转角之间应该满足式(9)10: 图6中所示为虚拟转向角φ与实际车辆转向角 p1、p2间的关系图.p1与p2的变化趋势较为一致, cotp,-coto2=P,+2-P,-,2=4.(9) 据式(9)可得cotp1-cotp的理论值为0.5556,实 际仿真结果值为0.5505,误差在可接受范围内. 可以解得 4 「cotp1=cotp+d/2l, (10) Lcot 2 cot o -d/21. 020406080100120140160 t/s 图6转向角p1P2p间的关系 Fig.6 Tumning angles ,2 and 图7反映了转向角”与航向角0的关系,航向 角0大致可分为4个阶段,如图中A、B、C标记所 示.初始阶段随着”的变化0逐渐增大,当φ向相 ICR 反方向逐渐变大时,0在点A处才开始逐渐变小.在 图4基于阿克曼原理的机器人运动模型 A-B阶段,”的微小变化并没有影响到整车运动的 Fig.4 Kinematics modeling of car-like moblie robot based 方向;到B-C阶段,0又随着p的反向开始变化.实 on Ackerman principle 验有效地验证了该运动模型符合实际机器人转向角 设p和p分别为左右两前轮的瞬时转弯半径,得 与航向角间的关系。 p=l/sinp1,p=l/sinp2,同理可得左右后轮的瞬时转 弯半径p.=l/anp+d/2,p,=l/tanp-d/2.定义内轮 差0=p-p(左转向时为p=p-p,). 3仿真实验 在Matlab7.0上对四轮车式移动机器人的运动 学模型进行仿真实验.仿真参数为:轴距l=2.7m, 020406080100120140160 t/s d=1.5m,v,=10m/8.设初始位姿,=[00π/4], 图7转向角p和航向角0的关系 根据式(1)可得=[1.91.9π/4].机器人实 Fig.7 Truning angle o and direction 6

第6期 任孝平,等:基于阿克曼原理的车式移动机器人运动学建模 537 图8所示为航向角0与内轮差△p间的关系.从 Yuechao.Kinematics modeling and analyses of all-terrain 图中可以看出,当航向角0有较大改变时,内轮差 wheeled mobile robots[J].Chinese Journal of Mechanical 4p的变化并不明显.可见4p与0的关系并不密切, Engineering,2008,44(6):148-154. 而仅与转向角p、P2的变化有关,这点从△p的数学 [5]TLALE N,DeVILLIERS M.Kinematics and dynamics mod- 公式上也可分析出. elling of a mecanum wheeled mobile platform[C]//15th In- terational Conference on Mechatronics and Machine Vision 600 400 in Practice (M2VIP08).Auckland,New-Zealand,2008: 200 内轮差 657-662. -200 [6]MUIR P F,NEUMAN C P.Kinematic modeling of wheeled =40 -600 0 50 100 T50 mobile robots CMU-RI-TR-86-12 R].Robotics Institute, t/s (a)内轮差△p Caregie Mellon University,1986. [7]周文琴,贾英民.4轮操纵车辆改进的自适应控制[C]// 航向角 2002中国控制与决策学术年会论文集.沈阳,2002:168 171. ZHOU Wenqin,JIA Yingmin.Improvement adaptive control 20406080100120140160 of 4WS car[C]//2002 Proceedings of Chinese Control and T/S (b)内轮差0 Decision Conference.Shenyang,2002:168-171. [8]邓召文,张福兴.基于转向半径的汽车稳态转向特性分 图8航向角8和内轮差△p对比图 析J].农业装备与车辆工程,2007(1):23-26. Fig.8 Direction 0 and inner-tyre minus Ap DENG Zhaowen,ZHANG Fuxing.The analysis of steady- 4结束语 state steering characteristic turing radius-based in vehicle [J].Agricultural Equipment Vehicle Engineering,2007 本文首先分析了四轮车式移动机器人的运动特 (1):23-26. 性,建立了不考虑滑行、刹车等的四轮机器人理想运 [9]MORETTE N,NOVALES C,VIEYRES P.Inverse versus 动学模型.向该理想运动学模型引入了阿克曼约束, direct kinematics model based on flatness and escape lanes 同时对描述机器人运动状态的转向角、航向角和转 to control CyCab mobile robot[C]//2008 IEEE Interation- 向半径等物理量进行了分析.通过仿真分析了左前 al Conference on Robotics and Automation.Pasadena,CA. 轮转向角”,和右前轮转向角P2和理论转向角P之 USA,2008:2240-2245. 间的关系以及转向角φ和航向角0的关系.实验验 [10]RATNER D,MCKERROW P.Dynamics of the Titan four- wheel drive mobile robot with floating Ackerman steering 证了所建立的运动学模型的正确性,为进一步研究 [C]//Brisbane,1999:144-149. 四轮车式机器人的运动控制系统设计、自主导航等 [11]孟刚.车辆的转向特性与阿卡曼转向原理的分析 工作提供了理论分析的基础。 [J].机械研究与应用,2007,20(4):36-38. 参考文献: MENG Gang.Analysis of turning characteristic and the principle of Ackerman turning for vehicleJ].Mechanical [1]REN Xiaodong,FENG Zuren,CHANG Hong,MU Ruofeng. Research Application,2007,20(4):36-38. Kinematics modeling and analysis for three-wheel omnidirec- 作者简介: tional mobile robot [C]//Proceedings of the 7th World Con- 任孝平,男,1984年生,博士研究 gress on Intelligent Control and Automation.Chongging,Chi- 生,主要研究方向为多机器人系统、通 na,2008:2608-2613. 信网络等,发表学术论文10余篇. [2]SIEGWART R,NOUBAKHSH I R.Introduction to autono- mous mobile robots[M].MA.USA:MIT Press,2004:202- 205. [3]CHEN Lei,MA Jie,GAO Haibo.Kinematics modeling of eight-wheel lunar rover[C]//Proceedings of the 27th Chi- 蔡自兴,男,1938年生,教授、博士 nese Control Conference.Kunming,China,2008:346-350. 生导师,国际导航与运动控制科学院 [4]宋小康,谈大龙,吴镇炜,王越超.全地形轮式移动机器 院士、中国人工智能学会副理事长、中 人运动学建模与分析[J].机械工程学报,2008,44(6): 国自动化学会理事.主要研究方向为人 148-154 工智能、机器人、智能控制,发表学术论 SONG Xiaokang,TAN Dalong,WU Zhenwei,WANG 文500余篇