
第5卷第1期 智能系统学报 Vol.5 No.1 2010年2月 CAAI Transactions on Intelligent Systems Feb.2010 doi:10.3969/i.issn.1673-4785.2010.01.007 基于集对分析的不确定性多属性决策模型与算法 赵克勤 (诸暨市联系数学研究所,浙江诸暨311811) 摘要:针对不确定性多属性决策问题,提出统计学中的样本特征参数均值和方差也是模糊数(区间数、三角模糊 数、梯形模糊数)特征参数的理论,并用联系数A+B脉表示“均值+方差”,再根据集对分析中的联系数理论计算“均 值+方差”的“模”,用这种“模”代表属性权重和属性值进行不确定性多属性决策,简便实用;利用“均值+方差”联 系数中的不同取值可以考察不确定性对排序的影响.应用实例表明该理论是有效和可行的. 关键词:不确定性;多属性决策;模糊数;联系数;集对分析 中图分类号:TP18文献标识码:A文章编号:16734785(2010)010041-10 Decision making algorithm based on set pair analysis for use when facing multiple uncertain attributes ZHAO Ke-qin Institute of Zhuji Connection Number,Zhuji 311811,China) Abstract:To help those making decisions when faced with multiple uncertainties,a theory was put forward that in statistics,the average and variance of characteristic parameters of a sample have the characteristic parameters of a fuzzy number.This includes interval number,triangular fuzzy number,and trapezoidal fuzzy number.Average variance was shown as a connection number A+Bi.The modular of average variance was then calculated accord- ing to connection number theory in set pair analysis.The module,representing the weight and value of attributes, can be employed to help make decisions when there are multiple uncertain attributes.The method is simple and practical.Taking various values of i,the effect of uncertainty on sorting can be determined.Practical examples were used to demonstrate the feasibility and effectiveness of the proposed theory. Keywords:uncertainty;multiple attribute decision making;fuzzy number;connection number;set pair analysis 多属性决策是科学技术及社会经济领域中相当 虽然各有特色而且有效,但另一方面,由于不同算法 广泛的一类决策问题.也是智能决策中的常见问题. 之间互有交集,也使得决策时难以适从;从科学研究 当属性权重与属性值都是确定的实数时,已有许多 的角度看,需要对不同的算法探讨其中共性的规律. 成熟的算法;当属性权重与属性值含有一定程度的因而讨探具有一定普适意义的不确定性多属性决策 不确定性时,相应的算法还在探讨之中.这些算法大 新算法仍显得十分重要,集对分析是站在确定性与 致可分为基于模糊集理论的算法和基于概率统计的 不确定性对立统一哲学角度建立起来的一种新的不 算法2大类,其中基于模糊集理论的算法又分为基 确定性系统理论1o21,近年来在不确定性多属性决 于区间数的多属性决策算法「12]、基于三角模糊数 策研究中也崭露头角.例如文献[13-14]把集对分析 的多属性决策算法34]、以及基于梯形模糊数的多 的同异反联系数用于区间数多属性决策;文献[15- 属性决策算法56这样3个子类,每个子类算法又分 17]把集对分析的二元联系数用于区间数多属性决 别结合地应用TOPSIS(technique for order preference 策;文献[18]把二元联系数用于三角模糊数多属性 by similarity to ideal solution)方法r、灰色理论[8] 决策等等.事实上,根据集对分析的不确定性系统理 AHP(analytic hierarchy process)法[9]等等.这些算法 论,可以把模糊集理论和概率统计理论在一定条件 下统一起来加以研究.基于这一理念,并在文献[15 收稿日期:20090601. 通信作者:赵克勤.E-mail:对zhaok@sohu.com, 18]的基础上,提出统计学中的样本特征参数“均

42 智能系统学报 第5卷 值”和“方差”也是模糊数(区间数、三角模糊数、梯 形模糊数)特征参数的观点,并用联系数A+Bi表示 (-)2 (为-x)2 “均值+方差”这种特征参数,再根据集对分析(st n-1 2 pair analysis,.简记为SPA)中的联系数理论把 (x-x)2+(xM-)2+(x-x) (5) “均值+方差”转换成D-U空间中的三角函数表达 式.在此基础上给出不确定性多属性决策的“主值 作为三角模糊数x=[x,x“,x]的特征参数是合理 模型”和“一般模型”,其中的“主值模型”仅涉及到 的.因为至少从统计学的样本意义上说明了三角模 “均值+方差”的“模”的计算,用这种“模”代表属 糊数的集中性(确定性)与离散性(不确定性). 性权重和属性值进行不确定性多属性决策,得到了 1.3梯形模糊数的特征参数 与其他算法相同的结果,算法相对简便;“一般模 记R为实数域,称 型”则通过联系数中的不同取值考察不确定性对 x=[x,x",x",x"] (6) 方案排序稳定性的影响,从而为不确定性多属性决 是一个梯形模糊数,其中0<x<xM<x<x”∈R, 策问题给出了既便于实际应用也适合智能机处理的 且称x、x”为梯形模糊数的下确界和上确界,称区 间[x“,x]为梯形模糊数的中值区间. 一种统一算法。 显然,若把x、x“、x、x”看成是同一对象X的4 1均值和方差也是模糊数的特征参数 个观察值(忽略不计x、x“、x、x”出现的先后),那 么,这4个观测值的平均值 1.1区间数的特征参数 1 记R为实数域,称闭区间[x,x+]为区间数, x= 与=+++ (7) n 记为x=[x,x*],其中xeR,x∈R,x≤x*. 与方差 显然,若把xˉ、x*看成是同一对象X的2个观 察值(忽略不计x、x+出现的先后),那么,把这2 (-)2 (-x)2 个观测值的平均值 n-1 3 =1公两=2 (x+x) (1) (x-x)2+(xM-x)2+(xW-x)2+(x”-x) n 与方差 (8) 作为梯形模糊数x=[x,xM,x,x”]的特征参数是 ∑(-)2 2 合理的,因为至少从统计学的样本意义上说明了梯 n-1 形模糊数的集中性(确定性)与离散性(不确定性). √(x-x)2+(x*-x) (2) 2均值和方差的集对分析 作为区间数x=[xˉ,x+]的特征参数是合理的.因 为至少从概率统计学的样本意义上1说明了区间 根据集对理论,均值x和方差s既然是反映同 数的集中性(确定性)与离散性(不确定性)· 一对象X的n(n≥2)个观察值的2个特征参数;因 1.2三角模糊数的特征参数 而可以看作是关于对象X的有联系的2个集合,并 记R为实数域,称 组成集对H=(x,s)其中的均值x又可以看作是关 =[x,] (3) 于对象X的n(n≥2)个观察值的相对确定性(严格 是一个三角模糊数,其中0<x<x“<x"∈R,且称 说是集中性)的测度,方差s是关于对象X的n(n≥ x、x分别为三角模糊数的下确界和上确界,x“为 2)个观察值相对不确定性(严格说是离散性)的测 三角模糊数的中值. 度.集对H=((x,s)因此是一个确定-不确定集对,可 显然,若把x、x“x看成是同一对象X的3个 以用集对分析中的联系数A+B:表示均值x和方差 观察值(忽略不计x、x“、x出现的先后),那么,把 s的相互关系。 这3个观测值的平均值 定义1设x和s分别是同一对象X的n(n≥ 2)个观察值的平均值和方差,则称 (4) u(x,s)=A+Bi(A=x,B=s,i∈[-1,1])(9) 与方差 或

第1期 赵克勤:基于集对分析的不确定性多属性决策模型与算法 ·43 u(x,s)=x+si(i∈[-1,1]) (10) 0=arctan s (17) 中的u(x,s)为对象X的n个观察值的均值-方差联 系数,简称均值-方差联系数或直称联系数. 为均值-方差联系数u(x,s)在集对分析二维D-U空 均值-方差联系数u(,s)中的均值x和方差s 间中的幅角,称式(17)为均值-方差联系数u(x,s) 的相互作用则可以映射到基于集对分析的二维确 的幅角公式,记为argu(x,s). 定-不确定空间[(determination-ncertain,简称D-U 3均值-方差联系数的运算 空间)作进一步分析.如图1、2所示,其中的y轴表 示相对不确定性测度,x轴表示相对确定性测度. 3.1普通运算 由于均值-方差联系数u(x,s)在形式上就是集对 分析中的二元联系数A+Bi,因此其普通运算就是二 元联系数A+B的普通运算0,为此可以在不计不 0 确定性层次的条件下,对i的运算遵循以下规则: i=花=流=…=”,n=1,2,…,k.(18) 图1D-U空间 Fig.1 D-U space 据此可以使运算结果仍然为形为A+Bi或x+ s形式的联系数, 4=T+S 3.2加法运算 若山1(x1,51)=x1+51i,山2(x2,2)=x2+2i,则 山1(1,1)+山2(2,52)= (x1+2)+(s1+s2)i. (19) 图2H=(x,)在D-U空间上的映射 由(19)式易知2个均值-方差联系数u(x,s)的加法 Fig.2 The mapping of H=(,s)on the D-U space 运算满足交换律,也就是 由图2看出,均值-方差联系数u(x,s)中的x、s u1(x1,s1)+42(x2,2)= 在D-U空间中存在相互协同作用,其相互协同作用 2(2,52))+41(1,s1). (20) 的空间映像是从原点O指向U的向量OU,该映像 3个或更多个均值-方差联系数相加的运算还 的大小即相互协同作用的大小,也就是向量OU的 满足加法结合律: “模”,记为 山1(x1,1)+山2(x2,2)+山3(x3,3)= r=|0U1=√e2+s (11) 41(,s1)+[山2(名,2)+4(,3)].(21)》 0表示均值-方差联系数u(x,s)经映射后得到的向 证明略. 量OU与x轴正向的夹角.由图2易知: 3.3n个均值-方差联系数的平均 x=rcos 0, (12) 记n个均值-方差联系数山1(x1,s1),山2(2,s2), y rsin 6. (13) …,4n(xn,sn)的平均均值-方差联系数为u(x,s)= 于是,有 元+,则有 u(x,s)=r(cos 0 isin 0). (14) u(,)=14(4)=1(4+)= n n 式(14)称为均值-方差联系数u(x,s)在集对分析二 维D-U空间中的三角函数表达式, L∑+n (22) n n台 为明确起见,以下给出均值-方差联系数u(x, 3.4乘法运算 s)的模以及幅角的定义, 设有均值-方差联系数山1(名1,s1)=x1+s1i, 定义2设有均值-方差联系数u(x,s),则称 山1(x2,52)=x2+2i,山1(x1,s1)与山2(x2,2)的乘积 r=√e+s (15) 为u(x,s),则 为均值-方差联系数u(x,s)在集对分析二维D-U空 u(x,s)=[41(x1,s1)][42(x2,2)]= 间中的模.称式(15)为u(x,s)求模公式,记为 +i+i+siszi. (23) r=|u(x,s)1. (16) 根据式(18),可简化式(23)得 定义3设有均值-方差联系数u(x,s),则称 [u1(x1,s1)][山2(x2,s2)]=

44 智能系统学报 第5卷 (x1x2)+(x12+251+s1s2)i (24) 为Pu(k=1,2,…,m),权重0,与评价值P各为模 式(24)也称为均值-方差联系数乘法公式, 糊数(区间数、三角模糊数、梯形模糊数)或“均值+ 均值-方差联系数乘法与加法的混合运算满足: 方差”的特征参数,决策矩阵为P=(P)mxm,(k= 1)交换律: 1,2,…,m,t=1,2,…,n),假定属性Pa已经过规范 [山1(x1,1)][2(x2,S2)]= 化处理为越大越好型,规范化处理后的属性决策矩 [u2(x2,s2)][u1(1,s1)] (25) 阵为R=(Tu)mxa 2)结合律: 要求对m个方案中决策出最优方案,并对这些 [山1(x1,s1)][2(2,s2)][4(,3)]= 方案作出从优到劣的排序, [u1(,s1)]{[2(,2)][山(,3)]}.(26) 4.2决策模型 3)分配律: 4.2.1基本模型 [山(x1,s1)][2(x2,2)+山3(x3,s3)]= 设方案S(k=1,2,…,m)的各属性权重为0, [山1(x1,s1)][山2(x2,52)]+ 属性值为P(t=1,2,…,n),其综合评价结果为 [山1(元1,s1)][4(3,3)]. (27) M(S),则有 显然,根据上面相应的运算规则,易证式(25)、 (26)、(27)成立,证明略。 M(S)= (31) 3.5均值-方差联系数三角函数式的运算 式(31)称为不确定性多属性决策加权综合基本模 设 型,其值称为加权综合值,或简称基本值 u1(1,s1)=r1(co801+i8in0), 由基本值M(S)(k=1,2,,m)构成的矩阵: 42(x2,s2)=r2(c0s02+i8in02). M(S:)=[M(S)M(S2)M(S3)M(S:) 这时2个均值-方差联系数的乘法运算公式为 称为方案的加权综合基本值决策矩阵,有时也不加 山1(x1,51)山2(x2,52)= 区分地用M(S)表示,以下类同. r (cos 0 isin 0)r2 (Cos 02 isin 02)= 4.2.2一般综合模型 rr2[cos(01+02)+i8in(01+02)].(28) 把式(31)中的权重0,与属性值P.各自转换成 从而有 均值-方差联系数“(x,s)的三角函数表达式,即 1山1(1,s1)山2(2,52)1= 0,=Tm,(cos0。,+isin0), |山1(x1,s1)11h2(2,52)1=T1T2, (29) arg[w1(x1,s1)2(x2,s2)]= Du =Tp (cos isin on ) 其中均值-方差联系数u(x,s)的模和幅角由式 arg[山1(x1,s1)]+arg[2(名,s2)].(30)) 也就是说:2个用三角函数表示的均值-方差联系数 (16)、(17)确定,则有 u(x,s)相乘,结果仍是形如x+si的均值-方差联系 数,且乘积的模等于这2个联系数模的乘积,乘积的 Ms)=.e(a,+8)+ (32) 辐角等于它们辐角的和. isin(0,.+0)]. 以上仅就本文涉及的均值-方差联系数u(x,s) 式(32)称为基于集对分析的不确定性多属性 运算作了介绍,进一步的运算可以参照文献[18]. 决策一般综合模型,其值称为SPA综合决策值,也 有关均值-方差联系数u(x,s)运算的统计学意义也 简称一般综合值.称式 将另文讨论. Tm'p[cos(0+0p)+isin(0,+0)](33) 为一般综合值的分量,M(S)为方案的综合一般值 4基于均值-方差联系数的不确定性 决策矩阵, 多属性决策模型与算法 4.2.3主值模型 4.1问题描述 当式(32)中的[cos(0。.+8,.)+isin(,+ 设有m个方案:S1,S2,…,Sm;每个方案各有n 0)]=1时,得 个属性:Q1,Q2,…,Q.,每个属性的权重0,(t=1,2, Ms)=5 (34) …,n)且∑0,=1,第k个方案第t个属性的评价值 称式(34)为基于集对分析的不确定性多属性

第1期 赵克勤:基于集对分析的不确定性多属性决策模型与算法 ·45 决策综合主值模型,简称综合主值决策模型或主值 3)利用均值-方差联系数模及幅角的计算公式 模型,也称为“模”模型;其值称为综合决策主值,也 把决策问题中的各属性权重与属性值改写成三角函 简称主值或模值.称'为综合主值的分量,M 数表达式 (S)为方案的综合主值决策矩阵或简称模矩阵. 4)利用基于集对分析的综合主值决策模型 4.2.4决策步骤 式(34),计算各方案的综合主值,主值大的方案优 1)先把决策问题中给出的属性值作规范化处理, 先于主值小的方案. 当属性值P表示第k个方案在t个属性上的评 5)如果同一决策问题已有采用其他方法所得 价值是区间数,即P=[P,Pt](k=1,2,…,m) 结果,则把上面所得结果与其他方法所得结果相比 时,规范化公式为 较,完全一致时,可作出决策结论;不完全一致时,或 对于效益型属性值,经规范化后的区间数为 者需要考虑属性权重和属性值的不确定性对方案排 =[P,p店] 序稳定性的影响,则进入下一步. I max pi max pi 6)利用一般综合决策模型式(32)计算各决策 [x%],k=1,2,…,m (35) 方案的一般综合值时,建议其中的按比例取值原 对于成本型属性值,经规范化后的区间数为 理取值,计算公式为 co8(0+02) 「min Pk min p xp6= i=c0s(0,+0)+sim(0,.+0) (41) 有时也可以分别取i=-0.5,i=0,i=0.5等这些特 [x],k=1,2,…,m,Pa≠0. (36) 殊值,以考察由不确定性引起的一般综合值的变化 当属性值P,表示第k个方案在t个属性上的评 及对决策方案排序的影响. 价值是三角模糊数,即Pa=[p,p,p](k=1,2, …,m,t=1,2,…,n)时,规范化公式为 5应用举例 对于效益型属性值,经规范化后的三角模糊数为 5.1在区间数多属性决策中的应用 -小 例1考虑某所大学的5个学院(S1,S2,S3,S4, S5)的综合评估,假定采用教学、科研和服务3个属 [%,,0],k=1,2,…,m; (37) 性作为评估指标,各属性的权重和决策矩阵见表1, 对于成本型属性值,经规范化后的三角模糊数为 试做出综合评估和排序[21 「minpmin p min p购]= 表15个学院的区间数决策矩阵和属性权重 Table 1 Five colleges interval numbers decision matrix and [x,x数,x如],k=1,2,…,m,p≠0.(38) attribute weight 当属性值P:表示第斥个方案在t个属性上的评 教学Q1 科研Q2 服务Q3 价值是梯形模糊数,即Pa=[p,P“,P如,P](k=1, 学院 01= 现2 03= 2,…,m,t=1,2,…,n)时,规范化公式为 [0.3350,0.3755][0.3009,0.3138][0.3194,0.3363] 「0.214.0.2201 [0.166,0.178] [0.184,0.190] 对于效益型属性值,经规范化后的梯形模糊数为 =,,心,= S2 [0.206,0.225] [0.220,0.229] [0.182.0.191] S3 [0.195,0.204] [0.192,0.198] [0.220,0.231] max p max pa'max pa'maxpl U [0.181,0.190] [0.195,0.205] [0.185,0.195 [xk,x,x0,x0],=1,2,…,m;(39) S [0.175,0.184] [0.193,0.201] [0.201,0.211] 对于成本型属性值,经规范化后的梯形模糊数为 解:步骤1):先按综合主值决策模型式(34)处 min P min p min pi min pe 理如下: *pu= 「Ip,p,p,pk可 a)由于教学、科研和服务这3个属性都是越大 [x点,x,x0,x],k=1,2,…,m,P≠0.(40) 越好的效益型属性,且题给出的各属性值已作无量 2)计算规范化后的各属性权重和属性值的特 纲的规范化处理,所以可以直接应用式(1)和式(2) 征参数均值x和方差s,写成均值-方差联系数 计算权重区间数和决策矩阵中的各属性值区间数的 u(x,s)的形式 均值-方差联系数得表2
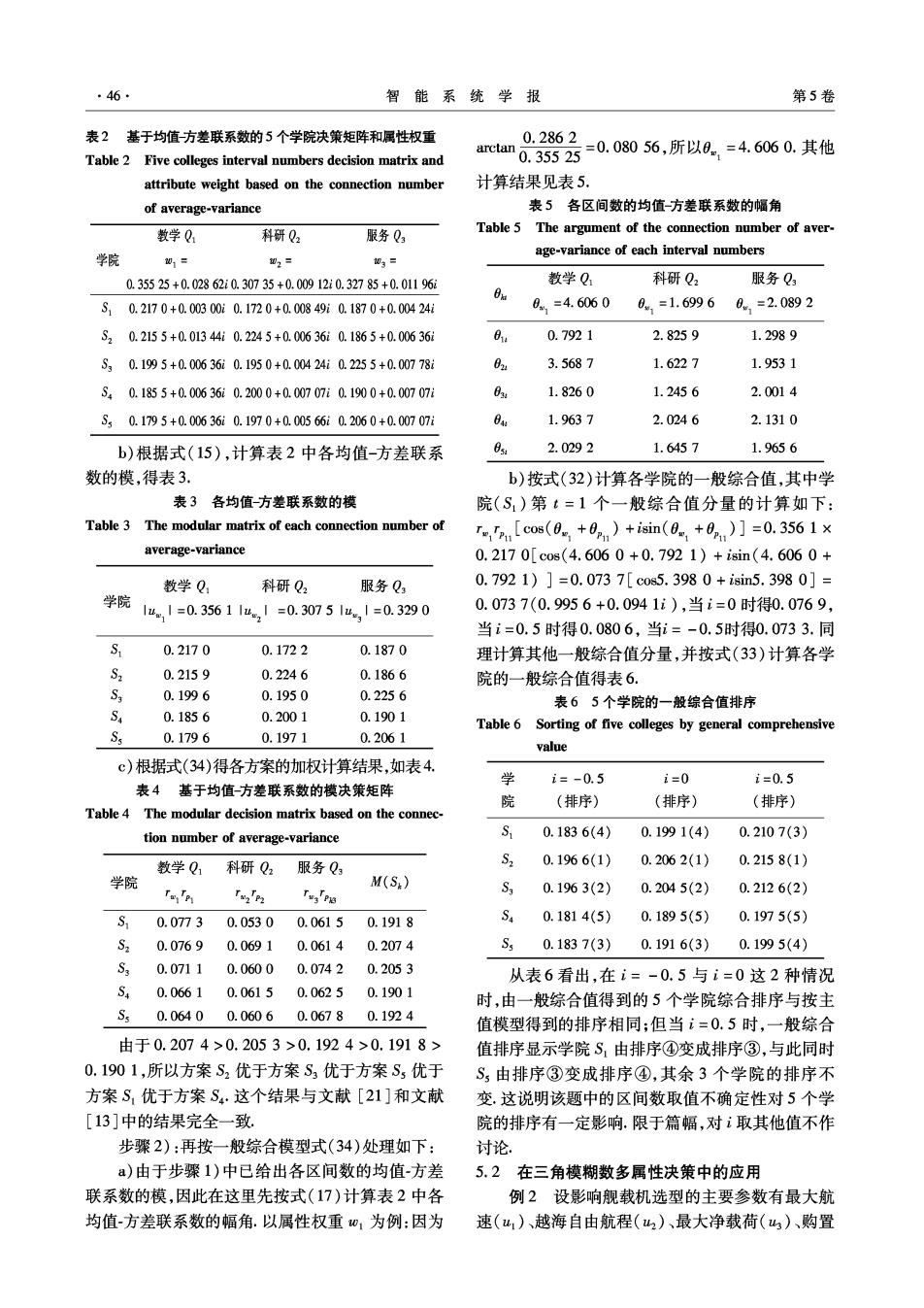
46 智能系统学报 第5卷 表2 基于均值-方差联系数的5个学院决策矩阵和属性权重 arctan Table 2 Five colleges interval numbers decision matrix and 0.2862=0.08056,所以0,=4.6060.其他 0.35525 attribute weight based on the connection number 计算结果见表5 of average-variance 表5各区间数的均值-方差联系数的幅角 教学Q 科研Q2 服务Q3 Table 5 The argument of the connection number of aver- 学院 age-variance of each interval numbers 01= 02= 03= 0.35525+0.02862i0.30735+0.00912i0.32785+0.01196t 教学Q1 科研Q2 服务Q3 S10.2170+0.00300i0.1720+0.00849i0.1870+0.00424i 81=4.6060 81=1.6996 8=2.0892 S20.2155+0.01344i0.2245+0.00636i0.1865+0.00636i 0.7921 2.8259 1.2989 S30.1995+0.00636i0.1950+0.00424i0.2255+0.00778i 02 3.5687 1.6227 1.9531 S40.1855+0.00636i0.2000+0.00707i0.1900+0.00707i B3 1.8260 1.2456 2.0014 S0.1795+0.00636i0.1970+0.00566i0.2060+0.00707i 64射 1.9637 2.0246 2.1310 b)根据式(15),计算表2中各均值-方差联系 0s 2.0292 1.6457 1.9656 数的模,得表3. b)按式(32)计算各学院的一般综合值,其中学 表3各均值-方差联系数的模 院(S,)第t=1个一般综合值分量的计算如下: Table 3 The modular matrix of each connection number of 'n.[cos(0+0,n)+isin(0,+0,)]=0.3561× average-variance 0.2170[c0s(4.6060+0.7921)+isin(4.6060+ 数学Q 科研Q2 服务Q 0.7921)]=0.0737[cos5.3980+isin5.3980]= 学院 1um,1=0.356114,=0.3075143=0.3290 0.0737(0.9956+0.0941i),当i=0时得0.0769, 当i=0.5时得0.0806,当i=-0.5时得0.0733.同 6 0.2170 0.1722 0.1870 理计算其他一般综合值分量,并按式(33)计算各学 S2 0.2159 0.2246 0.1866 院的一般综合值得表6. S 0.1996 0.1950 0.2256 表65个学院的一般综合值排序 S 0.1856 0.2001 0.1901 Table 6 Sorting of five colleges by general comprehensive 0.1796 0.1971 0.2061 value c)根据式(34)得各方案的加权计算结果,如表4. 学 i=-0.5 i=0 i=0.5 表4基于均值方差联系数的模决策矩阵 院 (排序) (排序) (排序) Table 4 The modular decision matrix based on the connec- tion number of average-variance S 0.1836(4) 0.1991(4) 0.2107(3) 数学Q1科研Q2服务Q S2 0.1966(1) 0.2062(1) 0.2158(1) 学院 M(S;) T T2'2 Tws'na S3 0.1963(2) 0.2045(2) 0.2126(2) S 0.07730.05300.0615 0.1918 0.1814(5) 0.1895(5) 0.1975(5) S2 0.07690.0691 0.0614 0.2074 0.1837(3) 0.1916(3)0.1995(4) S30.07110.0600 0.0742 0.2053 从表6看出,在i=-0.5与i=0这2种情况 S40.06610.06150.0625 0.1901 时,由一般综合值得到的5个学院综合排序与按主 S50.06400.06060.0678 0.1924 值模型得到的排序相同;但当i=0.5时,一般综合 由于0.2074>0.2053>0.1924>0.1918> 值排序显示学院S,由排序④变成排序③,与此同时 0.1901,所以方案S2优于方案S3优于方案S5优于 S由排序③变成排序④,其余3个学院的排序不 方案S,优于方案S4·这个结果与文献[21]和文献 变.这说明该题中的区间数取值不确定性对5个学 [13]中的结果完全一致. 院的排序有一定影响.限于篇幅,对i取其他值不作 步骤2):再按一般综合模型式(34)处理如下: 讨论 a)由于步骤1)中已给出各区间数的均值-方差 5.2在三角模糊数多属性决策中的应用 联系数的模,因此在这里先按式(17)计算表2中各 例2设影响舰载机选型的主要参数有最大航 均值-方差联系数的幅角.以属性权重w1为例:因为 速(u1)、越海自由航程(2)、最大净载荷()、购置

第1期 赵克勤:基于集对分析的不确定性多属性决策模型与算法 ·47… 费(山4)、可靠性(山5)、机动灵活性(6)6项指标,现 02=[0.10,0.125,0.15], 有4种机型(1,2,3,4)可供选取择,专家给出的 03=[0.10,0.125,0.15], 各指标权重w,((t=1,2,·,6)和各指标的评价值矩 04=[0.10,0.125,0.15], 阵R用三角模糊数形式表示如下2): 05=[0.19,0.21,0.23], 01=[0.15,0.17,0.19], 06=[0.23,0.24,0.25]. /[0.78,0.80,0.85][0.92,0.95,1.00][0.70,0.72,0.78][0.85,0.88,0.90] [0.50,0.55,0.58][0.95,0.97,1.00][0.72,0.74,0.75][0.65,0.67,0.70] R= [0.90,0.95,0.95][0.85,0.86,0.88][0.95,0.98,1.00][0.90,0.95,0.96] [0.80,0.82,0.85][0.65,0.69,0.71][0.94,0.97,1.00][0.85,0.90,0.93] [0.45,0.50,0.57][0.17,0.20,0.23][0.80,0.83,0.85][0.46,0.50,0.52] [0.90,0.95,0.97][0.47,0.51,0.55][0.80,0.82,0.85][0.48,0.50,0.52] 解:1)根据式(4)和式(5),计算各属性权重三17+0.0141i,02=0.1250+0.0177i,w3= 角模糊数和决策矩阵中的三角模糊数的特征参数均0.1250+0.0177i,04=0.1250+0.0177i,05= 值和方差,写出相应的均值-方差联系数得:w1=0.0.21+0.0141i,06=0.24+0.0071i. 0.8100+0.0255i,0.9567+0.0286i,0.7333+0.0294i,0.8767+0.0178i 0.5433+0.0286i,0.9733+0.0178i,0.7367+0.0108i,0.6733+0.0218i R'= 0.9333+0.0240i,0.8633+0.0108i,0.9767+0.0178i,0.9367+0.0227i 0.8233+0.0000i,0.6833+0.0432i,0.9700+0.0212i,0.8933+0.0286i 0.5067+0.0426i,0.2000+0.0212i,0.8267i+0.0178i,0.4933+0.0216i 0.9400+0.0255i,0.5100+0.0283i,0.8233+0.0178i,0.5000+0.0141i 2)根据式(15),计算各属性权重均值-方差联 A2=[0.8891,0.9154,0.9492,0.9772], 系数和R'中各均值-方差联系数的模,得 A3=[0.8647,0.8945,0.9231,0.9537], 1ug1=0.1706,14m,1=0.1262, A4=[0.8650,0.8986,0.9392,0.9707], 1,1=0.1262,14,=0.1262, A5=[0.8517,0.8885,0.9220,0.9560]. 1“,1=0.2105,14。=0.2401. 试从梯形模糊数越大越好的角度作出综合排序[] 解:先根据式(7)、式(8)计算得各方案的梯形 /0.8104,0.9571,0.7339,0.8769 模糊数的均值x和方差s(k=1,2,3,4,5),并写成 0.5440,0.9735,0.7367,0.6737 均值-方差联系数(x4,)(k=1,2,3,4,5),再按 R"= 0.9335,0.8634,0.9769,0.9370 式(15)、式(16)计算各均值-方差联系数的模r= 0.8233,0.6847,0.9702,0.8938 I,(k,s)|,根据模的大小得各方案优劣排序结果 0.5085,0.2011,0.8269,0.4938 (见表7). 0.9403,0.5108,0.8235,0.5002 表75个方案的均值-方差联系数的模及其排序 3)根据式(34)得各方案的加权计算结果: Table 7 Sorting of five schemes based modular of connec- M(S.,)=0.7614,M(S)=0.6465, tion number of average-variance M(S,)=0.8357,M(S,)=0.6879. 方案 山(,) 排序 也就是机型3优于v1优于4优于2,这一结果与 A 0.8887+0.0371i 0.8895 ⑤ 文献[22]所得结果完全一致. A 0.9327+0.0338i 0.9333 ① 5.3在梯形模糊数多属性决策中的应用 As 0.9090+0.0332i 0.9096 ③ 例3已知A、A2、A3、A4、A5个方案,经群决 A0.9184+0.0400i0.9193 ② 策综合后的评价结果用梯形模糊数表示为 40.9046+0.0387i0.9054 ④ A1=[0.8409,0.8699,0.9043,0.9398], 所得各方案的排序结果与文献[23]完全一致
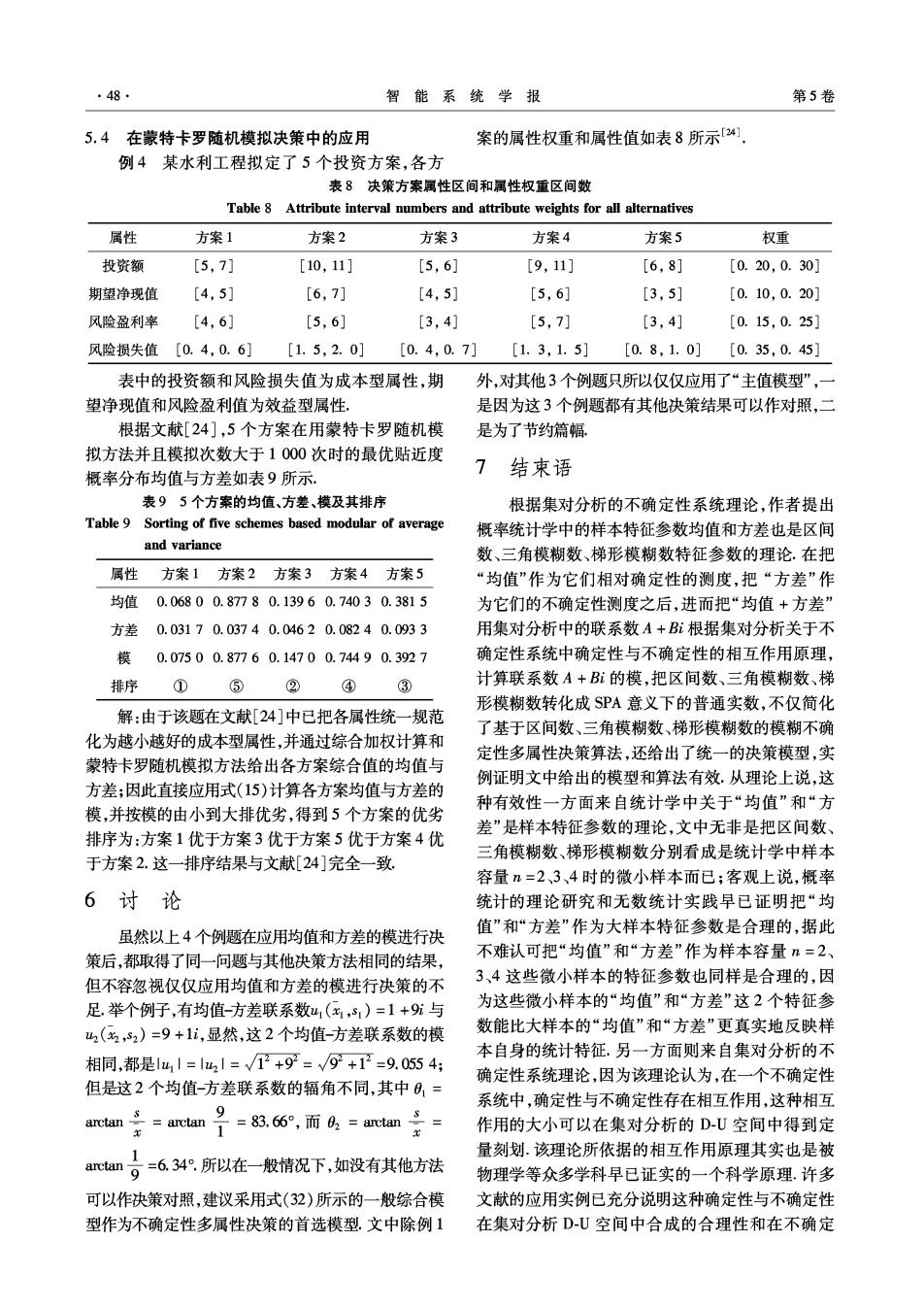
48 智能系统学报 第5卷 5.4 在蒙特卡罗随机模拟决策中的应用 案的属性权重和属性值如表8所示[4] 例4某水利工程拟定了5个投资方案,各方 表8决策方案属性区间和属性权重区间数 Table 8 Attribute interval numbers and attribute weights for all alternatives 属性 方案1 方案2 方案3 方案4 方案5 权重 投资额 [5,7] [10,11] [5,6] [9,11] [6,8] [0.20,0.30] 期望净现值 [4,5] [6,7] [4,5] [5,6] [3,5] [0.10,0.20] 风险盈利率 [4,6] [5,6] [3,4] [5,7] [3,4] [0.15,0.25] 风险损失值[0.4,0.6] [1.5,2.0] [0.4,0.7] [1.3,1.5] [0.8,1.0] [0.35,0.45] 表中的投资额和风险损失值为成本型属性,期 外,对其他3个例题只所以仅仅应用了“主值模型”,一 望净现值和风险盈利值为效益型属性。 是因为这3个例题都有其他决策结果可以作对照,二 根据文献[24],5个方案在用蒙特卡罗随机模 是为了节约篇幅 拟方法并且模拟次数大于1000次时的最优贴近度 概率分布均值与方差如表9所示. 7结束语 表95个方案的均值、方差、模及其排序 根据集对分析的不确定性系统理论,作者提出 Table 9 Sorting of five schemes based modular of average 概率统计学中的样本特征参数均值和方差也是区间 and variance 数、三角模糊数、梯形模糊数特征参数的理论.在把 属性 方案1方案2方案3方案4方案5 “均值”作为它们相对确定性的测度,把“方差”作 均值 0.06800.87780.13960.74030.3815 为它们的不确定性测度之后,进而把“均值+方差” 方差 0.03170.03740.04620.08240.0933 用集对分析中的联系数A+B根据集对分析关于不 模 0.07500.87760.14700.74490.3927 确定性系统中确定性与不确定性的相互作用原理, 排序 ① ⑤ (② ④ ③ 计算联系数A+Bi的模,把区间数、三角模糊数、梯 形模糊数转化成SPA意义下的普通实数,不仅简化 解:由于该题在文献[24]中已把各属性统一规范 了基于区间数、三角模糊数、梯形模糊数的模糊不确 化为越小越好的成本型属性,并通过综合加权计算和 定性多属性决策算法,还给出了统一的决策模型,实 蒙特卡罗随机模拟方法给出各方案综合值的均值与 例证明文中给出的模型和算法有效.从理论上说,这 方差;因此直接应用式(15)计算各方案均值与方差的 种有效性一方面来自统计学中关于“均值”和“方 模,并按模的由小到大排优劣,得到5个方案的优劣 差”是样本特征参数的理论,文中无非是把区间数、 排序为:方案1优于方案3优于方案5优于方案4优 于方案2.这一排序结果与文献[24]完全一致. 三角模糊数、梯形模糊数分别看成是统计学中样本 容量n=2、3、4时的微小样本而已;客观上说,概率 6讨论 统计的理论研究和无数统计实践早已证明把“均 虽然以上4个例题在应用均值和方差的模进行决 值”和“方差”作为大样本特征参数是合理的,据此 策后,都取得了同一问题与其他决策方法相同的结果, 不难认可把“均值”和“方差”作为样本容量n=2、 但不容忽视仅仅应用均值和方差的模进行决策的不 3、4这些微小样本的特征参数也同样是合理的,因 足.举个例子,有均值-方差联系数u1(名,s1)=1+9i与 为这些微小样本的“均值”和“方差”这2个特征参 山2(,,2)=9+1i,显然,这2个均值-方差联系数的模 数能比大样本的“均值”和“方差”更真实地反映样 本自身的统计特征.另一方面则来自集对分析的不 相同,都是山|=1w2|=√/个+9=√92+1=9.0554: 确定性系统理论,因为该理论认为,在一个不确定性 但是这2个均值-方差联系数的辐角不同,其中0,= 系统中,确定性与不确定性存在相互作用,这种相互 arctan =acan号=83.6,而6=arctan÷= 作用的大小可以在集对分析的D-U空间中得到定 1 量刻划.该理论所依据的相互作用原理其实也是被 arctan- =6.34°所以在一般情况下,如没有其他方法 物理学等众多学科早已证实的一个科学原理.许多 可以作决策对照,建议采用式(32)所示的一般综合模 文献的应用实例已充分说明这种确定性与不确定性 型作为不确定性多属性决策的首选模型.文中除例1 在集对分析D-U空间中合成的合理性和在不确定

第1期 赵克勤:基于集对分析的不确定性多属性决策模型与算法 ·49 性多属性决策中的有效性.当然,从算法上看,在应 策方法[J].模糊系统与数学,2007,21(4):9194. 用文中所给出的均值方差联系数进行不确定性多 SUN Shiyan,WANG Hangyu,QIU Zhiming.One kind of 属性决策时,对于原始数据的规范化处理是一个前 fuzzy ELECTRE method for multi-attribute decision making 提:因为规范化后得到的属性数据,不仅消除了不同 [J].Fuzzy Systems and Mathematics,2007,21(4):91- 94. 属性的量纲,而且使不同属性得到同质化(化为越 [7]尤天慧,樊治平.区间数多指标决策的一种TOPSIS方法 大越好的效益型属性,但例4是化为越小越好的成 [J].东北大学学报:自然科学版,2002(9):840843. 本型属性),还使各属性值都落在[0,1]区间内,便 YOU Tianhui,FAN Zhiping.TOPSIS method for multiple 于计算和比较 attribute decision making with intervals[J].Joumal of 但尽管如此,人们仍会考问:应用文中给出的不 Northeastern University:Natural Science,2002(9):840- 确定性多属性决策模型与算法之有效性到底是或然 843. 的,还是必然的?是否还需要加一些限制条件和界 [8]卫贵武.区间数多指标决策问题的新灰色关联分析法 定适用范围,是否具有普遍意义?因此,文中给出的 [J].系统工程与电子技术,2006,28(9):1358-1359, 模型和算法仍然需要在理论上作进一步探讨,在应 1383. 用上作更多验证 WEI Guiwu.New method of grey relational analysis to mul- tiple attribute decision making with intervals[].Systems 参考文献: Engineering and Electronics,2006,28(9):1358-1359, 1383. [1]樊治平,尤天慧,张尧.属性权重信息不完全的区间数 [9]晏明春,郜菁.混合AHP法在ERP系统供应商评价模 多属性决策方法[J].东北大学学报:自然科学版, 型中的应用[J].计算机工程,2007,35(13):90-2, 2005,26(8):798-801 98. FAN Zhiping,YOU Tianhui,ZHANG Yao.Method for in- YAN Mingchun,GAO Jing.Application of combined AHP terval multiple attribute decision-making problem with in- in supplier evaluation model of ERP system[J].Computer complete attribute weights[J].Journal of Northeastern Uni- Engineering,2007,35(13):90-92,98. versity:Natural Science,2005,26(8):798-801. [10]赵克勤.集对分析及其初步应用[M].杭州:浙江科技 [2]徐泽水,达庆利.区间型多属性决策的一种新方法[J] 出版社,2000:44-64. 东南大学学报:自然科学版,2003,33(4):498501. [11]赵克勤.集对分析的不确定性理论在AI中的应用[J]. XU Zeshui,DA Qingli.New method for interval multi-at- 智能系统学报,2006,1(2):1625. tribute decision-making[].Joumal of Southeast Universi- ZHAO Kegin.The application of uncertainty systems theo- ty:Natural Science,2003,33(4):498-501. ry of set pair analysis (SPA)in the artiartificial intelligence [3]许叶军,达庆利.基于理想点的三角模糊数多指标决策 [J].CAAI Transactions on Intelligent Systems,2006,1 法[J].系统工程与电子技术,2007,29(9):1469- (2):16-25 1471. [12]赵克勤,宣爱理.集对论一一种新的不确定性理论方 XU Yejun,DA Qingli.Method for triangular fuzzy number 法与应用[J].系统工程,1996,14(1):1823 multiple attribute decision making based on ideal solution ZHAO Keqin,XUAN Aili.Set pair theory-A new theory [J].Systems Engineering and Electronics,2007,29(9): method of non-define and its applications[].Systems En- 1469-1471. gineering,1996,14(1):18-23 [4]陈晓红,阳熹.一种基于三角模糊数的多属性群决策 [13]叶跃样,糜仲春,王宏宇,等.一种基于集对分析的区间 方法[J].系统工程与电子技术,2008,30(2):278- 数多属性决策方法[J].系统工程与电子技术,2006, 282. 28(9):1344-1347 CHEN Xiaohong,YANG Xi.Multiple attributive group deci- YE Yuexiang,MI Zhongchun,WANG Hongyu,et al.Set- sion making method based on triangular fuzzy numbers[J. pair-analysis-based method for multiple attributes decision- Systems Engineering and Electronics,2008,30(2):278- making with intervals[J].Systems Engineering and Elec- 282. tronics,2006,28(9):1344-1347. [5]彭展声,李荣钩.模糊多属性决策的投影折衷方法[J]. [14]黄英艺,蔡光程,刘文奇.一种基于SPA的不确定多属 模糊系统与数学,2006,20(4):8690, 性决策的排序方法[J].昆明理工大学学报:理工版, PENG Zhansheng,LI Rongjun.Projected compromise meth- 2008,33(6):113-116 od for fuzzy multiple attribute decision making[J].Fuzzy HUANG Yingyi,CAI Guangcheng,LIU Wenqi.A ranking Systems and Mathematics,2006,20(4):86-90 approach based on set-pair-analysis in uncertain multiple [6]孙世岩,王航宇,邱志明.一种模糊ELECTRE多属性决 attribute decision making problems[J].Journal of Kun-

.50 智能系统学报 第5卷 ming University of Science and Technology:Science and CAAI Transactions on Intelligent Systems,2008,3(6): Technology,2008,33(6):113-116. 476486. [15]刘秀梅,赵克勤.基于联系数复运算的区间数多属性决 [21]BRYSON N,MOBOLURIN A.An action Leaming evalua- 策方法及应用[J].数学的实践与认识,2008,38 tion procedure for multiple criteria decision making prob- (23):5764 lems[J].European Journal of Operational Research, LIU Xiumei,ZHAO Keqin.Multiple attribute decision 1996,6:379-386. making and its applications based on complex number a- [22]卜广志,张字文.基于三参数区间数的灰色模糊综合评 rithmetic operation of connection number with interval num- 判[J].系统工程与电子技术,2001,23(9):4345, bers[J].Mathematics in Practice and Theory,2008,38 62. (23):5764. BU Guangzhi,ZHANG Yuwen.Grey fuzzy comprehensive [16]刘秀梅,赵克勤。基于区间数确定性与不确定性相互作 evaluation method based on interval numbers of three pa- 用点的多属性决策[J刀].数学的实践与认识,2009,39 rameters[J].Systems Engineering and Electronics,2001, (8):68-75. 23(9):4345,62. LIU Xiumei,ZHAO Keqin.Multiple attribute decision [23]王坚强.信息不完全的UZZY群体多准则决策的规划 making based on the interval numbers certainty and the un- 方法[J].系统工程与电子技术,2004,26(11):1604 certainty interact on each other[J].Mathematics in Prac- 1608. tice and Theory,2009,39(8):68-75. WANG Jianqiang.Programming method of fuzzy group [17]刘秀梅,赵克勒.基于SPA的D-U空间的区间数多属 multiple criteria decision making with incomplete informa- 性决策模型与应用[J].模糊系统与数学,2009,23 tion[J].Systems Engineering and Electronics,2004,26 (2):167-174. (11):1604-1608. LIU Xiumei,ZHAO Keqin.Multiple attribute decision [24]王恕,张亦飞,郝春玲,等.一种区间数多属性决策 making and its applications with interval numbers based on 新方法及其工程应用[J].水利水运工程学报,2006 D-U space of SPA[J].Fuzzy Systems and Mathematics (3):5458. 2009,23(2):167-174. WANG Shu,ZHANG Yifei,HAO Cunling,et al.A new [18]刘秀梅.基于联系数的三角模糊数多指标评价方法 method of multi-attribute decision-making for interval [J].淮阴工学院学报,2008,17(5):30-33. numbers and its engineering application[J].Hydro-Sci- LIU Xiumei.Multiple attribute decision making and its ap- ence and Engineering,2006(3):54-58. plications based on the connection number with triangular 作者简介: fuzzy numbers[J].Journal of Huaiyin Institute of Technol- 赵克勤,男,1950年生,研究员,浙 0w,2008,17(5):30-33. 江省诸暨市联系数学研究所所长,中国 [19]王梓坤.概率论基础及其应用[M].北京:科学出版 人工智能学会理事、人工智能基础专业 社,1979:218-219. 委员会副主任、集对分析联系数学专业 [20]赵克勤.二元联系数A+Bi的理论基础与基本算法及 筹备委员会主任.主要研究方向为联系 在人工智能中的应用[J].智能系统学报,2008,3 数学,1989年提出集对分析(联系数 (6):476-486 学),已出版《集对分析及其初步应用》专著1部,发表学术 ZHAO Kegin.The theoretical basis and basic algorithm of 论文90余篇, binary connectionA Bi and its application in AI[J]