
第4卷第2期 智能系统学报 Vol 4 Ng 2 2009年4月 CAA I Transactions on Intelligent Systems Apr 2009 基于自控测距法的机器人位姿估计 王晓宇1闫继宏2徐莉红3 (1航天东方红卫星有限公司,北京100094,2哈尔滨工业大学机器人研究所,黑龙江哈尔滨150080,3304厂科研2所, 山西长治046012) 摘要:针对两轮自平衡机器人运行过程中遇到打滑、越障、碰撞等异常事件,测程法进行位姿估计失效的情况,提 出一种自控测距法.结合改进的Gy rodometry方法,通过融合码盘、陀螺仪与加速度计数据对机器人的位姿进行估计, 实现了机器人的准确定位,解决了非系统定位误差对机器人位姿估计的影响,降低了陀螺仪、加速度计固有漂移的 不利影响,提高了两轮自平衡机器人的定位精度.实验结果显示与测程法误差相比自控测距法位置误差降为13,方 向误差降为16,验证了自控测距法的有效性。 关键词:位姿估计;自控测距法;Gyrodometry法 中图分类号:TP242文献标识码:A文章编号:1673-4785(2009)02016906 mprovng estmations of a robot's position and a ttitude with accelerometer enhanced odometry WANG Xiao-yu',YAN Ji-hong,XU L i-hong (1.DFH Satellite Company Ltd,Beijing 100094,China;2 Robotics Institute,Harbin Institute of Technobgy,Harbin 150080, China;3 Number 2 Scientific Research Institute,Number 304 Facbry,Changzhi046012,China) Abstract:Unpredictable events can occur in the navigational processes of wowheeled self-balanc ing robots,such as wheel-slippage,interaction with obstacles,and bumps These invalidate position and attitude estmates There- fore,an mproved method was developed for accurate positioning of robots The accodometry method adds acceler- ometer data to the mp roved Gyrodometry method,fusing encoder data with inertial sensor data Thismethod elmi nates the effect of non-systematic errors on robot position and attitude estmation and reduces ill-effects due to inher ent drift of the gyro and accelerometer As a result,positional accuracy is greatly mproved Expermental results showed that positional errors decrease by one-third and orientation errors decline by one-sixth,verifying the effec- tiveness of the accodometry method Keywords:position and attitude estmation;accodometry method:Gyrodometry method 机器人定位是导航的一个重要的研究方向,要求外部传感器的信息就能实现对机器人位置的估计」 机器人能够在运动过程中精确的感知自身在环境中测程法具有良好的短期精度、实现简单、成本低、采 的位置和姿态.移动机器人通常采用2种基本的定位 样速率高、实时性好的优点,但是存在误差无界的累 方法:绝对定位法和相对定位法,大多数方法采用绝 积增长.因此需要采用路标、光电探测器和超声传感 对定位与相对定位相结合来进行位姿估计到 器等绝对定位系统进行外部测量,对测程法产生的 测程法根据路程随时间累积而增加的原理,通 累积误差进行修正以提高机器人的定位精度.安装 过控制车轮旋转和车轮转向角的光电码盘获得机器 绝对定位系统将增加成本:因此需要提高测程法与 人的当前位置与初始位置的偏差,然后计算机器人 传感器精度,减少使用绝对定位系统的密度和修正 本体与车轮、转向之间的关系得到位置信息,不需要 的次数,提高系统响应的实时性,降低成本提高定位 精度4) 收稿日期:200805-14 密歇根大学的Borenstein等I提出了UMBmark 基金项目:“863国家高技术研究发展计划资助项目(20064404245)】 通信作者:王晓字.Email wxyhitl97745@yahoo com cn (University ofM ichigan benchmark test)方法,针对测 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 4卷第 2期 智 能 系 统 学 报 Vol. 4 №. 2 2009年 4月 CAA I Transactions on Intelligent System s Ap r. 2009 基于自控测距法的机器人位姿估计 王晓宇 1 ,闫继宏 2 ,徐莉红 3 (1. 航天东方红卫星有限公司 ,北京 100094; 2. 哈尔滨工业大学 机器人研究所 ,黑龙江 哈尔滨 150080; 3. 304厂科研 2所 , 山西 长治 046012) 摘 要 :针对两轮自平衡机器人运行过程中遇到打滑、越障、碰撞等异常事件 ,测程法进行位姿估计失效的情况 ,提 出一种自控测距法. 结合改进的 Gyrodometry方法 ,通过融合码盘、陀螺仪与加速度计数据对机器人的位姿进行估计 , 实现了机器人的准确定位 ,解决了非系统定位误差对机器人位姿估计的影响 ,降低了陀螺仪、加速度计固有漂移的 不利影响 ,提高了两轮自平衡机器人的定位精度. 实验结果显示与测程法误差相比自控测距法位置误差降为 1 /3,方 向误差降为 1 /6,验证了自控测距法的有效性. 关键词 :位姿估计 ;自控测距法 ; Gyrodometry法 中图分类号 : TP242 文献标识码 : A 文章编号 : 167324785 (2009) 0220169206 Improving estimations of a robot’ s position and attitude with accelerometer enhanced odometry WANG Xiao2yu 1 , YAN Ji2hong 2 , XU L i2hong 3 (1. DFH Satellite Company Ltd. , Beijing 100094, China; 2. Robotics Institute, Harbin Institute of Technology, Harbin 150080, China; 3. Number 2 Scientific Research Institute, Number 304 Factory, Changzhi 046012, China) Abstract:Unp redictable events can occur in the navigational p rocesses of two2wheeled self2balancing robots, such as wheel2slippage, interaction with obstacles, and bump s. These invalidate position and attitude estimates. There2 fore, an imp roved method was developed for accurate positioning of robots. The accodometry method adds acceler2 ometer data to the imp roved Gyrodometry method, fusing encoder data with inertial sensor data. Thismethod elim i2 nates the effect of non2systematic errors on robot position and attitude estimation and reduces ill2effects due to inher2 ent drift of the gyro and accelerometer. A s a result, positional accuracy is greatly imp roved. Experimental results showed that positional errors decrease by one2third and orientation errors decline by one2sixth, verifying the effec2 tiveness of the accodometry method. Keywords: position and attitude estimation; accodometry method; Gyrodometry method 收稿日期 : 2008205214. 基金项目 :“863”国家高技术研究发展计划资助项目 (2006AA04Z245). 通信作者 :王晓宇. E2mail: wxyhit197745@yahoo. com. cn. 机器人定位是导航的一个重要的研究方向 ,要求 机器人能够在运动过程中精确的感知自身在环境中 的位置和姿态. 移动机器人通常采用 2种基本的定位 方法:绝对定位法和相对定位法 ,大多数方法采用绝 对定位与相对定位相结合来进行位姿估计 [ 123 ] . 测程法根据路程随时间累积而增加的原理 ,通 过控制车轮旋转和车轮转向角的光电码盘获得机器 人的当前位置与初始位置的偏差 ,然后计算机器人 本体与车轮、转向之间的关系得到位置信息 ,不需要 外部传感器的信息就能实现对机器人位置的估计. 测程法具有良好的短期精度、实现简单、成本低、采 样速率高、实时性好的优点 ,但是存在误差无界的累 积增长. 因此需要采用路标、光电探测器和超声传感 器等绝对定位系统进行外部测量 ,对测程法产生的 累积误差进行修正以提高机器人的定位精度. 安装 绝对定位系统将增加成本 ;因此需要提高测程法与 传感器精度 ,减少使用绝对定位系统的密度和修正 的次数 ,提高系统响应的实时性 ,降低成本提高定位 精度 [ 427 ] . 密歇根大学的 Borenstein等 [ 8 ]提出了 UMBmark (University ofM ichigan benchmark test)方法 ,针对测

·170 智能系统学报 第4卷 程法系统误差进行测量和修正,并用实验验证了该 选用相对定位传感器加速度计、陀螺仪、码盘实时测 方法能够使定位精度至少提高一个数量级.华中科 量机器人姿态采用码盘、加速度计实时测量机器人 技大学的王卫华等2针对UMBmark提出了改进的 位置,并定期通过绝对定位传感器超声传感器组、光 算法,进一步提高了测程法的定位精度.对于非系统 电探测器组和路标系统对实时位姿信息进行修正, 误差中的转向问题,Borenstein等II提出了Gy 定位用传感器组成如图1所示 odometry方法,几乎完全消除了陀螺仪漂移误差的 偏航轴陀螺仅时储航姿偏航轴姿态 同期修正 超声传感器饥 影响,有效地解决了异常情况下的转向估计问题,提 码盘 周期修正 超市传感器 高了测程法精度.还针对测程法中的非系统误差车 实时平面位置 平面位置 加速度计 红外传感器 轮打滑提出改进的测程法,进一步提高定位精 周期修正 度【o1 俯仰轴陀螺仪送时俯仰姿泰俯仰轴姿态 红外传感器织 当前机器人异常情况下定位问题的研究主要针 图1传感器配置示意图 对多轮机器人,研究方向主要集中在转向(偏航轴) Fig 1 Schematic diagram of sensors 方面,解决问题时只考虑方向信息而未考虑异常情 3 自控测距法 况时的位置估计问题,对于两轮机器人异常情况下 的定位研究还未开展.针对两轮机器人运行过程中 为解决异常情况下非系统误差问题,对机器人 可能遇到的打滑越障、碰撞等异常情况造成不可预 车轮与地面的相互作用进行了研究,提出一种融合 测的定位误差,位姿估计失效、机器人任务失败时, 码盘数据与加速度计数据的方法进行位置估计: 提出一种直接、有效的自控测距法(accelerometer- 31异常过程分析 odometry),结合改进的Gy rodometry方法发现并修 当两轮自平衡机器人进行直线运动,左轮越过 正非系统的定位误差,提高定位精度 一个障碍物时,要想保持机器人继续进行直线运动 左轮就要多走一段距离△D公D与车轮直径和障碍 1测程法误差分析 物的高度有关人.当码盘没有“意识到碰到障碍物 测程法的前提假设是车轮旋转可以转换成相对 时,机器人的2个车轮将尽量保持相同的转速前进, 地面的线位移,此假设只在有限范围内有效,在极端 左轮将比右轮少移动△D距离,造成机器人向有障 情况下比如车轮打滑会造成较大的误差.除了完全 碍物一侧偏移,运动轨迹也从直线变成曲线.越障结 打滑这种极端情况以外还有几种造成码盘读数不能 束后机器人将继续保持直线运动,但是却产生了方 正确转换成位移的因素.这些误差源可以分成系统 向误差和位置误差,如图2所示.越障前机器人车轴 误差和非系统误差2类: 方位如线L,所示,越障后车轴方位如线L2所示,L3 1)系统误差:机器人结构误差、车轮直径不相 为没有障碍时机器人的方位,L:为机器人瞬时俯仰 等、车轮实际直径的平均值与标称值不一致、车轮偏 轴姿态,F方向为辅助计算方向 心、有效轮距不确定、码盘分辨率、采样率限制 2)非系统误差:车轮打滑、地面不平、越障、碰 0 撞、干扰、惯性传感器漂移误差 F方向 系统误差主要由运动学模型不完善造成,非系 1A 统误差主要由外部环境影响造成.在平坦的室内环 境中,系统误差对定位误差的影响超过了非系统误 差;在地面不规则的环境中,非系统误差是定位误差 0 的主要误差源.非系统误差是不可预期的,它们会导 致产生大的位置误差 2位姿估计用传感器 图2测程法误差示意图 Fig 2 Schematic diagram of odometry eror 机器人位姿估计采用绝对定位与相对定位相结 合的方法,通过分析常用位姿测量传感器的特点,综 机器人越障过程位姿变化非常复杂,需要采用 合考虑机器人控制的实际情况和经济性因素,最终 绝对定位传感器的测量值,再结合机器人的瞬时姿 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
程法系统误差进行测量和修正 ,并用实验验证了该 方法能够使定位精度至少提高一个数量级. 华中科 技大学的王卫华等 [ 2 ]针对 UMBmark提出了改进的 算法 ,进一步提高了测程法的定位精度. 对于非系统 误差 中的转 向问题 , Borenstein 等 [ 9 ] 提 出 了 Gy2 rodometry方法 ,几乎完全消除了陀螺仪漂移误差的 影响 ,有效地解决了异常情况下的转向估计问题 ,提 高了测程法精度. 还针对测程法中的非系统误差车 轮打滑提出改进的测程法 , 进一步提高定位精 度 [ 10 ] . 当前机器人异常情况下定位问题的研究主要针 对多轮机器人 ,研究方向主要集中在转向 (偏航轴 ) 方面 ,解决问题时只考虑方向信息而未考虑异常情 况时的位置估计问题 ,对于两轮机器人异常情况下 的定位研究还未开展. 针对两轮机器人运行过程中 可能遇到的打滑、越障、碰撞等异常情况造成不可预 测的定位误差 ,位姿估计失效、机器人任务失败时 , 提出一种直接、有效的自控测距法 ( accelerometer2 odometry) ,结合改进的 Gyrodometry方法发现并修 正非系统的定位误差 ,提高定位精度. 1 测程法误差分析 测程法的前提假设是车轮旋转可以转换成相对 地面的线位移 ,此假设只在有限范围内有效 ,在极端 情况下比如车轮打滑会造成较大的误差. 除了完全 打滑这种极端情况以外还有几种造成码盘读数不能 正确转换成位移的因素. 这些误差源可以分成系统 误差和非系统误差 2类 : 1) 系统误差 :机器人结构误差、车轮直径不相 等、车轮实际直径的平均值与标称值不一致、车轮偏 心、有效轮距不确定、码盘分辨率、采样率限制. 2) 非系统误差 :车轮打滑、地面不平、越障、碰 撞、干扰、惯性传感器漂移误差. 系统误差主要由运动学模型不完善造成 ,非系 统误差主要由外部环境影响造成. 在平坦的室内环 境中 ,系统误差对定位误差的影响超过了非系统误 差 ;在地面不规则的环境中 ,非系统误差是定位误差 的主要误差源. 非系统误差是不可预期的 ,它们会导 致产生大的位置误差. 2 位姿估计用传感器 机器人位姿估计采用绝对定位与相对定位相结 合的方法 ,通过分析常用位姿测量传感器的特点 ,综 合考虑机器人控制的实际情况和经济性因素 ,最终 选用相对定位传感器加速度计、陀螺仪、码盘实时测 量机器人姿态 ,采用码盘、加速度计实时测量机器人 位置 ,并定期通过绝对定位传感器超声传感器组、光 电探测器组和路标系统对实时位姿信息进行修正. 定位用传感器组成如图 1所示. 图 1 传感器配置示意图 Fig. 1 Schematic diagram of sensors 3 自控测距法 为解决异常情况下非系统误差问题 ,对机器人 车轮与地面的相互作用进行了研究 ,提出一种融合 码盘数据与加速度计数据的方法进行位置估计. 3. 1 异常过程分析 当两轮自平衡机器人进行直线运动 ,左轮越过 一个障碍物时 ,要想保持机器人继续进行直线运动 左轮就要多走一段距离 ΔD (ΔD 与车轮直径和障碍 物的高度有关 ). 当码盘没有“意识到 ”碰到障碍物 时 ,机器人的 2个车轮将尽量保持相同的转速前进 , 左轮将比右轮少移动 ΔD 距离 ,造成机器人向有障 碍物一侧偏移 ,运动轨迹也从直线变成曲线. 越障结 束后机器人将继续保持直线运动 ,但是却产生了方 向误差和位置误差 ,如图 2所示. 越障前机器人车轴 方位如线 L1 所示 ,越障后车轴方位如线 L2 所示 , L3 为没有障碍时机器人的方位 , L4 为机器人瞬时俯仰 轴姿态 , F方向为辅助计算方向. 图 2 测程法误差示意图 Fig. 2 Schematic diagram of odometry error 机器人越障过程位姿变化非常复杂 ,需要采用 绝对定位传感器的测量值 ,再结合机器人的瞬时姿 ·170· 智 能 系 统 学 报 第 4卷

第2期 王晓宇,等:基于自控测距法的机器人位姿估计 ·171 态值,才能得到越障过程中机器人的位姿信息.其 前进方向的位移x由测量机器人位置的超声传感器 中:方向角δ由测量偏航轴姿态的超声传感器组测 的测量值、测量机器人位置的光电探测器的测量值 量值计算后得到:俯仰轴姿态角0由测量俯仰轴姿 方向误差和俯仰轴姿态共同确定.通过上述分析,可 态的光电探测器组测量值计算后得到:横向位移 以得到机器人越障过程中的位姿方程: Lped (1)-Lpedz(1 0()arctan Dped 8(=arctan- Lus (0-Lus (1 (1) Dus cos0(t) x(W=fLm(d+D Jcos0(tcos△δ(l-Dus sin0(dcos△δ(d: z()=fLa()+D Jcos0()sin△δ()-Dsin0()sin△8(. 式中:Lp,山p,分别为测量俯仰轴姿态的光电探测 感器测得的距离,D、D分别为测量位置的超声 器1、2测得的距离,Dp为测量俯仰轴姿态的2个光 传感器与机器人中心、机器人底盘之间的距离」 电探测器之间的距离,L,、L,分别为测量方向角的 根据图2和式(1),可以得到机器人越障过程 超声传感器1、2测得的距离,D为测量方向角的2 中的位姿误差方程: 个超声传感器之间的距离,L为测量位置的超声传 △0(w=acan剑f):Ld Dped △8()=arctan Lus (1-Lus (1 Duscos0(v (2) △x()='()t-L,()+D Jcos0()cos△6()-Du Sin0()cos△8(W; △z()=fLa()+D.Jcos0(dsin△8()-Ds sin0(ysin△6()-(L+Dm. 式中:△0为机器人俯仰轴姿态角,△8为方向误差, 缆作为障碍物.单个障碍物对机器人位置的影响如 △x为X方向的位置误差,△为Z方向的位置误差, 图3所示,在越障过程中加速度计只在越障时启动, V为机器人前进速度,L为测量位置的超声传感器 越障结束后停止,尽管其自身存在位置误差累积,但 测得的机器人与路标的初始距离」 是由于工作时间很短,因此位置误差累积可以忽略 由于机器人越障时间很短,越障过程中Z方向 由图可见,加速度计测量的位置较测程法测量的位 的位置变化较小,与机器人正常运行时由于方向偏 置更接近于真实位置 差导致的位置误差相比很小,而X方向的位置变化 29*10 较大:因此不研究Z方向的位置估计问题,只研究X 实际位置曲线 2.48 --.测程法位誉曲线 方向的位置估计问题 2.47 加速度计位置曲线 在机器人越障过程中值得注意的问题是,机器 2.46 人越障时先向障碍物一侧运动,然后再向远离障碍 2.45 物方向运动.因为机器人遇到障碍时左轮上坡,此时 2.44 左轮动能转化为势能,机器人左轮速度变慢,机器人 2.43引 向左侧偏移:到达障碍物最高点后下坡,左轮势能转 2.42 化为动能,机器人左轮速度变快,机器人向右侧偏 24.4 24.524.624.724.824.9 移.由于码盘“意识到"左轮转速的变化,因此对右 时间/ 轮转速提供对应于左轮转速的修正信息:但是码盘 图3越过单个障碍时各传感器位置估计曲线 并没有“意识到此时左轮产生了距离误差△D,因 Fig 3 The position curves of the single obstacle negotiation 此机器人没有完全回到原来的方向,而是产生了方 向偏移△δ和距离偏移△D 测程法根据车轮运行路程进行位置估计,越障 机器人以01m/s的速度在光滑路面运行,运 过程中车轮运行路程大于真实距离,码盘认为己经 行距离为3m,采样周期10ms选择间隔05m的电 到达指定位置,但事实上并没到达;因此测程法的误 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
态值 ,才能得到越障过程中机器人的位姿信息. 其 中 :方向角 δ由测量偏航轴姿态的超声传感器组测 量值计算后得到;俯仰轴姿态角 θ由测量俯仰轴姿 态的光电探测器组测量值计算后得到;横向位移 z、 前进方向的位移 x由测量机器人位置的超声传感器 的测量值、测量机器人位置的光电探测器的测量值、 方向误差和俯仰轴姿态共同确定. 通过上述分析 ,可 以得到机器人越障过程中的位姿方程 : θ( t) = a rctan Lped1 ( t) - Lped2 ( t) Dped ; δ( t) = a rctan Lus1 ( t) - Lus2 ( t) Dus co sθ( t) ; x ( t) = [Lus ( t) + Dus1 ] cosθ( t) cosΔδ( t) - Dus2 sinθ( t) co sΔδ( t) ; z( t) = [Lus ( t) + Dus1 ] co sθ( t) sinΔδ( t) - Dus2 sinθ( t) sinΔδ( t). (1) 式中 : Lped1、Lped2分别为测量俯仰轴姿态的光电探测 器 1、2测得的距离 , Dped为测量俯仰轴姿态的 2个光 电探测器之间的距离 , Lus1、Lus2分别为测量方向角的 超声传感器 1、2测得的距离 , Dus为测量方向角的 2 个超声传感器之间的距离 , Lus为测量位置的超声传 感器测得的距离 , Dus1、Dus2分别为测量位置的超声 传感器与机器人中心、机器人底盘之间的距离. 根据图 2和式 ( 1) ,可以得到机器人越障过程 中的位姿误差方程 : Δθ( t) = a rctan Lped1 ( t) - Lped2 ( t) Dped ; Δδ( t) = a rctan Lus1 ( t) - Lus2 ( t) Dus cosθ( t) ; Δx ( t) = V ( t) t - [Lus ( t) + Dus1 ] co sθ( t) cosΔδ( t) - Dus2 sinθ( t) cosΔδ( t) ; Δz( t) = [Lus ( t) + Dus1 ] cosθ( t) sinΔδ( t) - Dus2 sinθ( t) sinΔδ( t) - (Lus0 + Dus1 ). (2) 式中 :Δθ为机器人俯仰轴姿态角 ,Δδ为方向误差 , Δx为 X方向的位置误差 ,Δz为 Z方向的位置误差 , V为机器人前进速度 , Lus0为测量位置的超声传感器 测得的机器人与路标的初始距离. 由于机器人越障时间很短 ,越障过程中 Z方向 的位置变化较小 ,与机器人正常运行时由于方向偏 差导致的位置误差相比很小 ,而 X 方向的位置变化 较大;因此不研究 Z方向的位置估计问题 ,只研究 X 方向的位置估计问题. 在机器人越障过程中值得注意的问题是 ,机器 人越障时先向障碍物一侧运动 ,然后再向远离障碍 物方向运动. 因为机器人遇到障碍时左轮上坡 ,此时 左轮动能转化为势能 ,机器人左轮速度变慢 ,机器人 向左侧偏移;到达障碍物最高点后下坡 ,左轮势能转 化为动能 ,机器人左轮速度变快 , 机器人向右侧偏 移. 由于码盘“意识到 ”左轮转速的变化 ,因此对右 轮转速提供对应于左轮转速的修正信息;但是码盘 并没有“意识到 ”此时左轮产生了距离误差 ΔD,因 此机器人没有完全回到原来的方向 ,而是产生了方 向偏移 Δδ和距离偏移 ΔD. 机器人以 0. 1 m /s的速度在光滑路面运行 ,运 行距离为 3m,采样周期 10m s,选择间隔 0. 5m的电 缆作为障碍物. 单个障碍物对机器人位置的影响如 图 3所示 ,在越障过程中加速度计只在越障时启动 , 越障结束后停止 ,尽管其自身存在位置误差累积 ,但 是由于工作时间很短 ,因此位置误差累积可以忽略. 由图可见 ,加速度计测量的位置较测程法测量的位 置更接近于真实位置. 图 3 越过单个障碍时各传感器位置估计曲线 Fig. 3 The position curves of the single obstacle negotiation 测程法根据车轮运行路程进行位置估计 ,越障 过程中车轮运行路程大于真实距离 ,码盘认为已经 到达指定位置 ,但事实上并没到达;因此测程法的误 第 2期 王晓宇 ,等 :基于自控测距法的机器人位姿估计 ·171·

·172· 智能系统学报 第4卷 差较大,不应再完全信任测程法数据.加速度计测量 用测程法数据,减小了由于使用加速度计而产生的 数据波动较大,由于存在漂移误差导致加速度计产 漂移误差,加速度计起作用的时刻往往是测程法误 生位置误差,但其测得的位置数据短期精度高,可以 差最大的时刻」 与测程法数据融合共同使用测量位置信息.单独的 4直线越障实验 一次碰撞对机器人传感器位姿的影响如图4所示. 测程法位置误差变化曲线 6 为验证自控测距法结合改进的Gyrodometry方 一加速度计位省误差变化曲线 ··加速度计与测程法位置误差变化曲线 法处理机器人越障等异常情况时的性能,将其应用 4 于两轮自平衡机器人系统.系统误差采用UMBmark 2 方法处理,非系统误差中的转向误差采用改进的 Gyrodometry方法处理,非系统误差中的位置误差采 用自控测距法处理 41实验系统 23.023.524.024.525.025.526.0 两轮自平衡机器人系统由机器人本体控制器、 时间/s 驱动器、电池、光电码盘、传感与检测系统和车轮组 图4越过单个障碍时各传感器位置误差变化曲线 成机器人采用两轮同轴、分别独立驱动的方式.机 Fig 4 The position eror change curves of the single obsta- 器人HBot高Q24m,重20kg两轮距离02m, cle negotiation 轮半径007m,结构如图5所示 32自控测距法的具体实现 针对机器人处于异常情况时,各传感器的误差 电池组 控制电路 特性,提出一种融合加速度计与测程法数据的自控 测距算法.测程法存在的最严重的问题就是系统遭 传感器 遇异常情况时,会出现非系统误差.机器人不能通过 驱动器 标定来补偿非系统误差,也无法预测这些误差.加速 码盘 度计存在的主要问题是固有的漂移误差,将导致位 电机 置误差无界增长.而自控测距法能够降低上述问题 图5两轮自平衡机器人HBot 的不利影响 Fig 5 Two-wheeled self-balanced robot-H IIBot 自控测距法是根据测量得到的测程法位置估计 曲线与加速度计位置估计曲线仅在短时间不重合的 42实验过程 假设提出的,实验数据如图3所示 机器人沿连续的直墙进行直线越障实验,根据 图4中虚线是测程法位置误差变化曲线,用 机器人的实际尺寸、越障能力及实验平台,选择电缆 △D表示;实线表示加速度计位置误差变化曲线, 作为障碍物,障碍物的数量及尺寸如表1所示,路标 用△D表示;点划线表示测程法位置变化与加速度 及障碍物布置如图6所示」 计位置变化之差,用△Dm=△D-△D表示.自控 表1障碍物的数量及尺寸 测距法就是将△D,与预先设置的阀值△Dh进行比 Table 1 Num ber and dimension of obstacles 较,如果有 障碍物 123456 |△D。|>△Dhes, (3) 直径mm224466 机器人瞬时位置估计信任加速度计数据,位置值根 使用路标对位置信息进行周期性修正,以消除 据加速度计位置增量△D计算得到.如果有: 惯性传感器无界的累积误差影响.每隔Q5m设置 |△Dm|<△Dhes 4) 2个路标,障碍物距离路标005m在奇数路标处启 机器人瞬时位置估计信任测程法数据,位置值根据 动加速度计、陀螺仪开始提供位姿信息,其初值由自 测程法位置增量△D计算得到, 控测距法、改进的Gy rodom etry方法计算得到的位姿 从越障的整体过程分析,加速度计信息只在越 终值确定:运行Q1m后遇到偶数路标停止加速度 障过程中很少的采样间隔中起作用,其余时刻都采 @1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
差较大 ,不应再完全信任测程法数据. 加速度计测量 数据波动较大 ,由于存在漂移误差导致加速度计产 生位置误差 ,但其测得的位置数据短期精度高 ,可以 与测程法数据融合共同使用测量位置信息. 单独的 一次碰撞对机器人传感器位姿的影响如图 4所示. 图 4 越过单个障碍时各传感器位置误差变化曲线 Fig. 4 The position error change curves of the single obsta2 cle negotiation 3. 2 自控测距法的具体实现 针对机器人处于异常情况时 ,各传感器的误差 特性 ,提出一种融合加速度计与测程法数据的自控 测距算法. 测程法存在的最严重的问题就是系统遭 遇异常情况时 ,会出现非系统误差. 机器人不能通过 标定来补偿非系统误差 ,也无法预测这些误差. 加速 度计存在的主要问题是固有的漂移误差 ,将导致位 置误差无界增长. 而自控测距法能够降低上述问题 的不利影响. 自控测距法是根据测量得到的测程法位置估计 曲线与加速度计位置估计曲线仅在短时间不重合的 假设提出的 ,实验数据如图 3所示. 图 4中虚线是测程法位置误差变化曲线 , 用 ΔDodo表示;实线表示加速度计位置误差变化曲线 , 用 ΔDacc表示;点划线表示测程法位置变化与加速度 计位置变化之差 ,用 ΔDao =ΔDodo -ΔDacc表示. 自控 测距法就是将ΔDao与预先设置的阀值ΔDthres进行比 较 ,如果有 | ΔDao | >ΔDthres , (3) 机器人瞬时位置估计信任加速度计数据 ,位置值根 据加速度计位置增量 ΔDacc计算得到. 如果有 : | ΔDao | <ΔDthres , (4) 机器人瞬时位置估计信任测程法数据 ,位置值根据 测程法位置增量 ΔDodo计算得到. 从越障的整体过程分析 ,加速度计信息只在越 障过程中很少的采样间隔中起作用 ,其余时刻都采 用测程法数据 ,减小了由于使用加速度计而产生的 漂移误差 ,加速度计起作用的时刻往往是测程法误 差最大的时刻. 4 直线越障实验 为验证自控测距法结合改进的 Gyrodometry方 法处理机器人越障等异常情况时的性能 ,将其应用 于两轮自平衡机器人系统. 系统误差采用 UMBmark 方法处理 , 非系统误差中的转向误差采用改进的 Gyrodometry方法处理 ,非系统误差中的位置误差采 用自控测距法处理. 4. 1 实验系统 两轮自平衡机器人系统由机器人本体、控制器、 驱动器、电池、光电码盘、传感与检测系统和车轮组 成. 机器人采用两轮同轴、分别独立驱动的方式. 机 器人 H ITBot高 0. 24 m,重 2. 0 kg,两轮距离 0. 2 m, 轮半径 0. 07 m,结构如图 5所示. 图 5 两轮自平衡机器人 H ITBot Fig. 5 Two2wheeled self2balanced robot2H ITBot 4. 2 实验过程 机器人沿连续的直墙进行直线越障实验 ,根据 机器人的实际尺寸、越障能力及实验平台 ,选择电缆 作为障碍物 ,障碍物的数量及尺寸如表 1所示 ,路标 及障碍物布置如图 6所示. 表 1 障碍物的数量及尺寸 Table 1 Num ber and d im en sion of obstacles 障碍物 1 2 3 4 5 6 直径 /mm 2 2 4 4 6 6 使用路标对位置信息进行周期性修正 ,以消除 惯性传感器无界的累积误差影响. 每隔 0. 5 m设置 2个路标 ,障碍物距离路标 0. 05 m. 在奇数路标处启 动加速度计、陀螺仪开始提供位姿信息 ,其初值由自 控测距法、改进的 Gyrodometry方法计算得到的位姿 终值确定;运行 0. 1 m后遇到偶数路标停止加速度 ·172· 智 能 系 统 学 报 第 4卷
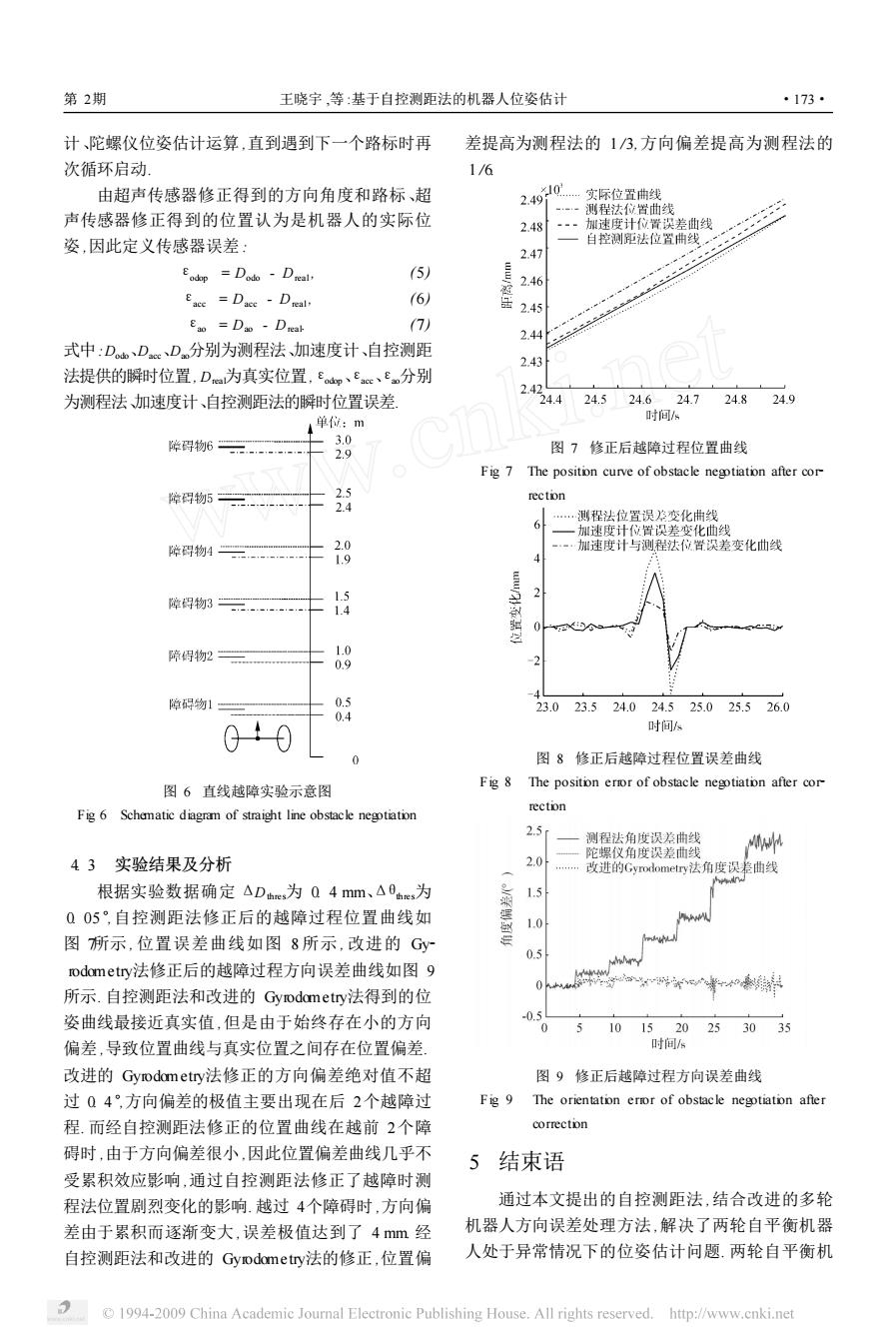
第2期 王晓宇,等:基于自控测距法的机器人位姿估计 ·173 计、陀螺仪位姿估计运算,直到遇到下一个路标时再 差提高为测程法的13,方向偏差提高为测程法的 次循环启动 1/6 由超声传感器修正得到的方向角度和路标、超 0…实际位置曲线 2.491 声传感器修正得到的位置认为是机器人的实际位 --测程法位置曲线 2.48 加速度计位置误差曲线 姿,因此定义传感器误差: 自控测法位置曲线 2.47 Eodop =Dodo-D neal. (5) 2.46 Eace =Dace Dteal. 16) 2.45 E3 =Dao-Ditak (7) 2.44 式中:D、DcD分别为测程法加速度计、自控测距 2.43 法提供的瞬时位置,D=为真实位置,£op、eacc、£n分别 2.4 为测程法加速度计、自控测距法的瞬时位置误差 24.424.524.624.7 24.824.9 4单位:m 时间/s 降碍物6= 3.0 2.9 图7修正后越障过程位置曲线 Fig 7 The positon curve of obstacle negtiation after cor 得物5 2.5 ------ rection 2.4 6 …测程法位置误差变化曲线 一加速度计位置误差变化曲线 碎碍物A 2.0 -加速度计与测程法位置误差变化曲线 19 障得物3 5 1.4 0<5s 疏得物2 1.0 0.9 障碍物1 0.5 0.4 23.023.524.024.525.025.526.0 00 时间 图8修正后越障过程位置误差曲线 图6直线越障实验示意图 Fig 8 The position eror of obstacle negotiation after cor rection Fig 6 Schematic diagram of straight line obstacle negotiation 2.5r 测程法角度误差曲线 M 陀螺仪角度误差曲线 43实验结果及分析 2.0 改进的Gyrodometry法角度误差曲线 根据实验数据确定△Dhe为Q4mm、△0hes为 1.5 Q05°,自控测距法修正后的越障过程位置曲线如 1.0 图所示,位置误差曲线如图8所示,改进的Gy 0.5 rodometry法修正后的越障过程方向误差曲线如图9 所示.自控测距法和改进的Gy rodometry法得到的位 姿曲线最接近真实值,但是由于始终存在小的方向 05 0 5 101520253035 偏差,导致位置曲线与真实位置之间存在位置偏差。 时间/s 改进的Gyrodom etry法修正的方向偏差绝对值不超 图9修正后越障过程方向误差曲线 过04°,方向偏差的极值主要出现在后2个越障过 Fig 9 The orientation eror of obstacle negotiation after 程.而经自控测距法修正的位置曲线在越前2个障 correction 碍时,由于方向偏差很小,因此位置偏差曲线几乎不 5结束语 受累积效应影响,通过自控测距法修正了越障时测 程法位置剧烈变化的影响.越过4个障碍时,方向偏 通过本文提出的自控测距法,结合改进的多轮 差由于累积而逐渐变大,误差极值达到了4mm经 机器人方向误差处理方法,解决了两轮自平衡机器 自控测距法和改进的Gyodome try法的修正,位置偏 人处于异常情况下的位姿估计问题.两轮自平衡机 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.net
计、陀螺仪位姿估计运算 ,直到遇到下一个路标时再 次循环启动. 由超声传感器修正得到的方向角度和路标、超 声传感器修正得到的位置认为是机器人的实际位 姿 ,因此定义传感器误差 : εodop = Dodo - Dreal , (5) εacc = Dacc - Dreal , (6) εao = Dao - Dreal . (7) 式中:Dodo、Dacc、Dao分别为测程法、加速度计、自控测距 法提供的瞬时位置, Dreal为真实位置,εodop、εacc、εao分别 为测程法、加速度计、自控测距法的瞬时位置误差. 图 6 直线越障实验示意图 Fig. 6 Schematic diagram of straight line obstacle negotiation 4. 3 实验结果及分析 根据实验数据确定 ΔDthres为 0. 4 mm、Δθthres为 0. 05°,自控测距法修正后的越障过程位置曲线如 图 7所示 , 位置误差曲线如图 8 所示 , 改进的 Gy2 rodometry法修正后的越障过程方向误差曲线如图 9 所示. 自控测距法和改进的 Gyrodometry法得到的位 姿曲线最接近真实值 ,但是由于始终存在小的方向 偏差 ,导致位置曲线与真实位置之间存在位置偏差. 改进的 Gyrodometry法修正的方向偏差绝对值不超 过 0. 4°,方向偏差的极值主要出现在后 2个越障过 程. 而经自控测距法修正的位置曲线在越前 2个障 碍时 ,由于方向偏差很小 ,因此位置偏差曲线几乎不 受累积效应影响 ,通过自控测距法修正了越障时测 程法位置剧烈变化的影响. 越过 4个障碍时 ,方向偏 差由于累积而逐渐变大 ,误差极值达到了 4 mm. 经 自控测距法和改进的 Gyrodometry法的修正 ,位置偏 差提高为测程法的 1 /3,方向偏差提高为测程法的 1 /6. 图 7 修正后越障过程位置曲线 Fig. 7 The position curve of obstacle negotiation after cor2 rection 图 8 修正后越障过程位置误差曲线 Fig. 8 The position error of obstacle negotiation after cor2 rection 图 9 修正后越障过程方向误差曲线 Fig. 9 The orientation error of obstacle negotiation after correction 5 结束语 通过本文提出的自控测距法 ,结合改进的多轮 机器人方向误差处理方法 ,解决了两轮自平衡机器 人处于异常情况下的位姿估计问题. 两轮自平衡机 第 2期 王晓宇 ,等 :基于自控测距法的机器人位姿估计 ·173·

·174· 智能系统学报 第4卷 器人直线越障实验结果验证了该方法能有效地提高 squares technique:theory and expermental validation [J]. 机器人的定位精度,降低定位误差.现阶段仅通过两 IEEE Transactions on Robotics,2005,21(5):994-1004. 轮自平衡机器人的直线越障实验对自控测距法进行 [8 ]BORENSTEN J,FENG L UMBmark:a benchmark test 验证,下一步还将研究机器人进行平面自由运动坡 for measuring odometry erors in mobile robots [C]//1995 面运动等复杂运动情况下自控测距法的有效性」 SPIE Conference on Mobile Robots Philadelphia,USA. 1995:305-311. 参考文献: [9 ]BORENSTEN J,FENGL Gyrodometry:a new method or combining data fiom gyros and odometry in mobile robots [1正卫华,熊有伦,孙容磊.测程法系统误差的测量与校 [C]//Proceedings of the 1996 IEEE Interational Confer 核[J]机器人,2004,26(5):454-460 ence on Robotics and Automation Minneapolis,MN,USA, WANGWeihua,XDNG Youlun,SN Ronglei Measure- 1996:423-428 ment and calibration of systematic erors of odometry J]. [10 ]BORENSTEN J,FENGL.Measurement and correction of Robot.2004.26(5):454-460 systematic odometry erors in mobile robots [J ]IEEE [2 ]L I Yan,GAO Feng.L N Tingqi,et al Study on multi-sen- Transactions on Robotics and Automation.1996,12 (6): sor data fusion for the wheeled mobile robot [C]//Proceed- 869-880 ings of the 5th World Congress on Intelligent Control and 作者简介: Automation Hangzhou,China,2004:4623-4626 王晓宇,男,1977年生,工程师,博 [3 ]OJEDA L,BORENSTEN J.FLEXnav:firzzy bgic expert 士,主要研究方向为移动机器人导航与 rule-based position estmation for mobile robots on rugged 控制、多传感器信息融合与数据处理、 terrain[C]//Proceedings of the 2002 IEEE Intemational 发表学术论文13篇。 Conference on Robotics and Automation Washingion DC, US4,2002:317-322 (4 ]BARSHAN B,DURRANTWHYTE H F.Inertial navigation systems for mobile robots[J].IEEE Transactions on Robot- 闫继宏,女,1974年生,副研究员 ics and Automaton,1995,11(3):328-342 博士,主要研究方向为遥操作机器人系 [5王卫华,熊有伦,孙容磊.一种移动机器人轮子打滑的 统,发表学术论文20篇。 实验校核方法[J1机器人,2005,27(3):197-202 WANGWeihua,XDNG Youlun,SUN Ronglei An experi- mental calibraton method for wheel-slppage in mobile o- bots[J].Robot,2005,27(3):197-202 [6]CHUNG H,OJEDA L.BORENSTEN J.Accurate mobile 徐莉红,女,1973年生,工程师,主 obot dead-reckoning with a precision-calibrated fiber optic 要研究方向为引信设计. gyroscope[J]IEEE Transactions on Robotics and Autma- ton,2001,17(1):80-84 [7]ANTONELLI G,CHAVER NI S,FUSCO G A calibra- tiormethod for odometry of mobile robots based on the least- 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
器人直线越障实验结果验证了该方法能有效地提高 机器人的定位精度 ,降低定位误差. 现阶段仅通过两 轮自平衡机器人的直线越障实验对自控测距法进行 验证 ,下一步还将研究机器人进行平面自由运动、坡 面运动等复杂运动情况下自控测距法的有效性. 参考文献 : [ 1 ]王卫华 , 熊有伦 , 孙容磊. 测程法系统误差的测量与校 核 [J ]. 机器人 , 2004, 26 (5) : 4542460. WANGW eihua, X IONG Youlun, SUN Ronglei. Measure2 ment and calibration of systematic errors of odometry [ J ]. Robot, 2004, 26 (5) : 4542460. [ 2 ]L I Yan, GAO Feng, L IN Tingqi, et al. Study on multi2sen2 sor data fusion for the wheeled mobile robot [C ] / / Proceed2 ings of the 5 th World Congress on Intelligent Control and Automation. Hangzhou, China, 2004: 462324626. [ 3 ]OJEDA L, BORENSTEIN J. FLEXnav: fuzzy logic expert rule2based position estimation for mobile robots on rugged terrain [ C ] / / Proceedings of the 2002 IEEE International Conference on Robotics and Automation. W ashington DC, USA, 2002: 3172322. [ 4 ]BARSHAN B, DURRANT2WHYTE H F. Inertial navigation systems for mobile robots[J ]. IEEE Transactions on Robot2 ics and Automation, 1995, 11 (3) : 3282342. [ 5 ]王卫华 , 熊有伦 , 孙容磊. 一种移动机器人轮子打滑的 实验校核方法 [J ]. 机器人 , 2005, 27 (3) : 1972202. WANGW eihua, X IONG Youlun, SUN Ronglei. An experi2 mental calibration method for wheel2slippage in mobile ro2 bots[J ]. Robot, 2005, 27 (3) : 1972202. [ 6 ]CHUNG H, OJEDA L, BORENSTEIN J. Accurate mobile robot dead2reckoning with a p recision2calibrated fiber op tic gyroscope[J ]. IEEE Transactions on Robotics and Automa2 tion, 2001, 17 (1) : 80284. [ 7 ]ANTONELL I G, CH IAVER IN I S, FUSCO G. A calibra2 tionmethod for odometry ofmobile robots based on the least2 squares technique: theory and experimental validation [J ]. IEEE Transactions on Robotics, 2005, 21 (5) : 99421004. [ 8 ]BORENSTEIN J, FENG L. UMBmark: a benchmark test for measuring odometry errors in mobile robots [ C ] / /1995 SP IE Conference on Mobile Robots. Philadelphia, USA, 1995: 3052311. [ 9 ]BORENSTEIN J, FENG L. Gyrodometry: a new method for combining data from gyros and odometry in mobile robots [C ] / /Proceedings of the 1996 IEEE International Confer2 ence on Robotics and Automation. M inneapolis, MN, USA, 1996: 4232428. [ 10 ]BORENSTEIN J, FENG L. Measurement and correction of systematic odometry errors in mobile robots [ J ]. IEEE Transactions on Robotics and Automation, 1996, 12 ( 6) : 8692880. 作者简介 : 王晓宇 ,男 , 1977年生 ,工程师 ,博 士 ,主要研究方向为移动机器人导航与 控制、多传感器信息融合与数据处理 , 发表学术论文 13篇. 闫继宏 ,女 , 1974年生 ,副研究员 , 博士 ,主要研究方向为遥操作机器人系 统 ,发表学术论文 20篇. 徐莉红 ,女 , 1973年生 ,工程师 ,主 要研究方向为引信设计. ·174· 智 能 系 统 学 报 第 4卷