
第4卷第4期 智能系统学报 Vol.46.4 2009年8月 CAAI Transactions on Intelligent Systems Ag.2009 doi:10.3969/i.i8gn.1673-4785.2009.04.001 一种概率过程神经元网络模型及分类算法 许少华12,李盼池,何新贵2 (1.大庆石油学院计算机与信息技术学院,黑龙江大庆163318:2.北京大学信息科学技术学院,北京100871) 摘要:针对动态信号分类及与先验类别知识融合问题,提出了一种概率过程神经元网络模型.模型将贝叶斯概率 分类机制与过程神经元网络动态信号处理方法相结合,通过在前馈过程神经元网络中增加一个模式单元层,以及采 用归一化指数类型激励函数,实现基于贝叶斯规则的动态信号分类.分析了概率过程神经元网络分类机制与贝叶斯 分类规则的等价性,给出了具体的学习算法,实验结果验证了模型和算法的有效性 关键词:动态信号分类;贝叶斯规则;概率过程神经元网络 中图分类号:TP183文献标识码:A文章编号:16734785(2009)04028305 Combined probabilistic process neural network and classification algorithm XU Shao-hua2,LI Pan-chi',HE Xin-gui2 (1.School of Computer and Information Technology,Daqing Petroleum Institute,Daqing 163318,China;2.School of Electronics En- gineering and Computer Science,Peking University,Beijing 100871,China) Abstract:A probabilistic process neural network has been proposed in order to provide integration of a priori knowl- edge with dynamic information classification.In this model,Bayesian classification was combined with the dynamic information processing of process neural networks.Dynamic information classification based on Bayesian rules was realized by adding a pattern neuron layer and a summing neuron layer to a feed forward process neural network and applying the normalized exponential activation function to the hidden layer.Classification equivalence between probabilistic process neural networks and Bayesian rules was analyzed and a concrete learning algorithm presented. Experimental results showed the effectiveness of the proposed model and algorithm. Keywords:dynamic signal classification;Bayesian rules;probabilistic process neural networks 概率神经网络是由Specht提出的),它与统计易于训练、收敛速度快、适于实时处理等特性,并可 信号处理的许多概念有着紧密的联系,在结构上类 进行任意非线性变换,其判决曲面与最优贝叶斯准 似于反向传播网络,两者的主要区别在于采用以统 则曲面相接近:同时具有很强的容错性,并且各层神 计方法推导的激励函数代替传统神经网络的Sg 经元数目比较固定,因而易于硬件实现等36].目 moid型激活函数.概率神经网络的理论基础是贝叶 前,概率神经网络已广泛应用于模式分类)、信号 斯决策理论,该理论以其独特的不确定性知识表达 处理81、目标跟踪9]等领域中. 形式、丰富的概率表达能力、综合了先验知识的增量 在实际工程领域与科学研究中,存在大量动态 学习等特性,在当前数据挖掘领域被广泛关注.其基 信号模式识别与分类问题,许多系统的输人是依赖 本思想是将已知的类条件概率和先验概率,利用贝 于时间变化的函数.笔者针对动态信号模式分类、故 叶斯公式估计后验概率,然后根据后验概率的大小 障诊断以及动态系统状态预测等时变信息处理问 进行决策分类].许多研究表明概率神经网络具有 题,提出和建立了过程神经元网络理论和模 型1.过程神经元网络可以直接把时变过程作为 收稿日期:200907-16. 输入输出信号,是传统人工神经网络在时间域上的 基金项目:国家自然科学基金资助项目(60572174);黑龙江省教育厅 科学技术研究资助项目(11521013);黑龙江省自然科学基 一种扩展.对于缺乏先验知识和模型的复杂非线性 金资助项目(ZA2006-11);黑龙江省科技攻关资助项目 动态系统的仿真建模、系统辨识、过程模拟以及泛函 (GZ07A103). 通信作者:许少华.E-mail:xush62@163.com. 数逼近等问题,过程神经元网络表现出明显优势,目

284 智能系统学报 第4卷 前已在时变信号的模式识别2】、故障诊断131、预测 准确度.Parzen提出了f(X)的一簇估值公式: 预报4]等许多领域获得成功的应用.文中通过将过 /(x)=日2a(X-x) (4) 程式的时变(函数)信息与文献[1]中的概率神经网 n入1 络相融合,提出和建立了一种过程概率神经网络 同时,Parzen证明了im.(X)-f(x)12=0, (probabilistic process neural networks,PPNN)模型, Cacoullos扩展了Parzen的结果,在Gaussian核 设计了相应的学习算法,实验结果表明该模型及算 的特殊情况下,多变量估计可表达为 法是可行的, 1 1贝叶斯决策相关理论 f(X)=(2m)C 1.1贝叶斯定理 12cp[-(X-x)'(X-X .(5) m 2o2 贝叶斯(Bayes Thomas)在《论机会学说问题的 式中:i表示样本号,m表示训练样本总数,Xs表示 求解》一文中,提出了一种归纳推理的理论,其中的 类别P4的第i个样本,σ表示平滑参数,p表示度量 “贝叶斯定理(或贝叶斯公式)”给出了在已知结果 空间的维数 E后,对所有原因C计算其条件概率(后验概率)的 公式,可以看做是最早的一种统计推断程序.以后被 2概率过程神经元网络 一些统计学者发展为一种系统的统计推断方法,称 在众多时变动态信号处理问题中,受多种非线 为贝叶斯方法.其基本内容是:通过先验概率P(A) 性扰动因素、信号间的耦合作用以及噪声的影响,对 与条件概率P(B1A)来估计后验概率P(A1B),即 于综合评判的结果,不能给出完全精确的肯定(取 P(AI B)=P(BI A)P(A) (1) 值为1)或否定(取值为0)的回答;而往往存在某种 P(B) 程度上的肯定或否定(取值为0~1之间),即评判 1.2贝叶斯判定策略 结果呈现一定的概率性或模糊性.对这类问题的解 用于模式分类的判定规则或策略的公认标准 决,期待着新模型的出现,这种新模型应该既体现评 是:在某种意义上,使预期风险最小.这样的策略称 价结果的概率性,即应与贝叶斯决策理论的判决结 贝叶斯策略.以2类判别为例,设模式状态P为P 果相一致,又能处理各种时变的过程(函数)信号. 或P,欲根据n维向量X=[x1x2…xm]描述 针对这一问题,本节首先提出过程概率神经元的概 的一组测量结果,判定P=P4或P=Pg,贝叶斯判 念,进而提出一种过程概率神经网络模型。 定规则变成: 2.1概率过程神经元模型 d(X)= [Pa,halaf(X)>hglafe(X), (2) 与普通过程神经元模型相似,笔者提出的概率 Lpa,halfa(X)hglafg(X). 过程神经元(probabilistic process neuron,PPN)由时 式中:f(X)和f(X)分别为A和B的概率密度函 变信号输入、时空加权聚合以及激励输出等运算构 数;la为P=Pa时判定d(X)=Pg的损失函数,lg为 成,模型如图1所示. P=Pg时判定d(X)=P4的损失函数(正确判定时 的损失等于0);h4为P=P4的先验概率,hg=1-ha x(ùw() 为P=P的先验概率 x,(ù,(D w.(1) 贝叶斯判定规则d(X)=P4的区域与贝叶斯判 x.()- 定规则d(X)=Pa的区域间的界限可用下式求得 图1概率过程神经元模型 fa(X)Kfa(X). (3) Fig.1 Probabilistic process neuron model 式中:K=hglg/hala: 图1中,x1(t),x2(t),…,xn(t)为时间[0,T]上 使用式(3)的关键是根据样本模式估算概率密度 的过程式输入,0(t),02(t),…,0,(t)分别为各维 函数的能力.通常先验概率为已知,或者可以准确地加 输入的加权函数,y为输出.与普通过程神经元所采 以估计,损失函数需要主观估计.然而若模式的概率密 用的Sigmoid型激励函数不同,该模型采用具有概 度函数未知,并且给出的是一组训练模式(训练样本), 率统计特性的指数型激励函数: 得出概率密度函数的惟一线索只有这些样本 1.3概率密度函数估计方法 (a)exp (6) 判别边界的准确度取决于概率密度函数估计的 式中:σ为平滑参数,0=0.4时,g(x)的分布如图2
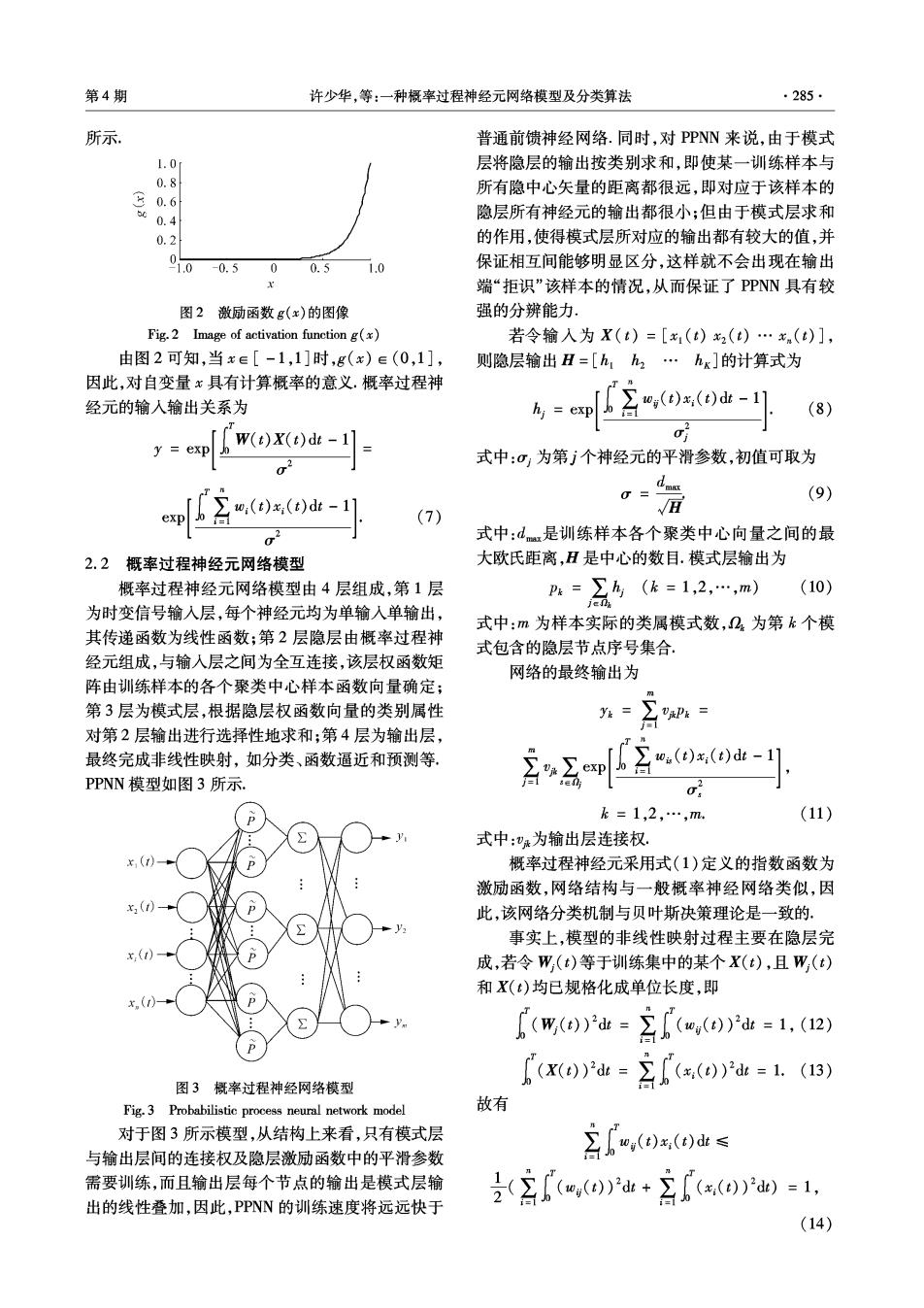
第4期 许少华,等:一种概率过程神经元网络模型及分类算法 285 所示 普通前馈神经网络.同时,对PPNN来说,由于模式 1.0 层将隐层的输出按类别求和,即使某一训练样本与 0.8 所有隐中心矢量的距离都很远,即对应于该样本的 0.6 0.4 隐层所有神经元的输出都很小;但由于模式层求和 0.2 的作用,使得模式层所对应的输出都有较大的值,并 0.5 0 0.51.0 保证相互间能够明显区分,这样就不会出现在输出 端“拒识”该样本的情况,从而保证了PPNN具有较 图2激励函数g(x)的图像 强的分辨能力 Fig.2 Image of activation function g(x) 若令输入为X(t)=[x1(t)x2(t)…x(t)], 由图2可知,当xe[-1,1]时,g(x)∈(0,1], 则隐层输出H=[h,h2…hx]的计算式为 因此,对自变量x具有计算概率的意义.概率过程神 经元的输人输出关系为 h=exp (8) W(t)X(t)dt- o y exp 式中:σ,为第j个神经元的平滑参数,初值可取为 (9) exp (de- (7) o' 式中:d是训练样本各个聚类中心向量之间的最 2.2概率过程神经元网络模型 大欧氏距离,H是中心的数目.模式层输出为 概率过程神经元网络模型由4层组成,第1层 Pk=∑h(k=1,2,…,m) (10) 为时变信号输入层,每个神经元均为单输人单输出, 式中:m为样本实际的类属模式数,2为第k个模 其传递函数为线性函数;第2层隐层由概率过程神 式包含的隐层节点序号集合: 经元组成,与输人层之间为全互连接,该层权函数矩 网络的最终输出为 阵由训练样本的各个聚类中心样本函数向量确定; 第3层为模式层,根据隐层权函数向量的类别属性 y:= 对第2层输出进行选择性地求和;第4层为输出层, 最终完成非线性映射,如分类、函数逼近和预测等。 ∑o,(d)x()d-11 PPNN模型如图3所示. k=1,2,…,m (11) 式中:V:为输出层连接权。 概率过程神经元采用式(1)定义的指数函数为 激励函数,网络结构与一般概率神经网络类似,因 此,该网络分类机制与贝叶斯决策理论是一致的. 事实上,模型的非线性映射过程主要在隐层完 x1) 成,若令W,(t)等于训练集中的某个X(t),且W,(t) 和X(t)均已规格化成单位长度,即 y 【(w)= ∑(0u())2d=1,(12) (x(o)P业= 图3概率过程神经网络模型 oa=LB) Fig.3 Probabilistic process neural network model 故有 对于图3所示模型,从结构上来看,只有模式层 与输出层间的连接权及隐层激励函数中的平滑参数 宫,0x(ea≤ 需要训练,而且输出层每个节点的输出是模式层输 出的线性叠加,因此,PPNN的训练速度将远远快于 客(,o业+店x(0)=1 (14)

286 智能系统学报 第4卷 含,(e(业≥ 的提高.这是由于PPNN模型中,隐层激励函数采用了 具有概率特性的指数函数,同时模式层对隐层输出结 ((,(0)u+a(ou)=-1 果起到了较好的分流作用.PPNN所具有的概率统计特 性提高了对样本模式特征的概括及提取能力. (15) 15 因此 10 (16) 根据激励西数g(☑)=6四]可知,®层 10 10 0 5 10 输出0≤h=g(Z)≤1,求和单元简单地把隐层输出 相累加,然后经加权聚合,在输出层给出[0,1]区间 图4线性交叉数据集聚类样本 的实数值,以确定最终的模式类属,显然输出结果呈 Fig.4 Cluster samples of linear cross dataset 现出一定的概率性, 表1PPNN参数设置 3概率过程神经元网络的学习算法 Table 1 Parameter setting of PPNN PPNN PPN 对于图2所示PPNN模型,可调参数为输出层 输人隐层 U 0 隐层输出层 权值.及隐层平滑参数σ,·定义误差函数为 节点节点选代 步数 学习学习 迭代 学习学习 步数 (dky)2 (17) 速率速率 速率速率 3 101000.8 0.5 1000.60.7 采用梯度下降算法,及σ的调整量计算式为 M 表2PPNN训练结果 aE (18) Table 2 Training results of PPNN aE M 第1类 第2类 (dk-yt)vh× 算法 正确数正确率/% 正确数正确率/% PPNN 99 98.02 96 95.05 (19) PNN 91 90.09 95 94.06 巴及σ的调整计算式为 5 结束语 aE =k-a (20) a 本文提出了一种概率过程神经元网络模型及分 0=0-8 类算法,从神经网络的逼近能力看,该算法可以认为 aoi (21) 是一种确定型算法;但该模型隐层采用具有概率意 义的指数激励函数,使得模型同时具备了随机型算 4 实验分析 法的某些特征,整个模型的推理结构与贝叶斯决策 采用如下数据集:C1:y1=x+6;C2:y2=-x+ 理论相一致.概率过程神经元网络采用过程式输入, 8;-10≤x≤10.其中数据噪声8~V(0,σ2),σ= 有效拓宽了普通概率神经网络的适用范围.由于模 0.1;样本数据采样间隔为△x=0.20.由C1、C2各产 型可调参数少,收敛速度快,因而适合信息的实时处 生101个数据点作为训练样本,如图4所示,样本数 理.实验结果表明,该模型及算法在模式分类方面具 据为2维.为增强样本自身特征,给每类样本增加第 有一定潜力. 3维:z=sg(y)(abs(y)',实验中r=0.01.由于 参考文献: C1和C2在x=0附近交叉,故当x∈[0.4,0.6]时, 分类结果都视为正确。网络参数见表1,训练结果对 [1]SPECHT D F.Probabilistic neural networks for classifica- 比见表2. tion mapping,or associative memory[C]//Proceedings of 实验结果表明,本文建立的PPNN模型与普通 IEEE International Conference on Neural Networks.San Di- PN模型相比,分类的正确数及正确率均有不同程度 eg0,CA,1988:525532

第4期 许少华,等:一种概率过程神经元网络模型及分类算法 ·287· [2]史忠植.神经网络[M].北京:高等教育出版社,2009: procedure neural networks [J].Engineering Science, 203-208. 2000,2(12):4044. [3]SPECHT D F.Probabilistic neural networks J].Neural [11]何新贵,梁久祯,许少华.过程神经网络的训练及其应 Networks,1990,3(1):109-118. 用J].中国工程科学,2001,3(4):31-35. [4]SPECHT D F,SHAPIRO P D.Generalization accuracy of HE Xingui,LIANG Jiuzhen,XU Shaohua.Learing and probabilistic neural networks compared with back propaga- applications of procedure neural networks[].Engineering tion networks[C]//Intemational Joint Conference on Neural Science,2001,3(4):31-35. Networks(IJCNN-91).Singapore:1991:887-892 [12]许少华,刘扬,何新贵.基于过程神经网络的水淹层 [5]蔡曲林.一种新的概率神经网络有监督学习算法[J].模 自动识别系统[J].石油学报,2004,25(4):5457. 糊系统与数学,2006,20(6):8387. XU Shaohua,LIU Yang,HE Xingui.Automatic identifica- CAI Qulin.New supervised leaming algorithm for probabi- tion of water-flooded formation based on process neural net- listic neural network[J].Fuzzy Systems and Mathematics, work[J].Acta Petrolei Sinica,2004,25(4):54-57. 2006,20(6):8387. [13]何新贵,许少华。一类反馈过程神经元网络模型及其 [6]邢杰,萧德云.基于PCA的概率神经网络结构优化 学习算法[J刀.自动化学报,2004,30(6):801806. [J)].清华大学学报:自然科学版,2008,48(1):141-144. HE Xingui,XU Shaohua.A feedback process neuron net- XING Jie,XIAO Deyun.PCA-based probability neural net- work model and its learning algorithm[J].Acta Automati- work structure optimization[J].Journal of Tsinghua Univer- ca Sinica,2004,30(6):801-806. sity:Science and Technology,2008,48(1):141-144. [14]丁刚,钟诗胜.基于时变阚值过程神经网络的太阳 [7]杜吉样,汪增福。基于径向基概率神经网络的植物叶片 黑子数预测[J].物理学报,2007,56(2):1224-1230. 自动识别方法[J].模式识别与人工智能,2008,21(2): DING Gang,ZHONG Shisheng.Sunspot number predic- 206-213. tion based on process neural network with time-varying DU Jixiang,WANG Zengfu.Plant leaf identification based threshold functions[J].Acta Physica Sinica,2007,56 on radial basis probabilistic neural network[J].Pattem (2):1224-1230. Recognition and Artificial Intelligence,2008,21(2):206- 作者简介: 213. 许少华,男,1962年生,博士,教 [8]吴婷,颜国正,杨帮华,等.基于有监督学习的概率神 授,博士生导师.主要研究方向为模式 经网络的脑电信号分类方法[J].上海交通大学学报, 识别、神经网络、智能信息处理.在国 2008,42(5):803-806. 内外学术期刊发表学术论文50余篇, WU Ting,YAN Guozheng,YANG Banghua,et al.Electro- 其中被SCI、EI检索20余篇. encephalography classification based on probabilistic neural network with supervised learning in brain computer interface [J].Joumal of Shanghai Jiaotong University,2008,42 李盼池,男,1969年生,博士,副 (5):803806. 教授,主要研究方向为量子计算、智能 [9]王吴,张波,田蔚风.一种基于概率神经网络多信息 优化算法及其在智能控制、智能信息处 融合的移动目标跟踪算法[J]·上海交通大学学报, 理等方面的应用.在国内外学术期刊 2007,41(5):792-796. 发表学术论文30余篇,其中被SCI、E团 WANG Hao,ZHANG Bo,TIAN Weifeng.A multi-cue 检索10余篇. fused moving object tracker based on probabilistic neural networks J].Journal of Shanghai Jiaotong University, 何新贵,男,1938年生,教授,博 2007,41(5):792-796. 士生导师,中国工程院院士,北京计算 [10们]何新贵,梁久祯.过程神经元网络的若干理论问题[J]· 机学会理事长,《计算机学报》副主编。 中国工程科学,2000,2(12):4044. 主要研究方向为模糊逻辑、神经网络、 HE Xingui,LIANG Jiuzhen.Some theoretical issues on 进化计算、数据库理论,发表学术论文 140余篇,其中多篇被SCI、EI检索