智能系统：带翼水下机器人的非线性拟合分段控制方法

第4卷第3期 智能系统学报 Vol.4 No.3 2009年6月 CAAI Transactions on Intelligent Systems Jn.2009 doi:10.3969/j.issn.16734785.2009.03.011 带翼水下机器人的非线性拟合分段控制方法 庞永杰12，李晔12 (1.哈尔滨工程大学水下机器人技术国防科技重点实验室，黑龙江哈尔滨150001；2.哈尔滨工程大学船舶工程学 院，黑龙江哈尔滨150001)】 摘要：S面控制方法可较好地解决水下机器人的运动控制问题，但由于其参数是固定的，无法达到全局最优.不同 航渡速度段，采取不同的控制参数值，可保证水动力不同阶段控制输出的最优：但在速度变化的分界点，控制器输出 有跳变，不利于系统的全局稳定性.利用T-S模糊系统逼近非线性连续函数的能力，采用非线性的S面函数作为模糊 系统的后件，设计了基于T-S模型的S面控制器.通过T-S模型的引入，避免了控制器输出的跳变，增强了系统稳定 性.将该方法应用于带翼水下机器人的深度控制，水池试验和湖中实验均证明了算法的有效性， 关键词：水下机器人：非线性控制：深度控制：T-S模型：S面控制器 中图分类号：TP24文献标识码：4A文章编号：16734785(2009)03-025806 Nonlinear fitted step control method for a winged micro autonomous underwater vehicle PANG Yong-jie2,LI Ye.2 (1.State Key Laboratory of Autonomous Underwater Vehicle,Harbin Engineering University,Harbin 150001,China;2.College of Shipbuilding Engincering,Harbin Engineering University,Harbin 150001,China) Abstract:The S-surface controller is generally a good tool for motion control of underwater vehicles,yet it cannot reach a global optimum,for its parameters are constants.If different parameters are used at different velocities, control output is optimal at those different hydrodynamic phases.Unfortunately this causes the output of the control- ler to have abrupt changes at the boundaries of velocity subsections,affecting the global stability of the system.To overcome this,a Takagi-Sugeno (T-S)fuzzy model was employed to approach nonlinear continuous functions and the nonlinear S-surface functions were used as the latter of the fuzzy system.On this basis,an S-surface controller was designed.With the introduction of the T-S model,abrupt changes in controller output were avoided,making the system more stable.Experiments in a water tank and lakes proved the validity of the algorithm. Keywords:underwater vehicle;nonlinear control;depth control;T-S model;S surface controller 由于海祥环境的复杂性，以及水下机器人6个D控制的结构相结合，既简化了控制器的设计，又 自由度运动的强非线性和相互耦合，因此水下机器 能保证控制效果.为了加强机器人的自主性与适应 人动力学模型相当复杂.尤其是带有操纵面（舵、翼 性，改善机器人工作性能，刘建成博士等在文献[1] 等)的水下机器人，其运动模型更趋复杂.因此， 的基础上，增加了控制器的积分环节，并将Sigmoid 水下机器人控制系统的设计必须考虑非线性问题和 函数开方，提出亚$面方法).王丽荣博士利用不 不依赖于模型的控制方法.刘学敏博士提出了一种 同类型的S型非线性函数代替Sigmoid函数，提出 结构简单、输入量少、适用于非线性系统的新型控制 了广义S面控制器.S面控制方法原型以及后续 方法—S面控制2.该方法将模糊控制的思想与 的改良型S面控制方法都经过了大量的试验，取得 了较好的控制效果2.但以上方法都是从模糊控 收日期：2008-12-16. 制的思想出发，控制器参数在不同的控制阶段都是 基金项目：国家“863”计划资助项目(2008A4092301):水下机器人技 固定值.随着航速的变化，水下机器人所受的粘性力 术国防科技重点实验室开放课题研究基金资助项目 (2007001). 变化很大.因此控制参数需要随航速变化适时改变， 通信作者：李啡.E-mal:liye@hrbeu.e.cm. 如果采用简单分段函数的形式，那么在速度变化分

第3期 庞永杰，等：带翼水下机器人的非线性拟合分段控制方法 ·259 界点处，控制器输出有跳变，系统不稳定性增加.为 R:if0.5kn<a≤1.0kn: 此本文尝试T-$模糊模型，进行分段控制的非线性 6=2.0/(1.0+e-aae-a0as)-1.0; 拟合.这既保证了控制参数的最优，又保证了系统稳 R3:if1.0kn<w≤1.5kn: 定性 6=20/(1.0+6-aa0)-1.0: 1S面控制方法 R:if1.5kn<w≤2.0kn: 6=2.0/(1.0+0-aa03)-1.0; $面控制方法的控制模型为 R:if2.0kn<u≤2.5kn: r4=20/(1.0+cxp(-kae- 46=2.0/(1.0+e-aa0s)-1.0; ka4)-1.0+△u4, R:if2.5kn<u≤3.0kn: fi=Kiug. o=2.0/(1.0+c-aa01）-1.0. 式中：e:和为第i自由度控制的输入信息（通过归 实验证明：此分段函数可有效解决收敛速度与超 一化处理的偏差和偏差变化率)，：为第i自由度控 调的矛盾，相应的k,和2取值可满足控制要求).但 制输出，ka和k2分别为对应第i个自由度偏差和偏 在速度变化分界点处，控制器输出有跳变这对系统 差变化率的控制参数，△u:为通过自适应方式得到 的稳定性非常不利，尤其对于水下机器人这样的强制 的归一化后的固定干扰力的大小，∫为该自由度上 解耦系统，某一自由度的震荡可引起其他自由度强烈 所需力的大小，K为该自由度上所能提供的最大推 的耦合运动.为了避免这一情况，借鉴模糊控制理论 力与力矩 中的T-$模型，进一步优化了上述规则. 人工调整控制器参数k1和%2，使得在一般情况 下水下机器人的运动控制满足要求.1、k2取得越 3T-S模型的全局最优逼近 大，响应对小偏差的敏感性就越高，但取得太大容易 3.1T-S模型 引起振荡.一般k,和2的初始值选择在3.0左右， 日本学者T.Takagi与M.Sugeno给出了一种模 如果超调大了，可以适当减小1而增加2；反之，如 糊模型表示，它的模糊规则的前件与通常的相同，其 果收敛速度慢了，则可以适当增加1而减小2： 后件不是简单的模糊语言值，而是输入变量的线性 如此就构造了一个简单、实用的水下机器人控 组合8).由于该模糊系统具有高度逼近非线性连 制器，在复杂的海洋环境下该控制器控制效果可以 续函数的能力，因而对它的研究受到人们广泛的 满足作业要求 关注， 2分段函数的引入 Takagi--Sugeno模型（又称T-S模型），它的后件 不是由模糊量表示，而是一个精确函数，即 从控制模型的公式来看，其实际控制参数只有 if x is A and y is B and…,then:=f(x,y,…). 2个(1和2)，需要调整的量就比模糊控制简单得 式中：A,B,…为模糊量；x,y,…为输入过程变量； 多.但对于$面控制器来说，有一点是需要明确的， 八x,y,…)为x,y,…的精确函数. 无论是人工调整还是自适应调整，都不能达到最佳 考虑输入为二维的2条模糊规则及其推理强度为 的匹配；因为这些调整都是全局区域范围内的调整， R():if x is A:and y is Bi, 而没有局部调整功能.无论如何，这里的参数的全局 thcn8=f(x,y,…）,i=1,2; 调整都是对系统的一种近似.毕竟，控制对象的复杂 W=4,(x)Ag,(y) 性和不确定性，使得任何一种函数的全局逼近都有 推理结果的精确量：采用加权平均的方法，为 很大的近似性 Wf(x,y）+W5(x,y） 为此，要达到全局最优的控制效果，不同航渡速 W,+W2 度时，应取不同的控制参数值.在低航速时，希望响 式中f(x,y)常取输入x、y的线性函数： 应快速，因此k1应大，而2小；而在高航速时，为了 f(x,y）=px+9y+r 避免超调和振荡应使减小，而2增大.为此，尝 采用T-S模型的模糊控制器的控制机理在于利 试采用分段函数，以水平翼控制深度为例进行如下 用(x,y)代表的线性系统在输入论域的不同区域 说明： 对非线性控制函数作线性逼近.再利用模糊逻辑的 R:ifu≤0.5kn: 无缝融合能力将各个线性控制器融合起来，整体上 4=2.1/(1.0+e-a21-aa3）-1.0; 逼近系统的非线性控制函数.采用T-S模型的模糊

·260 智能系统学报 第4卷 控制器已经在多个不同的领域得到了成功的应用。 40=2.0/(1.0+eaa)-1.0; 然而，由于其采用是线性函数对被控系统进行分步 R:若航渡速度为负中， 逼近，因此其应用要求被控系统能够完全或近似地 46=2.0/(1.0+e-aa19)-1.0; 局部线性化.对于水下机器人这样的强非线性系统， R:若航渡速度为负大， 简单的采用线性函数进行逼近显然是不合适的.因 0=2.0/(1.0+e-aa0)-1.0; 此后件函数采用已被广泛证实有效的分段精确$面 对航渡速度，取三角形隶属度函数，如图2所示。 函数 3.2T-$模型的平滑过渡能力 y1.0 NL NM NS ZE PS PM PL 设某单输入单输出非线性控制方法定义如下： ry=0.6x+2,x≤6.5； 2.8-2.1-1.4-0.700.71.42.12.8 y=0.2x+9,6.5<x<16; 渡速度a y=0.3x+3,x≤16. 图2隶属度函数 基于T-S模型平滑拟合该算法，得到的模糊规 Fig.2 Membership function 则如下： 这样，通过T-S模型的引人，避免了控制器输出 的跳变，可增强系统控制的稳定性。 R':ifxis then y=0.6x+2; 4T-S/SSC的应用实例 “微龙-1”AUV是为了探索水下机器人微小型 R':ifx is 化而设计的，因而其尺寸小，结构紧凑.由于自身所 510 1417 带能源的限制，只配置了2个主推螺旋桨.艏向控制 then y=0.2x+9; 由2个主推通过推力差产生转艏力矩来实现.通过 尾水平襟翼提供纵倾力矩，控制纵倾，实现升沉来进 R:ifxis 行深度控制. 1619 then y=0.3x+9. 对“微龙-1”进行了模糊非线性分段控制的仿真试 验在定深控制中，将航渡速度采用三角形隶属度函 得到的控制曲线如图1所示的由“o”组成的曲线， 数，分为7个模糊子集{负大，负中，负小，零，正小，正 平滑地连接了上述3条直线. 中，正大}.模糊规则的后件参数k1k2如表1所示. 14- 表1后件函数的参数 0c心 7 Table 1 Latter function parameters 航渡速度/k如 2 NL 0.025 0.047 图1T-$模型平滑过渡分段直线 NM 0.021 0.041 Fig.1 Smooth transition straight lines by T-S model NS 0.021 0.033 3.3基于T-S模型的S面控制器优化 基于上述分析，根据航速段的不同，基于T-$模 0 0.000 0.000 型的S面控制器(T-S/SSC)可定义以下10条规则： PS 0.021 0.033 R:若航渡速度为正大， PM 0.021 0.041 46=2.0/(1.0+e-aa)-1.0; PL 0.025 0.047 R:若航渡速度为正中， 给定系统初态：垂向深度0，纵向速度0.目标位 46=2.0/(1.0+e-aa01)-1.0; 姿：垂向深度2m,纵向速度为1.5kn.系统在采用本 R3:若航渡速度为正小， 章中提出的模糊$面控制和固定参数S面控制的作 6=2.0/(1.0+0-.03)-1.0; 用下的系统响应曲线如图3所示. R:若航渡速度为0， 在初始状态，系统处于纵向速度从0开始加速状 40=0; 态，并下潜.其中，S面控制器SSC1、SSC2、S$C3分别 R:若航渡速度为负小， 对应于偏差变化比例系数大于、等于和小于偏差比例

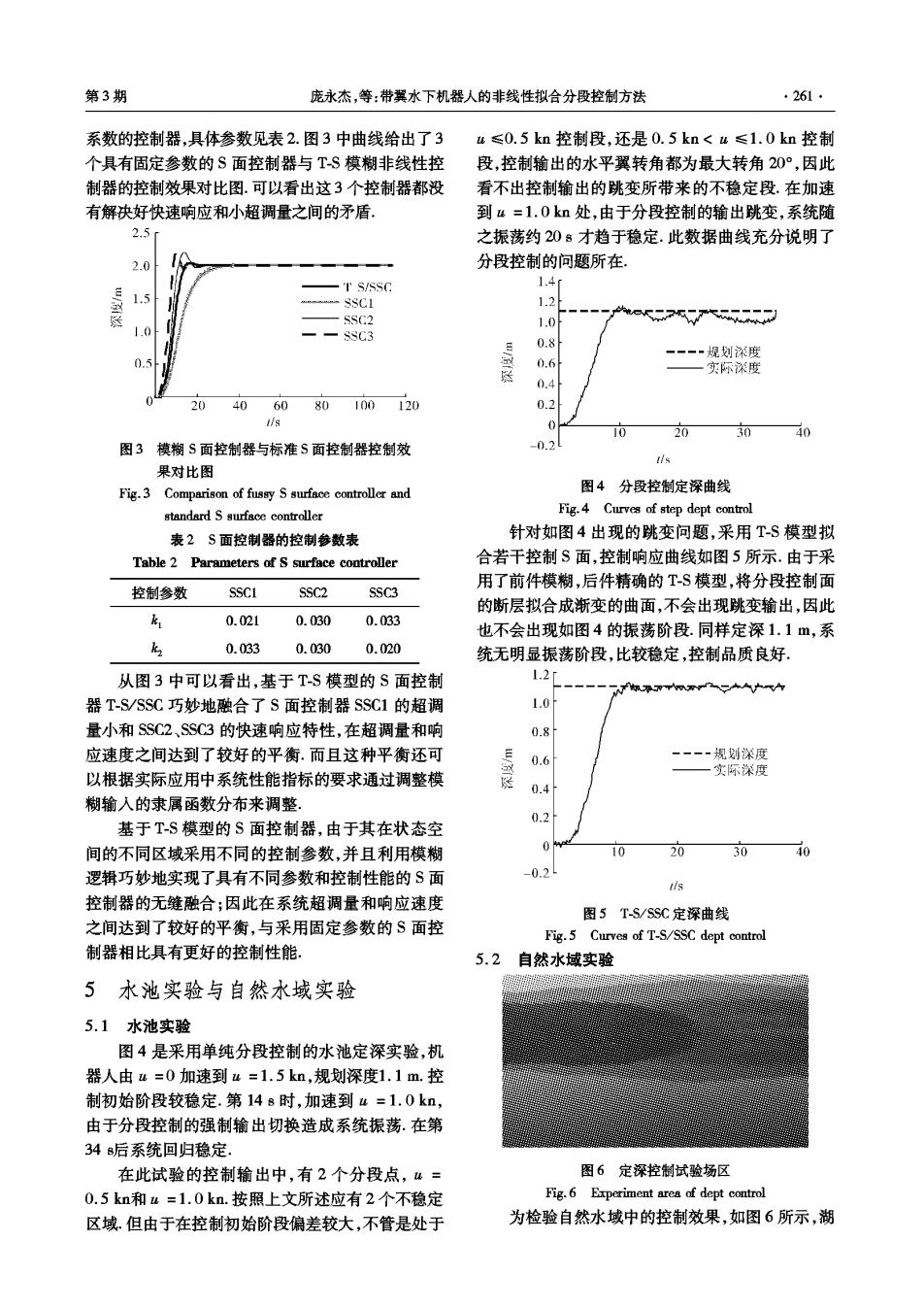
第3期 庞永杰，等：带翼水下机器人的非线性拟合分段控制方法 261. 系数的控制器，具体参数见表2.图3中曲线给出了3 u≤0.5kn控制段，还是0.5kn<u≤1.0kn控制 个具有固定参数的S面控制器与T-S模糊非线性控 段，控制输出的水平翼转角都为最大转角20°，因此 制器的控制效果对比图.可以看出这3个控制器都没 看不出控制输出的跳变所带来的不稳定段.在加速 有解决好快速响应和小超调量之间的矛盾。 到w=1.0k如处，由于分段控制的输出跳变，系统随 2.5 之振荡约20：才趋于稳定.此数据曲线充分说明了 2.0 分段控制的问题所在。 'T S/SSO 1.4 1.5 sSCl 1.2 SSC2 1.0 -SSC3 0.8 一一·规划深度 0.6 一实际深杀度 04 20406080100120 0.2 0 10 20 30 40 图3模糊S面控制器与标准S面控制器控制效 0.2 tls 果对比图 Fig.3 Comparison of fussy S surface controller and 图4分段控制定深曲线 standard S surface controller Fig.4 Curves of step dept control 表2S面控制器的控制参数表 针对如图4出现的跳变问题，采用T-S模型拟 Table 2 Parameters of S surface controller 合若干控制$面，控制响应曲线如图5所示.由于采 用了前件模糊，后件精确的TS模型，将分段控制面 控制参数 SSCI SSC2 SSC3 的断层拟合成渐变的曲面，不会出现跳变输出，因此 k 0.021 0.030 0.033 也不会出现如图4的振荡阶段.同样定深1.1m,系 0.033 0.030 0.020 统无明显振荡阶段，比较稳定，控制品质良好. 从图3中可以看出，基于T-$模型的$面控制 1.2r 器T-S/SSC巧妙地融合了S面控制器SSC1的超调 1.0 量小和SSC2、SSC3的快速响应特性，在超调量和响 0.8 应速度之间达到了较好的平衡.而且这种平衡还可 0.6 一一一·规划深度 一实际深度 以根据实际应用中系统性能指标的要求通过调整模 0.4 糊输入的隶属函数分布来调整， 0.2 基于T-S模型的S面控制器，由于其在状态空 间的不同区域采用不同的控制参数，并且利用模糊 0 10 20 30 40 逻辑巧妙地实现了具有不同参数和控制性能的$面 -0.2 tis 控制器的无缝融合；因此在系统超调量和响应速度 图5T-S/SSC定深曲线 之间达到了较好的平衡，与采用固定参数的$面控 Fig.5 Curves of T-S/SSC dept control 制器相比具有更好的控制性能。 5.2 自然水域实验 5水池实验与自然水域实验 5.1水池实验 图4是采用单纯分段控制的水池定深实验，机 器人由=0加速到w=1.5kn,规划深度1.1m.控 制初始阶段较稳定.第14s时，加速到w=1.0kn, 由于分段控制的强制输出切换造成系统振荡.在第 34后系统回归稳定. 在此试验的控制输出中，有2个分段点，“= 图6定深控制试验场区 0.5kn和a=1.0kn.按照上文所述应有2个不稳定 Fig.6 Experiment area of dept control 区域.但由于在控制初始阶段偏差较大，不管是处于 为检验自然水域中的控制效果，如图6所示，湖

.262 智能系统学报 第4卷 中白色浮标下系一声反射体于水下.“微龙-1”初始 图10是根据GS接收到的位置信息得到的白 在水面航行，并且对准目标.得到指令后，下潜，定深 鹭湖中长距离航行试验的路线.“微龙-1”在不更换 4m水下潜航.利用艏部的前视图像声呐获取目标 能源的情况下，航行12.1km.为了便于监测，长航 声学图像。 没有大深度地下潜，是在近水面进行.湖中试验表 采用分段整定过的S面参数，并利用T-S拟合 明，“微龙-1”在实际水域中有较好的适应性和航行 各曲面得到控制器.将深度控制映射为纵倾控制进 能力，具备在一定航速下定深定向航行的能力， 行定深试验，试验数据曲线如图7所示.定深控制满 29.31 足实验要求.但从图中可以看出，系统响应较慢.这 29.2 是因为定深声学探测水下目标时，要求航速较低，翼 29.1 效不高造成的， 29.0 5.0 28.9 28.8 4.0 规划深坞 28.7 3.0 2.8 23.0 23.223.4 23.623.8 实际深度 东经！(‘) 2.0 图10白鹭湖长距离航行试验路线 1.0 Fig.10 Long distant navigation path in Bailu lake 100 200 300 400 tis 6 结束语 图7T-S/SSC定深4m数据曲线 针对不同航速段采用不同最优控制参数带来的 Fig.7 Data curves of dept 4 m control by T-S/SSC 分段控制边界层系统跳变的情况，采用T-$模型对 采用T-S曲面拟合算法设计的运动控制器在黑 分段函数进行了曲面光顺拟合.这种方法既保证了 龙江省镜泊湖和湖南省白鹭湖分别进行了试验. 变参数S面控制的控制效果，又考虑了系统输出的 图8是在黑龙江省镜泊湖航行实验的现场数据.图9 稳定性.仿真、水池和自然水域实验均证明了算法的 是在湖南省长沙市白鹭湖航行实验的现场数据.由 有效性.本文只是依据经验划分了拟合的分段区间， 于湖试时间的限制，经典的固定参数S面控制器参 关于分段区间的合理性，应深入研究水下机器人水 数和未拟合的分段控制方法并未在实验中尝试.从 动力学原理.这也是需要进一步研究的内容 图中规划深度和实际深度的比较来看，控制器跟踪 性能良好，满足工程需要 参考文献： 1.6 1.4 [1]LI Ye,LIU Jiancheng,SHEN Mingxue.Dynamics model of 1.2 underwater robot motion control in 6 degrees of freedom[J. 1.0 0.8 Journal of Harbin Institute of Technology,2005,12(4): 实际深度 0.6 456459. 0.4 0.3 [2]刘学敏，徐玉如.水下机器人运动的S面控制方法[J] *10 海洋工程，2001,19(3)：8184. 0.21 s LIU Xuemin,XU Yuru.S control of automatic underwater 图8镜泊湖深度控制跟踪曲线 vehicles[J].Ocean Engineering,2001,19(3):81-84. Fig.8 Depth control curves in Jingbo lake [3]刘建成，于华南，徐玉如.水下机器人改进的$面控制 1.6 方法[J].哈尔滨工程大学学报，2002,23(1)：33-36. 1.4 LIU Jiancheng,YU Huanan,XU Yuru.Improved plane .2 L.0 control algorithm for underwater vehicles [J].Journal of 0.8 实际深瘦 Harbin Engineering University,2002,23(1):33-36. 0.6 一·一规划深度 [4]王丽荣.水下机器人控制系统故障诊断研究[D].哈尔 0.4 0.2 滨：哈尔滨工程大学，2006. ×10 0.2 4 WANG Lirong.Rescarch on fault diagnosis for AUV control t/s system[D].Harbin:Harbin Engineering University,2006. 图9 白鹭湖深度控制跟踪曲线 [5]刘建成.水下机器人推进系统故障诊断与容错控制研究 Fig.9 Depth control curves in Bailu lake [D].哈尔滨：哈尔滨工程大学，2004

第3期 庞永杰，等：带翼水下机器人的非线性拟合分段控制方法 .263. LIU Jiancheng.Research on fault diagnosis and fault toler- [9]PANG C T,LUR YY.On the stability of Takagi-Sugeno ant control for actuator of AUV[D].Harbin:Harbin Engi- fuzzy systems with time-varying uncertaintics []IEEE neering University,2004. Transaction on Fussy Systems,2008,16(1):162-170. [6]郭冰洁，徐玉如，李岳明.水下机器人S面控制器的改 作者简介： 进粒子群优化[J].哈尔滨工程大学学报，2008,29 庞永杰，男，1955年生，教授，博士 (12):1277-1282. 生导师，第三、四届海洋工程学会理事 GUO Bingjie,XU Yuru,LI Yueming.S surface controller 主要研究方向为水下机器人总体设计 for underwater vehicles using particle swarm optimization 与运动控制技术.目前主持和参与省部 [J].Journal of Harbin Engineering University,2008,29 级以上科研项目8项，获得国家科技进 (12):1277-1282. 步二等奖1次，国防科学技术一、二、三 [7]LI Ye,ZHANG Lei,WAN Lei,et al.Autonomous under- 等奖各一次.发表学术论文50余篇. water vehicle S-surface controller optimization[].Joumnal 李晔，男，1978年生，副教授.主 of Harbin Institute of Technology,2008,15(3):404-410. 要研究方向为水下机器人规划与运动 [8]HO D W C.SUN Jitao.Stability of Takagi-Sugeno fuzzy de- 控制技术.目前参与省部级以上科研项 lay systems with impulse[J].IEEE Transaction on Fussy 目4项，发表学术论文20余篇 Systems,2007,15(5):784-790. 2009年全国人工智能大会(CAAI-13) 2009 China National Conference on Artificial Intelligence(CAAI-13) 2009年10月25-28日，北京 http://caai.cn/caai-13 为了总结中国人工智能学会CAA-12以来人工智能科学技术的新进展，交流我国科技工作者在该领域的自主创 新成就，推动人工智能及相关学科的理论研究和科技成果转化，中国人工智能学会决定于2009年10月25-28日在 首都北京召开第13届全国学术大会(CA4-13).本届大会由北京航空航天大学承办，北京邮电大学、北京科技大学、 北京理工大学、北京大学、清华大学、北京交通大学、北京工商大学、首都师范大学、北京工业大学等协办 本届大会将邀请著名科学家做高等智能（含脑科学、认知科学、人工智能）前沿报告，举办讲座和专题讨论会， 组织机器人足球、中国象棋机器博弈的竞赛和演示.欢迎中国人工智能学会会员及相关领域的研究人员、高校师 生、企业家、工程技术人员以及一切爱好和有志于智能科学技术事业的朋友踊跃投稿。 重要日期： 征文截止日期：2009年7月20日 录用通知日期：2009年9月1日 出版清样日期：2009年9月20日 优惠注册日期：2009年9月25日前 联系方法： 程序方面：E-mail:caai@bupt.ed.cn 联系人：邹亚茹电话：010-62281360传真：010-62282983 会务方面：E-mail:caai_13@126.com 联系人：刘杨(13581731641)、孟德元(13488684523)