智能系统：个体速度差异的蚁群算法设计及仿真

第4卷第6期 智能系统学报 Vol.4 No.6 2009年12月 CAAI Transactions on Intelligent Systems Dec.2009 doi:10.3969/j.issn.16734785.2009.06.010 个体速度差异的蚁群算法设计及仿真 印峰，王耀南，刘炜2，周良 (1.湖南大学电气与信息工程学院，湖南长沙410082；2.湖南科技职业学院软件学院，湖南长沙410118) 摘要：针对如何提高蚁群算法搜索速度及防止算法停滞问题，提出一种改进的蚁群优化算法VACO(ACO algorithm based on ant velocity),通过构造与局部路径和蚂蚁个体速度相关的时间函数，并建立与时间函数相关的动态信息素 释放机制，加快信息素在较优路径上正反馈过程，从而提高了算法的收敛速度；采取一种连续小区间变异策略，在加 快局部搜索过程的同时可有效防止算法陷入局部最优.对典型TSP问题的仿真研究结果表明，改进后的算法在收敛 性和对较好解的探索性能得到一定程度的提高. 关键词：蚁群算法；旅行商问题；信息素；NP-难解 中图分类号：TP301.6文献标识码：A文章编号：16734785(2009)06052806 Design and simulation of an ant colony algorithm based on individual velocity differences YIN Feng,WANG Yao-nan',LIU Wei2,ZHOU Liang (1.College of Electrical and Information Engineering of Hunan University,Changsha 410082,China;2.School of Software,Hunan Vocational College of Science and Technology,Changsha 410118,China) Abstract:A new implementation of the ant colony optimization (ACO)algorithm was primarily focused on impro- ving search speed and preventing stagnation.To resolve these two issues,improvements based on velocity were pro- posed,producing a VACO algorithm.By constructing a time-function for local paths and ant velocity,and building a dynamic release mechanism for pheromones in the time-function,it accelerated positive feedback from the accu- mulation of pheromones,leading to better paths and improved convergence speed.A strategy of continuous inter- cell mutation sped up local searches and at the same time effectively prevented the algorithm being trapped in local optimums.The results showed that the proposed algorithm improves convergence and increases the possibility of finding optimal solutions. Keywords:ant colony algorithm;TSP;pheromone;NP-hard 蚁群算法是模拟自然界中真实蚁群的觅食行为 以寻找可能存在最优解的解区间，又同时充分利用 而形成的一种模拟进化算法).目前该算法已在求 当前群体的有效信息，使算法搜索的侧重点放在可 解组合优化问题、系统辨识、机器人路径规划、数据 能具有最优解的子区间内：使得算法在可以接受的 挖掘、网络路由等问题时取得了很好的效果231.然 时间内收敛到全局最优解.目前提出的各种改进的 而与其他算法相比，蚁群算法存在搜索速度较慢、容 蚁群算法均围绕对上述问题的研究展开[4刀 易出现停滞现象的缺陷.特别对于大规模优化问题， 信息素更新策略是决定算法收敛速度的关键之 如何加快其收敛速度以及防止算法陷入局部最优一 一，针对如何提高算法收敛速度的问题，目前提出的 直是蚁群算法研究中有待解决的一个热点和难点问 几种有代表性的蚁群政进算法，比如最优保留蚂蚁系 题.总体来说，解决该问题的关键在于如何处理好下 统[4(ASelite)、蚁群系统5)(ACS)、最大-最小蚂蚁 述问题之间的平衡：即使算法的搜索空间尽可能大， 系统[6](MMAS)等，均采用针对全局最优解所属边进 行信息素全局更新的策略，即通过加强对当前最优解 收稿日期：200908-12， 基金项目：国家科技支撑计划资助项目(2008BAF36B01):国家“863” 的利用来缩小算法的搜索空间，进而提高算法的收敛 计划资助项目(2008AA04Z214). 速度.另外也有学者提出动态信息素更新策略89]，其 通信作者：印峰.E-mail:yinfeng83@126.com. 本质也是对蚂蚁所走较优路径上的信息加强的动态

第6期 印峰，等：个体速度差异的蚁群算法设计及仿真 ·529· 调整过程.上述研究结果表明，增加全局最优解的使 过程要快于蚁群2. 用频率，可以使算法获得较好的性能.对较优解的强 2)同一蚁群中蚂蚁个体路径寻优比较. 化有助于加快算法的收敛速度，同时也容易引起停滞 对于以相同速度移动的同一蚁群中的不同个 现象，使算法陷入局部最优.针对该问题，目前提出的 体，选择较短路径ABD移动的个体完成一次巡游的 有效的解决策略可归结于：1)人为限制信息素的总 时间要快于选择较长路径ACD的个体；因此，在相 量，避免路径之间信息素差量过大：2)引入判决因 同时间间隔内，较短路线ABD上积累的信息素更 子，根据定性的分析判断蚁群当前的内部状态，进而 多，其被选择的机会相应更大，随着该过程的继续，2 通过对相关参数的动态调整避免停滞现象⑧，10,3)将 条道路上的信息素数量的差距将越来越大，直至绝 蚁群算法与其他智能方法相结合，在加快局部搜索的 大多数蚂蚁都选择了最短路径 同时提高解的多样性山 通过对于真实蚂蚁路径寻优过程的观察可知， 针对上述问题，本文做了两方面的工作：1)提 其寻优过程的快慢不仅与选择的移动路径有关，而 出一种改进的蚁群算法VACO(AC0 algorithm based 且与其移动速度相关.即有如下关系成立： on ant velocity),通过构造与路径和蚂蚁个体速度相 Search_.time d(i》 vel() (1) 关的时间函数，并建立与时间函数相关的动态信息 素释放机制，使得搜索过程兼顾局部和全局信息，加 式中：d(ii)为2节点连线距离，vel(k)表示第k只 快了在较优路径上信息素正反馈的过程，提高了算 蚂蚁的移动速度.根据式(1)，蚂蚁移动速度越快， 法的收敛速度；2)采取一种连续变异策略，在加快 选择的路径越短，搜索时间就越快.不同于真实蚂蚁 局部搜索过程的同时可有效防止算法陷入局部最 在连续时间内的路径寻优过程，人工蚂蚁采取离散 优.实验结果表明，改进后的算法在收敛性和对较好 的搜索机制，因此不能用蚂蚁速度直接衡量算法寻 解的探索方面得到一定程度的改善， 优的快慢。 1 VACO算法原理分析 由前面分析可知，从整体上观察，完成一次搜索 时间较快的真实蚂蚁个体在移动路径上释放的信息 1.1考虑蚂蚊个体速度的信息素释放机制 素相对较多.如果给人工蚁群设置一个初始“速 以自然界真实蚂蚁路径寻优过程为对象，考虑 度”，并建立某种激励机制使得较优个体“移动速 如下2种情况： 度”呈更快的增长趋势，同时根据式(1)关系构造蚁 1)2组不同速度的蚁群路径寻优比较， 群的路径信息素更新方式，此时可以采用信息素释 日标点 日标点 放量间接描述蚂蚁的寻优速度，据此定义如下的算 法构造规则： d=2 d= d=2. 规则1假设蚁群具有一定的初始速度nitVel, 并且每移动一个步长，第k只蚂蚁的速度增加 △vel(k),其中，蚂蚁速度的增量△vel(k)与路径残 d=2 d d=2 余信息素量成正比.每完成一次迭代计算，对蚂蚁的 ● 速度进行初始化. 起始点 起始点 规则2路径信息素释放量为一个与搜索时间 (a）蚁群1 (h)蚊群2 相关的函数，该函数值由移动路径和蚂蚁速度决定， 图1不同蚁群寻优速度比较 路径长度越短，蚂蚁速度越快，则在该路径上释放的 Fig.1 Comparison of the path optimization speed between 信息素数量越多. different colonies 引入蚂蚁个体运动速度递增的机制，可以加快 如图1所示，在起始点和目标点之间有2条道 信息素在较优路径上信息素正反馈的过程，从而可 路：ABD和ACD,其长度分别为4和6.蚁群1和蚁 以提高蚂蚁的搜索效率， 群2分别以速度1和2匀速移动，并且1>2，假 1.2带变异机制的防停滞策略 设这2种群采取完全相同的路径寻优机制.显然，蚁 根据文献[10,13]，对蚁群算法停滯及相关概 群1完成一次巡游的时间要快于蚁群2，在相同时 念定义如下： 间间隔内，蚁群1在较优路径ABD上信息素的积累 定义1在蚂蚁搜索过程中，由于较好路径上的信 量要大于蚁群2，随着该过程的继续，蚁群1的寻优 息素远大于其他边时，造成所有蚂蚁都选择同样的路

·530 智能系统学报 第4卷 径，即系统不再搜索较好的解，称为停滯现象 如下变异操作规则： 定义2设ra(r,s)、T✉(r,s)分别为与节点r 规则3采用对访问节点序列按排列组合的方 相连的边上最大、最小信息素值，令 法进行编码，即某个巡回路径的染色体是该巡回路 8(r）=Tmm(r,s）-Tn(r,s). 径的节点序列.每完成一次迭代计算，只对当前最优 对某个给定的入(0<入<1)，在所有与节点r相 解进行变异操作 连的边中，信息素量大于A8(r)+Tmi(r,s)的边的 规则4对最优个体重组分区间进行，操作区 数量即为节点r的节点分支数， 间长度取3，变异适度函数取节点连线距离，交换区 定义3设(r)为节点r(r=1,2,…,n)的节点 间内2节点的位置，并比较交换前后区间节点之间 分支数，N为节点总数，则平均节点分支数定义为 的距离和，如果交换后的区间节点之间的距离和小 名职 (2) 于交换前，则交换原节点序列相应2节点位置，否则 保留区间内原节点序列顺序，进行下一个操作区间 由于信息素蒸发的影响，较差解路径上的信息 并重复相同的处理过程. 素量将越来越少，节点上连接边信息素最大值和最 小值的差量将越来越大，根据定义2，节点分支数将 2 VACO算法构造 随之减少.当平均节点分支数趋于2时，意味着所有 1)初始化，设置蚂蚁的初始速度vel=nitVel, 的蚂蚁都选择了同样的路径，即算法出现停滞现象. 用禁忌表abuk记录蚂蚁k当前所走过的节点，a- 如果此时当前解还未达到最优，则说明算法陷入了 lowed.={C-tabu,表示蚂蚁k下一步允许选择的节 局部最优.利用变异算法局部寻优能力强的特点对 点，其中，C为所有节点的集合；其余初始化过程与 当前最优个体进行变异，可加快局部寻优速度，并且 蚁群系统(ACS)算法[3]相同. 有助于算法跳出局部最优， 2)将m只蚂蚁随机分配到n个节点，并将出发 在遗传算法中，变异处理过程一般是先随机地 节点置人禁忌表abuk: 选择2个位置点，然后对区间之间的节点位置按所 3)对处于第i个节点的第k只蚂蚁，依转移概 取适度函数值大小进行重排.为了表现变异过程的 率式(3)[o1选择连接的下一个节点方 随机性，变异操作的区间长度是随机的.然而，区间 长度过大会增加算法搜索的随机性和盲目性，特别 p:(i,j)= 地，对于算法已收敛到局部较优解的情况，变异区间 「arg,ma.r(i)(i》},q≤q(a(t): 较大时很难找到更优解，为此，提出一种效果较为理 ts, 其他 想的连续小区间变异策略：如图2所示，将各节点按 (3) 排列顺序划分为若干个连续子区间，每个区间长度 式中： 取3.以区间i为例，交换b、c2节点的位置显然并 (4) 不影响区间i与外区间节点间的连接关系；现在只 9(A()=(2 n i 需比较交换前后区间内节点距离和大小，即比较 A(t)∈[2，n]表示算法在第t次迭代时的平均节点 D1=D(a,b)+D(c,d)和D2=D(a,c)+D(b,d)的 分支数；n表示节点数；q为[0,1]上分布的随机数； 大小，如果D2<D,说明(acbd)序列组合要优于 (i,)表示节点i与节点j之间的信息素量；n(i,) (abcd),交换原节点序列中b、c的位置，否则保留 表示节点i与节点之间的启发式因子，一般取2节 区间i原节点顺序 点间距离的倒数；B为权重系数. 蚂蚁在选择下一个节点之前先随机生成q,如 果q值小于q(入(t)),则从节点i到所有可行的节 点中找出概率最大的节点，即为下一个要到达的节 图2变异区间划分规则 点；否则按如下概率公式选择下一个节点： Fig.2 Division rules of interval variation P(i,)= 这种局部变异调整后的搜索效率很高，在蚁群 x(i)(i,) 算法迭代前期有助于提高算法的搜索速度；在算法 ,j∈allowed:; r(i,)(i,) 迭代后期，算法陷人局部最优，其宏观表现是蚂蚁的 巡游线路出现局部路径交叉，显然，采取局部调整的 0， 其他 策略对于这一情况的处理是非常有效地.综上，定义 4)修改禁忌表：选择节点后将蚂蚁移动到新的

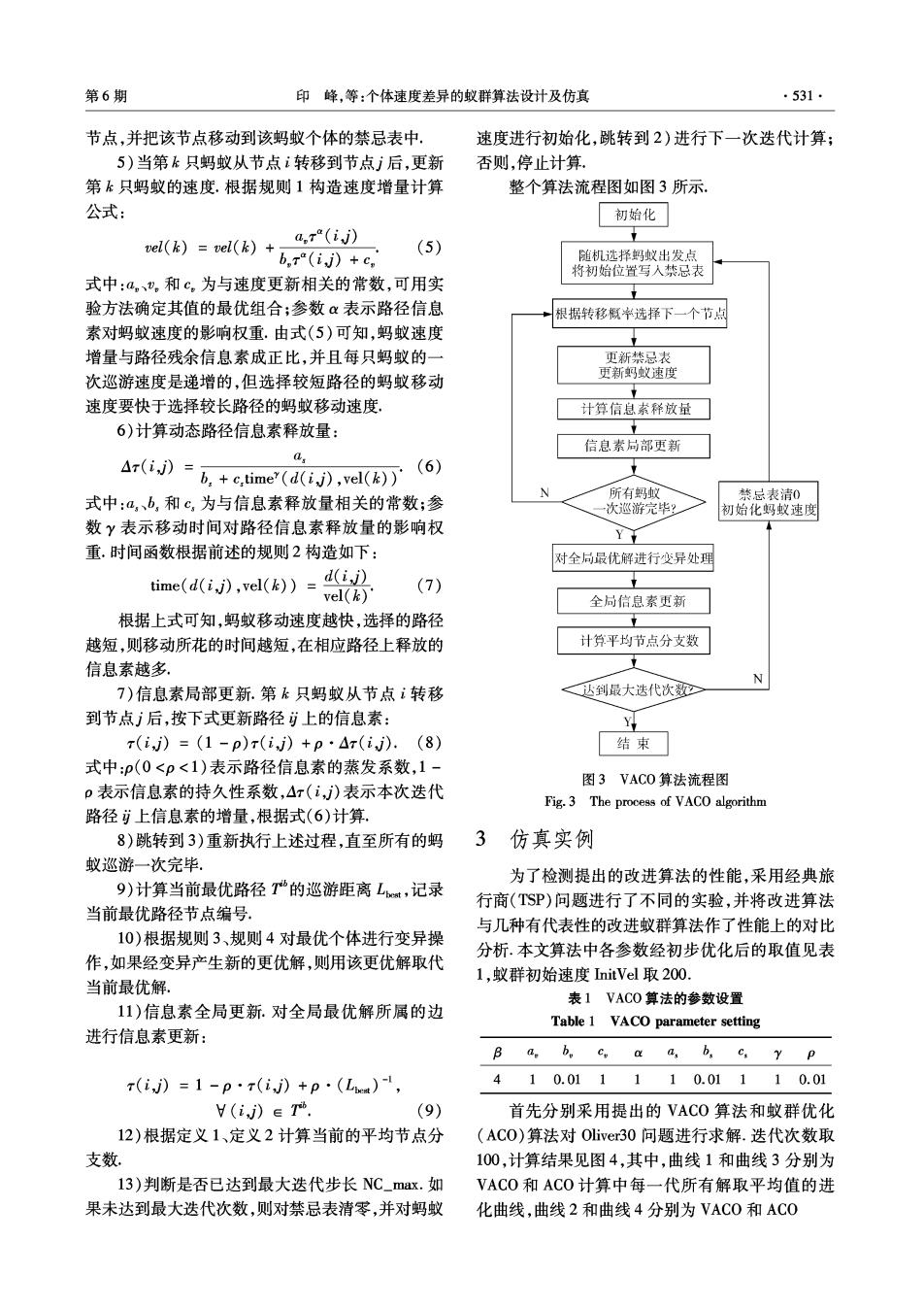
第6期 印峰，等：个体速度差异的蚁群算法设计及仿真 ·531· 节点，并把该节点移动到该蚂蚁个体的禁忌表中， 速度进行初始化，跳转到2)进行下一次迭代计算； 5)当第k只蚂蚁从节点i转移到节点j后，更新 否则，停止计算。 第k只蚂蚁的速度.根据规则1构造速度增量计算 整个算法流程图如图3所示. 公式： 初始化 el(k)=el(k)+,a,r(i） (5) b,r(ij)+c 随机选择蚂蚁出发点 将初始位置写入禁忌表 式中：a,。和c。为与速度更新相关的常数，可用实 验方法确定其值的最优组合；参数α表示路径信息 根据转移概*选择下一个节点 素对蚂蚁速度的影响权重.由式(5)可知，蚂蚁速度 增量与路径残余信息素成正比，并且每只蚂蚁的一 更新禁忌表 次巡游速度是递增的，但选择较短路径的蚂蚁移动 更新蚂蚁速度 速度要快于选择较长路径的蚂蚁移动速度， 计算信总素稀放量 6)计算动态路径信息素释放量： 信息素局部更新 a, Ar(ij)+etime(d(,vel(k))' (6) N 式中：a,、b,和c,为与信息素释放量相关的常数；参 所有蚂蚁 禁忌表清0 次巡游完毕？ 初始化蚂蚁速度 数Y表示移动时间对路径信息素释放量的影响权 Y 重.时间函数根据前述的规则2构造如下： 对全局最优解进行变异处理 ia6,u()= (7) 全局信息素更新 根据上式可知，蚂蚁移动速度越快，选择的路径 越短，则移动所花的时间越短，在相应路径上释放的 计算平均节点分支数 信息素越多. N 7)信息素局部更新.第k只蚂蚁从节点i转移 达到最大迭代次数 到节点j后，按下式更新路径上的信息素： Y r(i,)=(1-p)r(i,j)+p·△r(i).(8) 结束 式中：p(0<p<1)表示路径信息素的蒸发系数，1- 图3VAC0算法流程图 p表示信息素的持久性系数，△r(i,)表示本次迭代 Fig.3 The process of VACO algorithm 路径上信息素的增量，根据式(6)计算. 8)跳转到3)重新执行上述过程，直至所有的蚂 3仿真实例 蚁巡游一次完毕. 为了检测提出的改进算法的性能，采用经典旅 9)计算当前最优路径T的巡游距离L,记录 行商(TSP)问题进行了不同的实验，并将改进算法 当前最优路径节点编号. 与几种有代表性的改进蚁群算法作了性能上的对比 10)根据规则3、规则4对最优个体进行变异操 分析.本文算法中各参数经初步优化后的取值见表 作，如果经变异产生新的更优解，则用该更优解取代 1,蚁群初始速度nit Vel取200. 当前最优解。 表1VACO算法的参数设置 11)信息素全局更新.对全局最优解所属的边 Table 1 VACO parameter setting 进行信息素更新： Ba,b。c。aa,b,c,yp x(i)=1-p·r(i》+p·(La)l, 410.011110.01110.01 H(i,j》eT. (9) 首先分别采用提出的VACO算法和蚁群优化 12)根据定义1、定义2计算当前的平均节点分 (AC0)算法对Oliver30问题进行求解.迭代次数取 支数 100,计算结果见图4，其中，曲线1和曲线3分别为 13)判断是否已达到最大迭代步长NC_max.如 VACO和AC0计算中每一代所有解取平均值的进 果未达到最大迭代次数，则对禁忌表清零，并对蚂蚁 化曲线，曲线2和曲线4分别为VAC0和AC0

·532 智能系统学报 第4卷 计算中每一代最好解的进化曲线， 数内，采用VACO算法计算得到的平均路径值的进 100斤 600r 化曲线收敛性要好于AC0算法，并且呈现出更强的 90 580 560 h线1VAC0 下降趋势，这说明引入速度机制的蚁群算法提高了 70 540 h线3AC0 个体的搜索能力，使得蚁群的整体寻优能力得到 520 定程度的提高.比较图4中曲线2和曲线4可知，在 爸500 有限迭代次数内，采用VACO计算获得的最好解要 40 480 优于AC0算法的计算结果，这说明改进后的蚁群算 20 460F h线2VAC0 法在对最好解的探索能力方面优于AC0算法，同时 10 440.-曲线4AC0 一-▣▣▣。 也间接说明了VACO算法具有更快的寻优速度.另 04 20406080100 420620406080100 外，注意到虽然VACO算法搜索最优解的速度要快 迭代步长 于ACO算法，但在算法搜索的初期，由于函数构造 (a)30城市的实际路径 (b)解的进化曲线 形式和参数选择等原因，其搜索速度优势并未体现 图430城市的实际路径及解的进化曲线 出来.因此，VACO算法本身的构造并不是最优形 Fig.4 The actual path of 30 cities and evolution of solution 式，即便如此，由前面的分析可知，VACO算法整体 curves 由于蚁群中不同个体进化差异以及蚂蚁个体选 性能要优于ACO算法 择路径时具有一定的随机性，因此所有蚂蚁走过路 采用VAC0算法对Eil51问题进行求解，并将 径长度的平均值的进化曲线会产生一定的振荡.另 实验结果与蚂蚁系统(AS)、蚁群系统(ACS)、自适 外，由于蚁群算法属于一种增强型学习算法，因此平 应蚁群算法(AACS)计算结果13]进行比较.最大迭 均路径值进化曲线整体将呈下降的趋势，而各代中 代步数为3000，取连续10次计算结果，并计算其平 最好解的进化曲线将逐渐收敛到最优解或近似最优 均值(Avg)和标准方差(Std.Dev).为便于比较，路 解.比较图4中曲线1和曲线3可知，在有限迭代次 径长度取整数最优解，计算结果见表2 表2不同改进蚊群算法求解E51问题的结果比较 Table 2 Comparison of the solving results between improved ant colony algorithms for the Eil51 算法 1 4 5678910 Avg Std.Dev AS 429432 431429431438432441 435432433.0 3.887 ACS 428429427428427434427430426 427 428.32.312 AACA 428 428427428426 431427 431 426 426427.81.874 VAC0426428 427427 428 426 430428426427427.31.252 80 由表2可知，VACO算法具有更强的发现较好 60 解的能力，10次测试的平均结果也要优于其他算 40 G.p 法；而最小标准方差的取得则说明VACO算法具有 20 较好的计算稳定性.图5反映了VACO算法在一次 10 2030405060 70 典型计算过程中平均节点分支数的变化情况，显然， (a)实际路伦 VACO算法在搜索解的过程中保持了解的多样性， 50 从而有助于防止算法陷入局部最优. 40 根据实验仿真结果可知，引入蚂蚁速度和变异 20 机制的蚁群算法在寻优速度和对较好解的探索方面 10- 500 10001500200025003000 已呈现出一定的优势.但值得注意的是，算法中人工 迭代步长 蚂蚁的“速度”与真实蚂蚁速度是有区别的，真实蚂 (b)平均节点分支数进化曲线 蚁的移动速度越快，其搜索过程就越快；而人工蚂蚁 搜索速度是用有效路径上信息素积累的快慢来衡 图550城市的实际路径及平均节点分支数进化曲线 量.因此，人工蚂蚁“速度”大小并不能直接决定算 Fig.5 The actual path of 50 cities and evolution of average 法搜索的快慢，其初始速度的设置也由算法相关函 node branching

第6期 印峰，等：个体速度差异的蚁群算法设计及仿真 ·533· 数的具体构造形式决定.而引入速度机制的蚁群算 [8]罩刚力，杨家本.自适应调整信息素的蚁群算法[J].信 法其优点正在于加强了有效路径上信息素的正反馈 息与控制，2002,31(3)：199201. 过程. TAN Gangli,YANG Jiaben.An improved ant colony algo- rithm based on adaptively adjusting pheromone[J].Infor 4结束语 mation and Control,2002,31(3):199-201. [9]马溪骏，潘若愚，杨善林.基于信息素递减的蚁群算法 本文从新的角度提出了一种改进的蚁群算法， [J].系统仿真学报，2006,18(11)：3297-3300， 通过构造与蚁群个体“速度”相关的信息素更新机 MA Xijun,PAN Ruoyu,YANG Shanlin.Ant colony algo- 制，并结合变异策略，在一定程度上提高了算法的求 rithm based on pheromone declining[J].Jourmnal of System 解效率和对较好解的探索性能.在对典型TSP问题 Simulation,2006,18(11):3297-3300 仿真研究中，应用本文方法求解取得了较好的效果， [10]DORIGO M,Di CARO G,GAMBARDELLA L M.Ant al- 为蚁群算法研究及其在各种工程问题中的应用提供 gorithms for discrete optimization [J].Artificial Life, 了一个新的思路.目前研究工作还停留在实验阶段， 1999,5(2):137-172. 有关算法本身的构造及相关参数的选取还值得进一 [11]吴庆洪，张纪会，徐心和.具有变异特征的蚁群算法 步研究 [J].计算机研究与发展，1999,36(19)：1241-1245. WU Qinghong,ZHANG Jihui,XU Xinhe.An ant colony 参考文献： algorithm with mutation features[J].Joumal of Computer Research Development,1999,36(19):1241-1245. [1]COLORNI A,DORIGO M,MANIEZZO V,et al.Distribu- [12]朱庆保，杨志军.基于变异和动态信息素更新的蚁群优 ted optimization by ant colonies[C]//Proceedings of Euro- 化算法[J].软件学报，2004,15(2)：186-192. pean Conference on Artificial Life.Paris,1991:134-142. ZHU Qingbao,YANG Zhijun.An ant colony optimization [2]高玮.新型智能仿生模型一蚁群模型[J].智能系 algorithm based on mutation and dynamic pheromone upda- 统学报，2008,3(3)：271-278 ting[J].Joural of Software,2004,15(2):185-192. GAO Wei.The intelligent bionic model-ant colony[J]. [13]黄席樾，张著洪，何传江，等.现代智能算法理论及应用 CAAI Transactions on Intelligent Systems,2008,3(3):271- [M].北京：科学出版社，2005：122-127. 278. 作者简介： [3]段海滨.蚁群算法及其应用[M].北京：科学出版社 印峰，男，1983年生，博士研究 2005:98-101 生，主要研究方向为机器人控制及人工 [4]DORIGO M,MANIEZZO V,COLORINI A.The ant sys- 智能计算。 tem:optimization by a colony of cooperating Agents[J]. IEEE Transactions on Systems,Man,and Cyberetics-Part B,1996,26(1):2941. [5]DORIGO M,GAMBARDELLA L M.Ant colony system:a cooperative learing approach to the traveling salesman 王耀南，男，1957年生，教授，博士 problem[J].IEEE Transactions on Evolutionary Computa- 生导师，主要研究方向为智能机器人、 ion,1997,1(1）:5366. 智能信息处理和智能控制.现任湖南大 [6]BULLNHEIMER B,HARL R F,STRAUSS C.A new rank- 学电气与信息工程学院院长，国家高效 based version of the ant system:a computational study[J]. 磨削工程技术研究中心副主任，教育部 Central European Joumal for Operations Research and Eco. 输变电新技术工程研究中心主任.国际 nomics,1999,7(1):25-38. EEE高级会员，国际自动控制联FAC会员，中国人工智能 [7]周建新，杨卫东，李擎.求解连续函数优化问题的改进 学会、自动化学会、电机工程学会理事.在国内外发表学术论 蚁群算法及仿真[J].系统仿真学报，2009,21(6)：1685- 文200多篇，出版专著和教材4部. 1688. 刘炜，男，1981年生，助教，硕士， ZHOU Jianxin,YANG Weidong,LI Qing.Improved ant 主要研究方向为人工智能 colony algorithm and simulation for continuous function opti- mization[J].Journal of System Simulation,2009,21(6): 1685-1688