智能系统：定位－运输路线安排问题的改进离散粒子群优化算法

第5卷第1期 智能系统学报 Vol.5 No.1 2010年2月 CAAI Transactions on Intelligent Systems Feh.2010 doi:10.3969/i.issn.1673-4785.2010.01.013 定位-运输路线安排问题的 改进离散粒子群优化算法 彭扬，陈子侠，吴承键 (浙江工商大学计算机与信息工程学院，浙江杭州310018) 摘要：定位-运输路线安排问题(LRP)是集成物流中的一个NP-hard难题，为求解一类特殊的LRP问题，提出改进 的离散粒子群优化算法.该方法采用整体优化的思想，将LAP和VP集成在一起.通过合适的粒子编码方式，并改 进粒子的运动方程，引入相应的变异算子和趋同扰动算子等，使得算法的适用性和性能获得了改善.通过仿真实验 及与另2个典型算法的比较分析，证明了该算法的有效性. 关键词：定位-运输路线安排问题；离散粒子群优化；变异算子；进化算法 中图分类号：TP301文献标识码：A文章编号：16734785(2010)01007406 Improved discrete particle swarm optimization algorithm for location-routing problems PENG Yang,CHEN Zi-xia,WU Cheng-jian (College of Computer Science Information Engineering,Zhejiang Gongshang University,Hangzhou 310018,China) Abstract:The location-routing problem (LRP)is an NP-hard problem in integrated logistics systems.An improved discrete particle swarm optimization (PSO)algorithm was developed to tackle a special kind of LRP.It adopted the principle of whole optimization,integrating the location-allocation problem (LAP)with a vehicle routing problem (VRP).First,a novel code for the particle was introduced.Next,the particle's motion equation was improved, and the mutation operator and the disturbing operator against the population identical tendency were proposed, which improved the applicability and performance of the algorithm.A comparison of simulation results with those from two other typical algorithms showed the effectiveness of the proposed method. Keywords:location routing problem;discrete particle swarm optimization;mutation operator;evolution algorithm 物流管理领域一般有3个决策层次：战略层、战LRP是LAP与VRP的集成，目的是根据它们之间 术层和运作层.通常选址与分配问题(location-allo- 的复杂关系来相应地进行物流系统的整体优化 cation problem,LAP)属于战略层次的问题，而传统 LRP显然是NP-hard问题2)，国外有相关的文献阐 的选址分配决策模型不考虑运作层的车辆路径(ve 述其精确算法的求解，但只限于小规模的LRP.启发 hicle routing problem,VRP)、库存控制等问题；但是 式方法似乎是惟一可行的求解实际大规模LRP的 由于选址分配与车辆路径等问题的相互影响，因而 方法，如Tuzun等3)]提出两阶段禁忌启发式算法， 导致结果的次优化现象.定位-运输路线安排问题 Liu[4采用先解决VRP再优化LAP的两阶段启发式 (location routing problem,LRP)正是基于这样的背景 算法，Wu等5应用两阶段模拟退火启发式算法求 产生的，Nag认为LRP不是一个像旅行商问题 解具有多车型且数量给定的LRP问题等，国内张潜 (travelling salesman problem)那样能很好定义的概 等6]提出基于最小包络分析的遗传算法的两阶段 念，它应该被认为是一组问题集合.一般理解 启发式算法，张长星)采用树状编码的遗传算法， 并将LRP作为一个整体而不是分阶段进行求解.由 收稿日期：2008-0630. 于LRP问题的复杂性，各种求解方法都存在一定的 基金项目：国家自然科学基金资助项目(70671096)：浙江省科技计划 重点资助项目(200723090). 局限，探索新的更有效的算法是十分必要的. 通信作者：彭扬.E-mail:pengyang(@mail.jgsu.edu.cm. 粒子群优化算法(particle swarm optimization

第1期 彭扬，等：定位运输路线安排问题的改进离散粒子群优化算法 ·75· PS0)是一种较新的进化计算技术[8]，和遗传算法和 制.或者说本文所研究的是侧重于设施选址分配的 蚁群算法一样，PS0也是一类基于群体智能的随机 层次，它是一类特殊的融合考虑了巡回配送路径的 优化方法.由于该算法具有简单高效的特点，目前已 定位-运输路线安排问题.模型中忽略了实际配送中 广泛应用于函数寻优、神经网络训练、模式分类、模 的一些复杂因素，比如多车型车辆、时间窗约束等 糊系统控制等许多领域.Kennedy和Eberhart)进一 等，相应的数学模型如下所述 步提出了离散二进制版的PS0算法，为解决工程实 1.1基本假设与参数设定 际中的组合优化问题提供了新的方法.Salman[io]通 1)设施（配送中心或仓库、分销中心等）多个， 过适当的粒子编码求解任务指派问题，Tasgetiren I={li=1,2,…,M表示候选设施点的集合，其中 等Ⅲ把连续PS0算法应用到Fow-hop及单一机器 M表示候选设施点的数量，i是设施的编号 调度中.国内李宁等2]用PS0算法求解带时间窗的 2)为了简化计算，假设设施点只进行单车配 车辆路径问题，粒子的位置和速度采用整数表示，运 送，即此时设施点运输工具集合为K={k|k=1,2, 算仍采用连续量的运算法则.钟一文等3]通过重新 …,M},k即表示设施点的运输工具，同时也表示编 定义粒子运算法则，应用离散粒子群优化算法求解 号为k的配送路线，该路线的配送量限制（或车辆 ISP问题.高尚等「4]把遗传算法中的交叉算子和变 装载量)为Qk,该配送容量大于为其分配的运输线 异算子引人粒子位置移动中，提出求解TSP的混合 路上的客户总需求量，而且每辆车供应超过一个客 粒子群优化算法.国内外学者对复杂组合优化问题 户的货物，且每辆车自某个设施点出发，沿着运输路 的尝试解决，也体现了PS0算法在该领域应用的有 线完成配送后必须返回到该设施点， 效性和较好的求解性能， 3)客户集合为J={jj=1,2,…,N},N为所需 借鉴PS0算法求解组合优化问题方面的贡献， 服务的客户数量，J为客户编号.在配送决策中，每个 提出针对一类LRP问题的改进离散粒子群优化算 客户只被一个设施点的某一辆车服务（即从属于一 法.该方法旨在将LAP和VRP进行集成优化，采用 个运输路线)，客户的平均需求量为D,决策结果要 新颖的粒子编码设计，并改进粒子运动方程，以及引 求每个客户的需求得到满足， 入改善算法性能的算子等，实验结果证明了该方法 4)S为配送网络的所有结点集合，S=IUJ, 是有效的， 5)决策的目标是使方案的总成本最小，这里的 1定位-运输问题数学模型 总成本包括设施点的固定设置成本、设施点使用车 辆的租赁（或持有）成本和配送的运输成本，设配送 Nag描述了关于LRP的相关问题背景、模型、 结点间的距离为d:(i,j∈G),从客户结点i到j的单 求解算法以及研究现状等.一般的RP可表述如 位运距运输成本为c:,设施i的设置成本为F:,车辆 下：某公司从一个或多个设施为客户配送货物，客户 k的租赁（或持有）成本为Gk· 的数量、位置、需求量已知或可估计出，设施为工厂、 1.2 模型中的决策变量 仓库、分销中心等，现有若干个设施的位置可供选 「1，设施点的车辆k从结点i行行驶j, X= 择，但每个客户仅从一个设施得到货物，即在一定的 l0, 其他； 时间内，每个客户仅被运输车辆访问一次21.需要 Yy= 1,客户j被分配给设施i服务， 解决的问题是：在满足一定约束条件下，1)选择设 l0, 其他； 施的位置和数量；2)确定最佳的运输行程路线，使 Z= 1,设施点i被选择， 得总费用最低.总费用指设施的建设成本、运作成本 l0, 其他。 以及车辆的固定成本、运输成本等.约束条件包括： 为计算需要，增加辅助变量A2,l∈J,k∈K,且A4≥ 设施和运输车辆的容量和数量的限制、交货时间窗 0.该变量的引入是为了消除路线k中的子回路， 口限制等 1.3模型建立 如Na罗所述，LRP问题是集成2个层次的物流 模型式(1)中的目标函数有3项组成，分别表 决策问题，在实际应用中，可有不同的问题背景和侧 示配送成本、设施设置成本和车辆的持有成本，式 重.考虑到小批量、多频度配送是现代物流的一个特 (2)表示每个客户都有且只有一个设施为之服务， 征，本文所研究的是有多个候选设施，每个设施每次 式(3)表示配送路线的容量（运输工具装载量）约 可使用一辆具有一定装载量限制的车辆进行配送， 束，式(4)保证路线的连续性，式(5)消除配送路线 而车辆装载量这里也可以看成是设施的服务容量限 中的子回路，式(6)保证每个运输工具要么不被使

·76 智能系统学报 第5卷 用，要么只从某一个设施点发出，式(7)保证客户只 序编号 被已选择开设的设施服务，该设施将决定某一个配 定义1客户点有一个可以为之服务的设施 送路线。 集合，某设施对该客户的吸引度定义为：= )=im名名X+ 二，其中d=nxd(》即为到达客户点j Ar2,+Ac,A月 (1) kek iel jej 的最远设施距离，da=mind(i,j)表示为到达客户 subject to AA=l,听e (2) 点的最近距离，显然0≤5：≤1. 2.3粒子的变异策略 月马gX≤0，keK: (3) 为了使粒子更新有较好的全局探索能力，特别 名4-Aa=0, 是后期粒子趋同性更显著时，通过设施的开放与关 闭操作可以产生一些新粒子，来增加优化算法跳出 Hk∈K,p∈S; (4) 局部极值的能力. Uk-Uk+Nx≤N-1, 1)设施增加开放变异算子 l,j∈J,k∈K; (5) 从候选的未开放的设施中随机开放一个设施， 名A≤1，Vke: (6) 根据最近距离服务优先策略，选择服务客户，并将该 ∑(X+X)-乙g≤1， 客户从原服务设施处删除，更新粒子编码. p 2)设施减少开放变异算子 i∈I,jeJ,keK (7) 对当前某粒子编码，选择服务客户少的设施进 2混合粒子群优化算法 行关闭，并将该设施原服务客户按设施吸引度依次 插入相应设施服务集合中（插人时考虑设施容量约 2.1粒子群优化算法 束)，插入点设置为该服务序列中最接近的客户点 在粒子群优化算法中，每个粒子都代表着搜索 的后面 空间的一个可行解，所有的粒子都有一个根据目标 2.4粒子的运动方程 函数计算的适应值以及在解空间中所处的位置x和 本文提出的改进离散PS0算法将修改粒子的 速度”.粒子跟踪2个极值：粒子群整体找到的当前 运动方程，将式(8)中的速度惯性0，部分去掉，将 最优解gm和单个粒子本身找到的最优解p,通 个体学习部分c1rand(·)(pt-x,)和社会学习部 过以下的粒子运动方程来更新和迭代进化. 分c2rand(·)(gem-x,)替换为粒子针对个体历史 Vi+=wV:+cirand()(pbemt -x,)+ 最优位置和全局最优位置的交叉操作，其中c1、c2 c2rand(·)(g-x), (8) 按照离散版粒子群优化算法的本意是一种概率选 x4l=x,+y+1 (9) 择，这里沿用其思想.同时，首先将原始粒子群划分 在式(8)中，粒子速度更新表达式的第1部分为粒 为多个有部分粒子重叠的子群，每个子群会产生一 子先前的速度；第2部分为“认知(cognition)”部分， 个局部的历史最优位置(local best),记为xem,粒子 表示粒子本身的思考；第3部分为“社会(social)” 飞行时共享所在子群的x和全体粒子群的历史最 部分，表示粒子间的信息共享与相互合作8] 优位置x,调整当前位置，产生下一代位置向量. 2.2粒子编码方式 改进的粒子运动方程为 借鉴文献[9]的粒子编码方法，采用三维的粒 x+1=0x:①ax1hem⊕Bxgbt: (10) 子编码表示方法，即 粒子的运动方程按照粒子当前位置、粒子所在 {(a1,b1,c1),(a2,b2,c2）,…,(aw,bw,cn)} 子群的历史最优位置和全部粒子的历史最优位置进 或 行依据隶属度的“⊕”操作，这里的“⊕”有2层（有 /a1,a2,…,a,,aw 先后顺序)的定义： b1,b2,…,b:,…,bw 1)关于客户-设施的隶属度合成. C1,C2,…,C,…,Cw 定义隶属度中为一个0到1间的实数，表示设 的编码形式，其中第一维(a1,a2,…,aw)表示客户编 施i服务客户j的概率，隶属度越大表明客户被该设 号，(b1,b2,…,bw)表示客户对应的设施编号，(c1, 施服务的可能性越大.粒子编码中某设施服务的客 c2,…,cw)表示客户在设施所服务的配送路径中顺 户集合的所有客户，其对应的客户服务于设施的隶

第1期 彭扬，等：定位运输路线安排问题的改进离散粒子群优化算法 ·77 属度为1，经过权重因子w、αB的作用后，客户服务 定义3粒子群的多样性可以通过粒子趋同度 于设施的隶属度被更新，按照隶属度的大小排序，确 认为设施所服务的客户集合；同时考虑设施的服务 p来测度p-名（®e）.显然ee【0,1,这 容量，如果最大隶属度的设施容量溢出，则依次考虑 里N表示粒子群规模， 次大隶属度的设施，完成客户点对设施的重新分配， 趋同扰动算子是在粒子趋同度下降到一定程度 即LA(location-allocation)部分. 时，按概率在粒子群中随机选择一些粒子，仿照初始 2)关于客户在设施服务序列中的顺序合成与 化粒子群的方法产生同样数量的粒子进行置换， 更新. 2.6算法流程 粒子编码中，每个客户在相应的设施中都有一 应用改进离散粒子群优化算法解决定位分 个服务的顺序数，在3个粒子（当前粒子位置x,、子 配运输路径问题的实现步骤为 群历史最优位置xm、粒子群历史最优位置xt) 1)设定参数，粒子种群规模，最大迭代次数，粒 经过权重因子、B的加成后，在已经确认的设施 子运动方程的3个权重因子；设定划分粒子子群数 服务的客户集合中，对其中每个客户的加成后的顺 和重叠粒子数，粒子增加设施开放变异率日，和关闭 序数（这时为实数）进行整数规范，并按从小到大排 设施变异率02；设定粒子趋同度阀值p和趋同扰动 序，得到更新后的顺序数. 算子粒子选择概率03. 例如，设8个客户点，4个候选设施，t时刻某粒 2)初始化操作. 子位置编码以及子群最优和全局最优的粒子位置编 设P为满足客户需求的最小设施数，随机选 码分别为 择p(这里p≥P,且p≤M)个设施开放服务，按设 23516748 施对客户的吸引度，依次插入客户点并保证满足设 x。= 11122233 施服务容量约束，如果某设施点服务的客户集合为 21313221 空，则关闭该设施.对于设施服务的客户集合，随机 /35672418Y 产生设施服务序列 11112233 3)划分粒子群的子群，并评价每个粒子的适应 13421221 度，得到每个子群的初始xt,并将种群中最高适应 23615748 值的粒子位置设为rea r中eat 11122233 4)更新粒子位置并评价， 21323121 根据粒子运动方程，更新粒子位置；计算粒子适 应值，更新各子群的xe和全局的re 设0=0.3，a=0.3,B=0.4,阈值0=0.5，在设施容 5)变异和趋同扰动. 量约束没有冲突（即只考虑最大隶属度）的情况下， 对每个粒子产生[0,1]间的随机数c1和c2,如 得到粒子位置的更新为 果c1>01则该粒子进行增加设施开放变异操作，并 23561748 同时判断如果c2>02则该粒子进行关闭设施变异 +曰 11112233 操作，产生新粒子； 21342121 计算粒子发散度”，如果”大于粒子趋同度阀 2.5 趋同扰动算子 值P,则按照趋同扰动算子的粒子选择概率选择 在进化过程中，由于粒子运动方程的作用，粒子 一定量的粒子进行趋同扰动操作，产生一批新粒子 趋同性越来越显著，而多样性则迅速下降，为了克服 并更新粒子群， 优化算法的早熟和易于陷入局部极值的缺陷，引入 6)判断是否满足终止条件或达到最大迭代次 趋同扰动算子来增加算法的全局优化能力. 数，是则进化停止并转下一步；否则回4)，重复执 定义2 粒子位置的“异或”操作，以符号“☒” 行粒子群更新. 运算表示。 7)解析粒子编码，得到近似最优解(LA和VRP x:☒x,= 2部分的)和目标函数值. r1,x:=x,这里的“=”表示2个粒子 位置向量完全一致； 3算例分析 0. 其他。 为了分析算法的有效性及可行性，本文使用

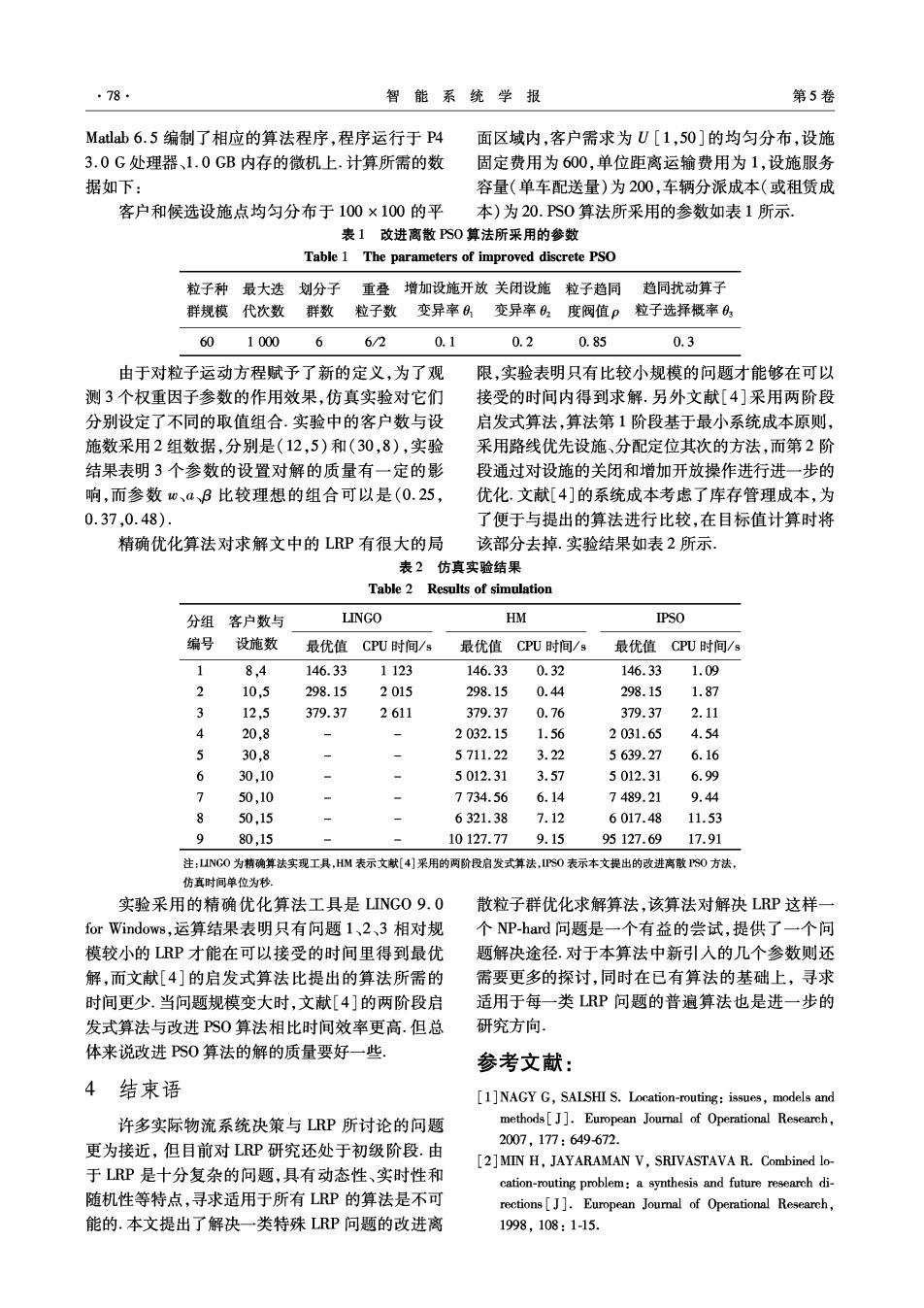
·78 智能系统学报 第5卷 Matlab6.5编制了相应的算法程序，程序运行于P4 面区域内，客户需求为U[1,50]的均匀分布，设施 3.0G处理器、1.0GB内存的微机上.计算所需的数 固定费用为600，单位距离运输费用为1，设施服务 据如下： 容量（单车配送量）为200，车辆分派成本（或租赁成 客户和候选设施点均匀分布于100×100的平 本)为20.PS0算法所采用的参数如表1所示. 表1改进离散PS0算法所采用的参数 Table 1 The parameters of improved discrete PSO 粒子种最大迭划分子重叠增加设施开放关闭设施粒子趋同 趋同扰动算子 群规模代次数群数粒子数变异率8变异率6，度阀值p粒子选择概率0， 60 1000 6 6/2 0.1 0.2 0.85 0.3 由于对粒子运动方程赋予了新的定义，为了观 限，实验表明只有比较小规模的问题才能够在可以 测3个权重因子参数的作用效果，仿真实验对它们 接受的时间内得到求解.另外文献[4]采用两阶段 分别设定了不同的取值组合.实验中的客户数与设 启发式算法，算法第1阶段基于最小系统成本原则， 施数采用2组数据，分别是(12,5)和(30,8)，实验 采用路线优先设施、分配定位其次的方法，而第2阶 结果表明3个参数的设置对解的质量有一定的影 段通过对设施的关闭和增加开放操作进行进一步的 响，而参数w、aB比较理想的组合可以是(0.25， 优化.文献[4]的系统成本考虑了库存管理成本，为 0.37,0.48). 了便于与提出的算法进行比较，在目标值计算时将 精确优化算法对求解文中的LRP有很大的局 该部分去掉.实验结果如表2所示. 表2仿真实验结果 Table 2 Results of simulation 分组客户数与 LINGO HM IPSO 编号 设施数 最优值CPU时间/s 最优值CPU时间/s 最优值CPU时间/s 1 8,4 146.33 1123 146.33 0.32 146.33 1.09 2 10,5 298.15 2015 298.15 0.44 298.15 1.87 3 12,5 379.37 2611 379.37 0.76 379.37 2.11 4 20,8 2032.15 1.56 2031.65 4.54 30,8 5711.22 3.22 5639.27 6.16 6 30,10 5012.31 3.57 5012.31 6.99 7 50,10 7734.56 6.14 7489.21 9.44 50,15 6321.38 7.12 6017.4811.53 9 80,15 10127.77 9.15 95127.6917.91 注：山NC0为精确算法实现工具，HM表示文献[4]采用的两阶段启发式算法，IS0表示本文提出的改进离散S0方法， 仿真时间单位为秒 实验采用的精确优化算法工具是LING09.O 散粒子群优化求解算法，该算法对解决LRP这样一 for Windows,运算结果表明只有问题1、2、3相对规 个NP-hard问题是一个有益的尝试，提供了一个问 模较小的LRP才能在可以接受的时间里得到最优 题解决途径.对于本算法中新引入的几个参数则还 解，而文献[4]的启发式算法比提出的算法所需的 需要更多的探讨，同时在已有算法的基础上，寻求 时间更少.当问题规模变大时，文献[4]的两阶段启 适用于每一类LRP问题的普遍算法也是进一步的 发式算法与改进PS0算法相比时间效率更高.但总 研究方向。 体来说改进PS0算法的解的质量要好一些. 参考文献： 4结束语 [1]NAGY G,SALSHI S.Location-routing:issues,models and 许多实际物流系统决策与LRP所讨论的问题 methods[J].European Joural of Operational Research, 2007,177:649672. 更为接近，但目前对LRP研究还处于初级阶段.由 [2]MIN H,JAYARAMAN V,SRIVASTAVA R.Combined 1o- 于LRP是十分复杂的问题，具有动态性、实时性和 cation-routing problem:a synthesis and future research di- 随机性等特点，寻求适用于所有LRP的算法是不可 rections[J].European Joural of Operational Research, 能的.本文提出了解决一类特殊LRP问题的改进离 1998,108:1-15

第1期 彭扬，等：定位运输路线安排问题的改进离散粒子群优化算法 ·79· [3]TUZUN D,LAURA I.A two-phase tabu search approach to Systems Engineering-Theory Practice,2004,4:130- the location routing problem[J].European Joural of Oper- 135. ational Research,1999,116:87-99. [13]钟一文，杨建刚，宁正元.求解TSP问题的离散粒子群 [4]LIU S C,LEE S B.A two-phase heuristic method for the 优化算法[J].系统工程理论与实践，2006,6：88-94. muti-facility location routing problem taking inventory con ZHONG Yiwen,YANG Jiangang,NING Zhengyuan.Dis- trol decisions into consideration[J].The International Jour crete particle swarm optimization algorithm for TSP problem nal of Advanced Manufacturing Technology,2003,22:941- [J].Systems Engineering-Theory Practice,2006,6: 950. 88-94 [5]WU Taihis,LOW Chinyao,BAI Jiunnwei.Heuristic solu- [14]高尚，韩斌，吴小俊，等.求解旅行商问题的混合粒 tion to multi-facility location-routing problems[J].Comput- 子群优化算法[J].控制与决策，2004,19(11)：1286- ers Operations Research,2002,29:1393-1415. 1289. [6]张潜，高立群，刘雪梅，等.定位运输路线安排问题的 GAO Shang,HAN Bin,WU Xiaojun,et al.Solving trave- 两阶段启发式算法[J].控制与决策，2004,19(7)：773 ling salesman problem by hybrid particle swarm optimiza- 777. tion algorithm[J].Control and Decision,2004,19(11): ZHANG Qian,GAO Ligun,LIU Xuemei,et al.A two- 1286-1289. phase heuristic approach to the location routing problem 作者简介： J].Control and Decision,2004,19(7):773-777. 彭扬，男，1971年生，副教授、博 [7]张长星，党延忠.定位-运输路线安排问题的遗传算法研 士，主要研究方向为物流系统优化、计 究[J].计算机工程与应用，2004,12：6568. 算智能等.主持和参与国家及省部级科 ZHANG Changxing,DANG Yanzhong.A novel genetic al- 研项目10余项，发表学术论文20余 gorithm for location-routing problem[J].Computer Engi- 篇，其中被EI、STP检索9篇. neering and Application,2004,12:65-68. [8]KENNEDY J,EBERHART R C.Particle swarm optimiza- tion[C]//Proceedings of the IEEE International Conference 陈子侠，男，1962年生，教授，浙江 on Neural Networks.Piscataway,USA,1995:1942-1948. 工商大学计算机与信息工程学院副院 [9]KENNEDY J,EBERHART R C.A discrete binary version 长，浙江工商大学现代物流研究所所 of the particle swarm algorithm [C]//Proceedings of the 长，中国物流学会常务理事.主要研究 World Multiconference on Systemics,Cybernetics,and In- 方向为物流系统工程、信息管理与信息 formatics.Piscataway,USA,1997:4104-4109. 系统等.主持或主要参与省部级纵向研 [10]SALMAN A,AHMAD I,AL-MADANI S.Particle swa- 究课题3项，承担中国第一汽车集团公司等企业横向研究项 rm optimization for task assignment problem[J].Micro- 目20余项.曾获中国物流与采购科技进步二等奖、中国商业 processors and Microsystems,2002,26(8):363-371. 科学技术进步二等奖、浙江省第十二届哲学社会科学优秀成 [11]TASGETIRE M F,SEVKLI M,LIANG Y C,et al.Parti- 果奖三等奖、中国汽车工业科技进步奖、中国物流学会年会 cle swarm optimization algorithm for permutation flowshop 论文二等奖、杭州市自然科学优秀论文二等奖等.发表学术 sequencing problem[C]//Proceedings of the 2004 Con- 论文40余篇，出版专著、编著5部. gress on Evolutionary Computation.Portland,USA,2004: 吴承键，男，1957年生，教授、博士， 536-541. 主要研究方向为物流与供应链管理、地 [12]李宁，邹形，孙德宝.带时间窗车辆路径问题的粒 理信息系统等.曾参加和主持多项省部 子群算法[J].系统工程理论与实践，2004,4：130- 级重点科研项目，获得省部级奖项6 135. 次.发表学术论文20余篇，其中被SC1、 LI Ning,ZOU Tong,SUN Debao.Particle swarm optimi- EI检索5篇，出版专著、编著3部. zation for vehicle routing problem with time windows[J