
第三章习题讲解 2024/10/21
第三章习题讲解 2024/10/21 1

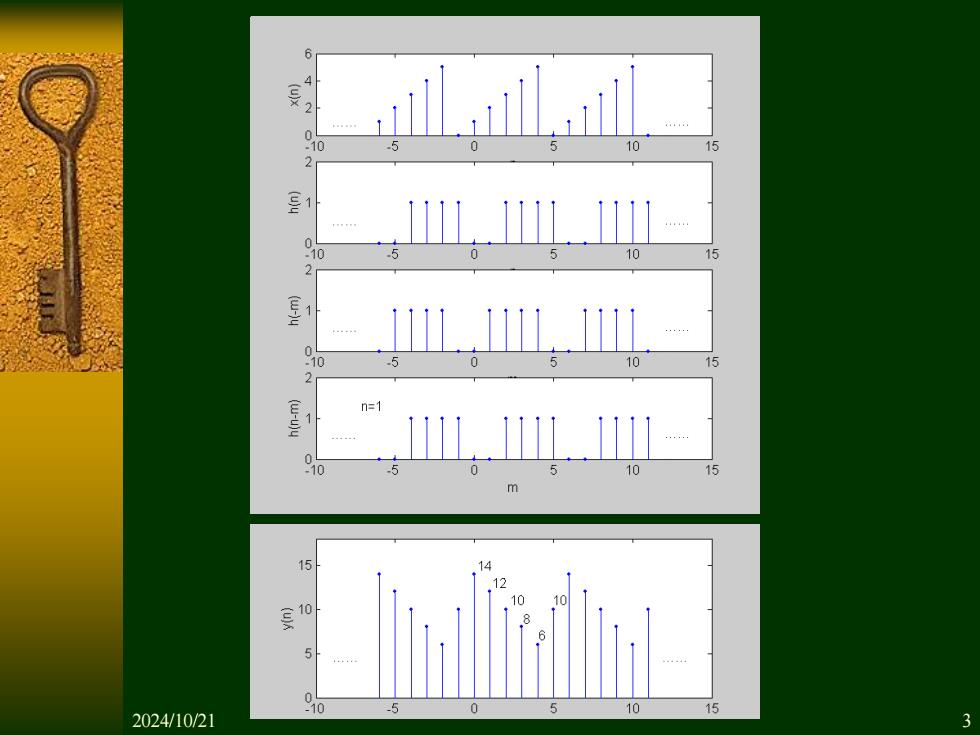
3.设x0- n+1,0≤n≤4 0, h(n)=R,(n-2) 其他n 令x(n)=x(n)6,h(n)=(n)。, 试求(n)与h()的周期卷积并作图。 解: m=∑i(m)hn-m) m=0 2024/10/21 2
1, 0 4 ( ) 0, n n x n n + = 其他 3.设 4 h n R n ( ) ( 2) = − 令 x n x n ( ) (( )) = 6 , h n h n ( ) (( )) = 6 , 试求 x n( ) 与 h n( ) 的周期卷积并作图。 解: 1 0 ( ) ( ) ( ) N m y n x m h n m − = = − 2024/10/21 2
6 2 L 10 L11 .10 15 10 15 10 15 12 10 10 15 2024/10/21 3
2024/10/21 3
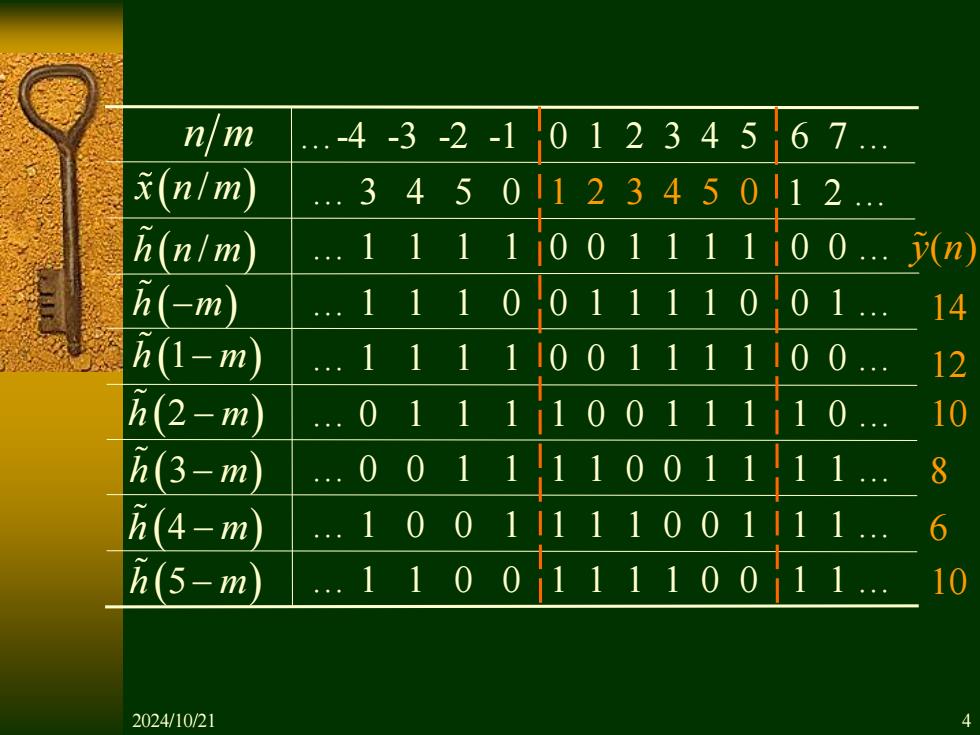
nm 4-3-2-1101234567 x(n/m) .34501123450112 (nlm 111110011110 0 i(-m) .1110 11110 n(1-m .11111001 h(2-m) 0 11 (3-m) 001 8 (4-m) 0 0 6 (5-m 0 2024/10/21
. 1 1 0 0 1 1 1 1 0 0 1 1 . . 1 0 0 1 1 1 1 0 0 1 1 1 . . 0 0 1 1 1 1 0 0 1 1 1 1 . . 0 1 1 1 1 0 0 1 1 1 1 0 . . 1 1 1 1 0 0 1 1 1 1 0 0 . . 1 1 1 0 0 1 1 1 1 0 0 1 . . 1 1 1 1 0 0 1 1 1 1 0 0 . . 3 4 5 0 1 2 3 4 5 0 1 2 . n m .-4 -3 -2 -1 0 1 2 3 4 5 6 7 . x n m ( / ) h m (− ) h m (1− ) h m (2 − ) h m (3− ) h m (4 − ) h m (5 − ) h n m ( / ) 14 12 10 8 6 10 y n( ) 2024/10/21 4
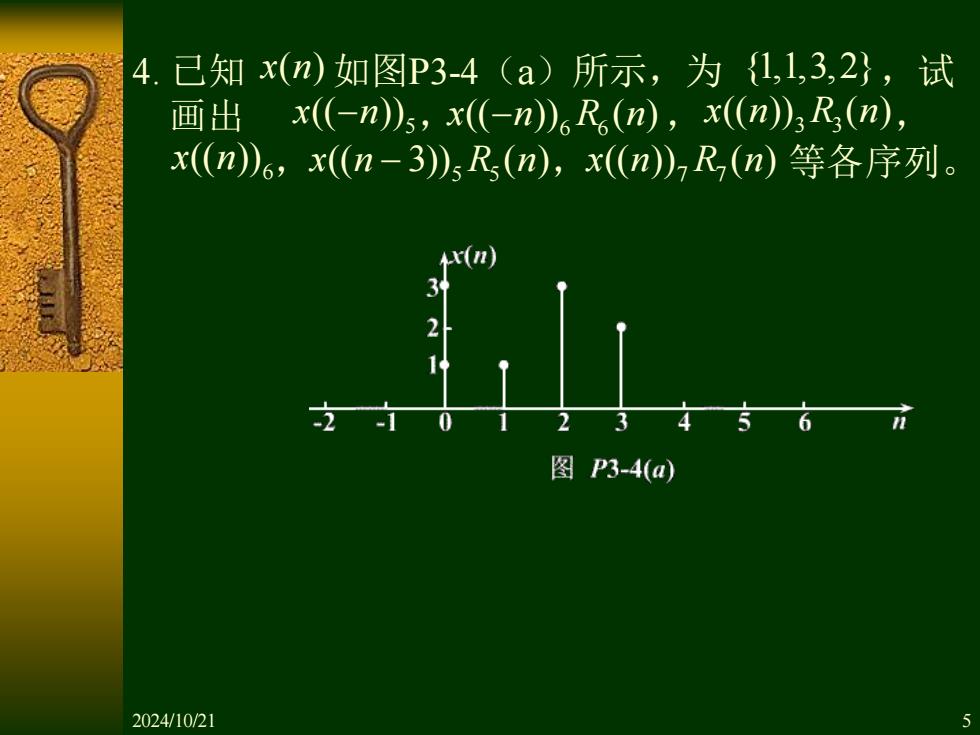
4. 已知x(n)如图P3-4(a)所示,为{1,1,3,2},试 画出x(-n)5,x(-n)6R,(n),x(n)3R(n), x(n)6,x(n-3)sR(n),x(n),R(n)等各序列。 (n 图P3-4(a) 2024/10/21
4. 已知 如图P3-4(a)所示,为 ,试 画出 , , , , , 等各序列。 x n( ) {1,1,3,2} 5 x n (( )) − 6 6 x n R n (( )) ( ) − 3 3 x n R n (( )) ( ) 6 x n (( )) 5 5 x n R n (( 3)) ( ) − 7 7 x n R n (( )) ( ) 2024/10/21 5
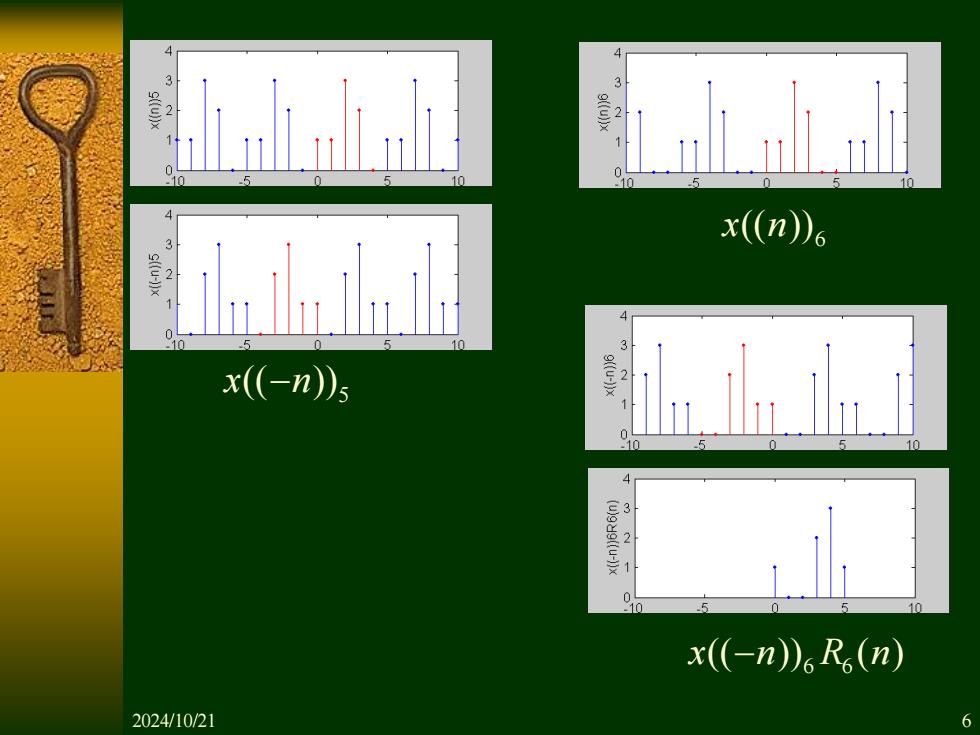
4 3 小 0 x(n)。 Irir w s 3 x(-n)5 32 10 x(-n)6R(n) 2024/10/21 6
5 x n (( )) − 6 x n (( ))6 6 x n R n (( )) ( ) − 2024/10/21 6

32 l h s((e-u)x x((n)):R(n) 3 2 1 7 09 x(n-3)5R(n) 4 2 2024/10/21 x(n)2R,(n)
5 5 x n R n (( 3)) ( ) − 3 3 x n R n (( )) ( ) 7 7 x n R n (( )) ( ) 2024/10/21 7

5.试求以下有限长序列的N点DFT(闭合形式表 达式): (1)x(n)=acos(@on)R(n) N-1 解:X(k)=∑x(n)WRv(k) n=0 .sag分元因 n=0 =。为k 2024/10/21
5. 试求以下有限长序列的 点 (闭合形式表 达式): N DFT 0 ( ) cos( ) ( ) N (1) x n a n R n = 1 0 ( ) ( ) ( ) N nk N N n X k x n W R k − = 解: = 0 0 1 2 0 1 ( ) ( ) 2 N j nk j n j n N N n a e e e R k − − − = = + 1 2 0 0 cos( ) ( ) N j nk N N n a n e R k − − = = 0 0 1 1 2 2 ( ) ( ) 0 0 1 ( ) 2 N N j k n j k n N N N n n a e e R k − − − + − − = = = + 2024/10/21 8

1-e-jooN 1-e-jooN a 2元k+0) 1-e Ry(k) 2 -j 1-e @oN 2 -e 2 -0N 2 e e 2 eew-e 2 Ry(k) sin() 2 Ry(k) sin(k+o,) sin( 2 2024/10/21
0 0 0 0 2 2 ( ) ( ) 1 1 1 ( ) 2 1 1 j N j N N j k j k N N e e a R k e e − − − + − − − − = + − − 0 0 0 0 0 0 2 2 2 1 2 1 2 1 2 ( ) ( ) ( ) 2 2 2 1 ( ) 2 ( ) N N N j j j j k j k j k N N N e e e a e e e − − − + + − + − = − 0 0 0 0 0 0 2 2 2 1 2 1 2 1 2 ( ) ( ) ( ) 2 2 2 ( ) ( ) ( ) N N N j j j N j k j k j k N N N e e e R k e e e − − − − − − − − − − 0 0 0 0 1 1 2 2 0 0 sin( ) sin( ) 1 2 2 ( ) 2 1 1 sin( ) sin( ) 2 2 N N j k j j k j N N N N N a e e R k k k N N − − − + = − + − 2024/10/21 9

(2)x(n)=a”Rv(n) 解:X内)-2ogR,内 n=0 Ry(k) n=0 -Ry(k) 1-ae -k 2024/10/21 10
1 2 0 ( ) N j nk n N N n a e R k − − = = (2) ( ) ( ) n N x n a R n = 1 0 ( ) ( ) ( ) N nk N N n X k x n W R k − = 解: = 2 1 ( ) 1 N N j k N a R k ae − − = − 1 2 0 ( ) n N j k N N n ae R k − − = = 2024/10/21 10