
第五章习题讲解 2024/10/21
第五章习题讲解 2024/10/21 1

用直接I型及典范结构实现以下系统函数: 3+4.2z1+0.8z2 2+0.6z1-0.422 解:根据IIR滤波器的系统函数标准式 M H(2=-=0 Y(2) x( n= 将系统函数整理为: H(a) 1.5+2.1z1+0.4z21.5+2.1z1+0.4z2 1+0.3z1-0.2z21-(-0.3z1+0.2z2) 2024/10/21
1、用直接I型及典范结构实现以下系统函数: ( ) 1 2 1 2 3 4.2 0.8 2 0.6 0.4 z z H z z z − − − − + + + − = 解:根据IIR滤波器的系统函数标准式 ( ) 1 2 1 2 1.5 2.1 0.4 1 0.3 0.2 z z H z z z − − − − + + + − = 将系统函数整理为: ( ) ( ) ( ) 0 1 1 M m m m N n n n b z Y z H z X z a z − = − = = − = ( ) 1 2 1 2 1.5 2.1 0.4 1 0.3 0.2 z z z z − − − − + + = − − + 2024/10/21 2

H(a)= 1.5+2.1z1+0.4z2 -(-0.3z+02z2) 得a1=-0.3,42=0.2b=1.5,b=2.1,b2=0.4 x(n) 1.5 y(n) 直接I型结构: 2.1 -0.3 0.4 0.2 图P5-1(a 典范型结构: x(n) 1.5 v(n) -0.3 2. 0.2 0.4 2024/10/21 3
1 a = −0.3 2 得 , a = 0.2 0 b =1.5 1 b = 2.1 2 , , b = 0.4 直接I型结构: 典范型结构: ( ) 1 2 1 2 1.5 2.1 0.4 ( ) 1 0.3 0.2 z z H z z z − − − − + + = − − + 2024/10/21 3

2、用级联型结构实现以下系统函数: H( 4(2+10(2-1.4z+1) (z-0.5)(z2+0.9z+0.8) 试问一共能构成几种级联型网络。 保门 41+z)(1-14z+z2) (1-0.5z)1+0.9z+0.8z2) 则A=4 B,=1 B2,=0 B2=-14B2=1 202410%1=0.5 021=0 012=-0.922=-0.8
解: ( )( ) ( )( ) 1 1 2 1 1 2 4 1 1 1.4 1 0.5 1 0.9 0.8 z z z z z z − − − − − − + − + = − + + ( ) 1 2 1 2 1 2 1 2 1 1 k k k k k z z H z A z z − − − − + + = − − 11 =1 21 = 0 11 = 0.5 21 = 0 12 = −1.4 22 =1 22 = −0.8 12 = −0.9 则 A = 4 2、用级联型结构实现以下系统函数: ( ) ( )( ) ( )( ) 2 2 4 1 1.4 1 0.5 0.9 0.8 z z z H z z z z + − + − + + = 试问一共能构成几种级联型网络。 2024/10/21 4
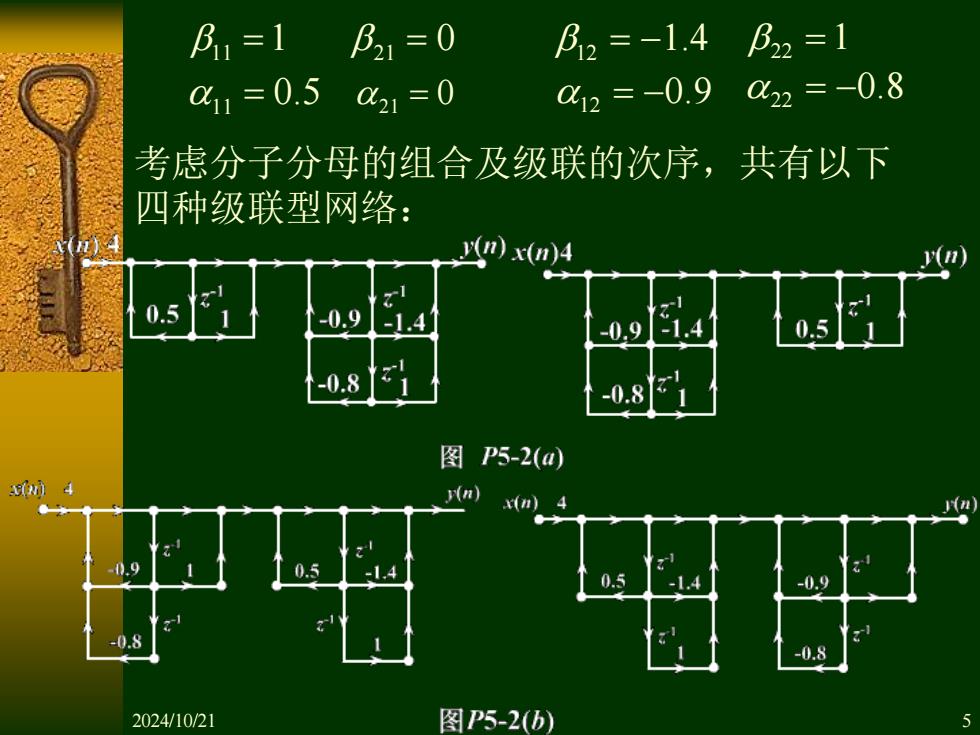
B,=1 B21=0 B2=-1.4阝2=1 C1=0.5 021=0 c12=-0.9022=-0.8 考虑分子分母的组合及级联的次序,共有以下 四种级联型网络: y(n)x(n)4 0.5 -0.9 -0.9 1.4 0.5 -0.8 -0.8 图P5-2(a0 0.9 0.5 -0.9 -0.8 -0.8 2024/10/21 图P5-2(b) 5
考虑分子分母的组合及级联的次序,共有以下 四种级联型网络: 11 =1 21 = 0 11 = 0.5 21 = 0 12 = −1.4 22 =1 22 = −0.8 12 = −0.9 2024/10/21 5

3、给出以下系统函数的并联型实现: # 5.2+1.58z1+1.41z2-1.6z3 1-0.5z)1+0.9z+0.8z 解:对此函数进行因式分解并展成部分分式,得 H日 5.2+1.58z1+1.41z2-1.6z-3 (1-0.5z)1+0.9z1+0.8z2) 0.2 1+0.3z1 =4+ 1-0.5zT1+0.9z1+0.822 0+会子2 [N+H)/2] 则G。=4 1-a2-a C1=0.5 C21=0 a2=-0.9a2=-0.8 =0.2 Y,=0 Yo2=1 72=0.3
3、给出以下系统函数的并联型实现: ( ) ( )( ) 1 2 3 1 1 2 5.2 1.58 1.41 1.6 1 0.5 1 0.9 0.8 z z z H z z z z − − − − − − + + − − + + = 解:对此函数进行因式分解并展成部分分式,得 ( ) ( )( ) 1 2 3 1 1 2 5.2 1.58 1.41 1.6 1 0.5 1 0.9 0.8 z z z H z z z z − − − − − − + + − = − + + 1 1 1 2 0.2 1 0.3 4 1 0.5 1 0.9 0.8 z z z z − − − − + = + + − + + 则 0 G = 4 11 = 0.5 21 = 0 01 = 0.2 11 = 0 12 = −0.9 22 = −0.8 02 =1 12 = 0.3 ( ) ( 1 / 2 ) 1 0 1 0 1 2 1 1 2 1 N k k k k k z H z G z z + − − − = + = + − − 2024/10/21 6
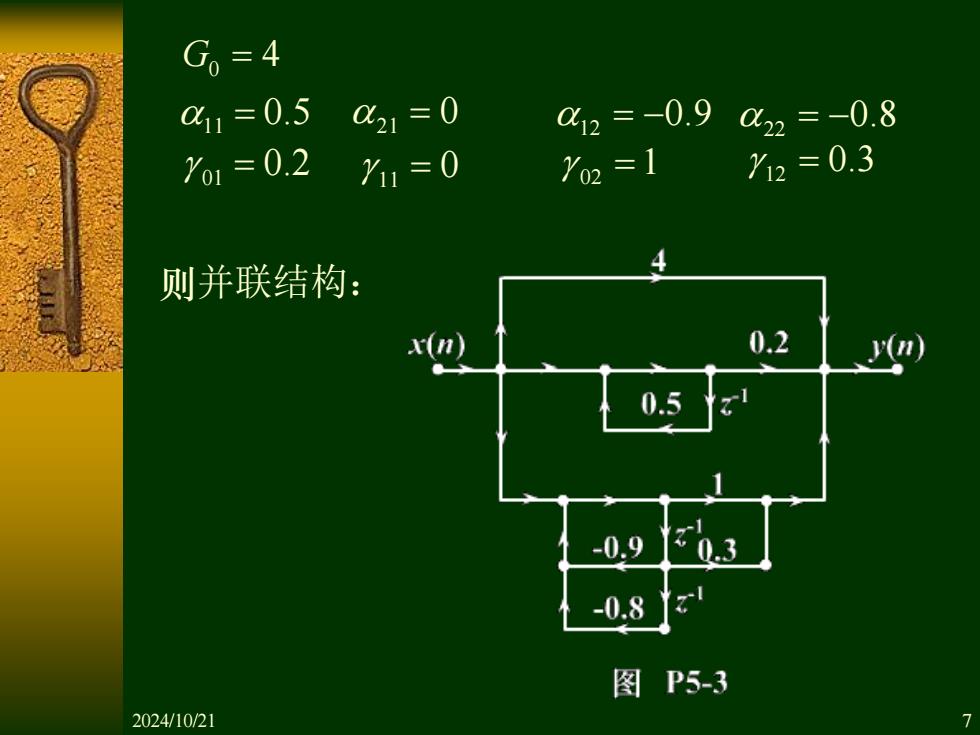
G=4 Cx11=0.5 C21=0 c2=-0.9x2=-0.8 Yo1=0.2711=0 Y2=1 Y12=0.3 则并联结构: x(n) 0.2 0.5 -0.9 0.3 -0.8 图P5-3 2024/10/21
则并联结构: 0 G = 4 11 = 0.5 21 = 0 01 = 0.2 11 = 0 12 = −0.9 22 = −0.8 02 =1 12 = 0.3 2024/10/21 7

1、用横截型结构实现以下系统函数: y0-j0+s0-20-。0- e-0+6:0-2=+&-) -201+6+6g+j0- 20-) =1+1- 8 205 3 2+205 12 一之 2024/10/21 6
4、用横截型结构实现以下系统函数: ( ) ( )( ) ( ) 1 1 1 1 1 1 1 1 1 6 1 2 1 1 2 6 H z z z z z z − − − − − − + − + − = 解: ( ) ( )( ) ( ) 1 1 1 1 1 1 1 1 1 6 1 2 1 1 2 6 H z z z z z z − − − − − − + − + − = ( ) 1 1 1 1 2 1 1 2 1 1 2 1 6 1 2 6 z z z z z z z − − − − − − − − − + + + + − = ( ) 5 37 1 2 1 2 1 1 1 1 2 6 z z z z z − − − − − − + + + − = 8 205 205 8 1 2 3 4 5 1 3 12 12 3 z z z z z − − − − − = + − + − − 2024/10/21 8
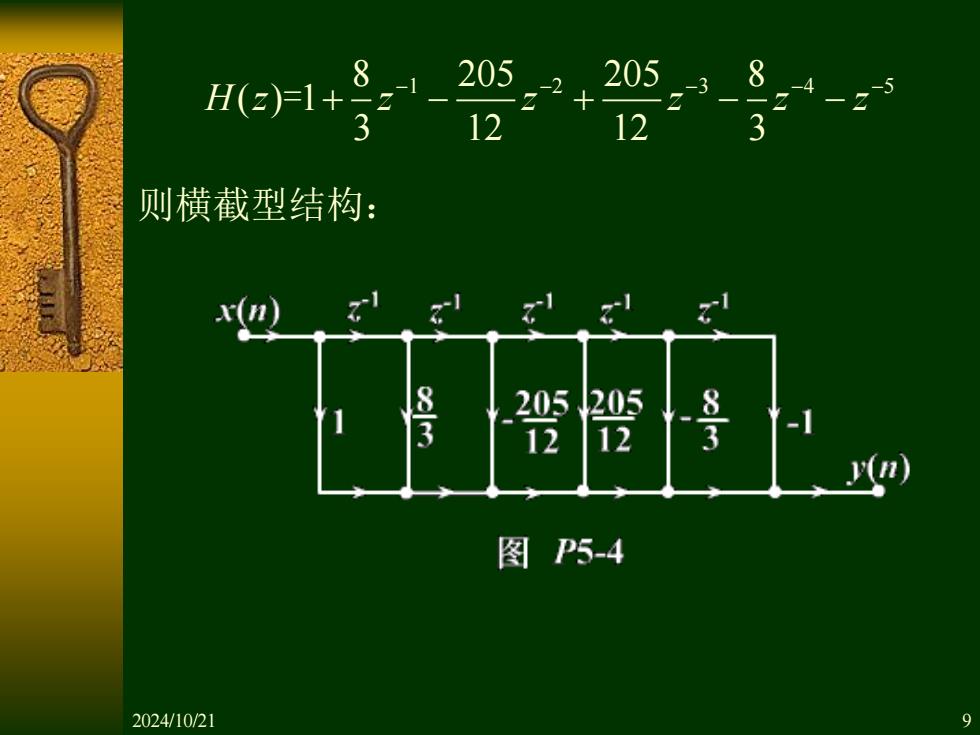
8.-1205 He少1+32 22+ 205 3 8 12 12 则横截型结构: z1 8-3 .205205 12 12 -1 图P5-4 2024/10/21 9
则横截型结构: 8 205 205 8 1 2 3 4 5 ( ) 1 3 12 12 3 H z z z z z z − − − − − = + − + − − 2024/10/21 9

6、用频率抽样结构实现以下系统函数: H(e)=5-2:3-3z 1-z1 抽样点数N=6,修正半径r=0.9。 解:由N=6,得频率抽样型结构: 4-日同 25100-:0: 1-2 =(5+3z01+z'+z2) 2024/10/21 10
6、用频率抽样结构实现以下系统函数: ( ) 3 6 1 5 2 3 1 z z H z z − − − − − − = 抽样点数 N = 6 ,修正半径 r = 0.9 。 解:由N = 6,得频率抽样型结构: ( ) ( ) ( ) ( ) ( ) 2 6 6 0 3 1 1 1 6 k k H z r z H z H z H z − = − + + = ( )( ) 3 1 2 5 3 1 z z z − − − = + + + ( )( ) 1 1 2 1 1 z z z → − + + − − − ( ) ( )( ) 3 3 1 5 3 1 1 z z H z z − − − + − − = 又 2024/10/21 10