
第六章习题讲解 2024/10/21
第六章习题讲解 2024/10/21 1

用冲激响应不变法将以下H(s)变换为H(), 抽样周期为T。 1)H.)=(s+a/[s+a+6] 解:冲激响应不变法: 1,)=之4 s- TA 将H,(s部分分式分解: H.(s)= s+a (sta)2+b2 "s+a-jb 2024/10/21
解:冲激响应不变法: 1.用冲激响应不变法将以下 变换为 抽样周期为T。 H s a ( ) H z( ) , (1) ( ) ( ) ( ) 2 2 H s s a s a b a = + + + ( ) ( ) 2 2 a s a H s s a b + = + + 1 ( ) N k a k k A H s = s s = − 1 1 ( ) 1 k N k s T k TA H z e z − = = − 1 1 1 2 s a jb s a jb = + + + + − 将 H s a ( ) 部分分式分解: 2024/10/21 2

经冲激响应不变法变换后得: T -71-26oe 1-e-aT=cos(bT) 2024/10/21
经冲激响应不变法变换后得: ( ) ( ) 1 1 2 2 1 cos 1 2 cos aT aT aT e z bT T e z bT e z − − − − − − − = − + ( ) 1 1 1 2 H s a s a jb s a jb = + + + + − ( ) 1 1 ( ) 1 ( ) 2 1 1 a jb T a jb T T T H z e z e z − + − − − − = + − − 2024/10/21 3

设有一模拟滤波器 H.()=(s2+s+1) 抽样周期T=2,试用双线性变换法将它转变 为数字系统函数H(②) 解:由变换公式s=c 1-z1 1+2 及c-子7-2可袋司 1+2 H阳间=(s以篇 3+z2 2024/10/21
3.设有一模拟滤波器 抽样周期 ,试用双线性变换法将它转变 为数字系统函数 ( ) ( ) 2 1 1 H s s s a = + + T = 2 H z( ) 解:由变换公式 1 1 1 1 z s c z − − − = + 及 2 c T = , T = 2 ,可得 1 1 1 1 z s z − − − = + ( ) ( ) 1 1 1 1 z a s z H z H s − − − = + = 2 1 1 1 1 1 1 1 1 1 1 z z z z − − − − = − − + + + + ( ) 2 1 2 1 3 z z − − + = + 2024/10/21 4

4.要求从二阶巴特沃思模拟滤波器用双线性变换 导出一低通数字滤波器,已知3dB截止频率为 100Hz,系统抽样频率为1kHz。 解:归一化的二阶巴特沃思滤波器的系统函数为: 1 1 H.()-+2s+i3+14142136s+1 则将s=s/2.代入,得出截止频率为2.(100×2π) 的模拟原型为 H(s)= S +1.4142136 +1 200元 200元 394784.18 s2+888.58s+394784.18 2024/10/21 5
4.要求从二阶巴特沃思模拟滤波器用双线性变换 导出一低通数字滤波器,已知3dB截止频率为 100Hz,系统抽样频率为1kHz。 解:归一化的二阶巴特沃思滤波器的系统函数为: ( ) 2 2 1 1 2 1 1.4142136 1 H s a s s s s = = + + + + 则将 s s = c 代入,得出截止频率为 c (100 2 ) 的模拟原型为 ( ) 2 1 1.4142136 1 200 200 H s a s s = + + 2 394784.18 s s 888.58 394784.18 = + + 2024/10/21 5

394784.18 H,()=2+88858s+394784.18 经双线性变换得数字滤波器的系统函数: e)=H.(s以 T=1/f=1/103(s) 394784.18 +394784.18 0.064(1+2z1+z2) 1-1.1683z1+0.4241z2 2024/10/21
经双线性变换得数字滤波器的系统函数: ( ) ( ) 1 1 2 1 1 a z s T z H z H s − − − = + = 2 1 1 3 3 1 1 394784.18 1 1 2 10 888.58 2 10 394784.18 1 1 z z z z − − − − = − − + + + + ( ) 1 2 1 2 0.064 1 2 1 1.1683 0.4241 z z z z − − − − + + = − + 3 1/ 1/10 ( ) T f s = = s ( ) 2 394784.18 888.58 394784.18 H s a s s = + + 2024/10/21 6

5.试导出二阶巴特沃思低通滤波器的系统函数。 设2.=3rad/s 南eY方数:Ua时:,心 令22=-s2,则有 H日(7 各极点满足下式 4=2e传4 k=1,2,3,4 2024/10/21 7
5.试导出二阶巴特沃思低通滤波器的系统函数。 设 3 c = rad s 解:由幅度平方函数: ( ) ( ) 2 4 1 1 c H j = + 令 2 2 = −s ,则有 ( ) ( ) ( ) 4 1 1 a a c H s H s s − = + 各极点满足下式 2 1 2 4 k j k c s e − + = k =1 2 3 4 , 2024/10/21 7

则k=1,2时,所得的s即为H(s)的极点 =0e-32+32 2 -2e-33 2 由以上两个极点构成的系统函数为 ko k H.(⊙)6-ss-s)y+32s+9 代入s=0时H(s)=1,可得K,=9,所以 9 H.(9)-+32s+9 2024/10/21 8
则 k =1,2 时,所得的 sk 即为 H s a ( ) 的极点 3 4 1 3 2 3 2 2 2 j c s e j = = − + 4 5 2 3 2 3 2 2 2 j c s e j = = − − 由以上两个极点构成的系统函数为 ( ) ( )( ) 0 0 2 1 2 3 2 9 a k k H s s s s s s s = = − − + + ( ) 1 代入 s = 0 时 H s a = ,可得 0 K = 9 ,所以 ( ) 2 9 3 2 9 H s a s s = + + 2024/10/21 8

6.试导出二阶切贝雪夫低通滤波器的系统函数。 已知通带波纹为2dB,截止频率为2.=2rad/s (试用不同于书本的解法解答)。 解:由6=2dB,得 s2=100-1=1002-1=0.5848932 则8=√0.5848932=0.7647831 因为截止频率为2。=2rad/s,则 2024/10/21 9
6.试导出二阶切贝雪夫低通滤波器的系统函数。 已知通带波纹为2dB,截止频率为 (试用不同于书本的解法解答)。 2 c = rad s 解:由 1 = 2dB ,得 1 2 0.2 10 10 1 10 1 0.5848932 = − = − = 则 = = 0.5848932 0.7647831 因为截止频率为 2 c = rad s ,则 2024/10/21 9
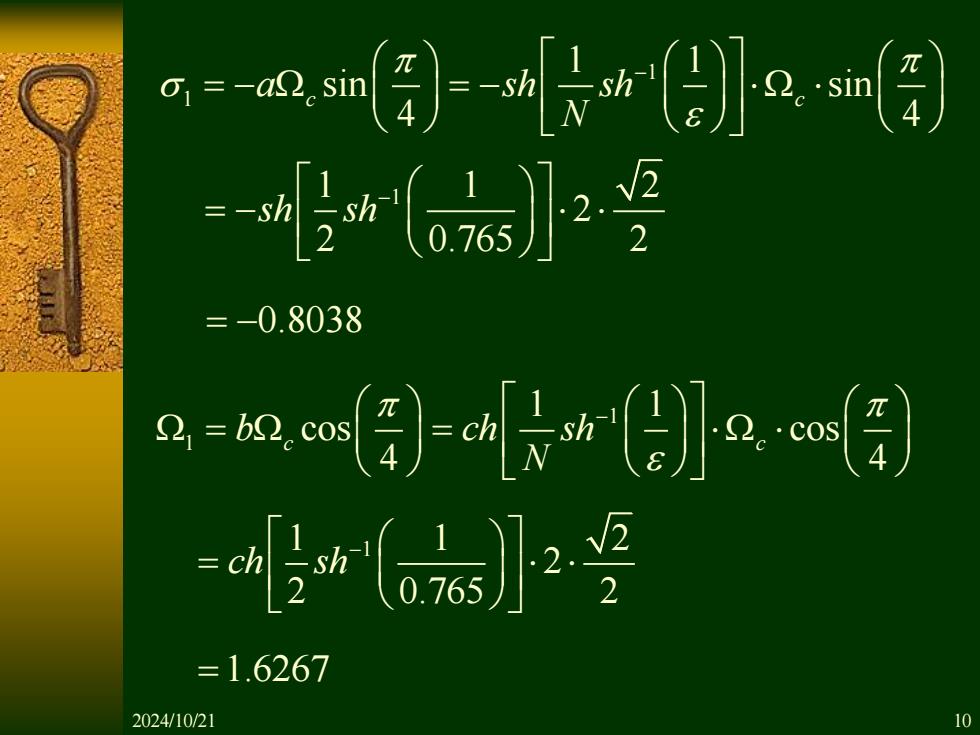
mn-nn写到 -06s =-0.8038 n=am日w)no目 小:9 =1.6267 2024/10/21 10
1 1 1 1 sin sin 4 4 c c a sh sh N − = − = − 1 1 2 1 2 2 0.765 2 sh sh − = − = −0.8038 1 1 1 1 cos cos 4 4 c c b ch sh N − = = 1 1 2 1 2 2 0.765 2 ch sh − = =1.6267 2024/10/21 10