
第七章习题讲解 2024/10/21
第七章习题讲解 2024/10/21 1

用矩形窗设计一个FIR线性相位低通数字滤波器。 已知0.=0.5π,N=21。求出h(n并画出 20lgH(e曲线。 线性相位理想低通滤波器 e-jwa -0。≤0≤0。 0 -π≤0≤-0,0。≤0≤元 其单位抽样响应: a)-27,(e)edo ewge o(n-) 2024/10/21
解:线性相位理想低通滤波器 1.用矩形窗设计一个FIR线性相位低通数字滤波器。 已知 , 。求出 并画出 曲线。 c=0.5 N = 21 h n( ) 20lg ( ) j H e 其单位抽样响应: ( ) ( ) 1 2 j j n h n H e e d d d − = ( ) 0 , j j c c d c c e H e − − = − − ( ) ( ) sin c c c n n − = − 1 2 c c j j n e e d − − = 2024/10/21 2

h(n)=2.sin[a.(u-a)] π Q.(n-a) 其中=1=10 0。=0.5π 2 用矩形窗截断得FIR滤波器: nπ -sin 2 na)=h,(nw(m)=rn-1 0≤n≤20 0 n其他 其中w(n)=,(n)是窗函数。 2024/10/21 3
其中 1 10 2 N − = = 0.5 c = 用矩形窗截断得FIR滤波器: ( ) ( ) ( ) ( ) sin 2 , 0 20 10 0 d n h n h n w n n n n − = = − 其他 其中 w n R n ( ) = 21 ( )是窗函数。 ( ) ( ) ( ) sin c c d c n h n n − = − 2024/10/21 3
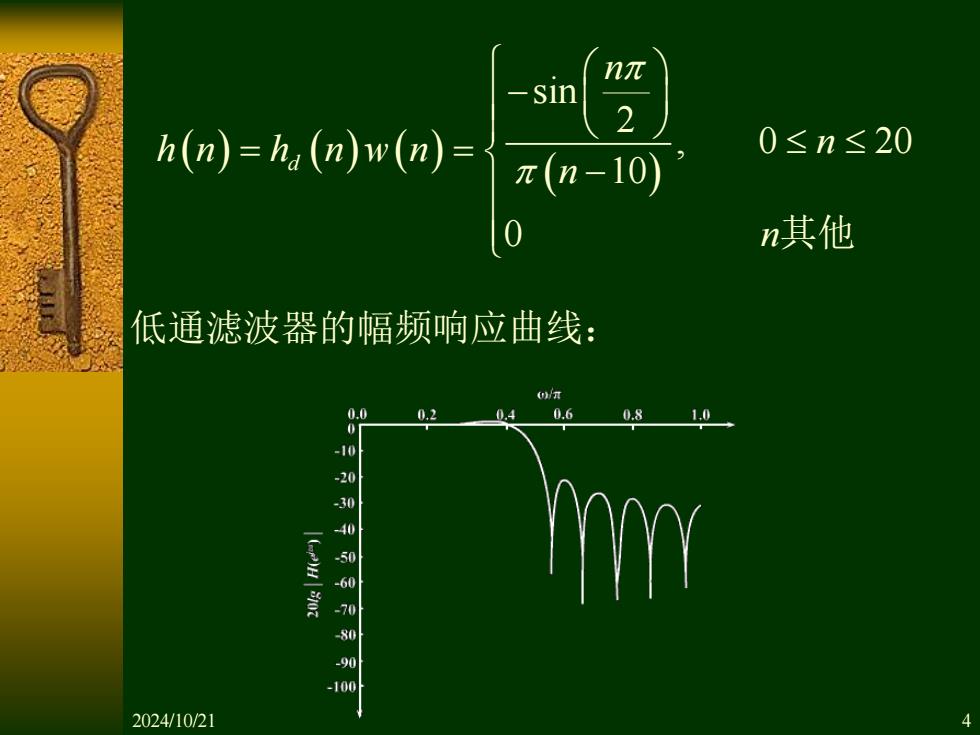
nπ -sin \2 h(m=,(nw()=π(n-1o) 0≤n≤20 n其他 低通滤波器的幅频响应曲线: / 0.6 0. 2024/10/21
低通滤波器的幅频响应曲线: ( ) ( ) ( ) ( ) sin 2 , 0 20 10 0 d n h n h n w n n n n − = = − 其他 2024/10/21 4

?.试用频率抽样法设计一个FIR线性相位数字低通 滤波器,已知0。=0.5π,N=51。 取不超车以.ey日 0≤0≤0。 其它o 第一种频率抽样,得 1,03ksInt =12 08 H)= 06 0, 13sks N-1 04 =25 0.2 2 10 1520 25 则FIR滤波器的频率响应: 51 kπ 0kπ sin 51 sin 51 H(e)=e2sa 2 2 51 2 51 kπ 51sin k=1 51sin 0 kπ 55sin 2 2 51 2 51 2024/10/21
则FIR滤波器的频率响应: 7.试用频率抽样法设计一个FIR线性相位数字低通 滤波器,已知 c = 0.5 , N = 51 。 解:根据题意有 ( ) 1 0 0 j c H e d = 其它 按第一种频率抽样,得 ( ) 1, 0 12 2 1 0, 13 25 2 N c k Int H k N k = = − = ( ) 12 25 1 51 sin sin 51 sin 51 2 2 51 2 51 51sin 51sin 55sin 2 2 51 2 51 j j k k k H e e k k − = − + = + + − + 2024/10/21 5

按第二种频率抽样,得 )= 0, 1-25 13sk≤N 08 04 则FIR滤波器的频率响应: 02 0 10 202 25 sin51 ")e 2 51sin 0 2024/10/21 6
则FIR滤波器的频率响应: 按第二种频率抽样,得 ( ) 1, 0 12 2 1 0, 13 25 2 c N k Int N H k N k − = = − = ( ) 12 25 0 1 1 sin 51 sin 51 2 51 2 2 51 2 1 1 51sin 51sin 2 51 2 2 51 2 j j k k k H e e k k − = − + + + = + − + + + 2024/10/21 6
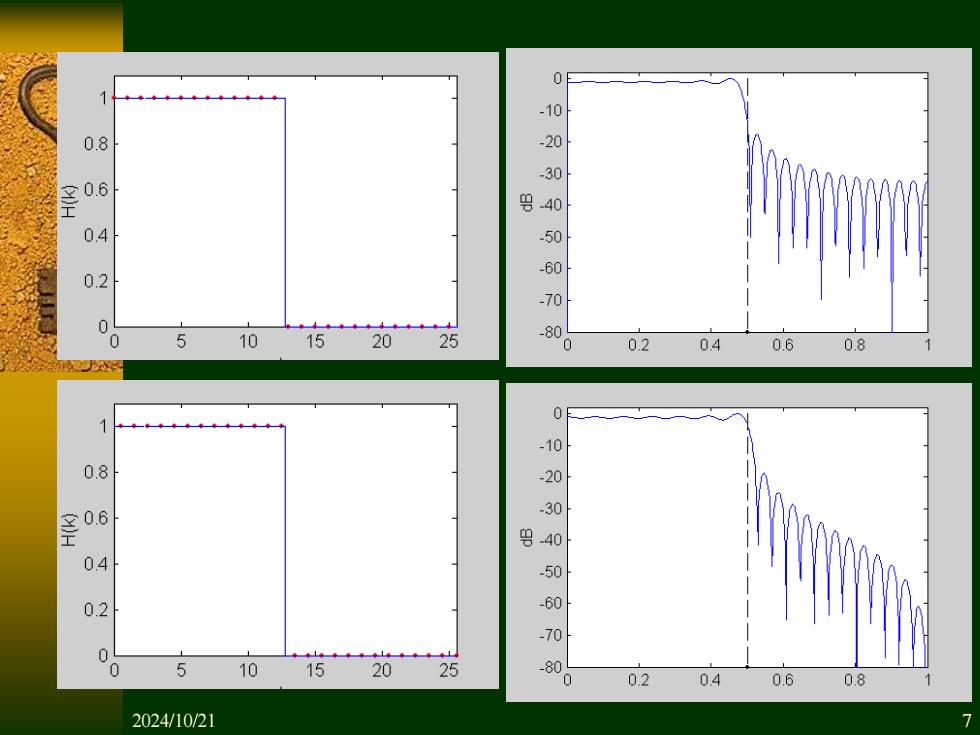
0 08 0.6 0.4 11000000 0.2 0 5 10152025 0 0.2 040.6 0.8 7 08 1000 夕 0.4 0.2 1 0 5 10 15 20 25 0 0.2 04 0.6 08 2024/10/21
2024/10/21 7
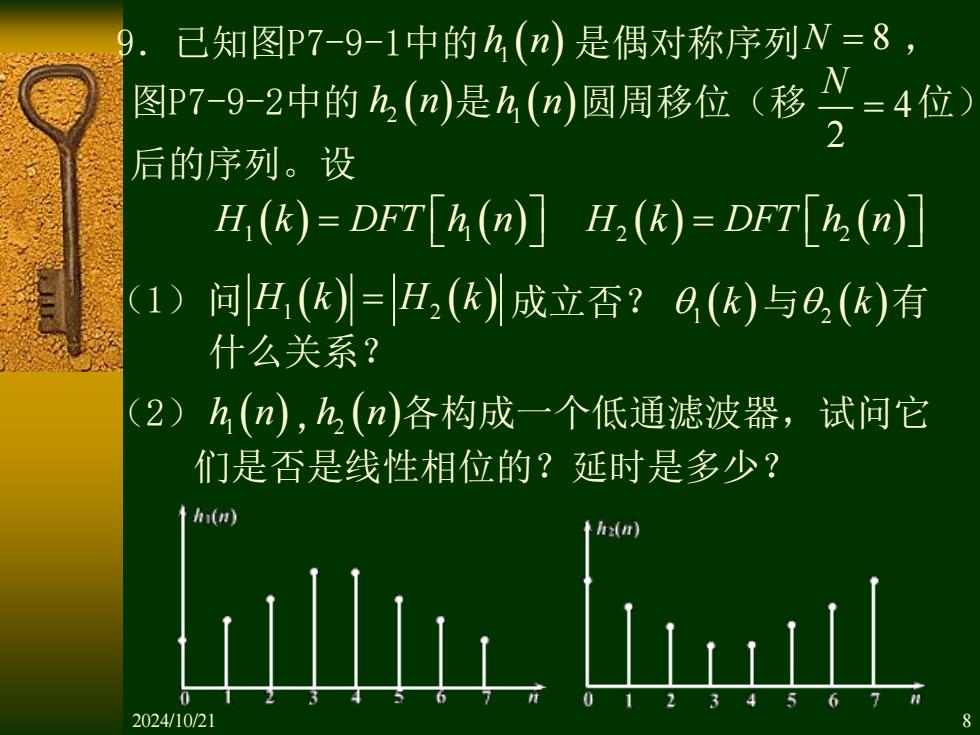
已知图P7-9-1中的h(n)是偶对称序列N=8, 图P7-9-2中的h(n)是h(n)圆周移位 (移=4位) 2 后的序列。设 H(k)=DFT[h(n)]H.(k)=DFT[h(n)] 1) 问H,(k=H,(成立否?Q(k)与O,(k)有 什么关系? (2)h(n),h2(n)各构成一个低通滤波器,试问它 们是否是线性相位的?延时是多少? h(n) 2024/10/21
9.已知图P7-9-1中的 是偶对称序列 , 圆周移位(移 位) h n 1 ( ) N = 8 图P7-9-2中的 h n 2 ( ) 是 h n 1 ( ) 4 2 N = 后的序列。设 H k DFT h n 1 1 ( ) = ( ) H k DFT h n 2 2 ( ) = ( ) (1)问 H k H k 1 2 ( ) = ( ) 成立否? 1 (k ) 与 2 (k ) 有 什么关系? (2) h n 1 ( ) , h n 2 ( ) 各构成一个低通滤波器,试问它 们是否是线性相位的?延时是多少? 2024/10/21 8

(1)根据题意可知 b()=h(-4 则 H,(=∑a(a-4WgR(o 2A(w=g“∑AW =H(k)Ws 由上式可以看出 H()=H,(k g个)=2(因铁=9)-知 2024/10/21 9
解:(1)根据题意可知 2 1 (( )) (( )) 8 8 h n h n = − 4 则 ( ) 4 3 4 1 8 8 4 i n ki k i h i W W = − = − = ( ) (( )) ( ) 7 2 1 8 8 8 0 4 nk n H k h n W R n = = − ( ) 4 1 8 k = H k W 由上式可以看出 H k H k 2 1 ( ) = ( ) 2 1 1 ( ) ( ) ( ) 2 4 8 k k k k k = − = − ( ) 7 4 8 1 8 0 k ki i W h i W = = 2024/10/21 9

2)h(n,h,(n)各构成低通滤波器时, 由于都满足偶对称,因此都是线性相位的。 延时为 a- N-17 =3.5 22 2024/10/21 10
(2) h n 1 ( ) , h n 2 ( ) 各构成低通滤波器时, 由于都满足偶对称,因此都是线性相位的。 1 7 3.5 2 2 N − = = = 延时为 2024/10/21 10