
电子技术基础模拟部分 第五版 9信号处理与信号产生电路 9.1滤波电路的基本概念与分类 9.1.1在下列几种情况下,应分别采用哪种类型的滤波电路(低通、高 通、带通、带阻)?(1)有用信号频率为100Hz;(2)有用信号频率低于400Hz: (3)希望抑制50Hz交流电源的干扰;(4)希望抑制500Hz以下的信号。 解:(1)带通滤波电路;(2)低通滤波电路;(3)带阻滤波电路;(4)高通 滤波电路。 9.1.2设运放为理想器件。在下列几种情况下,试回答它们应分别属于 哪种类型的滤波电路(低通、高通、带通、带阻)?并定性画出其幅频特性。 (1)理想情况下,当f=0和f=∞时的电压增益相等,且不为零;(2)直流电 压增益就是它的通带电压增益;(3)在理想情况下,当f一∞时的电压增益就 是它的通带电压增益;(4)在f=0和一∞时,电压增益都等于零。 解:(1)带阻滤波电路;(2)低通滤波电路;(3)高通滤波电路;(4)带通 滤波电路。它们的幅频特性示意图分别如图解9.1.2a、b、c、d所示。 141 141 通带 (b) 通带 阻带 (d) 图解9.1.2
电子技术基础模拟部分 第五版
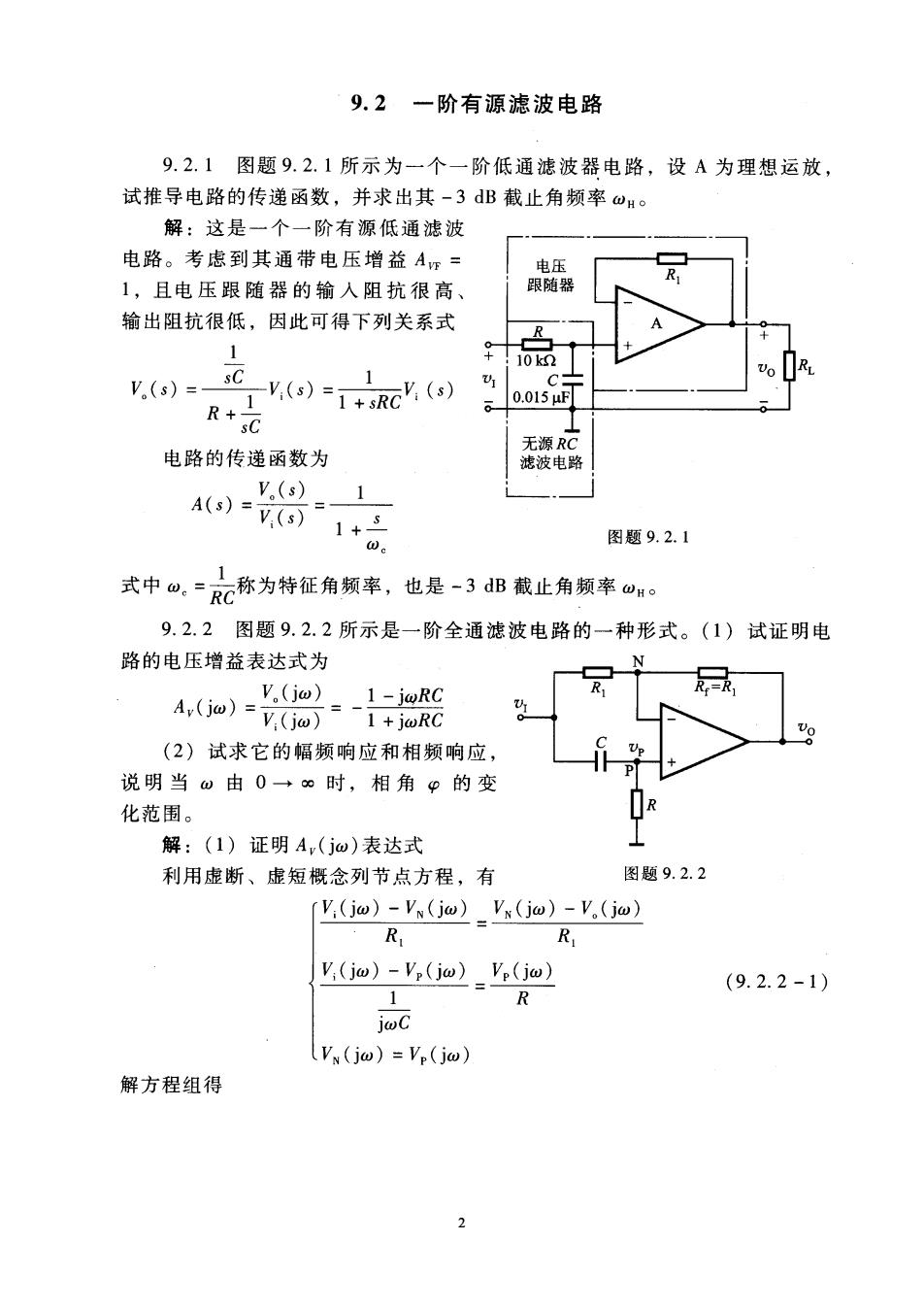
9.2一阶有源滤波电路 9.2.1图题9.2.1所示为一个一阶低通滤波器电路,设A为理想运放, 试推导电路的传递函数,并求出其-3dB截止角频率0H。 解:这是一个一阶有源低通滤波 电路。考虑到其通带电压增益Am= 1,且电压跟随器的输人阻抗很高 输出阻抗很低,因此可得下列关系式 R sC V.(s)= V,(o)=1+Rc() R+sC 电路的传递函数为 无源RC 滤波电路 A()-V() V(s) 1 1+ 图题9.2.1 式中a:=RC称为特征角频率,也是-3dB截止角频率“u。 9.2.2图题9.2.2所示是一阶全通滤波电路的一种形式。(1)试证明电 路的电压增益表达式为 A4(o)8-+e V(jw) 克 (2)试求它的幅频响应和相频响应, 说明当w由0→∞时,相角p的变 化范围。 R 解:(1)证明A,(jw)表达式 利用虚断、虚短概念列节点方程,有 图题9.2.2 [(jo)-V,(jm2_y,(jm)-V.(jo) R R V,(j)-V(jw)_V(j) (9.2.2-1) R joC Vx(jw)=Vp(jo) 解方程组得
2
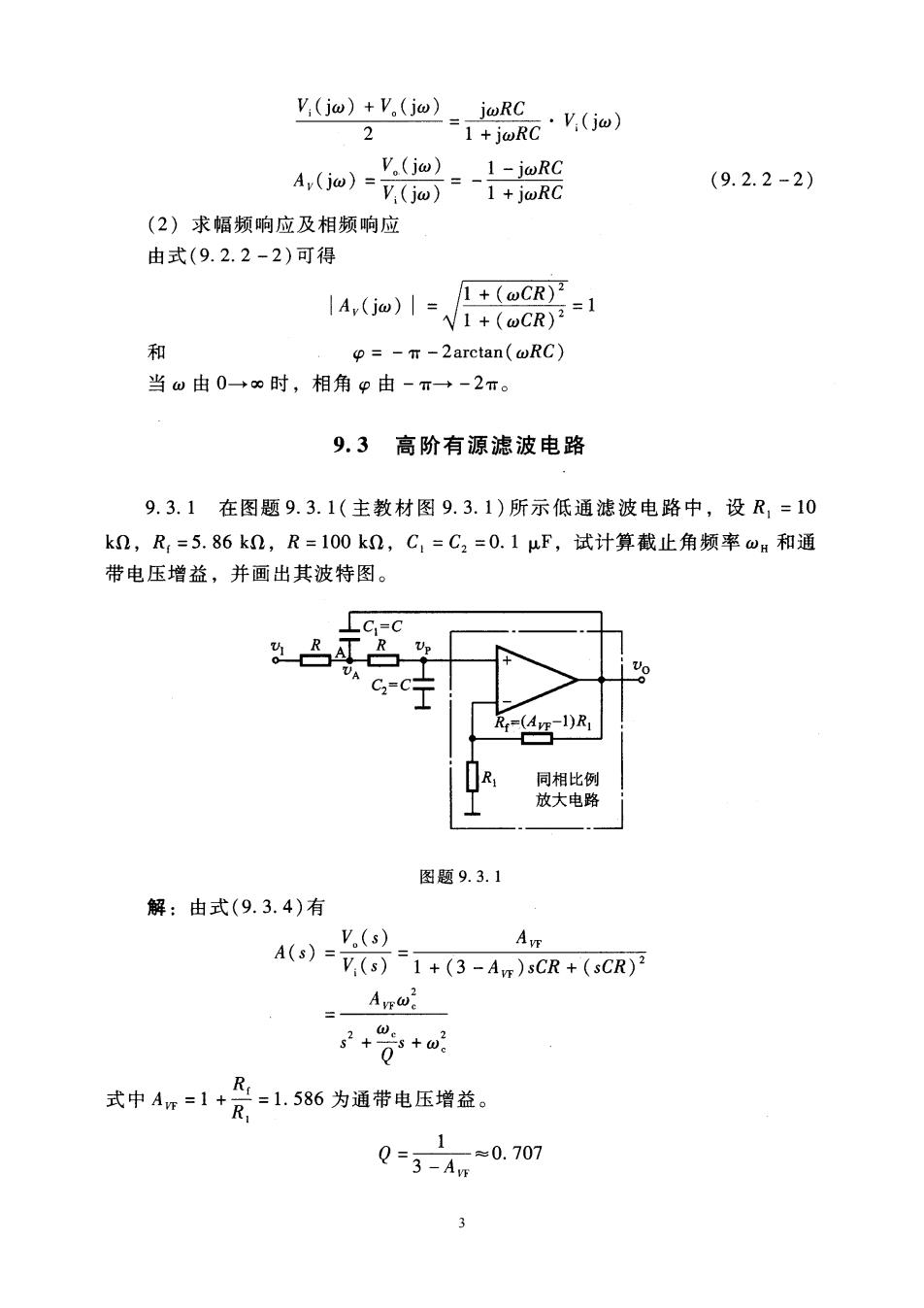
y.(jw)+v.(Go)=,joRc 2 1+jRc·上(ja) 08e A,(jo)=77o) (9.2.2-2) (2)求幅频响应及相频响应 由式(9.2.2-2)可得 |A(jw)|= 1+(CR) V1+(OCR)3=1 和 p=-T-2 arctan(wRC 当由0一0时,相角由-T→-2m。 9.3高阶有源滤波电路 9.3.1在图题9.3.1(主教材图9.3.1)所示低通滤波电路中,设R,=10 k,R,=5.86k,R=100k0,C,=C2=0.1uF,试计算截止角频率wa和通 带电压增益,并画出其波特图。 LC.=C Rr=(AvE-1)R1 同相比例 放大电路 图题9.3.1 解:由式(9.3.4)有 V.(s) A()=V(=1+(3-Aw)sCR+(CR) Ayrwe +0*w 式中4,=1+亮=1.586为通带电压增益。 1 Q-3-4*0.707 3
3
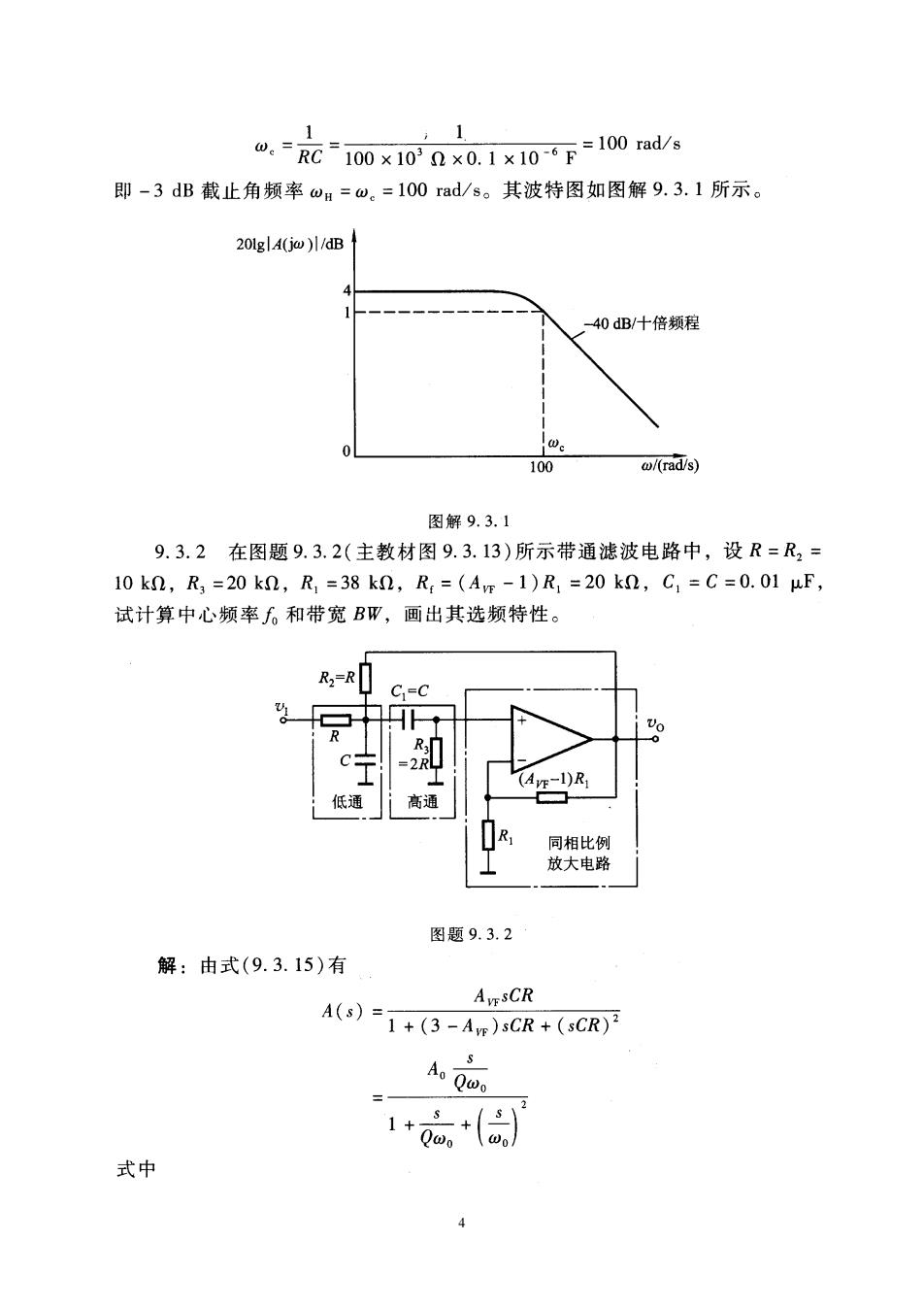
u.=c-100x10nx0.1x106F=100rads 即-3dB截止角频率wH=w。=100rad/s。其波特图如图解9.3.1所示。 201glA(j)/dB 40dB/十倍领程 100 w/(rad/s) 图解9.3.1 9.3.2在图题9.3.2(主教材图9.3.13)所示带通滤波电路中,设R=R2= 10k2,R,=20k2,R,=38k2,R=(Ap-1)R,=20k0,C1=C=0.01μF 试计算中心频率。和带宽BW,画出其选频特性。 R2=R C.EC 低通 高通 同相比例 放大电路 图题9.3.2 解:由式(9.3.15)有 AvsCR A()=1+(3-Am)CR+(SCR) 式中
4

4n1是1+0-1526 为同相比例放大电路的电压增益。 4=写久326=1.035 =c10×100x0.01×10F=10rad/s 称为中心角频率,品质因数 1 Q=3-A=0.678 由此可算出 87=20"2nX86s*2347k 104 和 人-2-1592 其选频特性示意图如图解9.3.2所示。 20g/dB 2-0.678 /(rad/s) BW- 图解9.3.2 9.3.3电路如图题9.3.3所示,设A1、A2为理想运放。(1)求A,(s)= 一及A智;2)根据导出的A,(和A)表达武,判渐它们分别 属于什么类型的滤波电路。 解:(1)求A(s)及A(s) V.(s) R sCR A()=(=-
5

图题9.3.3 A2组成反相求和电路,故有 V(s) .(s)=-V(s)-V()=1+CR 4o-得-1 (2)由A,(s)和A(s)可看出,A,组成一阶高通滤波电路,整个电路为一 阶低通滤波电路。 9.3.4设A为理想运放,试写出图题9.3.4所示电路的传递函数,指出 这是一个什么类型的滤波电路。 解:由图题9.3.4有 V.(s) R sCR -=-I+sCR 上式说明,这是一个一阶高通滤波电路。 图题9.3.4 图题9.3.5 9.3.5、设A为理想运放,试写出图题9.3.5所示电路的传递函数,指出 这是一个什么类型的滤波电路。 解:由图题9.3.5有
6

v()-(R) ()=0= .+C sC R -15CR,+GR+C,CR,R 上式说明,这是一个带通滤波电路。 9.3.6已知某有源滤波电路的传递函数为 v(s) 52 )=V(s)*RCRR02 1 (1)试定性分析该电路的滤波特性(低通、高通、带通或带阻)(提示:可从 增益随角频率变化情况判断);(2)求通带增益A。、特征角频率仙。及等效品 质因数Q。 解:(1)电路的滤波特性 令w。= ,原式可改写为 C√RR A(jw)) -1 (9.3.6-1) 1(总x R 对于上式,当a→0时,|A(j@)|→0;当0→∞时,A(j@)|→1。因 此,电路具有高通特性。 (2)求A,、w。及Q 由式(9.3.6-1)可知,A=-1,0.CRR0=31√/尼。 1 9.3.7高通电路如图题9.3.7(主教材图9.3.7)所示。已知Q=1,试求 其幅频响应的峰值,以及峰值所对应的角频率。设w。=2π×200rad/s。 解:此电路为压控电压源高通滤波器,其频率特性表达式为 A(j0)=-w2+jo.o70 Aw A(j@)=- 可 求表达式分母的最小值,可求得振幅达最大值所对应的角频率ω值 令 >
7
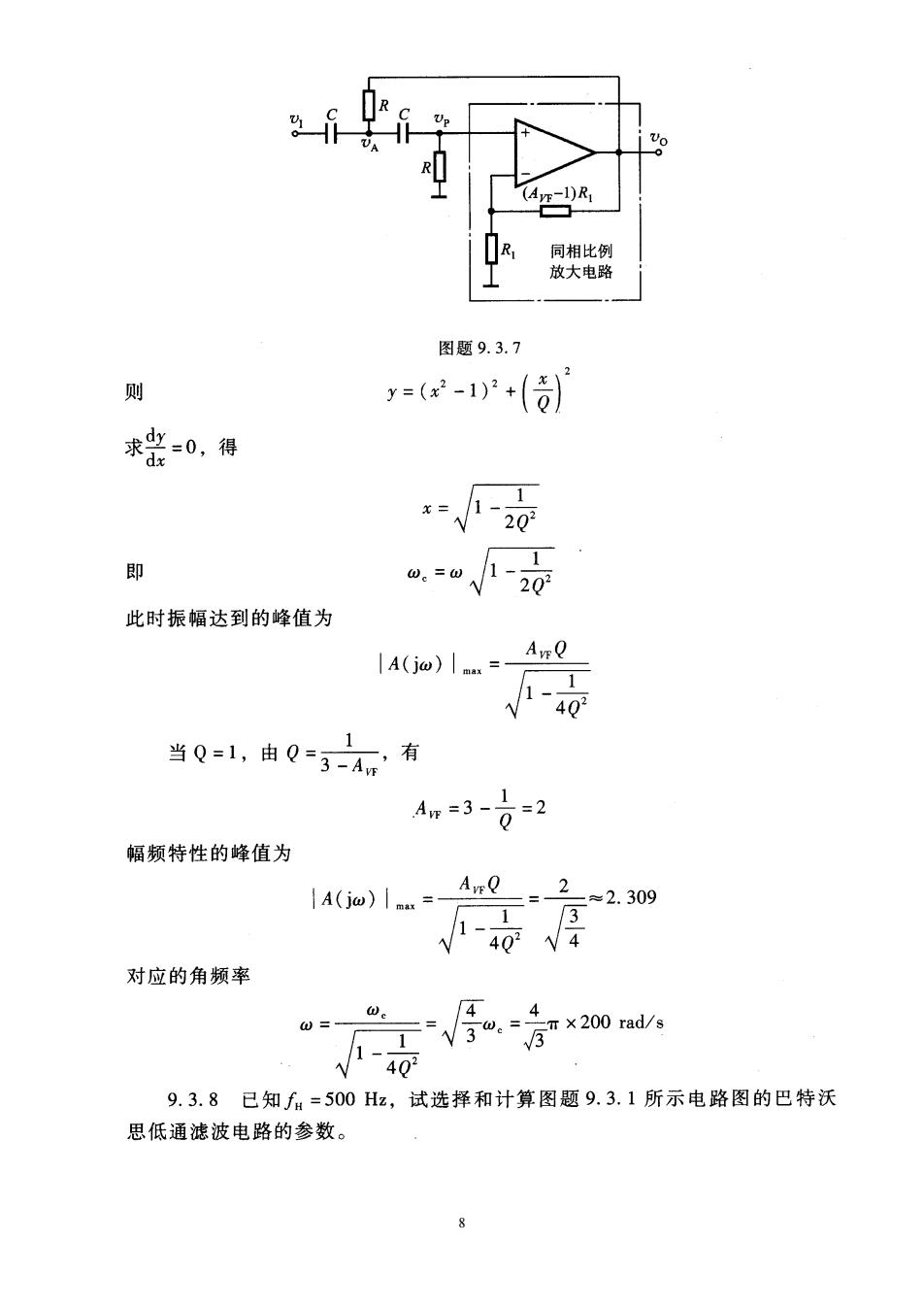
R C 图题9.3.7 则 =12+ 求=0,得 1 即 =u-20 此时振幅达到的峰值为 |A(j@)|a.=- 40 1 当Q=山,由Q=3-A有 Am-3-0=2 幅频特性的峰值为 IA(jo)I=An 2 2.309 0厚 对应的角频率 左√0×2wa 山。 4 0=- - 9.3.8已知f=500Hz,试选择和计算图题9.3.1所示电路图的巴特沃 思低通滤波电路的参数
8

解:(1)根据fa选择和计算C、R值 通常C的容量不应超过1uF,R的阻值应在千欧至兆欧的范围内。 取C=0.1,则由n=2Rc可得 1 R=2mx01×10P×500H3183.1n (2)求R,和R=(Am-1)R, 对于图9.3.1所示电路形式的二阶巴特沃思低通滤波器,对照表9.3.1① 可找出 Ap=1.586 根据Am与R,、R,的关系和集成运放两个输人端外接电阻的对称条件,有 1+是=1.586 RR=R+R 联合求解得R,=172302,R,=10096.8。 由于阻容参数对滤波特性影响较大,R,、R、R和C宜选用精密电阻和电容。 9.3.9试画出下列传递函数的幅频响应曲线,并分别指出各传递函数表 示哪一种(低通、高通)滤波电路(提示:下面各式中的S=s/w。=jω/w.)。 (1)A(S)=g+2S+1 (2)A(S)=St2S+25+1 (3)A(S)=S+29+2S+1 解:(1)A(S)=S+2S+ 1 4) 1-(8)+i5 4) 1-(8T+28 当。=,时,4侣:方得概颜特性如图解93.9所示。这是一个 ①指主教材中的表号,后续章节类似情况均指此意
9
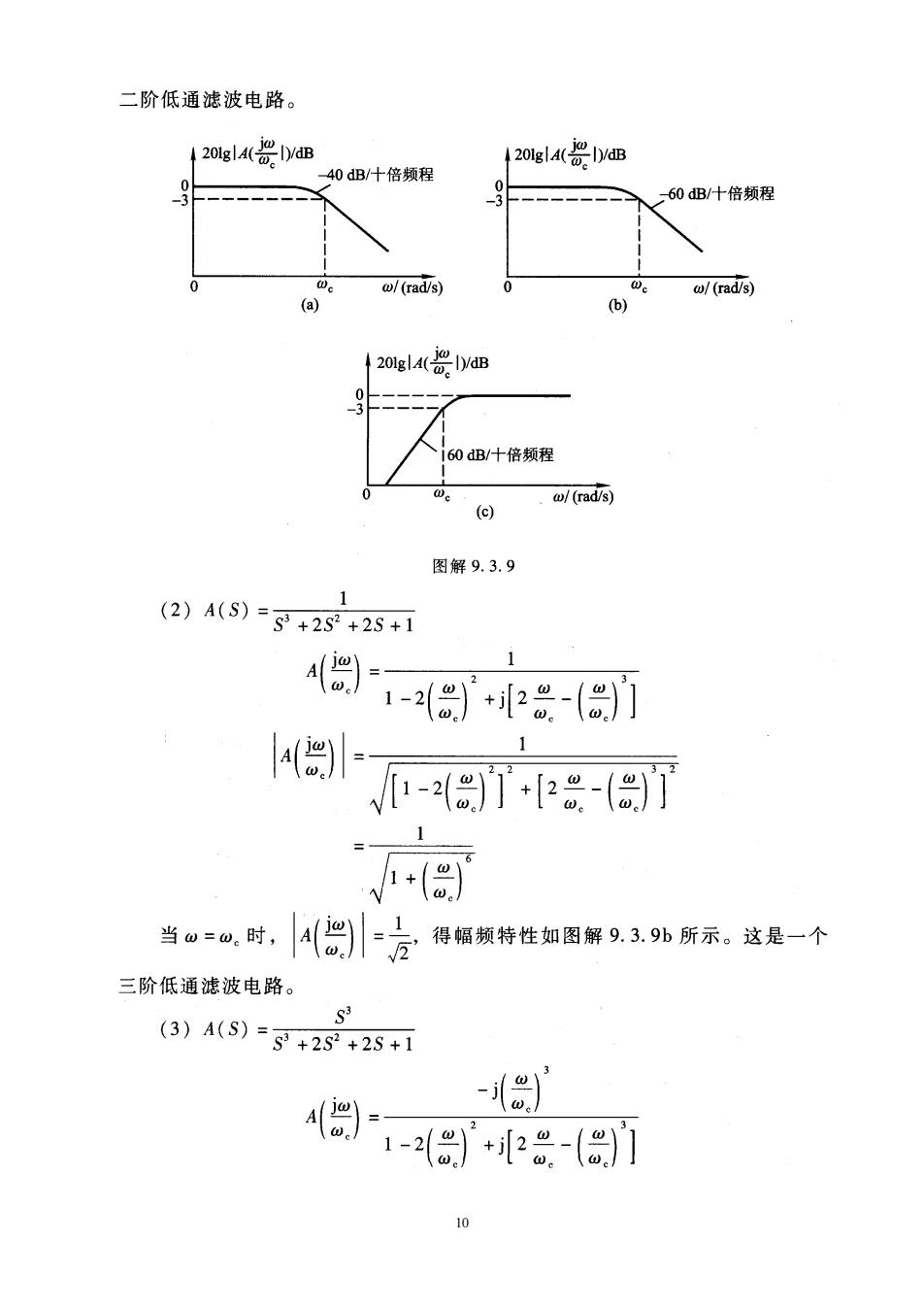
二阶低通滤波电路。 2olgl()/dB 2olgl4x品Iya 40dB/什倍频程 60dB/十倍频程 l(rad/s) (b) /(rad/s) 201gl4(dB 160dB/十倍频程 .l(rad (c) 图解9.39 (2)A(S)=3+29+2S+1 1 9,4受- 1 ae 1-2)T+8-()] +( 当。=“.时,A-方得幅颜特性如图解9.39外所示。这是一个 三阶低通滤波电路。 (3)A(S)=g+29+2S+1 ) 914g
10