
第五章 材料的形变与再结晶 弹性变形 晶体的塑性变形 回复与再结晶 热变形与动态回复、再结晶
第五章 材料的形变与再结晶 弹性变形 晶体的塑性变形 回复与再结晶 热变形与动态回复、再结晶
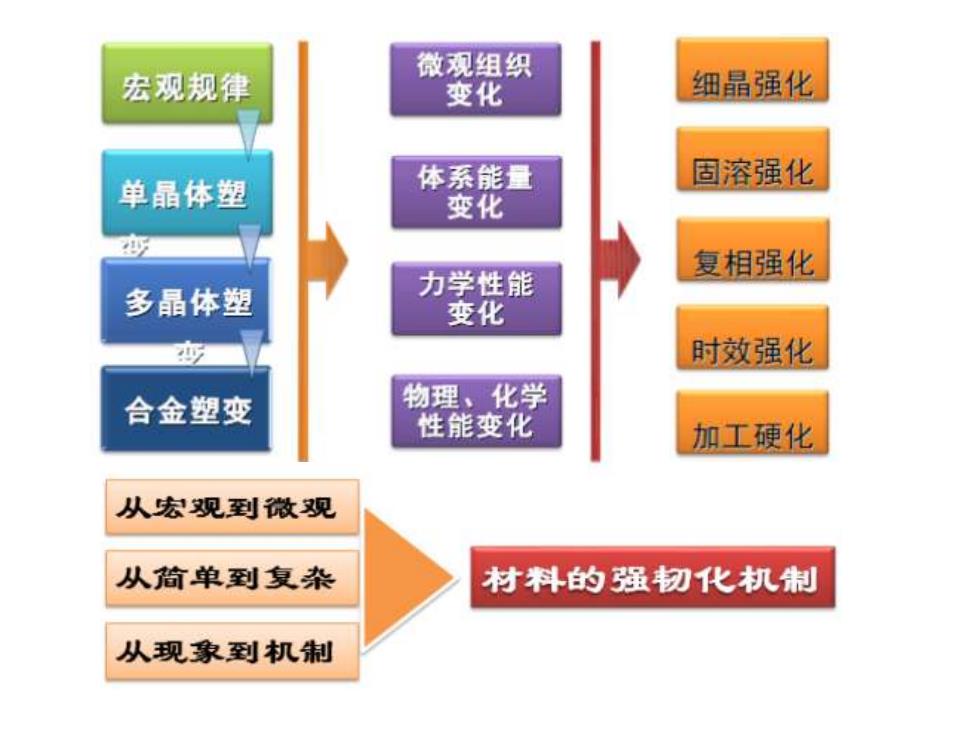
微观组织 宏观规律 变化 细晶强化 体系能量 固溶强化 单晶体塑 变化 变 复相强化 多晶体塑 力学性能 变化 时效强化 合金塑变 物理、化学 性能变化 加工硬化 从宏观到微观 从简单到复杂 材料的强韧化机制 从现象到机制

第一节弹性 金属的应力应变曲线 弹性变形 弹性模量的物理意义 THE END
第一节 弹性 金属的应力-应变曲线 弹性变形 弹性模量的物理意义 THE END SCHOOL OF MATERIALS SCIENCE AND ENGINEERING OF XI`AN JIAOTONG UNIVERSITY
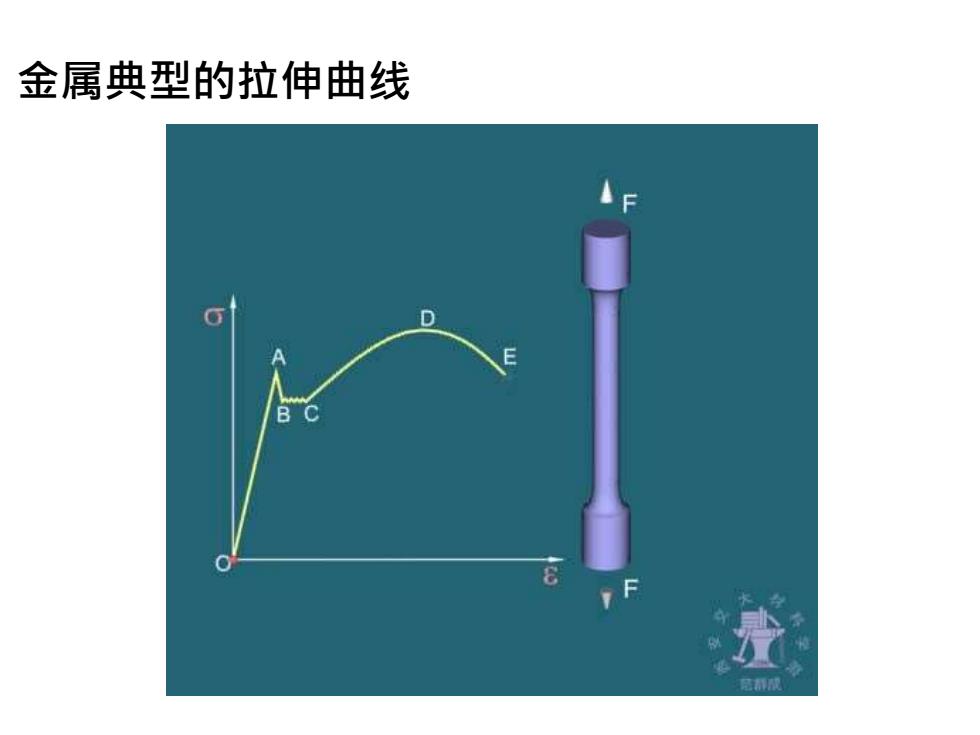
金属典型的拉伸曲线
金属典型的拉伸曲线

、工程应力-应变曲线 1.名阀概念 1)弹性变形: 卸载后可以恢复 塑性变形: 卸载后不可恢复 2) 应力: G= F 应变: = lo
一、工程应力-应变曲线
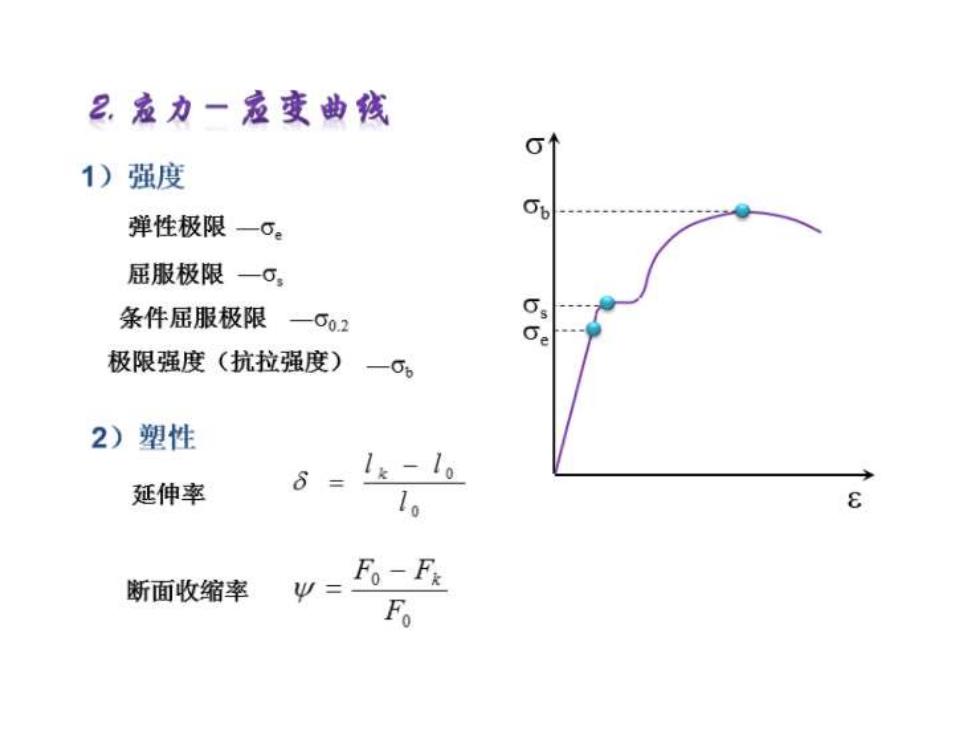
2.寇力一寇变曲线 1)强度 b 弹性极限一σ。 屈服极限一σ, 条件屈服极限一0o,2 6 极限强度(抗拉强度) 一66 2)塑性 延伸率 6= Fo-F 断面收缩率 Fo

3)虎克定律 σ=E·8 E一 杨氏模量 剪切模量 弹性模量 G E、G反映原子间结合力的大小
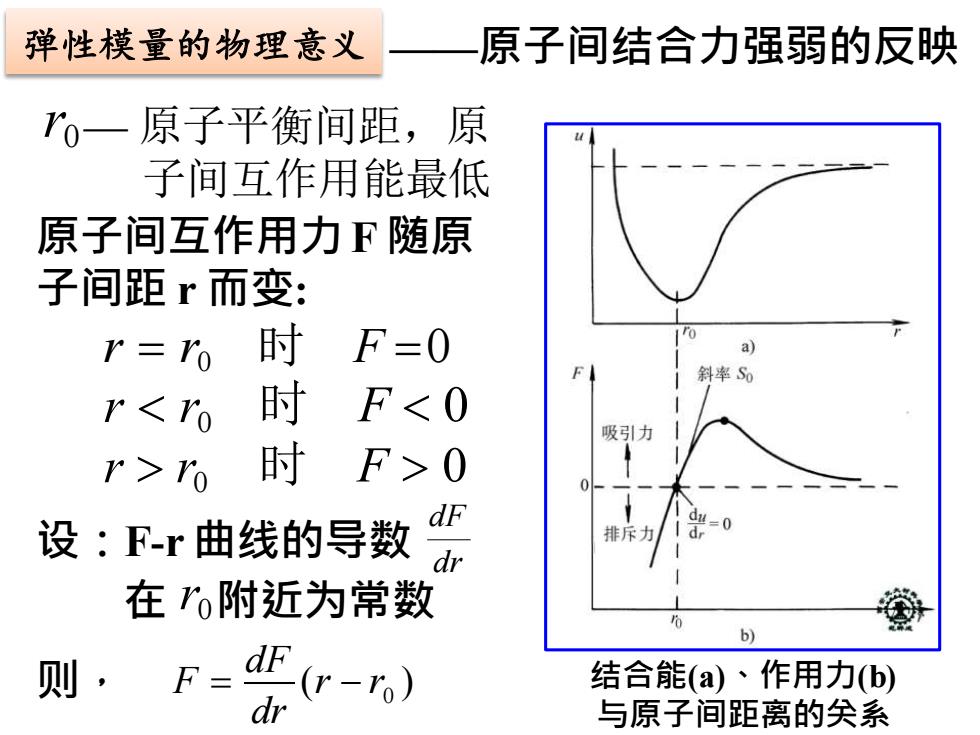
弹性模量的物理意义 原子间结合力强弱的反映 o一原子平衡间距,原 子间互作用能最低 原子间互作用力F随原 子间距r而变: r=ro 时 F=0 a F 斜率S0 rYo 时 F>0 设:F-r曲线的导数 du=0 dr 排斥力1 dr 在ro附近为常数 6 则, F= dF (r-o) 结合能(a)、作用力(b) dr 与原子间距离的矣系
弹性模量的物理意义 ——原子间结合力强弱的反映 结合能(a)、作用力(b) 与原子间距离的关系 r0— 原子平衡间距,原 子间互作用能最低 原子间互作用力F 随原 子间距 r 而变: r = r0 r r0 r r0 时 F =0 时 F 0 时 F 0 设:F-r 曲线的导数 在 r0附近为常数 dr dF 则, 0 dr F = dF (r − r )

F 1 dF r-ro r dr 即 1 dF G .8 ro dr 而虎克定律为 o-E8 故 E=I dF (8-1) rodr 弹性模量是原子间结合力强弱的反映
0 0 0 r r dr r 2 F = 1 dF r −r0 即 r0 dr = 1 dF 而虎克定律为 弹性模量是原子间结合力强弱的反映 . 故 r0 dr = E E = 1 dF (8-1)
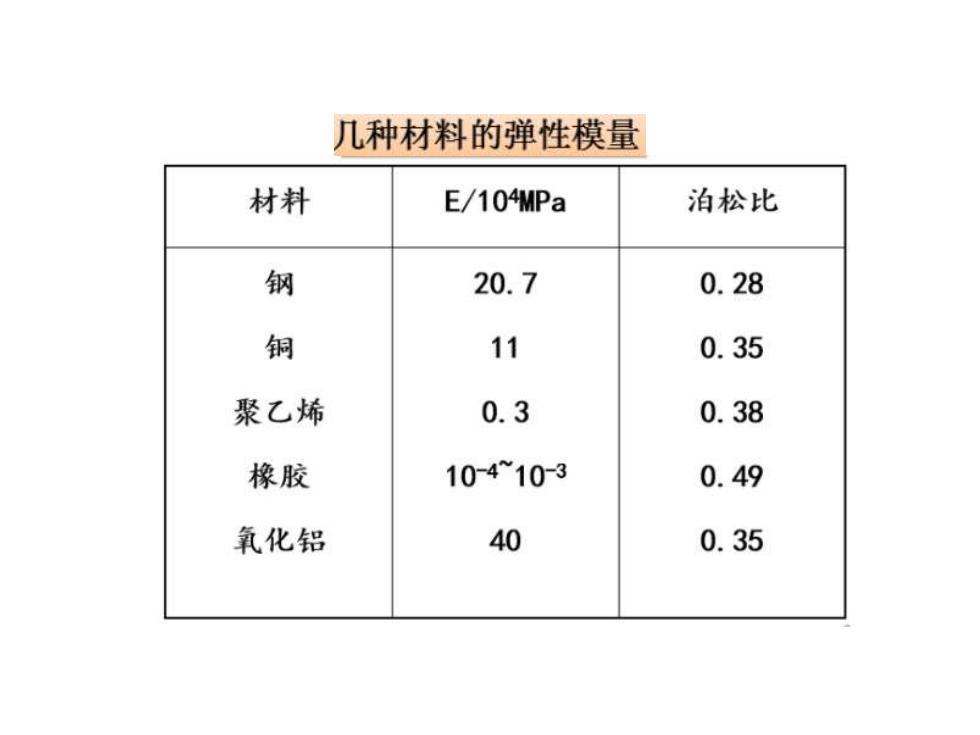
几种材料的弹性模量 材料 E/104MPa 泊松比 钢 20.7 0.28 铜 11 0.35 聚乙烯 0.3 0.38 橡胶 10-410-3 0.49 氧化铝 40 0.35