
第一章绪论 第一章绪论 ·1.1概述 ·1.2数制与代码
第一章 绪 论 第一章 绪 论 • 1.1 概 述 • 1.2 数制与代码
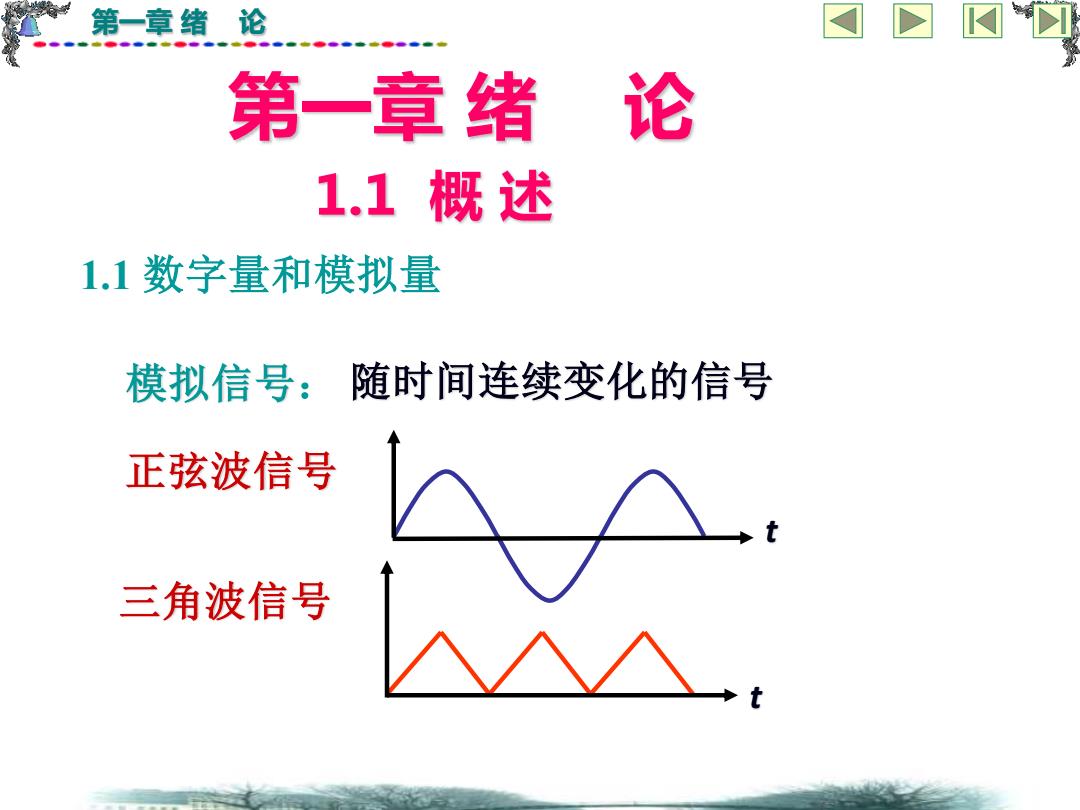
第一章绪论 第一章绪 论 1.1概述 1.1数字量和模拟量 模拟信号:随时间连续变化的信号 正弦波信号 三角波信号
第一章 绪 论 1.1 数字量和模拟量 模拟信号: 随时间连续变化的信号 1.1 概 述 第一章 绪 论 正弦波信号 t 三角波信号 t

第一章绪论 处理模拟信号的电路称为模拟电路。如整流 电路、放大电路等,注重研究的是输入和输出 信号间的大小及相位关系。 在模拟电路中,晶体管三极管通常工作在 放大区
第一章 绪 论 在模拟电路中,晶体管三极管通常工作在 放大区。 处理模拟信号的电路称为模拟电路。如整流 电路、放大电路等,注重研究的是输入和输出 信号间的大小及相位关系

第一章绪论 处理数字信号的电路称为数字电路,它注重研 究的是输入、输出信号之间的逻辑关系。 在数字电路中,晶体管一般工作在截止区和 饱和区,起开关的作用 脉冲信号:是一种跃变信号,并且持续时间 短暂 尖顶波 矩形波
第一章 绪 论 在数字电路中,晶体管一般工作在截止区和 饱和区,起开关的作用 处理数字信号的电路称为数字电路,它注重研 究的是输入、输出信号之间的逻辑关系。 脉冲信号: 是一种跃变信号,并且持续时间 短暂 尖顶波 t 矩形波 t

第一章绪论 1.1.2数字电路特点 1.数字电路易于实现各种控制和决策等应用系统 2.抗干扰能力强,可靠性和准确性高 3.集成度高,通用性强,电路设计维修灵活方便 4.数字信号便于存储,使大量的信息资源可长期 保存数码
第一章 绪 论 1.1.2 数字电路特点 1. 数字电路易于实现各种控制和决策等应用系统 2. 抗干扰能力强,可靠性和准确性高 3. 集成度高,通用性强,电路设计维修灵活方便 4. 数字信号便于存储,使大量的信息资源可长期 保存数码

第一章绪论 1.2数制与代码 1.2.1数制 l.十进制(Decimal)-逢十进一 数码:0~9 位权:10 (12345)10=1×104+2×103+3×102+4×10'+5×10° (143.75)10=1×102+4×101+3×10°+7×10-1+5×10-2 2.二进制(Binary)-逢二进一 数码:0,1 位权:2 (1011)2=1×23+0×22+1×21+1×2° (101.11)2=1×22+0×21+1×2°+1×2-1+1×2-2
第一章 绪 论 1.2.1 数制 1. 十进制(Decimal)-- 逢十进一 数码:0 ~ 9 位权: 4 3 2 1 0 = 110 + 210 + 310 + 4 10 + 5 10 2. 二进制(Binary) -- 逢二进一 数码:0 ,1 位权: 2 ( 1011 ) 3 2 1 0 = 1 2 + 0 2 + 1 2 + 1 2 10 ( 12345 ) i 10i 2 2 1 0 1 2 1 10 4 10 3 10 7 10 5 10 − − ( 143. 75 ) 10 = + + + + 2 ( 101.11 ) 2 1 0 1 2 1 2 0 2 1 2 1 2 1 2 − − = + + + + 1.2 数制与代码

第一章绪论 3.八进制(Octal)-逢八进一 数码:0~7 位权:81 (37.41)8=3×8+7×80+4×8-1+1×8-2 4.十六进制(Hexadecimal)-逢十六进一 数码:0~9,A(10),B(11),C(12),D(13),E(14),F(15) 位权:16 (2A.7F)16=2×16+10×160+7×161+15×16-2 任意W)进制数展开式的普遍形式: D=∑k,N k;一第i位的系数 N一第i位的权
第一章 绪 论 3. 八进制(Octal)-- 逢八进一 数码:0 ~ 7 位权: 8 ( 37. 41 ) 1 0 1 2 3 8 7 8 4 8 1 8 − − = + + + 4. 十六进制 (Hexadecimal) --逢十六进一 数码:0 ~ 9 , A(10) , B(11) , C(12) , D(13) , E(14) , F(15) 位权: i 8 i 16 16 ( 2A. 7F ) 1 0 1 2 2 16 10 16 7 16 15 16 − − = + + + 任意(N)进制数展开式的普遍形式: i D = ki N ki i — 第 i 位的系数 N — 第 i 位的权

第一章绪论 1.2.2数制转换 ()二十转换:将二进制数按位权展开后相加 (101.11)2=1×22+0×2+1×2°+1×2-1+1×2-2 =4+1+0.5+0.25=(5.75)10 (2)十-二转换: 2 26 余数 2 13 除基数 整数的转换--连除法 2 1 得余数 2 3 作系数 (26)10=(11010)2 2 1 1 从低位 1 到高位
第一章 绪 论 1.2.2 数制转换 (1) 二-十转换: 将二进制数按位权展开后相加 2 ( 101.11) 2 1 0 1 2 1 2 0 2 1 2 1 2 1 2 − − = + + + + 10 = 4 +1+ 0. 5 + 0. 25 = (5. 75) (2) 十-二转换: 整数的转换--连除法 10 2 ( 26 ) = ( ) 2 26 13 余数 2 0 2 6 1 2 3 0 2 1 1 0 1 11010 除基数 得余数 作系数 从低位 到高位

第一章绪论 0.8125 取整 小数的转换-一连乘法 X 2 1.6250 (0.8125)10=(0.1101)2 0.6250 X 2 若小数在连乘多次后 1.2500 1 乘基数 不为0,一般按照精确度 0.2500 取整数 要求(如小数点后保留n X 2 作系数 位)得到n个对应位的系 0.5000 0 从高位 数即可。 × 2 到低位 1.0000 快速转换法:拆分法 168421 (26)10=16+8+2=24+23+21=(11010)2
第一章 绪 论 10 2 ( 0. 8125 ) = ( 0. 1101 ) 0. 8125 2 1. 6250 2 1. 2500 2 0. 5000 取整 1 1 0 0. 6250 0. 2500 乘基数 取整数 作系数 从高位 到低位 小数的转换--连乘法 快速转换法:拆分法 ( 26 )10 = 16 + 8 + 2 = 2 4 +23 + 21 = ( 1 1 0 1 0 )2 若小数在连乘多次后 不为 0,一般按照精确度 要求(如小数点后保留 n 位)得到 n 个对应位的系 数即可。 2 1. 0000 1 16 8 4 2 1

第一章绪论 (3)二-八转换:每3位二进制数相当一位8进制数 (010101111)2=(257)8 3388 2 5 (010011100001.000110)2=(2341.06)8 (4)八-二转换:每位8进制数转换为相应3位二进制数 (31.47)g=(011001.100111)2 (375.64)s=(011111101.110100 )2
第一章 绪 论 (3) 二-八转换: 2 8 ( 10 101 111 ) = ( 257 ) 5 7 (4) 八-二转换:每位 8 进制数转换为相应 3 位二进制数 8 2 ( 31. 47 ) = ( 011 001 . 100 111 ) 每 3 位二进制数相当一位 8 进制数 8 2 ( 375. 64 ) = ( 011 111 101 . 110 100 ) 0 2 8 ( 0 10 011 10 0 0 01. 0 0 0 11 0 ) = ( 2 3 4 1 . 0 6 ) 2