
第42卷第6期 北京化工大学学报(自然料学版) Vol.42.No.6 2015年 Beijing University of Chemical Technology (Natural Science 2015 适用生物质及煤热解CD模拟的 DAEM近似计算方法 马趣祁赵系刘辉 (北京化工大学化学工程学院化工资源有效利用国家重点实验室,北京100029) 近似计算方法以使其能够合并在C℉D程序的计算中。简化后的模型能够较精确预测热解产物产率和生成速率:此 外,改进后的模型的计算量大大减少,可适用于较宽泛的加热环境下,且模型预测结果与生物质或煤粒热解实验得 到的结果能够很好的吻合 关键词:生物质;煤粒:热解分布话化能模型 中图分类号:T0530.2:TK6 引言 拟管式沉降炉中小麦秸秆的燃烧,从而得到了小麦 桔轩株烧也可用CFD进行模拟的结论 煤是人类社会重要的能源资源,占世界能源总 分布活化能模型(DAEM)也称为多重反应模 量的22%,但同时煤也是不可再生资源。因此在倡 (MRM),已成为热解过程研究中应用最泛的模 导低碳环保的背景下,生物质无疑是一种较好的替 型。在分布活化能模型提出后,Donskoi等对求解 代能源。因热解过程是生物质转化的第一步,之后 分布活化能模型进行了进一步的探索,并基于高斯: 还要经历如气化、液化、干馏及燃烧等过程,故研究 埃尔米特求积公式(Gaus-Hermite Quadrature)提 生物质热解对生物质能源的发展有很大的帮助。 出了改进的积分公式(MGHQ):通过将此方法与其 如今,模拟计算已成为研究煤和生物质热解及 他近似方法进行对比,验证了此方法具有更高的精 燃烧的必不可少的方法之一。例如计算流体力学 度。但是通过此方法近似后,仍存在复杂的温度积 (CD)商业软件已经句含了大量的用于计算化石燃 分,偶合在CFD中时计算量仍然很大 料的燃烧模型。通过程序模拟复杂的热解过程可以 本文在文献[4]求解DAEM的基础上引人了 更好地分析设计及优化生物质及煤粒的燃烧和封 度积分和广义温度积分形式的近似们,在保证精度 化过程。Eaon等)运用CFD软件模拟了煤燃烧过 的前提下简化了复杂的二重积分。此方法适用于模 程,并与实验数据对比,有很好的一致性:此外,作者 拟计算线性和简单非线性升温条件下煤或生物质的 也强调了要简化计算模型来节省计算时间。 热解过程。通过与已有文献结果和实验数据对比, liams等2]通过类比煤燃烧过程,论证了煤燃烧的研 进一步验证了本文方法的可靠性。 究方法也适用于生物质的燃烧,其中,脱挥发分也即 热解过程,是燃烧过程中最重要的过程。Jones等3) DAEM的建立及近似优化 对小麦秸秆的燃烧特性进行了模拟,将模拟得到的 L.1DAEM的建立 产物产率作为模型参数输人至C℉D模型中,用以模 分布活化能模型假设热解过程包含了无限多个 独立的一级不可可逆化学反应。这些化学反应的热解 收稿日期.2015-04-1 基金项目 速率可以用以下方程表示 国家“973"计划(2011CB201306 第一作者:女,1989年生,硕士生 立=(-y) d (1 ◆通讯联系人 式中表示某个独立的化学反应或某个反应物,V E-mail.hliu@mail.buct.edu.en 表示对于第i个化学反应或某个反应物,从零时刻 http://www.journal.buct.edu.cn
第 42 卷 第 6 期 2015 年 北京化工大学学报(自然科学版) Journal of Beijing University of Chemical Technology (Natural Science) Vol. 42, No. 6 2015 适用生物质及煤热解 CFD 模拟的 DAEM 近似计算方法 马艺桠 祁 娟 赵欣磊 刘 辉* (北京化工大学 化学工程学院 化工资源有效利用国家重点实验室, 北京 100029) 摘 要: 生物质以及煤粒的复杂热解反应可用分布活化能模型(DAEM)模拟,但将此模型直接应用于计算流体力 学(CFD)模拟计算量极大,因为在每个时间步中对每个计算网格都要计算多重积分。 因此,本文提出了 DAEM 的 近似计算方法以使其能够合并在 CFD 程序的计算中。 简化后的模型能够较精确预测热解产物产率和生成速率;此 外,改进后的模型的计算量大大减少,可适用于较宽泛的加热环境下,且模型预测结果与生物质或煤粒热解实验得 到的结果能够很好的吻合。 关键词: 生物质; 煤粒; 热解; 分布活化能模型 中图分类号: TQ530郾 2;TK6 收稿日期: 2015-04-13 基金项目: 国家“973冶计划(2011CB201306) 第一作者: 女,1989 年生,硕士生 *通讯联系人 E鄄mail: hliu@ mail. buct. edu. cn 引 言 煤是人类社会重要的能源资源,占世界能源总 量的 22% ,但同时煤也是不可再生资源。 因此在倡 导低碳环保的背景下,生物质无疑是一种较好的替 代能源。 因热解过程是生物质转化的第一步,之后 还要经历如气化、液化、干馏及燃烧等过程,故研究 生物质热解对生物质能源的发展有很大的帮助。 如今,模拟计算已成为研究煤和生物质热解及 燃烧的必不可少的方法之一。 例如计算流体力学 (CFD)商业软件已经包含了大量的用于计算化石燃 料的燃烧模型。 通过程序模拟复杂的热解过程可以 更好地分析、设计及优化生物质及煤粒的燃烧和转 化过程。 Eaton 等[1]运用 CFD 软件模拟了煤燃烧过 程,并与实验数据对比,有很好的一致性;此外,作者 也强调了要简化计算模型来节省计算时间。 Wil鄄 liams 等[2]通过类比煤燃烧过程,论证了煤燃烧的研 究方法也适用于生物质的燃烧,其中,脱挥发分也即 热解过程,是燃烧过程中最重要的过程。 Jones 等[3] 对小麦秸秆的燃烧特性进行了模拟,将模拟得到的 产物产率作为模型参数输入至 CFD 模型中,用以模 拟管式沉降炉中小麦秸秆的燃烧,从而得到了小麦 秸秆燃烧也可用 CFD 进行模拟的结论。 分布活化能模型(DAEM)也称为多重反应模型 (MRM),已成为热解过程研究中应用最广泛的模 型。 在分布活化能模型提出后,Donskoi 等[4]对求解 分布活化能模型进行了进一步的探索,并基于高斯- 埃尔米特求积公式(Gauss - Hermite Quadrature) 提 出了改进的积分公式(MGHQ);通过将此方法与其 他近似方法进行对比,验证了此方法具有更高的精 度。 但是通过此方法近似后,仍存在复杂的温度积 分,耦合在 CFD 中时计算量仍然很大。 本文在文献[4]求解 DAEM 的基础上引入了温 度积分和广义温度积分形式的近似[5] ,在保证精度 的前提下简化了复杂的二重积分。 此方法适用于模 拟计算线性和简单非线性升温条件下煤或生物质的 热解过程。 通过与已有文献结果和实验数据对比, 进一步验证了本文方法的可靠性。 1 DAEM 的建立及近似优化 1郾 1 DAEM 的建立 分布活化能模型假设热解过程包含了无限多个 独立的一级不可逆化学反应。 这些化学反应的热解 速率可以用以下方程表示 dVi dt = ki(V * i - Vi) (1) 式中 i 表示某个独立的化学反应或某个反应物,Vi 表示对于第 i 个化学反应或某个反应物,从零时刻 http://www.journal.buct.edu.cn

第6期 马艺桠等:适用生物质及煤热解CFD模拟的DAEM近似计算方法 .27. 开始至某时刻热解析出的挥发分(质量分数), 为对应第:个多项式零点的活化能。利用式 是当:一x时V的值,速率常数k,由阿伦尼乌斯方程 (9),则式(8)可化为下列形式 给出 v=v_V k=kep(-7o】 E. (2) 式中为指前因子,E为第:个化学反应的表观活 d (11) 化能,R为理想气体常数,T为绝对温度。对式(1) Donskoi等指出相比其他求积方法,直接用高 积分得 斯-埃尔米特求积公式并没有提高精度,因为离分 =g-vep-「k.d】 布中心远的节点并没有对积分做出贡献,故引人重 (3) 调节因子m问 假设反应数目足够大,则活化能的分布可以用 E=E。+Y,√2m (12 分布函数(E)表示。令Vf(E)dE表示活化能介 且类比于式(9),得到了改进后的积分公式 于E和E+E之间的潜在挥发分部分,有 (MGHO dv,=Vf(E)dE (4) 根据活化能分布的定义有 g)dy=Ae()g) (13 厂fE)d证=l (5) 利用式(13),则式(8)可化为下列形式 通常E)可用高斯分布来表示6,若平均活化 =p-m Aep()ep() 2 能为E。,标准方差为σ,可得 f(E)=- (6) em【-4.即(-0出】 (14) 2r2 虽然方程形式看起来复杂化了,但是将外层积 从零时刻开始至某时刻:的挥发量为 v=r-rem(-a(E)KE)E 分化为相对简单的ep[仁(二)']以及m/√后 2o 的计算,减少了计算量 (7) 1.2.2线性升温条件下的近似 将式(2)和(6)代入式(7)中,可得 式(14)仍存在复杂的积分,为进一步简化计 算,对该式中的温度积分做了近似处理。 对于单一分解反应,速率方程通常由阿伦尼乌 (8) 斯方程(式(2))表示 式(8)即为分布活化能模型的积分表达式。由 柴-ep(7) (15】 该式可见,当将其直接应用于CD程序中计算热解 其中,x为转化率,八x)代表反应机理函数。 挥发量时,由于每一时间步中对每个计算网格都要 当反应在线性升温环境下进行,即T()=T。 计 二重积分,计算代价很高昂。故本文对 b,其中T,是初始温度,b是加热速率,则式(15)为 DAEM进行了近似计算。 L.2DAEM的近似求解 步-w(-后) (16) 1.21高斯-埃尔米特求积公式 分离变量后得 用高斯-埃尔米特求积公式近似求解 eg(y)dy=∑A,g() (9) 即(后)r (17 其中g(y)为被积函数,,是埃尔米特多项式的零 0到T间四(-后)积分相比于0到T间积 点,A为求积系数[),本文取n=6。令 分通常可以忽略,故可得 方~ (10) 告-会em(-后)ar (18】 http://www.journal.buct.edu.cn
开始至某时刻 t 热解析出的挥发分(质量分数),V * i 是当 t寅肄 时 Vi的值,速率常数 ki由阿伦尼乌斯方程 给出 ki = k0 exp ( - Ei RT(t ) ) (2) 式中 k0为指前因子,Ei为第 i 个化学反应的表观活 化能,R 为理想气体常数,T 为绝对温度。 对式(1) 积分得 Vi = V * i - V * i exp ( - 乙 t 0 kidt ) (3) 假设反应数目足够大,则活化能的分布可以用 分布函数 f(E)表示。 令 V * i f(E) dE 表示活化能介 于 E 和 E + dE 之间的潜在挥发分部分,有 dVi = V * i f(E)dE (4) 根据活化能分布的定义有 乙 肄 0 f(E)dE = 1 (5) 通常 f(E)可用高斯分布来表示[6] ,若平均活化 能为 E0 ,标准方差为 滓,可得 f(E) = 1 滓 2仔 exp ( - (E - E0 ) 2 2滓 2 ) (6) 从零时刻开始至某时刻 t 的挥发量为 V = V * - V * 乙 肄 0 exp ( - 乙 t 0 k(E)dt )f(E)dE (7) 将式(2)和(6)代入式(7)中,可得 V = V * - V * 滓 2仔 乙 肄 0 exp [ - k0 乙 t 0 exp ( - E RT(t ) ) dt - ( (E - E0 ) 2 2滓 2 ) ] dE (8) 式(8)即为分布活化能模型的积分表达式。 由 该式可见,当将其直接应用于 CFD 程序中计算热解 挥发量时,由于每一时间步中对每个计算网格都要 计算 二 重 积 分[4] , 计 算 代 价 很 高 昂。 故 本 文 对 DAEM 进行了近似计算。 1郾 2 DAEM 的近似求解 1郾 2郾 1 高斯-埃尔米特求积公式 用高斯-埃尔米特求积公式近似求解[4] 乙 +肄 -肄 e - y 2 g(y)dy抑 移 n i = 1 Aig(yi) (9) 其中 g( y) 为被积函数,yi 是埃尔米特多项式的零 点,Ai为求积系数[7] ,本文取 n = 6。 令 yi = E忆i - E0 2滓 (10) E忆i 为对应第 i 个多项式零点的活化能。 利用式 (9),则式(8)可化为下列形式 V = V * - V * 仔 移 n i =1 Ai exp [ - k0 乙 t 0 exp ( - E忆i RT(t ) ) dt ] (11) Donskoi 等[4]指出相比其他求积方法,直接用高 斯-埃尔米特求积公式并没有提高精度,因为离分 布中心远的节点并没有对积分做出贡献,故引入重 调节因子 m [4] E忆i = E0 + yi 2滓m (12) 且类比于式 (9 ),得到了改进后的积分公式 (MGHQ) 乙 +肄 -肄 g(y)dy抑 移 n i = 1 Ai exp (y 2 i )g(yi) (13) 利用式(13),则式(8)可化为下列形式 V = V * - V *m 仔 移 n i =1 Ai exp(y 2 i )exp ( - (E忆i - E0 ) 2 2滓 2 ) exp [ - k0 乙 t 0 exp ( - E忆i RT(t ) ) dt ] (14) 虽然方程形式看起来复杂化了,但是将外层积 分化为相对简单的 exp [ - (E忆i - E0 ) 2 2滓 2 ] 以及 m / 仔 的计算,减少了计算量。 1郾 2郾 2 线性升温条件下的近似 式(14) 仍存在复杂的积分,为进一步简化计 算,对该式中的温度积分做了近似处理。 对于单一分解反应,速率方程通常由阿伦尼乌 斯方程(式(2))表示 dx dt = k0 exp ( - E RT(t ) ) f(x) (15) 其中,x 为转化率, f(x)代表反应机理函数。 当反应在线性升温环境下进行,即 T(t) = T0 + bt,其中 T0是初始温度,b 是加热速率,则式(15)为 dx dT = k0 b exp ( - E ) RT f(x) (16) 分离变量后得 乙 x 0 dx f(x) = k0 b 乙 T T0 exp ( - E ) RT dT (17) 0 到 T0间 exp ( - E ) RT 积分相比于 0 到 T 间积 分通常可以忽略,故可得 乙 x 0 dx f(x) = k0 b 乙 T 0 exp ( - E ) RT dT (18) 第 6 期 马艺桠等: 适用生物质及煤热解 CFD 模拟的 DAEM 近似计算方法 ·27· http://www.journal.buct.edu.cn

·28 北京化工大学学报(自然科学版) 2015年 式(18)等号右边的积分为温度积分,没有解析 解,需要近似计算,令=E/RT rm(-)r=(层)- (层)pu) (26) 2 P(u) (19) p(u)=∫广e(-h 3 (27) Oao)总结了p(u)的近似式 广义温度积分的形式为 p(u)'=p-"2Q(u》 (20 本文在保证高精度的前提下选择了式(21)句 (u.) (28) +18w3+86u2+96u 可近似为 Q(u)=+20+120+240a+120 (21 pu,p)=p(Q(u) (29) 式(21)近似相对误差为 故式(27)中p(u)与广义温度积分中=1时的 81='-1 (22) p(u) 形式是一样的,可选择近似式 其中p(u)'为近似值,p(u)为原积分值。误差结果 u+13u3+36u2+12u (30) 见表1。 Q(w)=c+16m+722+96u+24 表1p(“)的相对误差低于指定值时“的取值范围 验证误差8,1如图1所示。由图1可知在u [1,5]时,误差较大。但结合煤或生物质热解温度 Table 1 Intervals of u that guarantee relative deviation T和E的值,不会在此区间内取值,所以该近似式 of p(u)lower than the indicated values 是较精确的。 18.1<1毫18.1<0.5%18.1<0.1毫18,1<0.05%181<0.02% 16 1 u≥1.5 ≥2 w≥2.5 u≥3.5 对于煤热解,∈[1,250],可以保证精度。即 当T(t)=T。+bL时,DAEM化为 v=r-立Aep()ep(-m)e [-R 2+18m23+862+96u Γn+20m+120m2+240u+120 50100150200 (23】 图1u∈[1,250]时16,1的值 1.2.3非线性升温条件下的近似 Fig.The absolute value of the relative deviation 由于实际应用于CD时,通常输人的温度环境 when [1.250] 不能满足线性升温,一般为非线性升温,所以提出了 即当aT(t)=T。+bt时,DAEM化为 此种情形下的近似 通常非线性升温下温时关系满足a严(t)=T。+ em【-2()即- em(后ar-2m(-是)n 4+13u3+36m2+12u (24) +16m+722+96u+24 (31) 同理,忽略0到T,间exp(-E/T)积分得 2结果与讨论 kem(-后)r=2学a(-后)r 为了验证上述模型的可靠性,本文用Matlab程序 (25) 模拟生物质及煤热解过程,并分别选择了已有文献中 令u=E/RT 的实验数据和其模拟数据进行对比,计算结果如下。 http://www.journal.buct.edu.cn
式(18)等号右边的积分为温度积分,没有解析 解,需要近似计算,令 u = E / RT 乙 T 0 exp ( - E ) RT dT = E R 乙 肄 u exp ( - u) u 2 du = E R p(u) (19) 譫rf觔o [5]总结了 p(u)的近似式 p(u)忆 = exp ( - u) u 2 Q(u) (20) 本文在保证高精度的前提下选择了式(21) [5] Q(u) = u 4 + 18u 3 + 86u 2 + 96u u 4 + 20u 3 + 120u 2 + 240u + 120 (21) 式(21)近似相对误差为 | 啄r | = p(u)忆 p(u) - 1 (22) 其中 p(u)忆为近似值,p( u)为原积分值。 误差结果 见表 1。 表 1 p(u)的相对误差低于指定值时 u 的取值范围 Table 1 Intervals of u that guarantee relative deviations of p(u) lower than the indicated values | 啄r | < 1% | 啄r | < 0郾 5% | 啄r | < 0郾 1% | 啄r | < 0郾 05% | 啄r | < 0郾 02% u逸1 u逸1郾 5 u逸2 u逸2郾 5 u逸3郾 5 对于煤热解,u沂[1,250],可以保证精度。 即 当 T(t) = T0 + bt 时,DAEM 化为 V = V * - V *m 仔 移 n i = 1 Ai exp ( y 2 i ) exp ( - y 2 i m 2 ) [ exp - E忆i k0 bR exp ( - u) u 2 u 4 + 18u 3 + 86u 2 + 96u u 4 + 20u 3 + 120u 2 + 240u ] + 120 (23) 1郾 2郾 3 非线性升温条件下的近似 由于实际应用于 CFD 时,通常输入的温度环境 不能满足线性升温,一般为非线性升温,所以提出了 此种情形下的近似。 通常非线性升温下温时关系满足 aT 2 (t) = T0 + bt。 乙 t 0 k0 exp ( - E ) RT dT = 乙 T T0 2k0 aT b exp ( - E ) RT dT (24) 同理,忽略 0 到 T0间 exp( - E / RT)积分得 乙 t 0 k0 exp ( - E ) RT dT = 2k0 a b 乙 T 0 Texp ( - E ) RT dT (25) 令 u = E / RT 乙 T 0 Texp ( - E ) RT dT = ( ) E R 2 乙 肄 u exp ( - u) u 3 du ( = ) E R 2 p(u) (26) p(u) = 乙 肄 u exp ( - u) u 3 du (27) 广义温度积分的形式为 p(u,v) = 乙 肄 u exp ( - u) u v + 2 du (28) 可近似为 p(u,v) = exp ( - u) u v + 2 Q(u) (29) 故式(27)中 p(u)与广义温度积分中 v = 1 时的 形式是一样的,可选择近似式 Q(u) = u 4 + 13u 3 + 36u 2 + 12u u 4 + 16u 3 + 72u 2 + 96u + 24 (30) 验证误差| 啄r | 如图 1 所示。 由图 1 可知在 u沂 [1, 5]时,误差较大。 但结合煤或生物质热解温度 T 和 E 的值,u 不会在此区间内取值,所以该近似式 是较精确的。 图 1 u沂[1,250]时| 啄r |的值 Fig. 1 The absolute value of the relative deviations when u沂[1,250] 即当 aT 2 (t) = T0 + bt 时,DAEM 化为 V = V * - V *m 仔 移 n i = 1 Ai exp(y 2 i )exp( - y 2 i m 2 ) exp [ - 2k0 a ( b E忆i ) R 2 exp ( - u) u 3 u 4 + 13u 3 + 36u 2 + 12u u 4 + 16u 3 + 72u 2 + 96u ] + 24 (31) 2 结果与讨论 为了验证上述模型的可靠性,本文用 Matlab 程序 模拟生物质及煤热解过程,并分别选择了已有文献中 的实验数据和其模拟数据进行对比,计算结果如下。 ·28· 北京化工大学学报(自然科学版) 2015 年 http://www.journal.buct.edu.cn
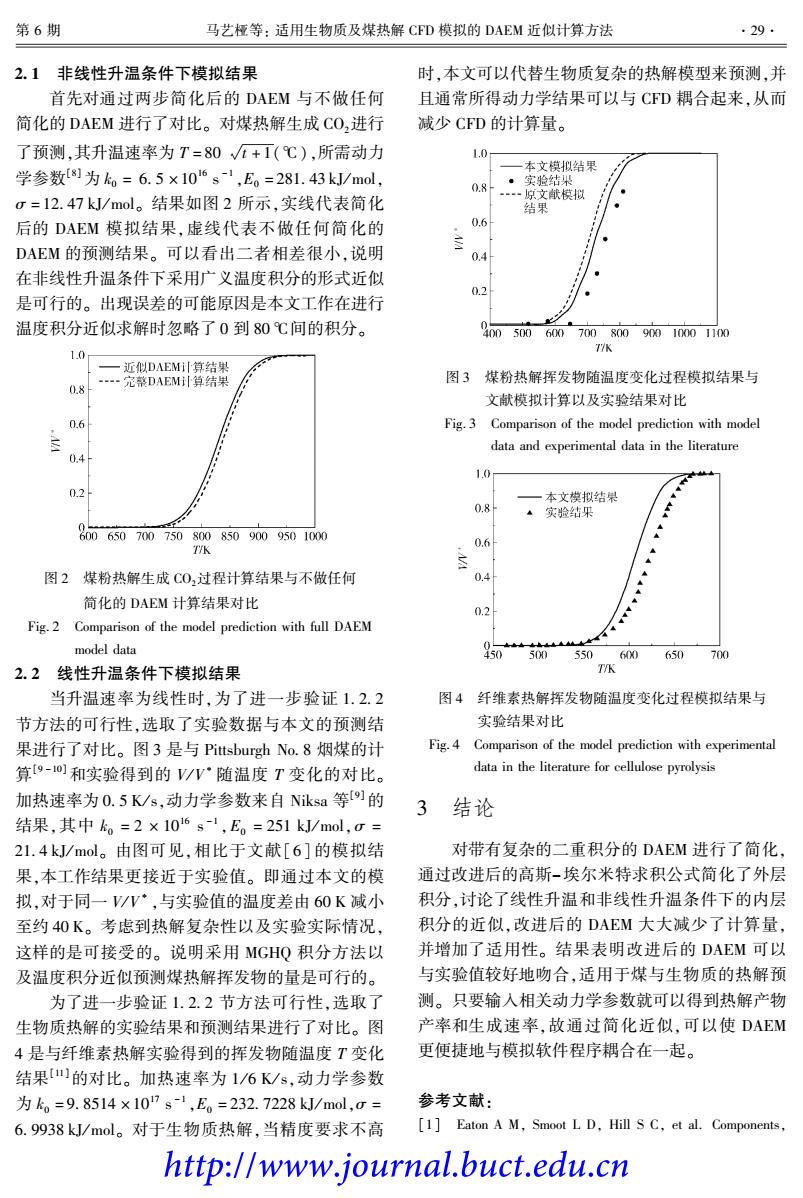
第6期 马艺桠等:适用生物质及煤热解CFD模拟的DAEM近似计算方法 .29 2.1非线性升温条件下模拟结果 时,本文可以代替生物质复杂的热解模型来预测,并 首先对通过两步简化后的DAEI与不做任何 且通常所得动力学结果可以与CFD越合起来,从而 简化的DAEM进行了对比。对煤热解生成CO,进行 减少CFD的计算量。 了预测其升温速率为T=80+1(℃),所需动力 学参数8为k=6.5×10“-,E。=281.43kJ/m0l r=12.47kJ/mol。结果如图2所示,实线代表简化 后的DAEM模拟结果,虚线代表不做任何简化的 DAEM的预侧结果。可以看出二者相差很小,说明 在非线性升温条件下采用广义温度积分的形式近位 是可行的。出现误差的可能原因是本文工作在进行 温度积分近似求解时忽略了0到80℃间的积分 0n50060070901010 10 图3煤粉热解挥发物随温度变化过程模拟结果与 文献模拟计算以及实验结果对比 Fig.3 Comparison of the model prediction with model data and experimental data in the literature 1.0 02 08! 颂商7m7000001 图2煤粉热解生成C0过程计算结果与不做任何 简化的DAEM计算结果对比 02 Fig.2 Comparison of the model prediction with full DAEM model data 650 2.2线性升温条件下模拟结果 当升温速率为线性时,为了进一步验证1.2.2 图4纤维素热解挥发物随温度变化过程模拟结果与 节方法的可行性,选取了实验数据与本文的预测结 实验结果对比 果进行了对比。图3是与ittsburgh No.8烟煤的计 算-o和实验得到的V/N~随温度T变化的对比, data in the lite 加热速率为0.5K/s,动力学参数来自Nksa等)的 3 结论 结果,其中k。=2×106s-1,E。=251kJ/ml, 21.4kJ/mol。由图可见,相比于文献[6]的模拟结 对带有复杂的二重积分的DAEM进行了简化 果,本工作结果更接近于实验值。即通过本文的模 通过改进后的高斯-埃尔米特求积公式简化了外层 拟,对于同一/p,与实验值的温度差由60K减小 积分,讨论了线性升温和非线性升温条件下的内层 至约40K。考虑到热解复杂性以及实验实际情况」 积分的近似,改进后的DAEM大大减少了计算量 这样的是可接受的。说明采用MGHQ积分方法以 并增加了适用性。结果表明改进后的DAEM可以 及温度积分沂似预测煤热解挥发物的量是可行的 与实验值较好地吻合,适用于煤与生物质的热解而 为了进一步验证1.2.2节方法可行性,选取了 测。只要输入相关动力学参数就可以得到热解产物 生物质热解的实验结果和预测结果进行了对比。图 产率和生成速率,故通过简化近似,可以使DAEM 4是与纤维素热解实验得到的挥发物随温度T变化 更便捷地与模拟软件程序耦合在一起。 结果)的对比。加热速率为1/6K/5,动力学参数 为k。=9.8514×10”-,E。=232.7228J/m0l,= 参考文献 6.9938k/mol。对于生物质热解,当精度要求不高 [1]Eaton A M,Smoot L D.Hill S C,et al.Components http://www.journal.buct.edu.cn
2郾 1 非线性升温条件下模拟结果 首先对通过两步简化后的 DAEM 与不做任何 简化的 DAEM 进行了对比。 对煤热解生成 CO2进行 了预测,其升温速率为 T = 80 t + 1(益 ),所需动力 学参数[8]为 k0 = 6郾 5 伊 10 16 s - 1 ,E0 = 281郾 43 kJ/ mol, 滓 = 12郾 47 kJ/ mol。 结果如图 2 所示,实线代表简化 后的 DAEM 模拟结果,虚线代表不做任何简化的 DAEM 的预测结果。 可以看出二者相差很小,说明 在非线性升温条件下采用广义温度积分的形式近似 是可行的。 出现误差的可能原因是本文工作在进行 温度积分近似求解时忽略了 0 到 80 益间的积分。 图 2 煤粉热解生成 CO2过程计算结果与不做任何 简化的 DAEM 计算结果对比 Fig. 2 Comparison of the model prediction with full DAEM model data 2郾 2 线性升温条件下模拟结果 当升温速率为线性时,为了进一步验证 1郾 2郾 2 节方法的可行性,选取了实验数据与本文的预测结 果进行了对比。 图 3 是与 Pittsburgh No郾 8 烟煤的计 算[9 - 10]和实验得到的 V / V * 随温度 T 变化的对比。 加热速率为 0郾 5 K/ s,动力学参数来自 Niksa 等[9] 的 结果,其中 k0 = 2 伊 10 16 s - 1 ,E0 = 251 kJ/ mol,滓 = 21郾 4 kJ/ mol。 由图可见,相比于文献[6] 的模拟结 果,本工作结果更接近于实验值。 即通过本文的模 拟,对于同一 V / V * ,与实验值的温度差由 60 K 减小 至约 40 K。 考虑到热解复杂性以及实验实际情况, 这样的是可接受的。 说明采用 MGHQ 积分方法以 及温度积分近似预测煤热解挥发物的量是可行的。 为了进一步验证 1郾 2郾 2 节方法可行性,选取了 生物质热解的实验结果和预测结果进行了对比。 图 4 是与纤维素热解实验得到的挥发物随温度 T 变化 结果[11]的对比。 加热速率为 1 / 6 K/ s,动力学参数 为 k0 = 9郾 8514 伊 10 17 s - 1 ,E0 = 232郾 7228 kJ/ mol,滓 = 6郾 9938 kJ/ mol。 对于生物质热解,当精度要求不高 时,本文可以代替生物质复杂的热解模型来预测,并 且通常所得动力学结果可以与 CFD 耦合起来,从而 减少 CFD 的计算量。 图 3 煤粉热解挥发物随温度变化过程模拟结果与 文献模拟计算以及实验结果对比 Fig. 3 Comparison of the model prediction with model data and experimental data in the literature 图 4 纤维素热解挥发物随温度变化过程模拟结果与 实验结果对比 Fig. 4 Comparison of the model prediction with experimental data in the literature for cellulose pyrolysis 3 结论 对带有复杂的二重积分的 DAEM 进行了简化, 通过改进后的高斯-埃尔米特求积公式简化了外层 积分,讨论了线性升温和非线性升温条件下的内层 积分的近似,改进后的 DAEM 大大减少了计算量, 并增加了适用性。 结果表明改进后的 DAEM 可以 与实验值较好地吻合,适用于煤与生物质的热解预 测。 只要输入相关动力学参数就可以得到热解产物 产率和生成速率,故通过简化近似,可以使 DAEM 更便捷地与模拟软件程序耦合在一起。 参考文献: [1] Eaton A M, Smoot L D, Hill S C, et al. Components, 第 6 期 马艺桠等: 适用生物质及煤热解 CFD 模拟的 DAEM 近似计算方法 ·29· http://www.journal.buct.edu.cn

·30· 北京化工大学学报(自然科学版) 2015年 formulations,solutions,evaluation,and application of (in Chinese) comprehensive combustion models[J].Progress in Ener- [7]邓建中,刘之行.计算方法[M.2版.西安:西安交 gy and Combustion Science,1999,25(4):387-436. 通大学出版社,2001. [2] Williams A,Pourkashanian M,Jones J M.Combustion of Deng JZ,Liu Z X.Computational method[M].2nd ed. pulverised coal and biomass[J].Progress in Energy and Xi'an:Xi'an Jiaotong University Press,2001.(in Chi- Combustion Science,2001,27(6):587-610. nese) [3]Jones J M,Pourkashanian M,Williams A,et al.A com- [8]Solomon P R,Hamblen D G,Carangelo R M,et al. prehensive biomass combustion model [J].Renewable General model of coal devolatilization[J].Energy Fu- Ener,2000,19(1):229-234. els,1988,2(4):405-422. [4]Donskoi E,McElwain D L S.Optimization of coal pyroly- [9]Niksa S,Lau C W.Global rates of devolatilization for va- sis modeling J].Combustion and Flame,2000,122 rious coal types[J].Combustion and Flame,1993,94: (3):359-367. 293-307. [5]Orfao JJ M.Review and evaluation of the approximations [10]Maki T,Takatsuno A,Miura K.Analysis of pyrolysis re- to the temperature integral[J].AIChE Journal,2007,53 actions of various coals including argonne premium coals (11):2905-2915. using a new distributed activation energy model[J].En- [6]胡国新,田伟学,许伟,等。大颗粒煤在移动床中的 erg&Fuels,1997,11(5):972-977. 热解模型[J].上海交通大学学报,2001,35(5):733- [11]Cai J M,Wu W X,Liu R H.An overview of distributed 736. activation energy model and its application in the pyrolysis Hu G X,Tian W X,Xu W,et al.Devolatilization model of lignocellulosic biomass[J].Renewable and Sustain- of large coal particles in moving bed [J].Journal of able Energy Reviews,2014,36:236-246. Shanghai Jiaotong University,2001,35(5):733-736. Approximation of the distributed activation energy model (DAEM) for computational fluid dynamics CFD)simulations of coal or biomass pyrolysis MA YiYa QI Juan ZHAO XinLei LIU Hui* (State Key Laboratory of Chemical Resource Engineering,College of Chemical Engineering,Beijing University of Chemical Technology, Beijing 100029,China) Abstract:The complex decomposition kinetics of coal or biomass is usually interpreted with the distributed activa- tion energy model (DAEM).However,when applied directly in computational models,this model is highly com- putationally intensive,because it requires multiple integrations at every time step for each computing grid.The present work proposes an approximation of the DAEM to make it more convenient to incorporate in computational model code.The method significantly reduces the computational time and cost.In addition,it affords the yield of pyrolysis products and the rate of production exactly.Furthermore,the model predictions fitted well with the experi- ment data for biomass and coal pyrolysis. Key words:biomass;coal;pyrolysis;distributed activation energy modeling http://www.journal.buct.edu.cn
formulations, solutions, evaluation, and application of comprehensive combustion models[J]. Progress in Ener鄄 gy and Combustion Science, 1999, 25(4): 387-436. [2] Williams A, Pourkashanian M, Jones J M. Combustion of pulverised coal and biomass[ J]. Progress in Energy and Combustion Science, 2001, 27(6): 587-610. [3] Jones J M, Pourkashanian M, Williams A, et al. A com鄄 prehensive biomass combustion model [ J ]. Renewable Energy, 2000, 19(1): 229-234. [4] Donskoi E, McElwain D L S. Optimization of coal pyroly鄄 sis modeling [ J ]. Combustion and Flame, 2000, 122 (3): 359-367. [5] 譫rf觔o J J M. Review and evaluation of the approximations to the temperature integral[J]. AIChE Journal, 2007, 53 (11): 2905-2915. [6] 胡国新, 田伟学, 许伟, 等. 大颗粒煤在移动床中的 热解模型[J]. 上海交通大学学报, 2001, 35(5): 733 - 736. Hu G X, Tian W X, Xu W, et al. Devolatilization model of large coal particles in moving bed [ J ]. Journal of Shanghai Jiaotong University, 2001, 35 (5): 733 -736. (in Chinese) [7] 邓建中, 刘之行. 计算方法[M]. 2 版. 西安: 西安交 通大学出版社, 2001. Deng J Z, Liu Z X. Computational method[M]. 2nd ed. Xi爷an: Xi爷an Jiaotong University Press, 2001. (in Chi鄄 nese) [8] Solomon P R, Hamblen D G, Carangelo R M, et al. General model of coal devolatilization[J]. Energy & Fu鄄 els, 1988, 2(4): 405-422. [9] Niksa S, Lau C W. Global rates of devolatilization for va鄄 rious coal types[ J]. Combustion and Flame, 1993, 94: 293-307. [10] Maki T, Takatsuno A, Miura K. Analysis of pyrolysis re鄄 actions of various coals including argonne premium coals using a new distributed activation energy model[ J]. En鄄 ergy & Fuels, 1997, 11(5): 972-977. [11] Cai J M, Wu W X, Liu R H. An overview of distributed activation energy model and its application in the pyrolysis of lignocellulosic biomass [ J]. Renewable and Sustain鄄 able Energy Reviews, 2014, 36: 236-246. Approximation of the distributed activation energy model (DAEM) for computational fluid dynamics (CFD) simulations of coal or biomass pyrolysis MA YiYa QI Juan ZHAO XinLei LIU Hui * (State Key Laboratory of Chemical Resource Engineering, College of Chemical Engineering, Beijing University of Chemical Technology, Beijing 100029, China) Abstract: The complex decomposition kinetics of coal or biomass is usually interpreted with the distributed activa鄄 tion energy model (DAEM). However, when applied directly in computational models, this model is highly com鄄 putationally intensive, because it requires multiple integrations at every time step for each computing grid. The present work proposes an approximation of the DAEM to make it more convenient to incorporate in computational model code. The method significantly reduces the computational time and cost. In addition, it affords the yield of pyrolysis products and the rate of production exactly. Furthermore, the model predictions fitted well with the experi鄄 ment data for biomass and coal pyrolysis. Key words: biomass; coal; pyrolysis; distributed activation energy modeling ·30· 北京化工大学学报(自然科学版) 2015 年 http://www.journal.buct.edu.cn