
第六章传热 6.1教学基本要求:(12学时) 传热过程加热和冷却方法:传热速率。 热传导傅利叶定律:常用工程材料的导热系数:一维导热的计算。 对流给热牛顿冷却定律:自然对流:管内强制对流(湍流)给热系数经验式:沸腾给热 和沸腾曲线:蒸汽冷凝给热 间壁换热过程热量衡算和传热速率式:传热平均温度差,热阻和传热系数:垢层热阻 传热计算传热设计型问题的参数选择和计算方法:传热操作型问题的讨论和计算。 换热器列管式换热器的设计与选型:常用换热器的结构。 6.2基本概念: 传热目的传热操作目的主要有①加热、冷却物料:②回收热量或冷量:③保温,减少 热量或冷量损失。 传热过程的三种基本方式直接接触式、间壁式、蓄热式。 载热体为将冷 工艺物料加热或热工艺物料冷却,必须用另一种流体供给或取走热量 此流体称为载热体。用于加热的称为加热剂:用于冷却的称为冷却剂。 三种传热机理的物理本质传导的物理本质是分子热运动、分子碰撞及自由电子迁移: 对流的物理本质是流动流体载热:热辐射的物理本质是电磁波。 间壁换热传热过程的三个步骤热量从热流体对流至壁面,经壁内热传导至另一侧,由 壁面对流至冷流体 导热系数物质的导热系数与物质的种类、物态、温度、压力有关。 热阻将传热速率表达成温差推动力除以阻力的形式,该阻力即为热阻 推动力高温物体向低温传热,两者的温度差就是推动力。 流动对传热的贡献流动流体载热 强制对流传热在人为造成强制流动条件下的对流传热。 自然对流传热因温差引起密度差,造成宏观流动条件下的对流传热。自然对流传热时 加热、冷却面的位置应该是加热面在下,制冷面在上,这样有利于形成充分的对流流动。 务塞尔数、普朗特数的物理意义 努塞尔数的物理意义是对流传热速率与导热传热速号 之比。普朗特数的物理意义是动量扩散系数与热量扩散系数之比,在α关联式中表示了物性 对传热的贡献。 ā关联式的宗性尺寸、定性温度用干确定关联式中的雷诺数第准数的长府变量、物州 数据的温度。比如,圆管内的强制对流传热,定性尺寸为管径、定性温度为进出口平均温 度。 大容积自然对流的自动模化区自然对流ā与高度1无关的区域。 液体沸避的两个必要条件热度W一ts、汽化核心 核状沸 汽泡依次产生和脱离加热面 对液休刷烈授动 4随 △t急刷上升 膜状沸腾 由于汽泡在脱离加热面之前就连接成汽膜,把加热面与液体隔开,使传热条 件变差。 临界点从核状沸腾变为膜状沸腾的转折点。 沸腾给热的强化改善加热表面,提供更多的汽化核心:沸腾液体加添加剂,降低表面 张力
46 第六章 传热 6.1 教学基本要求:(12 学时) 传热过程 加热和冷却方法;传热速率。 热传导 傅利叶定律;常用工程材料的导热系数;一维导热的计算。 对流给热 牛顿冷却定律;自然对流;管内强制对流(湍流)给热系数经验式;沸腾给热 和沸腾曲线;蒸汽冷凝给热。 间壁换热过程 热量衡算和传热速率式;传热平均温度差,热阻和传热系数;垢层热阻。 传热计算 传热设计型问题的参数选择和计算方法;传热操作型问题的讨论和计算。 换热器 列管式换热器的设计与选型;常用换热器的结构。 6.2 基本概念: 传热目的 传热操作目的主要有①加热、冷却物料;②回收热量或冷量;③保温,减少 热量或冷量损失。 传热过程的三种基本方式 直接接触式、间壁式、蓄热式。 载热体 为将冷工艺物料加热或热工艺物料冷却,必须用另一种流体供给或取走热量, 此流体称为载热体。用于加热的称为加热剂;用于冷却的称为冷却剂。 三种传热机理的物理本质 传导的物理本质是分子热运动、分子碰撞及自由电子迁移; 对流的物理本质是流动流体载热;热辐射的物理本质是电磁波。 间壁换热传热过程的三个步骤 热量从热流体对流至壁面,经壁内热传导至另一侧,由 壁面对流至冷流体。 导热系数 物质的导热系数与物质的种类、物态、温度、压力有关。 热阻 将传热速率表达成温差推动力除以阻力的形式,该阻力即为热阻。 推动力 高温物体向低温传热,两者的温度差就是推动力。 流动对传热的贡献 流动流体载热。 强制对流传热 在人为造成强制流动条件下的对流传热。 自然对流传热 因温差引起密度差,造成宏观流动条件下的对流传热。自然对流传热时, 加热、冷却面的位置应该是加热面在下,制冷面在上,这样有利于形成充分的对流流动。 努塞尔数、普朗特数的物理意义 努塞尔数的物理意义是对流传热速率与导热传热速率 之比。普朗特数的物理意义是动量扩散系数与热量扩散系数之比,在α关联式中表示了物性 对传热的贡献。 α关联式的定性尺寸、定性温度 用于确定关联式中的雷诺数等准数的长度变量、物性 数据的温度。比如,圆管内的强制对流传热,定性尺寸为管径 d、定性温度为进出口平均温 度。 大容积自然对流的自动模化区 自然对流α与高度 l 无关的区域。 液体沸腾的两个必要条件 过热度 tw-ts、汽化核心。 核状沸腾 汽泡依次产生和脱离加热面,对液体剧烈搅动,使α随Δt 急剧上升。 膜状沸腾 由于汽泡在脱离加热面之前就连接成汽膜,把加热面与液体隔开,使传热条 件变差。 临界点 从核状沸腾变为膜状沸腾的转折点。 沸腾给热的强化 改善加热表面,提供更多的汽化核心;沸腾液体加添加剂,降低表面 张力

蒸汽冷凝的两种形式滴状冷凝,膜状冷凝。工业传热按膜状冷凝计算,因为滴状冷凝 不能持久。 排放不凝性气体不凝性气体的存在,会降低蒸汽的压力,形成额外热阻。排放不凝性 气体的目的是避免其积累,提高ā。 黑体吸收率等于1的物体为黑体。 黑度实际物体辐射能力与同温度黑体的辐射能力之比。 对各种波长辐射能具有同样吸收率的理想物体 克希霍夫定律同一灰体的吸收率与其黑度在数值上相等,£=。 角系数仅与可见面积大小、角度、距离有关。 传热过程的控制步臻该步骤阻力远大于其他各步骤的阻力之和,传热速率由该步骤所 决定 传热操作线换热器同一横截面上热流体温度T与冷流体温度t的关系,它是换热器段 的热量衡算结果。 逆流、并流换热器中冷热流体相向而流称为逆流,同向而流称为并流。 6.3基本内容: 本章考察热传导、对流给热的传热速率,重点分析换热器的原理和设计、操作。 一、热传导 1.傅立叶定律 当物体存在温度差时就会发生热传导,热传导速率可以用傅立叶定律描述 9-1 6-1 式中入:Wm·℃,为导热系数。傅立叶定律表明,热流密度与温度梯度成正比。入的数量 级为:金属10-102Wm·℃: 绝热材料10210Wm·℃: 液体10Wm· 气体10W/m·C。 导热系数与物质的种类、物态、温度压力有关。其特点是: 1)入金属>入液体>入气体: 2)温度升高时,入下降,但水明显例外:入4上升:入属下降:大多入上升。 2.平壁导热 单层平壁在定态一维(横向导热不计)导热,且导热系数视作常数的条件下,对其进行解 析解分析:①取控制体②作热量衡算③结合特征方程解析解,可以导得: 热流量Q=,4-1=.-业 6-2 此式表明,温度在平壁中是线性分布的。上式也可表示为 6-3 式6-3的含义为 过程速率。推动力 阻力 6-4 对于多层平壁导热,由于每层壁过程速率相等,采用数学上的等比定律可得
47 蒸汽冷凝的两种形式 滴状冷凝,膜状冷凝。工业传热按膜状冷凝计算,因为滴状冷凝 不能持久。 排放不凝性气体 不凝性气体的存在,会降低蒸汽的压力,形成额外热阻。排放不凝性 气体的目的是避免其积累,提高α。 黑体 吸收率等于1的物体为黑体。 黑度 实际物体辐射能力与同温度黑体的辐射能力之比。 灰体 对各种波长辐射能具有同样吸收率的理想物体。 克希霍夫定律 同一灰体的吸收率与其黑度在数值上相等,ε=a。 角系数 仅与可见面积大小、角度、距离有关。 传热过程的控制步骤 该步骤阻力远大于其他各步骤的阻力之和,传热速率由该步骤所 决定。 传热操作线 换热器同一横截面上热流体温度 T 与冷流体温度 t 的关系,它是换热器段 的热量衡算结果。 逆流、并流 换热器中冷热流体相向而流称为逆流,同向而流称为并流。 6.3 基本内容: 本章考察热传导、对流给热的传热速率,重点分析换热器的原理和设计、操作。 一、热传导 1.傅立叶定律 当物体存在温度差时就会发生热传导,热传导速率可以用傅立叶定律描述 n t q ∂ ∂ = −λ 6-1 式中λ:W/m·℃,为导热系数。傅立叶定律表明,热流密度与温度梯度成正比。λ的数量 级为:金属 10~102 W/m·℃; 绝热材料 10-2~10-1W/m·℃; 液体 10-1W/m·℃; 气体 10-2W/m·℃。 导热系数与物质的种类、物态、温度压力有关。其特点是: 1)λ金属>λ液体>λ气体; 2)温度升高时,λ液下降,但水明显例外;λ气上升;λ金属下降;大多λ非金属上升。 2.平壁导热 单层平壁在定态一维(横向导热不计)导热,且导热系数视作常数的条件下,对其进行解 析解分析:①取控制体②作热量衡算③结合特征方程解析解,可以导得: 热流量 δ − = λ − = λ 1 1 2 t t A x t t Q A 6-2 此式表明,温度在平壁中是线性分布的。上式也可表示为 R t A t t Q ∆ = δ λ − = / 1 2 6-3 式 6-3 的含义为 阻力 推动力 过程速率 = 6-4 对于多层平壁导热,由于每层壁过程速率相等,采用数学上的等比定律可得

Q=-当-出+, R 6-5 R+R2 即串联过程推动力相加,阻力相加等式仍然成立,这是工程处理方法之一。式6-5还给出了 一个重要结果:温差按热阻大小分配,热阻大的温差也大。 例1己知:两层平壁入=1.4W/m·℃,6=100加m:入=0.14W/m·℃,6=200mm,两边的温度 为t,=650C,t,=50℃。平壁1在高温侧,平壁2在低温侧。 求:两壁接触处的温度: 解:先定性分析,哪个斜率大 热流密度9=--4 -650-50 0102=400m1m 1.40.14 由g=-得 0.2 2=50+400×014=621℃ 3.圆筒壁导热 圆筒壁导热经推导可得 6-6 In(/n) 2号 1-12△1_推动力 或写成通式:Q=2AR阻力 其中7圆简内的度分布不得是线的, 例2在蒸汽管道外包两层同样厚度的保温材料入,《入2,应将哪层包在里面? 解:将式6-6用于多层圆筒壁可得 入,包在里面 2π△ 1 入,包在里面 2πlM 2片入15 两种情况传热量不同,比较Q与Q,取小的。现比较分母,由于入〈入,所以
48 1 2 1 2 2 2 1 1 R R t t R t R t Q + ∆ + ∆ = ∆ = ∆ = 6-5 即串联过程推动力相加,阻力相加等式仍然成立,这是工程处理方法之一。式 6-5 还给出了 一个重要结果:温差按热阻大小分配,热阻大的温差也大。 例 1 已知:两层平壁λ1=1.4W/m·℃,δ1=100mm;λ2=0.14W/m·℃,δ2=200mm,两边的温度 为 t1=650℃,t3=50℃。平壁 1 在高温侧,平壁 2 在低温侧。 求:两壁接触处的温度 t2。 解:先定性分析,哪个斜率大 热流密度 2 2 1 1 1 3 λ δ + λ δ − = = t t A Q q 2 400 / 0.14 0.2 1.4 0.1 650 50 = W m + − = 由 2 2 2 3 λ δ − = t t q 得 0.14 0.2 50 400 2 2 2 3 = + × λ δ t = t + q = 621℃ 3.圆筒壁导热 圆筒壁导热经推导可得 ( ) ( ) 1 2 1 2 2 1 1 2 ln 2 ln / 1 2 r r L t t r r L t t Q π λ − = π λ − = 6-6 或写成通式: 阻力 推动力 = ∆ ∆ = δ λ − = R t A t t Q m / 1 2 其中: ( ) 2 1 2 1 ln A / A A A Am − = 。圆筒壁内的温度分布不再是线性的。 例 2 在蒸汽管道外包两层同样厚度的保温材料λ1<λ2,应将哪层包在里面? 解:将式 6-6 用于多层圆筒壁可得 λ1包在里面 2 3 1 2 2 1 1 ln 1 ln 1 2 r r r r l t Q λ + λ π ∆ = λ2包在里面 2 3 1 1 2 2 2 ln 1 ln 1 2 r r r r l t Q λ + λ π ∆ = 两种情况传热量不同,比较 Q1与 Q2,取小的。现比较分母,由于λ1<λ2,所以

(a) 由于>-82=(52+82-8)=r5 所以n ->0 由式(a)、b)可得 所以Q滑止 dy 1)两种对流形式 因温差引起密度差,造成宏观流动条件下的对流传热称为自然对流:在人为造成强制流 动条件下的对流传热称为强制对流。 2)牛顿冷却定律 流体与固体壁面之间的对流给热,可用牛顿冷却定律表达 q=a(T.-T) 6-7 其中:Tw:壁温:T:流体主体温度:a:给热系数W/m℃ 采用牛顺冷却定律来表达对流给热,便于分解组合传热系数 K。工业过程常采用间壁式换热器,热量从热流体对流至壁面,经 壁内热传导至另一侧,由壁面对流至冷流体。如图6.1所示。 由牛顿冷却定律和壁面导热,可得 入入2 q=a,(T-7n)=2红=a,n-0 图6.1传热步骤 或 g话---0 6-8 49
49 1 2 1 1 λ > λ (a) 由于 ( )( ) 2 2 2 2 2 2 2r > r − δ = r + δ r − δ 1 3 = rr 所以 ln 0 1 3 2 2 > rr r (b) 由式(a)、(b)可得 (ln ln ) 1 (ln ln ) 1 2 3 1 2 2 2 3 1 2 1 r r r r r r r r − λ − > λ 即 2 3 1 1 2 2 2 3 1 2 2 1 ln 1 ln 1 ln 1 ln 1 r r r r r r r r λ + λ > λ + λ 所以 Q1静止 qW 。 1)两种对流形式 因温差引起密度差,造成宏观流动条件下的对流传热称为自然对流;在人为造成强制流 动条件下的对流传热称为强制对流。 2)牛顿冷却定律 流体与固体壁面之间的对流给热,可用牛顿冷却定律表达 q (T T) = α w − 6-7 其中:Tw:壁温;T:流体主体温度;α:给热系数 W/m2 ℃。 采用牛顿冷却定律来表达对流给热,便于分解组合传热系数 K。工业过程常采用间壁式换热器,热量从热流体对流至壁面,经 壁内热传导至另一侧,由壁面对流至冷流体。如图6.1所示。 由牛顿冷却定律和壁面导热,可得 δ − = α − = λ W W W T t q (T T ) 1 ( ) 2 t t = α W − 图6.1 传热步骤 或 1 2 1/ / 1/α − = δ λ − = α − = T T T t t t q W W W W = K(T − t) 6-8

1 式中K=T8丁为传热系数。这样在不须知道,,的情况下,就可以计算热流密度 了. 3)a的影响因素 经分析,对流给热系数的影响为 a=fp,u,i1,u,βg,Cp 经无因次化之后,可得 兴=曾婴学 或 Nu=f(Re,Pr,Gr) 强制对流Nu=fRe,P) 自然对流u=f(Gr,Pr) 2.圆直管内强制湍流c 经实验数据关联获得,圆直管内强制湍流时的给热系数 Nu =0.023Re8 Pr 式中,当流体被加热时b=0.4:当流体被冷却时b=0.3。式6-9可写成 =0.023Re0s Pr -10 经验关联式6-10在应用时要注意: ①适用范围:Re>103,0.73040 ②定性温度:主体平均温度,即红+7)或北+h). ③定性尺寸:管径d。 影响因素分析: 6-11 即ā正比于流量的0.8次方,反比于管径的1.8次方。但是,流体流动阻力 6-12 d 说明减小管径、增大流速或流量都可提高,但是以机械能损失为代价 3.大容积自然对流a Nu=AGr.Pr)° 6-13
50 式中 1 2 1 1 1 α + λ δ + α K = 为传热系数。这样在不须知道TW,tW的情况下,就可以计算热流密度 了。 3)α的影响因素 经分析,对流给热系数的影响为 α = f (ρ,µ,λ,l,u,βg∆t,Cp) 经无因次化之后,可得 ( , , ) 2 3 2 µ β ∆ ρ λ µ µ ρ = λ α lu Cp g tl f l 或 Nu = f (Re,Pr,Gr) 强制对流 Nu = f (Re,Pr) 自然对流 Nu = f (Gr,Pr) 2.圆直管内强制湍流α 经实验数据关联获得,圆直管内强制湍流时的给热系数 b Nu 0.023Re Pr 0.8 = 6-9 式中,当流体被加热时 b=0.4;当流体被冷却时 b=0.3。式 6-9 可写成 b d 0.023 Re Pr λ 0.8 α湍 = 6-10 经验关联式 6-10 在应用时要注意: ①适用范围: 4 Re >10 ,0.7 30~40。 ②定性温度:主体平均温度,即 ( ) 2 1 T1 +T2 或 ( ) 2 1 1 2 t + t 。 ③定性尺寸:管径 d。 影响因素分析: 1.8 0.8 0.2 0.8 d q d u V α ∝ ∝ 6-11 即α正比于流量的 0.8 次方,反比于管径的 1.8 次方。但是,流体流动阻力 5 2 2 d q d u h V f ∝ ∝ 6-12 说明减小管径、增大流速或流量都可提高α,但是以机械能损失为代价。 3.大容积自然对流α b Nu = A(Gr⋅Pr) 6-13
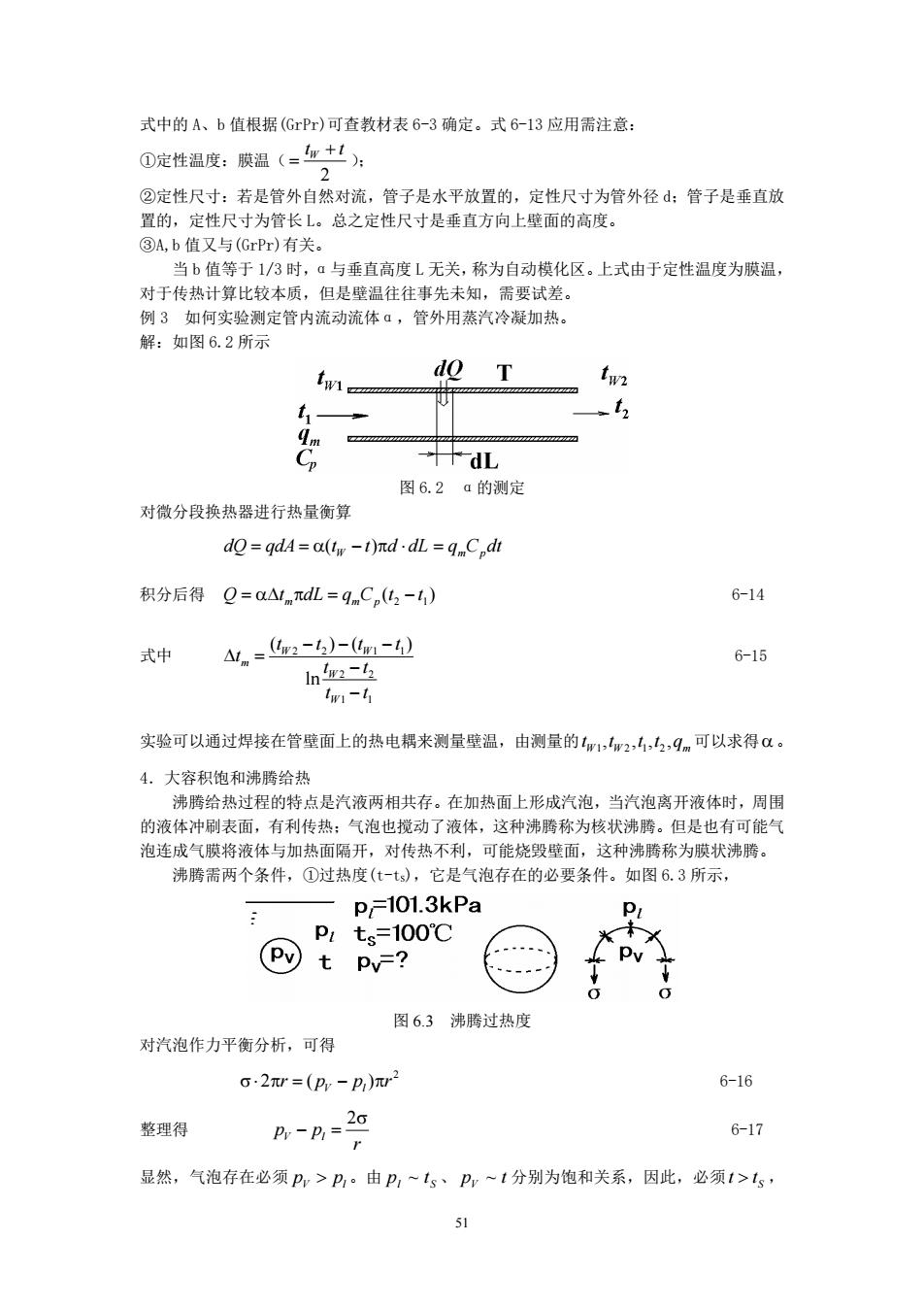
式中的A、b值根据(GrPr)可查教材表6-3确定。式6-13应用需注意: ①定性温度:膜温(=4,'), ②定性尺寸:若是管外自然对流,管子是水平放置的 定性尺寸为管外径d:管子是垂直放 置的,定性尺寸为管长L。总之定性尺寸是垂直方向上壁面的高度。 ③A,b值又与(GrPr)有关。 当b值等于1/3时,α与垂直高度L无关,称为自动模化区。上式由于定性温度为膜温, 对于传热计算出较本质,但是壁温往往事先未知,需要试差。 例3如何实验测定管内流动流体,管外用蒸汽冷凝加热 解:如图6.2所示 do T tw 十dL 图6.2a的测定 对微分段换热器进行热量衡算 dg=gdA=aum-1)πd·dL=qnC,dh 积分后得Q=a△mdL=qnC(凸-) 6-14 式中 出n=,-4)-m- 6-15 实验可以通过焊接在管壁面上的热电耦来测量壁温,由测量的11,2,4,2,qm可以求得α。 4.大容积饱和沸腾给热 沸腾给热过程的特点是汽液两相共存。在加热面上形成汽泡,当汽泡离开液体时,周围 的液体冲刷表面,有利传热:气泡也搅动了液体,这种沸腾称为核状沸腾。但是也有可能气 泡连成气膜将 液体与加热面隔开,对传热不利, 可能烧毁壁面 这种沸腾称为膜状沸腾 沸腾需两个条件,①过热度(t-t),它是气泡存在的必要条件。如图63所示, P/=101.3kPa P P1ts=100℃ (Pv) t py=? 6 图63沸腾过热度 对汽泡作力平衡分析,可得 2w=(p-p,)r2 6-16 整理得 BB=20 6-17 显然,气泡存在必须P>P,。由P,~1。、pp~1分别为饱和关系,因此,必须1>1, 51
51 式中的 A、b 值根据(GrPr)可查教材表 6-3 确定。式 6-13 应用需注意: ①定性温度:膜温( 2 t t W + = ); ②定性尺寸:若是管外自然对流,管子是水平放置的,定性尺寸为管外径 d;管子是垂直放 置的,定性尺寸为管长 L。总之定性尺寸是垂直方向上壁面的高度。 ③A,b 值又与(GrPr)有关。 当 b 值等于 1/3 时,α与垂直高度 L 无关,称为自动模化区。上式由于定性温度为膜温, 对于传热计算比较本质,但是壁温往往事先未知,需要试差。 例 3 如何实验测定管内流动流体α,管外用蒸汽冷凝加热。 解:如图 6.2 所示 图 6.2 α的测定 对微分段换热器进行热量衡算 dQ = qdA = α(t W − t)πd ⋅ dL q C dt = m p 积分后得 ( ) 2 1 Q t dL q C t t = α∆ mπ = m p − 6-14 式中 1 1 2 2 2 2 1 1 ln ( ) ( ) t t t t t t t t t W W W W m − − − − − ∆ = 6-15 实验可以通过焊接在管壁面上的热电耦来测量壁温,由测量的 W W qm t ,t ,t ,t , 1 2 1 2 可以求得α 。 4.大容积饱和沸腾给热 沸腾给热过程的特点是汽液两相共存。在加热面上形成汽泡,当汽泡离开液体时,周围 的液体冲刷表面,有利传热;气泡也搅动了液体,这种沸腾称为核状沸腾。但是也有可能气 泡连成气膜将液体与加热面隔开,对传热不利,可能烧毁壁面,这种沸腾称为膜状沸腾。 沸腾需两个条件,①过热度(t-tS),它是气泡存在的必要条件。如图 6.3 所示, 图 6.3 沸腾过热度 对汽泡作力平衡分析,可得 2 2 r ( p p ) r σ⋅ π = V − l π 6-16 整理得 r pV pl σ − = 2 6-17 显然,气泡存在必须 pV > pl 。由 l S p ~ t 、 p t V ~ 分别为饱和关系,因此,必须 S t > t

也就是要有一定的过热度。究竟△p引起多少△,可以由克莱普龙方程计算。 ②汽化核心,它是气泡生成的必要条件。由式6-17可知, 越小 ,压差越大 ,所需过 热度也越大。所以,粗糙表面所需过热度小:光滑表面所需过热度大,基至会发生暴沸。 例如,加沸石的作用就是提供汽化核心,防止暴沸。 膜状沸腾 核状沸腾个 lga 不稳定 工业操作区 临界点 辐射 传热 表面汽化 lg△t 图6.4 沸腾给热系数 由图6.4所示的沸腾曲线可见,随着过热度的增加,起先是表面汽化阶段,然后是核状 沸腾:汽泡依次产生并脱离加热面,对液体制烈搅动,使α随△t急剧上升:过热度再大就 进入膜状沸腾,汽泡在脱离加热面之前就连接成汽膜,把加热面与液体隔开,使传热条件变 差。工业操作只能在核状沸腾区域进行,因为膜状沸腾会造成飞温和烧毁炉壁等危险。 沸腾过程的强化可以从沸腾的条件入手,①加热表 面粗糙化,增强汽化核心:②加入添 加剂,降低表面张力。 5.蒸汽冷凝给热 1)膜状冷凝与滴状冷凝 蒸汽在冷壁上冷凝有两种方式,即膜状冷凝与滴状冷凝。滴状冷凝的给热系数比膜 冷凝的大50倍。但是,在工业上,滴状冷凝不能持久, 设计按膜状冷凝考虑。 2)垂直液膜层流的平均 垂直壁液膜层流时的平均α冷经数学推导和实验测定为: 6-18 △1=T一Tm,即饱和蒸汽温度与冷壁温度之差。L为垂直壁高度。由 B 式6-18可见,冷凝给热系数a与温差△t有关。 3)水平圆管外液膜层流的α济题: a*=072pg呢7内 6-19 udo△ 在使用式6-18、19时,要注意:①物性p、μ、入是凝液的,而不是 燕汽的,因为热阻主要在液膜。②Re<2000,Re的确定。如图6.5所示 的垂直平壁,当量直径d.= 4A ,质量流速G=9,则 图6.5冷凝给热 Re=dG_4qm 6-20 u Iu 对于垂直圆管外Ⅱ=πd。:水平圆管外Ⅱ=管长L。③定性温度:膜温化、+1)。④特性
52 也就是要有一定的过热度。究竟 ∆p 引起多少 ∆t ,可以由克莱普龙方程计算。 ②汽化核心,它是气泡生成的必要条件。由式 6-17 可知,r 越小,压差越大,所需过 热度也越大。所以,粗糙表面所需过热度小; 光滑表面所需过热度大,甚至会发生暴沸。 例如,加沸石的作用就是提供汽化核心,防止暴沸。 图 6.4 沸腾给热系数 由图 6.4 所示的沸腾曲线可见,随着过热度的增加,起先是表面汽化阶段,然后是核状 沸腾:汽泡依次产生并脱离加热面,对液体剧烈搅动,使α随Δt 急剧上升;过热度再大就 进入膜状沸腾,汽泡在脱离加热面之前就连接成汽膜,把加热面与液体隔开,使传热条件变 差。工业操作只能在核状沸腾区域进行,因为膜状沸腾会造成飞温和烧毁炉壁等危险。 沸腾过程的强化可以从沸腾的条件入手,①加热表面粗糙化,增强汽化核心;②加入添 加剂,降低表面张力。 5.蒸汽冷凝给热 1)膜状冷凝与滴状冷凝 蒸汽在冷壁上冷凝有两种方式,即膜状冷凝与滴状冷凝。滴状冷凝的给热系数比膜状 冷凝的大 5~10 倍。但是,在工业上,滴状冷凝不能持久,设计按膜状冷凝考虑。 2)垂直壁液膜层流的平均α冷凝 垂直壁液膜层流时的平均α冷凝经数学推导和实验测定为: 4 1 2 3 1.13 µ ∆ ρ λ α = L t gr 垂直 6-18 TS TW ∆t = − ,即饱和蒸汽温度与冷壁温度之差。L 为垂直壁高度。由 式 6-18 可见,冷凝给热系数α与温差Δt 有关。 3)水平圆管外液膜层流的α冷凝: 4 1 0 2 3 0.725 µ ∆ ρ λ α = d t gr 水平 6-19 在使用式 6-18、19 时,要注意:①物性ρ、μ、λ是凝液的,而不是 蒸汽的,因为热阻主要在液膜。②Re<2000,Re 的确定。如图 6.5 所示 的垂直平壁,当量直径 Π = A de 4 ,质量流速 A q G m = ,则 图 6.5 冷凝给热 Πµ = µ = deG 4qm Re 6-20 对于垂直圆管外Π = πd0 ;水平圆管外Π =管长 L。③定性温度:膜温 ( ) 2 1 S W t + t 。④特性

尺寸:垂直管外L:水平管外d:水平管束外为nd。 管外冷凝,管子水平放还是垂直放好。由式6-18、19相比,可得 a赶=0.645 6-21 Q垂直 do 当L/>5.9时,a水平>a套直。显然,水平放比垂直放要好。 4)不凝性气体的影响 当蒸汽中存在不凝性气体时,在冷凝膜附近的蒸汽分压降低,有一个附加的惰性气体层, 蒸汽必须扩散通过该层惰性气体层,增加了额外的热阻。因此,必须定期排放不凝性气体, 减小蒸汽给热热阻。 例4若传热温差推动力增加一倍,试求下列条件下传热速率是原来的多少倍? 圆管内强制湍流 ②大容积自然对流 ③大容积饱和核状沸腾: ④蒸汽膜状冷凝。 解:0a=0.023RePr0 a与无关,4-a-2 ac△t ②&xA号 4-=218-252 q△1 ③ax△r25 号-”-3 国acy 号-微-16 通常,a的大小顺序如下: a气,自然对流 5-10w/am2℃ a气,强制对流 10-100W/m2℃ a液,自然对流 50-1000Wm 27 a液,强制对流 ā蒸汽冷裙 103-3×10W/m2℃ a液体沸腾 103-6×10wm2℃
53 尺寸: 垂直管外 L;水平管外 d0;水平管束外为 nd0。 管外冷凝,管子水平放还是垂直放好。由式 6-18、19 相比,可得 4 1 0.64( ) d0 L = α α 垂直 水平 6-21 当 L/d>5.9 时,α水平 > α垂直 。显然,水平放比垂直放要好。 4)不凝性气体的影响 当蒸汽中存在不凝性气体时,在冷凝膜附近的蒸汽分压降低,有一个附加的惰性气体层, 蒸汽必须扩散通过该层惰性气体层,增加了额外的热阻。因此,必须定期排放不凝性气体, 减小蒸汽给热热阻。 例 4 若传热温差推动力增加一倍,试求下列条件下传热速率是原来的多少倍? ①圆管内强制湍流; ②大容积自然对流; ③大容积饱和核状沸腾; ④蒸汽膜状冷凝。 解:① 0.8 0.3~0.4 0.023 Re Pr d λ α = α 与 ∆t 无关, 2 ' ' ' = α∆ α ∆ = t t q q ② 3 1 ~ 8 1 α ∝ ∆t 2.18 ~ 2.52 ' ' ' = α∆ α ∆ = t t q q ③ 2.5 α ∝ ∆t 11.3 ' ' 3.5 = ∆ ∆ = t t q q ④ 4 1 − α ∝ ∆t 1.68 ' ' 4 3 = ∆ ∆ = t t q q 通常,α的大小顺序如下: α气,自然对流 5~10 W/m2 ℃ α气,强制对流 10~100 W/m2 ℃ α液,自然对流 50~1000 W/m2 ℃ α液,强制对流 500~104 W/m2 ℃ α蒸汽冷凝 103 ~3×104 W/m2 ℃ α液体沸腾 103 ~6×104 W/m2 ℃

三、换热过程计算 1传热速率和传热系 对图6.6所示的换热器进行分析, m2冷流体 热流体 片t2 传热面积A 图6.6换热器分析 在定态条件下,Q级类不计,冷、热流体无相变化,9Cp1,9Cp2,K沿传热面不变,有 qmCpl(T-T)=qm2Cp2(t2-4) 6-22 过程特征方程 q==KT-) 6-23 dA 取其中的微元L长度进行考察 内侧微元面积 dA nddl 外侧微元面积 d4=πd2dl 管壁导热微元面积dAn=πd.·d机 0=g-T-=4-=Kd4-0=Kd4(- 1 adh AdA ad 注意:推动力、系数、面积的配套。当以内壁面为基准时,有 K+84+可 6-24 a7d a:da 以外壁面为基准(较常用) 1 K,=1d2842+ 6-25 实际考虑两侧污垢: K,= 6-26 1 a 只省平有=名=水,政只古+民+受尼+ CL
54 三、换热过程计算 1.传热速率和传热系数 对图 6.6 所示的换热器进行分析, 图 6.6 换热器分析 在定态条件下,Q损失 不计,冷、热流体无相变化, qm1Cp1,qm2Cp2 ,K 沿传热面不变,有 ( ) ( ) 1 1 1 2 2 2 2 1 q C T T q C t t m p − = m p − 6-22 过程特征方程 K(T t) dA dQ q = = − 6-23 取其中的微元 dL 长度进行考察 内侧微元面积 dA1 = πd1 ⋅ dL 外侧微元面积 dA2 = πd2 ⋅ dL 管壁导热微元面积 dAm = πdm ⋅ dL dQ = qdA 1 1 2 2 1 1 dA t t dA T t dA T T w m w w w α − = λ δ − = α − = ( ) 1 1 = K dA T − t ( ) 2 2 = K dA T − t 注意:推动力、系数、面积的配套。当以内壁面为基准时,有 2 1 2 1 1 1 1 1 1 d d d d K m α + λ δ + α = 6-24 以外壁面为基准(较常用) 2 2 1 2 1 2 1 1 1 α + λ δ + α = dm d d d K 6-25 实际考虑两侧污垢: 2 2 2 1 2 1 1 2 1 ) 1 ( 1 α + + λ δ + + α = R d d d d R K m 6-26 只有平壁才有 K1 = K2 = K ,或 2 1 2 1 1 1 1 α + + λ δ + + α = R R K

2.传热阻力控制问题 新管子,或经除垢后的管子,R=R=0。通常入较大,壁8薄,如入w=45m/m·K,取6 =1.5mm,/8=3×10/mK,与另外两项相比较,可取6/入≈0,则: 1-11 6-27 K a a2 从上式可以得出①K比a、a,中较小的一个a还小:②当a>》a2,则K≈a,强化传热须 从a小的一侧入手:③壁温计算:由于8/入≈0,T=t q=a,(T-T)=2(n-0 6-28 结论:壁温总是接近α值大的一边流体温度。壁温计算可用下式 1 T-Ts-1+ 6-29 T-t a d2 例5α值对K的影响 无污垢时, 11,1 K/K原 原值 20 50019.2 a1加倍 40500 37.0 1.93 a2加倍 20100019.6 1.02 上述计算说明,K是由较小的ā一侧所控制的。 例6用蒸汽加热冷物料,物料进口温度为20℃,出口温度为50℃,蒸汽温度为140℃,物料 侧给热系数α,=1000W/m2℃,蒸汽一侧α,=10/m2℃,求:平均壁温.(金属壁热阻可忽略) 解:物料平均温度为 1=20+50=35℃ 2 由式6-29 140 -Iw 104 140-3510++10 得t130.5℃。 3.传热过程基本方程式 对换热器数学描述后,可得到: Q=g.9(-=9,9.-=K4-)--2-K. In -6 6-30 T2-41
55 2.传热阻力控制问题 新管子,或经除垢后的管子,R1=R2=0。通常λ金属较大,壁δ薄,如λ钢=45W/m·K,取δ =1.5mm,λ/δ=3×104 W/m2 ·K,与另外两项相比较,可取δ/λ≈0,则: 1 2 1 1 1 α + α = K 6-27 从上式可以得出①K 比α1、α2中较小的一个α还小;②当α1>>α2,则 K≈α2,强化传热须 从α小的一侧入手;③壁温计算:由于δ/λ≈0,TW=tW ( ) ( ) 1 2 q T T t t = α − w = α w − 6-28 结论:壁温总是接近α值大的一边流体温度。壁温计算可用下式 1 2 1 1 1 1 α + α α = − − T t T TW 6-29 例 5 α 值对 K 的影响 无污垢时, 1 2 1 1 1 α + α = K α1 α2 K K / K原 原值 20 500 19.2 α1 加倍 40 500 37.0 1.93 α2 加倍 20 1000 19.6 1.02 上述计算说明,K 是由较小的α一侧所控制的。 例 6 用蒸汽加热冷物料,物料进口温度为 20℃,出口温度为 50℃,蒸汽温度为 140℃,物料 一侧给热系数α2 =1000W/m2 ℃,蒸汽一侧α1 =104 W/m2 ℃,求:平均壁温.(金属壁热阻可忽略) 解:物料平均温度为 35 2 20 50 = + t = ℃ 由式 6-29 4 3 4 10 10 10 140 35 140 − − − + = − − Wt 得 tW=130.5℃。 3.传热过程基本方程式 对换热器数学描述后,可得到: ( ) ( ) 1 1 1 2 2 2 1 2 Q q Cp T T q Cp t t = m − = m − m KA t T t T t T t T t KA = ∆ − − − − − = 2 1 1 2 1 2 2 1 ln ( ) ( ) 6-30