
4.Asymptotic Spectrum Theorems 1
1 4. Asymptotic Spectrum Theorems

Overview An other case for spectrum sensing Asymptotic moment method Central limit theorem 2
2 Overview • An other case for spectrum sensing • Asymptotic moment method • Central limit theorem

4.2.4 Asymptotic Spectral Distributions for Hermitian Matrix Recall the content of last class MP MP a b b b The Marchenko-Pastur support The Marchenko-Pastur support plus a signal component H otherwise
4.2.4 Asymptotic Spectral Distributions for Hermitian Matrix Recall the content of last class 2 max 0 2 min 1 1 , 1 , H if decision H otherwise The Marchenko-Pastur support The Marchenko-Pastur support plus a signal component

4.2.4 Asymptotic Spectral Distributions for Hermitian Matrix Theorem 4.2.7.Assume that the noise is complex,and n~N(0,1) /3 Let(网and-人r+W风+灰We have 入n(R)-L→Fa-witm where R=YY and Tiom is Tracy-Widom distribution of order 2 -0.36 -0.18 -0.12 -0.08 1.98 2.13 2.76 3.85 F2() 0.01 0.10 0.15 0.2 0.85 0.90 0.95 0.99
4.2.4 Asymptotic Spectral Distributions for Hermitian Matrix Theorem 4.2.7 . Assume that the noise is complex, and 2 = + N K and 1/3 1 1 v N K + N K . We have max 2 ( ) Tracy widom F v R where † R YY 2 Tracy widom F and is Tracy-Widom distribution of order 2 t -0.36 -0.18 -0.12 -0.08 … 1.98 2.13 2.76 3.85 F2 (t) 0.01 0.10 0.15 0.2 … 0.85 0.90 0.95 0.99 n ~ (0,1) ij N Let

4.2.4 Asymptotic Spectral Distributions for Hermitian Matrix Also,we define a decision value as follow Ho2 入m∠Y decision 入nin H otherwise For the false alarm P,we have P。=P>Y1H =P(入na(R)>Yin =P(max(R)>YNAmin) =P(入mx(R)>y(WN-√K)) 2- 1-F Y(N-R)-m 5
5 4.2.4 Asymptotic Spectral Distributions for Hermitian Matrix max 0 min 1 , , H if decision H otherwise Also, we define a decision value as follow max 0 min max min max min 2 max 2 max 2 2 | 1 ( ) ( ) = ( ) ( ) 1 P P H fa P N P N P N K N K P v v N K F v R R R R For the false alarm , we have Pfa

4.2.4 Asymptotic Spectral Distributions for Hermitian Matrix Hence,we have ↓ 丽--u--P And finally,we have F(1-Pa)v (N-)-u 6
6 4.2.4 Asymptotic Spectral Distributions for Hermitian Matrix Hence,we have 2 2 1 fa N K F P v 2 1 2 1 fa N K F P v And finally, we have 1 2 2 1 F P v fa N K
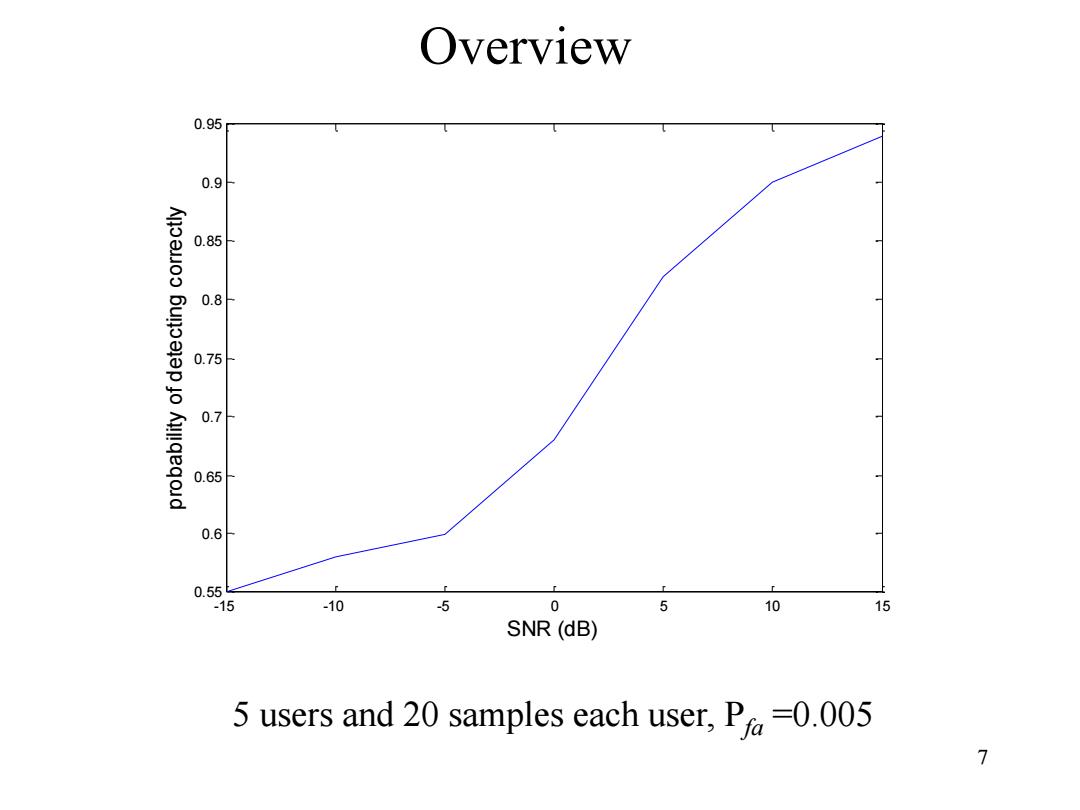
Overview 0.95 0.9 0.85 0.8 0.75 0.7 0.65 0.6 0.55 -15 -10 5 0 5 10 15 SNR(dB) 5 users and 20 samples each user,P=0.005 7
7 Overview -15 -10 -5 0 5 10 15 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 SNR (dB) probability of detecting correctly 5 users and 20 samples each user, Pfa =0.005

4.3.Asymptotic Moment Method Definition:In asymptotic regime,H is an NXK matrix,we denote the empirical distribution of HHH as fx),and the i-th moment of fx) is defined as rar天] where [a,b]is domain of fx). Theorem 4.2.4.Consider an NXK matrix H whose entries are independent zero-mean complex (or real)random variables with variance 1/N and fourth moments of order O(1/N2 )As K,N->co with N./K→B,we have 安→以jr 8
8 4.3. Asymptotic Moment Method Theorem 4.2.4. Consider an N×K matrix H whose entries are independent zero-mean complex (or real) random variables with variance 1/N and fourth moments of order O( 1/N2 ). As K,N → ∞ with N/K→ β, we have Definition: In asymptotic regime, H is an N×K matrix, we denote the empirical distribution of HHH as f(x), and the i-th moment of f(x) is defined as 1 H ( )d lim b i i a K x f x x tr K H H 1 H 0 1 1 1 i i k k i i tr K i k k H H where [a,b] is domain of f(x)

4.3.Asymptotic Spectral Distributions for Hermitian Matrix Example 4.3.5:MMSE detector with low complexity Consider the following communication channel y=Hd+n with d=ddC"some transmitted vectorial data of dimension n,assumed to have zero mean and covariance matrix n,nCN is an additive Gaussian noise vector of zero mean and covarianceI,y=CNis the reccived signal,and HCNx"is the multi-dimensional communication channel. 9
9 4.3. Asymptotic Spectral Distributions for Hermitian Matrix Consider the following communication channel with some transmitted vectorial data of dimension , assumed to have zero mean and covariance matrix In , is an additive Gaussian noise vector of zero mean and covariance IN , is the received signal, and is the multi-dimensional communication channel. y Hd n T 1 ,..., n n d d d n N n T 1 ,..., N n y y y N n H Example 4.3.5:MMSE detector with low complexity 2

4.3.Asymptotic Spectral Distributions for Hermitian matrix Under these model assumptions,irrespective of the communication scenario under study(e.g.MIMO,CDMA),the minimum mean square error decoder output for the vector x reads: =(H"H+G2IH"y =H"(H+o21w))厂y For practical applications,recovering therefore requires the inversion of the potentially large (HHH+021)matrix. 10
10 4.3. Asymptotic Spectral Distributions for Hermitian Matrix Under these model assumptions, irrespective of the communication scenario under study(e.g. MIMO, CDMA), the minimum mean square error decoder output for the vector x reads: For practical applications, recovering therefore requires the inversion of the potentially large (HHH+σ2 In ) -1 matrix. x ˆ 1 H 2 H 1 H H 2 ˆ n N x H Η I H y H ΗH I y x ˆ