
4.Asymptotic Spectrum Theorems 1
1 4. Asymptotic Spectrum Theorems

Overview We will talk asymptotic spectral distributions such as: ·Semicircle law ·Circular law Marcenko-Pastur law (MP law) ·Quarter circle law 。Ring law 2
Overview 2 We will talk asymptotic spectral distributions such as: • Semicircle law • Circular law • Marcenko-Pastur law (MP law) • Quarter circle law • Ring law

4.1.Why go to infinity The limiting results for infinite dimension matrices are very simple and explicit Apply the limiting results into the analysis of large matrices in realistic applications This approximate method is often stunningly precise and even sometimes can be applied to approximate scenarios where the dimension of the matrix is very small. 3
3 4.1. Why go to infinity ? • The limiting results for infinite dimension matrices are very simple and explicit • Apply the limiting results into the analysis of large matrices in realistic applications • This approximate method is often stunningly precise and even sometimes can be applied to approximate scenarios where the dimension of the matrix is very small

4.2.Asymptotic Spectral Distributions Definition:The empirical spectral distribution function (e.d.f)of the eigenvalues of an n xn Hermitian matrix A is denoted by F defined as 贸)=∑1(A)≤x刘 i=1 where,(A),···,n(A)are the eigenvalues of A and 1{}is the indicator function. If F converges as n->o,then the corresponding limit (asymptotic empirical distribution or asymptotic spectrum)is simply denoted by FA(x). 4
4 4.2. Asymptotic Spectral Distributions Definition: The empirical spectral distribution function (e.d.f) of the eigenvalues of an n × n Hermitian matrix A is denoted by defined as 1 1 F ( ) 1 ( ) n n i i x x n A A F n A where λ1 (A), . . . , λn (A) are the eigenvalues of A and 1{·} is the indicator function. If converges as n→∞, then the corresponding limit (asymptotic empirical distribution or asymptotic spectrum) is simply denoted by FA (x). F n A

4.2.1 Asymptotic Spectral Distributions for Wigner matrix Theorem 4.2.1 Consider an NXN standard Wigner matrix W such that,for some constant K,and sufficiently large N msw门 Then,the empirical spectral distribution of W converges almost surely to the semicircle law [1]whose density is w()=V4- 2π with x≤2. [1]E.Wigner,On the distribution of the roots of certain symmetric matrices [J], Annals Math.,1958,67,325-327
5 4.2.1 Asymptotic Spectral Distributions for Wigner matrix Theorem 4.2.1 Consider an N×N standard Wigner matrix W such that, for some constant κ, and sufficiently large N 4 , 2 1 max i j i j N N W Then, the empirical spectral distribution of W converges almost surely to the semicircle law [1] whose density is 1 2 ( ) 4 2 w x x with |x| ≤ 2. [1] E. Wigner,On the distribution of the roots of certain symmetric matrices[J], Annals Math.,1958,67,325 - 327.

4.2.1 Asymptotic Spectral Distributions for Wigner matrix 0.31 0.25H 0.2 0.15 0.1 0.05 The semicircle law compared with the histogram of the average of 100 empirical density functions for a Wigner matrix of size n=100. 6
6 4.2.1 Asymptotic Spectral Distributions for Wigner matrix The semicircle law compared with the histogram of the average of 100 empirical density functions for a Wigner matrix of size n = 100

4.2.2 Asymptotic Spectral Distributions for Square Matrix Theorem 4.2.2.Let H be an N X N complex random matrix whose entries a are independent random variables with identical mean, variance 1/N and finite kth moments for k 4.Then,the asymptotic spectrum of H converges almost surely to the circular law [2],namely the uniform distribution over the unit disk on the complex plane {5∈C:g≤1 whose density is given by 无(传)-1 兀 [2]V.L.Girko,Circular Law [J],Theory Prob.Appl.,1984,29,647-709
7 4.2.2 Asymptotic Spectral Distributions for Square Matrix Theorem 4.2.2. Let H be an N × N complex random matrix whose entries are independent random variables with identical mean, variance 1/N and finite kth moments for k ≥ 4. Then, the asymptotic spectrum of H converges almost surely to the circular law [2], namely the uniform distribution over the unit disk on the complex plane whose density is given by 1 ( ) C f { : 1} [2] V. L.Girko, Circular Law [J],Theory Prob. Appl.,1984,29,647 - 709.

4.2.2 Asymptotic Spectral Distributions for Square Matrix 15 0.5 0 -0.5 -1 -1 -0.5 0 05 1 1.5 The full-circle law and the eigenvalues of a realization of a matrix of size n=500 8
8 4.2.2 Asymptotic Spectral Distributions for Square Matrix The full-circle law and the eigenvalues of a realization of a matrix of size n = 500

4.2.3 Asymptotic Spectral Distributions for Product of Non-Hermitian Matrices Theorem 4.2.4.Consider an NXK (N>K)matrix H whose entries are independent zero-mean complex (or real)random variables with variance 1/N.As K,N-oo with KN->B.The product of non-Hermitian random matrices is defined as z=ΠX where X,is the singular value equivalent of Hie.x,=UH,where U is an unitary matrix.The empirical eigenvalue distribution of Z converge almost surely to the limit given by: o-- elsewhere This is called ring law. 9
9 4.2.3 Asymptotic Spectral Distributions for Product of Non-Hermitian Matrices Theorem 4.2.4. Consider an N×K (N>K) matrix H whose entries are independent zero-mean complex (or real) random variables with variance 1/N. As K,N → ∞ with K/N→ β. The product of non-Hermitian random matrices is defined as where Xi is the singular value equivalent of Hi , .i.e. where U is an unitary matrix. The empirical eigenvalue distribution of Z converge almost surely to the limit given by: 1 a i i Z X 1 1 2/ 2 / 2 1 1 (z) 0 a i i a a z z f a elsewhere X † X U H H i i i This is called ring law
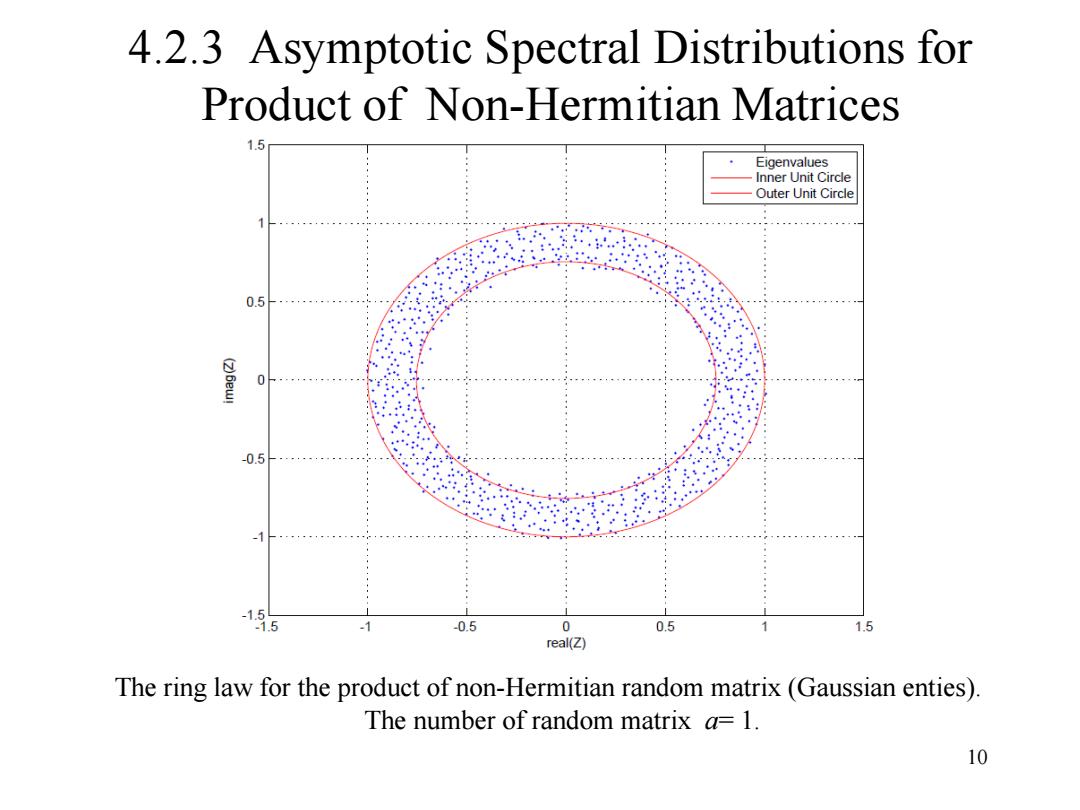
4.2.3 Asymptotic Spectral Distributions for Product of Non-Hermitian Matrices 1.5 Eigenvalues Inner Unit Circle Outer Unit Circle 0.5 0 1. ,1 -0.5 -1 -1.5 1.5 -0.5 0 0.5 1.5 real(Z) The ring law for the product of non-Hermitian random matrix(Gaussian enties). The number of random matrix a=1. 10
10 4.2.3 Asymptotic Spectral Distributions for Product of Non-Hermitian Matrices The ring law for the product of non-Hermitian random matrix (Gaussian enties). The number of random matrix a= 1