
7 Analysis of neural networks: a random matrix approach The inherent intractability of neural network performances,which mainly originates from the non linearity of the neural activations (as well as from learning by back-propagation of the error). With this observation in mind,we propose here a theoretical study of the performance of large dimensional neural networks (in the sense of large datasets and number of neurons)
The inherent intractability of neural network performances, which mainly originates from the non linearity of the neural activations (as well as from learning by back-propagation of the error). 7 Analysis of neural networks: a random matrix approach With this observation in mind, we propose here a theoretical study of the performance of large dimensional neural networks (in the sense of large datasets and number of neurons)
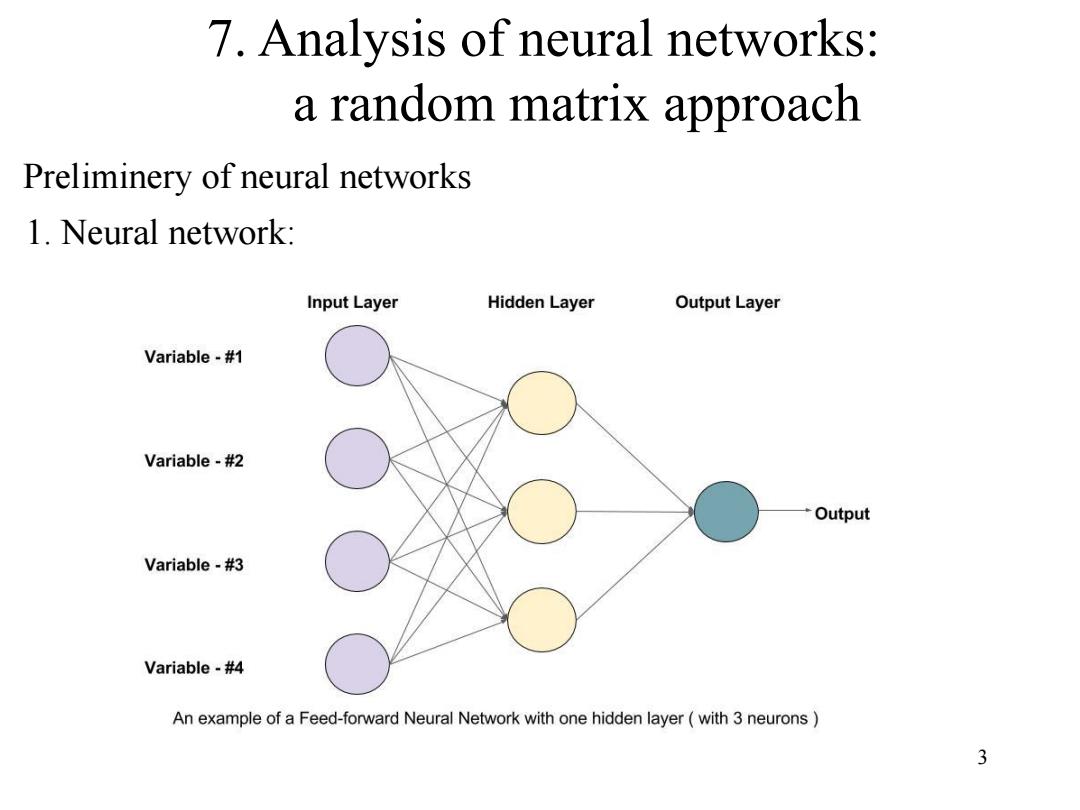
7.Analysis of neural networks: a random matrix approach Preliminery of neural networks 1.Neural network: Input Layer Hidden Layer Output Layer Variable-#1 Variable-#2 Output Variable-#3 Variable-#4 An example of a Feed-forward Neural Network with one hidden layer(with 3 neurons 3
3 7. Analysis of neural networks: a random matrix approach Preliminery of neural networks 1. Neural network:
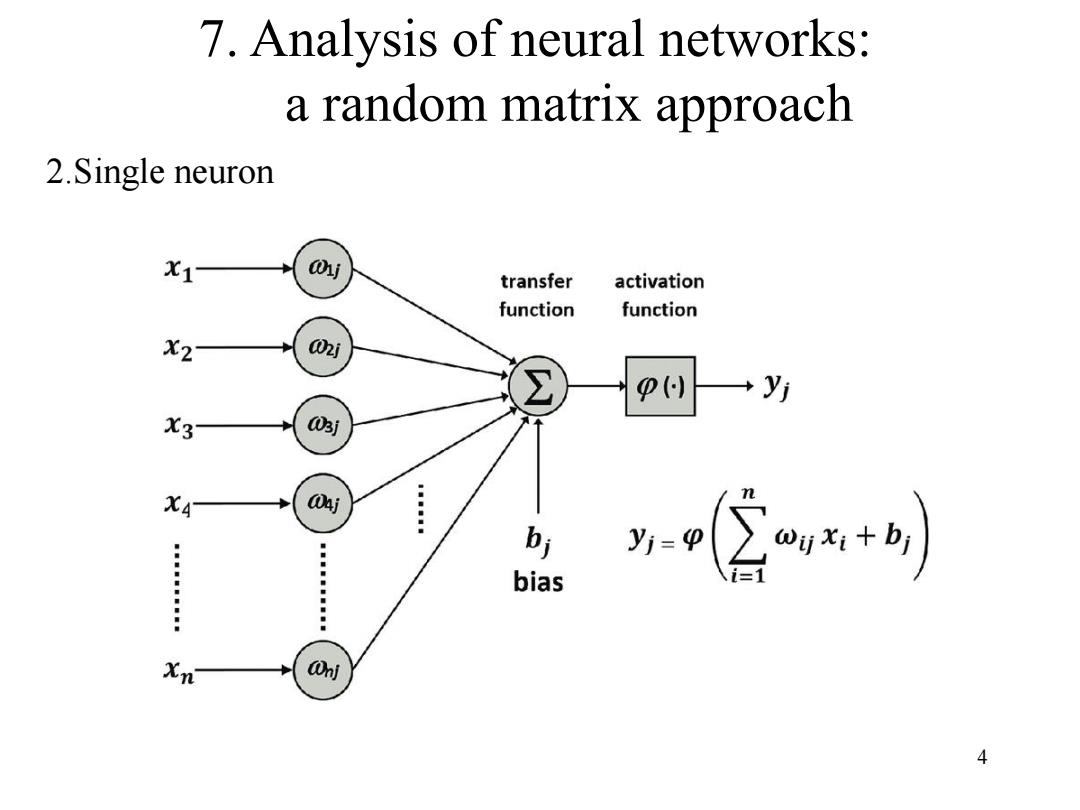
7.Analysis of neural networks: a random matrix approach 2.Single neuron x1 j transfer activation function function X2 02j P() X3 03j XA 04j bi bias y公+ Xn Onj 4
4 7. Analysis of neural networks: a random matrix approach 2.Single neuron
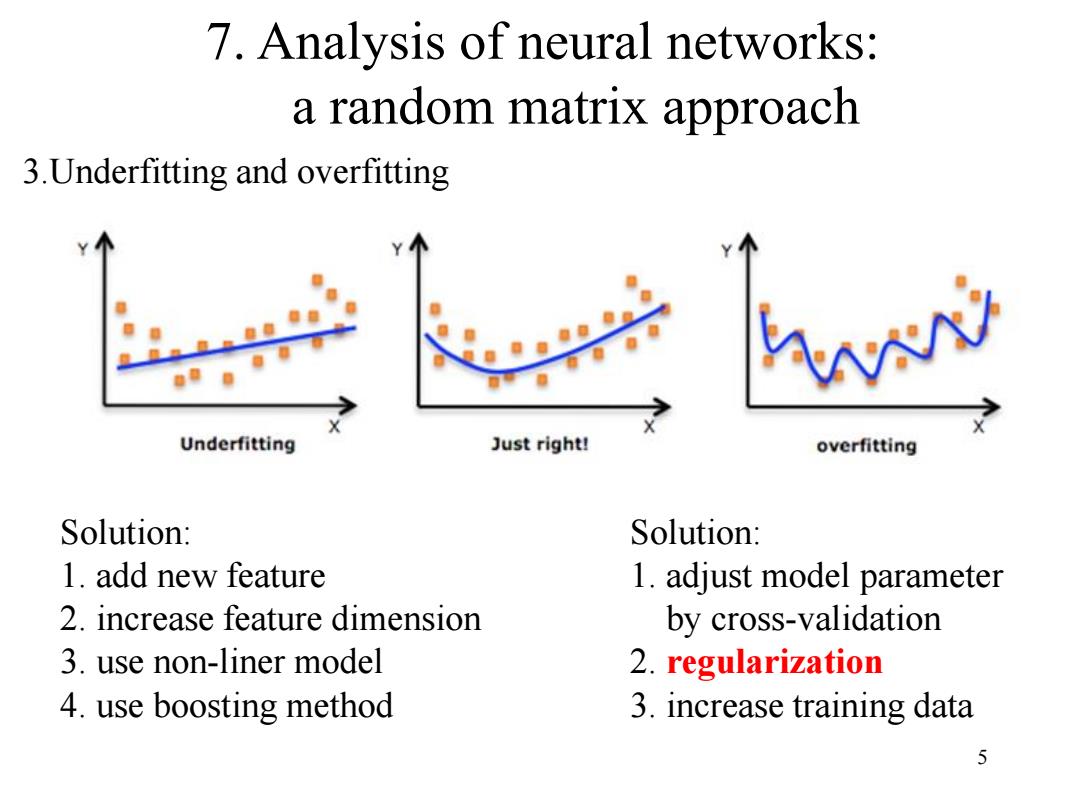
7.Analysis of neural networks: a random matrix approach 3.Underfitting and overfitting Underfitting Just right! overfitting Solution: Solution: 1.add new feature 1.adjust model parameter 2.increase feature dimension by cross-validation 3.use non-liner model 2.regularization 4.use boosting method 3.increase training data 5
5 7. Analysis of neural networks: a random matrix approach 3.Underfitting and overfitting Solution: 1. add new feature 2. increase feature dimension 3. use non-liner model 4. use boosting method Solution: 1. adjust model parameter by cross-validation 2. regularization 3. increase training data
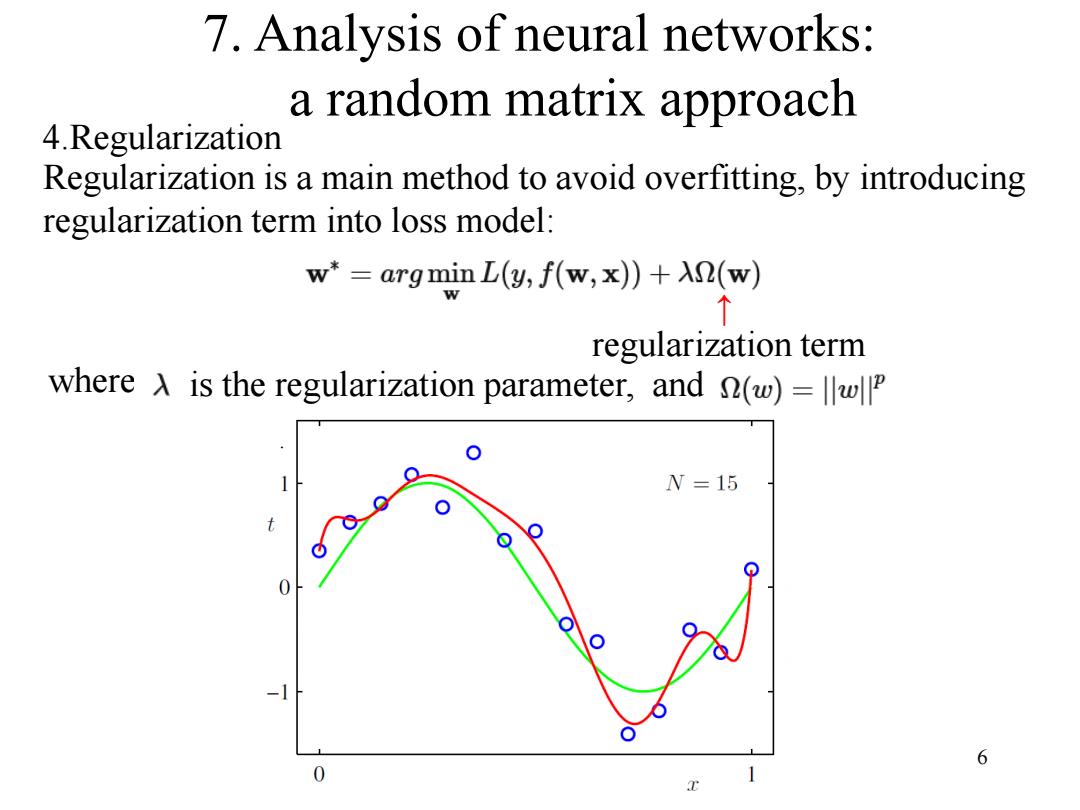
7.Analysis of neural networks: a random matrix approach 4.Regularization Regularization is a main method to avoid overfitting,by introducing regularization term into loss model: w*=argmin L(y,f(w,x))+XR(w) 个 regularization term where A is the regularization parameter,and (w)=w N=15 6 0
6 7. Analysis of neural networks: a random matrix approach 4.Regularization Regularization is a main method to avoid overfitting, by introducing regularization term into loss model: ↑ regularization term where is the regularization parameter, and
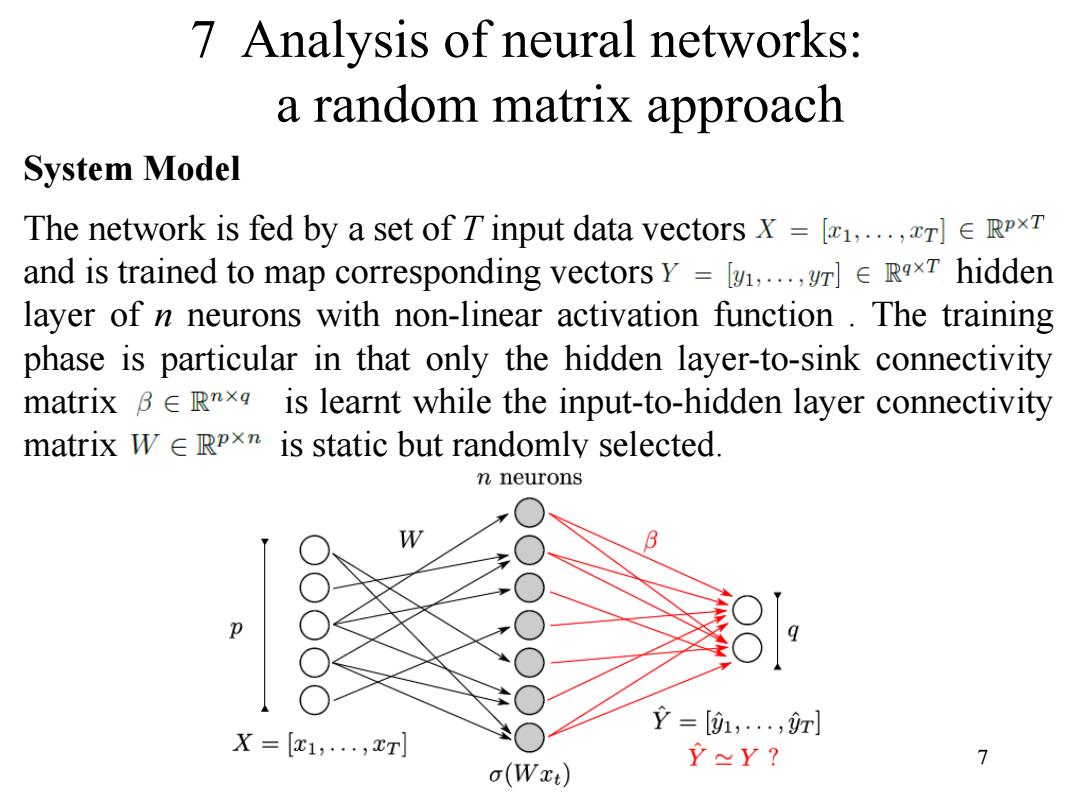
7 Analysis of neural networks: a random matrix approach System Model The network is fed by a set of T input data vectors x [...rE RPxT and is trained to map corresponding vectors Y =,...RxT hidden layer of n neurons with non-linear activation function.The training phase is particular in that only the hidden layer-to-sink connectivity matrix Be RTx is learnt while the input-to-hidden layer connectivity matrix W E RpxT is static but randomly selected n neurons Y=[1,,r] X=[x1,,xT] 7 o(Wxt) Y≈Y?
7 7 Analysis of neural networks: a random matrix approach System Model The network is fed by a set of T input data vectors and is trained to map corresponding vectors hidden layer of n neurons with non-linear activation function . The training phase is particular in that only the hidden layer-to-sink connectivity matrix is learnt while the input-to-hidden layer connectivity matrix is static but randomly selected

7 Analysis of neural networks: a random matrix approach For a given B,the output is thus simply given by y =BT>E RaxT where >=a(wx)and the application of os activation function. During the training phase,the output weight matrix is merely learnt by solving the quadratic minimization problem B=argmingeRnxa 行y-g+呢} where y>o is some constant The solution is explicit and given by g=(宁四+)'r 8
8 For a given , the output is thus simply given by , where , and , and the application of is activation function. During the training phase, the output weight matrix is merely learnt by solving the quadratic minimization problem where is some constant The solution is explicit and given by 7 Analysis of neural networks: a random matrix approach

7 Analysis of neural networks: a random matrix approach The training mean-square error can be written as Fuo()( where we defined Q()=(号T+ylr)- which is the so-called resolvent of the matrix> 9
9 7 Analysis of neural networks: a random matrix approach The training mean-square error can be written as where we defined which is the so-called resolvent of the matrix

7 Analysis of neural networks: a random matrix approach We define A=YTY,recall that our objective is to retrieve a matrix Q() such that.Ttr A(Q()-Q())0.Let us write Q()=(F+yIr)-for some deterministic FeRTxT to be identified.Then,we have tA(Q()-Q()》 -7A0)(F-7)o) -7rAQ)ro)-7∑7.Q)A912 where the first equality uses A-1-B-1=A-(B-A)B-1.while the second equality uses T∑=∑=1以卫, with >i..being the row of 10
10 7 Analysis of neural networks: a random matrix approach We define recall that our objective is to retrieve a matrix such that, . Let us write some deterministic for to be identified. Then, we have where the first equality uses equality uses while the second with being the row of

7 Analysis of neural networks: a random matrix approach Due to (A+VvT)-1v=A-1v/(1+vTA-1v),we now write 7rAQ)-Q》 方扣0P除定益提 1+÷2,.Q-(y)∑, with Q-i=(∑T∑-÷∑,∑,.+ylr)-1 11
11 7 Analysis of neural networks: a random matrix approach Due to , we now write with