
CHAPTER SUNCERTAINTY AND CONSUMER BEHAVIOR 一、QUESTIONS FOR REVIEW 1.What does it mean to say that a person is risk averse?Why are some people likely to be risk averse,while others are risk lovers? a risk-averse person has a diminishing marginal utility of income and prefers a certain income toa gamble with the same e A risk bver has income. The economic explanation of whether an individual is risk averse orrisk loving depends on the shape of the individual's utility function for wealth.Also,a person's risk aversion(or risk loving)depends on the nature of the risk involved and on the person's income. 2.Why is the variance a better measure of variability than the range? Range is the difere between the highest and thewe .Range does not indi cate the probabilities of observing these high or low outcomes. Variance weighs the difference of each outcome from the mean outcome by its probability and.thus,is a more useful measure of variability than the range 3.George has $5,000 to invest in a mutual fund.The expected return on mutual fund A is 15%and the expected return on mutual fund B is 10%.Should George pick mutual fund A or fund B? George's depend the fund,but also on the variability in the expected return on each fund,and on George' preferences.For example,if fund A has a higher standard deviation than fund B and George is risk averse.then he may prefer fund B even though it has a lower icularly risk averse he may chose fund A subject to more variability retur 4.What does it mean for consumers to maximize expected utility? Can you think of a case where a person might not maximize expected utility? The expected utility is the sum of the utilities associated with all possible outcomes,weighted by the probability that each outcome will occur.To maximize expected utility means that the individual chooses the option that yields the highest average utility.where average utility is a probability-weighted sum of all utilities. This theory require sthat the conumer knows the pro obability ofevero me, At times,onsumers either do not know the relevant probabilities or have difficulty in evaluating low-probability,high-payoff events.In some cases,consumers cannot assign a utility level to these high-payoff events,such as when the payoff is the loss of the consumer's life
CHAPTER 5UNCERTAINTY AND CONSUMER BEHAVIOR 一、QUESTIONS FOR REVIEW 1. What does it mean to say that a person is risk averse? Why are some people likely to be risk averse, while others are risk lovers? A risk-averse person has a diminishing marginal utility of income and prefers a certain income to a gamble with the same expected income. A risk lover has an increasing marginal utility of income and prefers an uncertain income to a certain income. The economic explanation of whether an individual is risk averse or risk loving depends on the shape of the individual’s utility function for wealth. Also, a person’s risk aversion (or risk loving) depends on the nature of the risk involved and on the person’s income. 2. Why is the variance a better measure of variability than the range? Range is the difference between the highest possible outcome and the lowest possible outcome. Range does not indicate the probabilities of observing these high or low outcomes. Variance weighs the difference of each outcome from the mean outcome by its probability and, thus, is a more useful measure of variability than the range. 3. George has $5,000 to invest in a mutual fund. The expected return on mutual fund A is 15% and the expected return on mutual fund B is 10%. Should George pick mutual fund A or fund B? George’s decision will depend not only on the expected return for each fund, but also on the variability in the expected return on each fund, and on George’s preferences. For example, if fund A has a higher standard deviation than fund B, and George is risk averse, then he may prefer fund B even though it has a lower expected return. If George is not particularly risk averse he may choose fund A even if it subject to more variability in its expected return. 4. What does it mean for consumers to maximize expected utility? Can you think of a case where a person might not maximize expected utility? The expected utility is the sum of the utilities associated with all possible outcomes, weighted by the probability that each outcome will occur. To maximize expected utility means that the individual chooses the option that yields the highest average utility, where average utility is a probability-weighted sum of all utilities. This theory requires that the consumer knows the probability of every outcome. At times, consumers either do not know the relevant probabilities or have difficulty in evaluating low-probability, high-payoff events. In some cases, consumers cannot assign a utility level to these high-payoff events, such as when the payoff is the loss of the consumer’s life

5.Why do people often want to insure fully against uncertain situations even when the premium paid exceeds the expected value of the loss being insured against. If the cost of insurance is equal to the expected loss (ie.if the insurance is actuarially fair).risk-averse individuals will fully insure against monetary bss. The insurance premium assures the individual of having the same income regardless ofwhether or not a bss occurs Because the insurance is actuarially fair. option of not purchasing insurance.This guarantee of the same income,whateve the outcome,generates more utility for a risk-averse person than the average utility of a high income when there was no loss and the utility of a low income with a loss (ie.because ofrisk aversion.ElU(x)I s U(EIxD). 6.Why is an insu rance con pany likely to behave as ifit is risk neutral even if its nagers are risk-averse individuals? Most large companies have oppe tu nities for diversifying risk.Manage acting for the owners of a company choose a portfolio of independent,profitabl projects at different levels of risk.Of course,shareholders may diversify their risk by investing in several projects in the same way that the insurance company itself diversifies risk by insuring many people.By operating on a sufficiently large scale. insurance companies can assure themselves that over many outcomes the total premiums paid to the company will be equal to the e total amount of me ney paid ou to compensate the losses of the insured.Thus,the insurance company behaves as if it is risk neutral,while the managers,as individuals,might be risk averse. 7.When is it worth paying to obtain more information to reduce uncertainty? Individuals are willing to pay more for information when the utility of the choice with more information.including the cost of gathering the information,is greater than the expected utility ofthe choice without the information 8.How does the diversification of an investor's portfolio avoid risk? An investor reduces risk by investing in many inversely related assets.For example a mutual fund is a portlio of stocks of independent ompanies.If th variance of the return on one company's stock is inversely related to the variance of the return on another company's stock.a portfolio of both stocks will have a lower variance than either stock held separately.As the number of stocks increases the variance in the rate of return on the portfolio as a whole decreases While there is less risk in a portfolio of stocks,risk is not eliminated altogether there market risk in holding such a portfolio,compared to a low-risk asset,such as a U.S government savings bond. 9.Why do some investors put a large portion of their portfolios into risky assets, while others invest largely in risk-free alternatives?(Hint:Do the two investors receive exactly the same return on average?why?)
5. Why do people often want to insure fully against uncertain situations even when the premium paid exceeds the expected value of the loss being insured against? If the cost of insurance is equal to the expected loss, (i.e., if the insurance is actuarially fair), risk-averse individuals will fully insure against monetary loss. The insurance premium assures the individual of having the same income regardless of whether or not a loss occurs. Because the insurance is actuarially fair, this certain income is equal to the expected income if the individual takes the risky option of not purchasing insurance. This guarantee of the same income, whatever the outcome, generates more utility for a risk-averse person than the average utility of a high income when there was no loss and the utility of a low income with a loss (i.e., because of risk aversion, E[U(x)] U(E[x]). 6. Why is an insurance company likely to behave as if it is risk neutral even if its managers are risk-averse individuals? Most large companies have opportunities for diversifying risk. Managers acting for the owners of a company choose a portfolio of independent, profitable projects at different levels of risk. Of course, shareholders may diversify their risk by investing in several projects in the same way that the insurance company itself diversifies risk by insuring many people. By operating on a sufficiently large scale, insurance companies can assure themselves that over many outcomes the total premiums paid to the company will be equal to the total amount of money paid out to compensate the losses of the insured. Thus, the insurance company behaves as if it is risk neutral, while the managers, as individuals, might be risk averse. 7. When is it worth paying to obtain more information to reduce uncertainty? Individuals are willing to pay more for information when the utility of the choice with more information, including the cost of gathering the information, is greater than the expected utility of the choice without the information. 8. How does the diversification of an investor’s portfolio avoid risk? An investor reduces risk by investing in many inversely related assets. For example, a mutual fund is a portfolio of stocks of independent companies. If the variance of the return on one company’s stock is inversely related to the variance of the return on another company’s stock, a portfolio of both stocks will have a lower variance than either stock held separately. As the number of stocks increases, the variance in the rate of return on the portfolio as a whole decreases. While there is less risk in a portfolio of stocks, risk is not eliminated altogether; there is still some market risk in holding such a portfolio, compared to a low-risk asset, such as a U.S. government savings bond. 9. Why do some investors put a large portion of their portfolios into risky assets, while others invest largely in risk-free alternatives? (Hint: Do the two investors receive exactly the same return on average? Why?)

In a market for risky assets.where investors are risk averse,investors demand a on investments that have a higher evel of risk(a higher variance in returns). Although some individuals are willing to accept a higher level of risk in exchange for a higher rate of return,this does not mean that these individuals are less risk averse.On the contrary.they will not invest in risky assets unkess they are compensated for the increased risk. 10.What is an endowment effect?Give an example of such an effect. An endowment effect exists if an individual places a greater value on an item to the value she pac onthe same item when it is not in her or example,many people would refuse topay$5 simple coffee mug but would also refuse to sell a simple coffee mug they won in a contest for the same price even though they got it for free. 11.Jennifer is shopping and sees an attractive shirt.However,the price of $50 is more than she is willing to pay.A few weeks later she finds the same shirt on sale for $25,and buys it.When a friend offers Jennifer $50 for the shirt, she refuses to sell it. Explain Jennifer's behavior To help explain Jennifers behavior,we need to look at the reference point from which she is making the decision.In the first instance.she does not own the shirt so she is not willing to pay the $50 to buy the shirt.In the second instance. she will not accept $50 for the shirt from her friend because her reference point has changed.Once she owns the shirt.she changed the amount by which she valued the shirt.Individuals often value goods more when they own them than when they do not 二、EXERCISES 1.Consider a lottery with three possible outcomes:$125 will be received with probability.2,$100 with probability.3,and $50 with probability.5. a.What is the expected value ofthe lottery? The expected value,EV,of the lottery isequal to the sum of the returns weighted by their probabilities: EV=(0.2)$125)+(0.3)$100)+(0.5)$50)=$80 b.What is the variance of the outcomes ofthe lottery? The variance,is the sum of the squared deviations from the mean.$80. weighted by their probabilities 2=(0.2125.802+(0.3100.80+(0.560.80y=$975. c What would a risk-neutral person pay to play the lottery? Arisk-neutral person would pay the expected value ofthe lottery:$8
In a market for risky assets, where investors are risk averse, investors demand a higher return on investments that have a higher level of risk (a higher variance in returns). Although some individuals are willing to accept a higher level of risk in exchange for a higher rate of return, this does not mean that these individuals are less risk averse. On the contrary, they will not invest in risky assets unless they are compensated for the increased risk. 10. What is an endowment effect? Give an example of such an effect. An endowment effect exists if an individual places a greater value on an item that is in her possession as compared to the value she places on the same item when it is not in her possession. For example, many people would refuse to pay $5 for a simple coffee mug but would also refuse to sell a simple coffee mug they won in a contest for the same price even though they got it for free. 11. Jennifer is shopping and sees an attractive shirt. However, the price of $50 is more than she is willing to pay. A few weeks later she finds the same shirt on sale for $25, and buys it. When a friend offers Jennifer $50 for the shirt, she refuses to sell it. Explain Jennifer’s behavior. To help explain Jennifer’s behavior, we need to look at the reference point from which she is making the decision. In the first instance, she does not own the shirt so she is not willing to pay the $50 to buy the shirt. In the second instance, she will not accept $50 for the shirt from her friend because her reference point has changed. Once she owns the shirt, she changed the amount by which she valued the shirt. Individuals often value goods more when they own them than when they do not. 二、EXERCISES 1. Consider a lottery with three possible outcomes: $125 will be received with probability .2, $100 with probability .3, and $50 with probability .5. a. What is the expected value of the lottery? The expected value, EV, of the lottery is equal to the sum of the returns weighted by their probabilities: EV = (0.2)($125) + (0.3)($100) + (0.5)($50) = $80. b. What is the variance of the outcomes of the lottery? The variance, 2, is the sum of the squared deviations from the mean, $80, weighted by their probabilities: 2 = (0.2)(125 - 80)2 + (0.3)(100 - 80)2 + (0.5)(50 - 80)2 = $975. c. What would a risk-neutral person pay to play the lottery? A risk-neutral person would pay the expected value of the lottery: $80

2.Suppose you have invested in a new computer company whose profitability depends on ()whether the U.S.Congress passes atarif that raises the Japanese computers and (2)whether the U.S.economy grows slowly or quickly What are the four mutually exclusive states of the world that you should be concerned about? The four mutually exclusive states may be represented as: Congress passes tariff Congress does not pass tariff Slow growth rate State 1: State 2: Slow growth with tariff Slow growth without tarif Fast growth rate State 3: State 4: ast growth with tariff Fast growth without tariff 3.Richard is deciding whether to buy astate lottery ticket.Each ticket costs$ and the probability of the following winning payoffs is given as follows: Probability Return 0.50 $0.00 0.25 $1.00 0.20 $2.00 0.05 $7.50 a.What is the expected value of Richard's payoff if he buys a lottery ticket? What is the variance? The expected value of the ttery isequal to the sum of by their probabilities EV=(0.50)+(0.25)s1.00)+(0.2(2.00)+(0.05)$7.50)=$1.025 The variance is the sum of the squared deviation from the mean,$1025 weighted by their probabilities: o2=(0.5)0·1.025)¥+(0.25(1·1.025)¥+(0.2(2·1.025)2+(0.05)(7.5-1.025)2.or o2=$2.812. b.Richard's nickname is "No-risk Rick."He is an extremely risk-averse individual.Would he buy the ticket? An extremely risk-averse individual will probably not buy the ticket,even though the expected outcome is higher than the price,$1025$1.00.The in the xpected Forexampk.ifh wl1oand be u0 ticket.be wuld have 59.0 ompens Rick for the risk $10.00,$11.00,and $16.50,respectively,under the four possible outcomes.Let us assume that his utility function is U=was,where W is his wealth.Then his expected utility is:
2. Suppose you have invested in a new computer company whose profitability depends on (1) whether the U.S. Congress passes a tariff that raises the cost of Japanese computers and (2) whether the U.S. economy grows slowly or quickly. What are the four mutually exclusive states of the world that you should be concerned about? The four mutually exclusive states may be represented as: Congress passes tariff Congress does not pass tariff Slow growth rate State 1: Slow growth with tariff State 2: Slow growth without tariff Fast growth rate State 3: Fast growth with tariff State 4: Fast growth without tariff 3. Richard is deciding whether to buy a state lottery ticket. Each ticket costs $1, and the probability of the following winning payoffs is given as follows: Probability Return 0.50 $0.00 0.25 $1.00 0.20 $2.00 0.05 $7.50 a. What is the expected value of Richard’s payoff if he buys a lottery ticket? What is the variance? The expected value of the lottery is equal to the sum of the returns weighted by their probabilities: EV = (0.5)(0) + (0.25)($1.00) + (0.2)($2.00) + (0.05)($7.50) = $1.025 The variance is the sum of the squared deviation from the mean, $1.025, weighted by their probabilities: 2 = (0.5)(0 - 1.025)2 + (0.25)(1 - 1.025)2 + (0.2)(2 - 1.025)2 + (0.05)(7.5 - 1.025)2, or 2 = $2.812. b. Richard’s nickname is “No-risk Rick.” He is an extremely risk-averse individual. Would he buy the ticket? An extremely risk-averse individual will probably not buy the ticket, even though the expected outcome is higher than the price, $1.025 > $1.00. The difference in the expected return is not enough to compensate Rick for the risk. For example, if his wealth is $10 and he buys a $1.00 ticket, he would have $9.00, $10.00, $11.00, and $16.50, respectively, under the four possible outcomes. Let us assume that his utility function is U = W0.5, where W is his wealth. Then his expected utility is:

EU=(0.59s)+0.25)00+(0.21105)+(0.05)06.5)=3.157. c.Suppose Richard was offered insurance against losing any money.If he buys 1,000 lottery tickets,how much would he be willing to pay to insure his gamble? If Richard buys 1000 tickets.it is likely that he will have $1025 minus the the exp $1,025.is greater than the cost,00. elf by buy ng a larg number of tickets.Given that Richard is risk averse though,he may still want t buy insurance.The amount he would be willing to pay is equal to the risk premium,which is the amount of money that Richard would pay to avoid the risk. See figure 5.4 in the text To calculate the risk pr emium.you need to know the utility function.If the utility function isU=,then his expected utility from the EU=(0.50°5)+(0.25)00005)+(0.2)000°)+(0.0575005)21.18. This is less than the utility he would get from keeping his $1000 which is U=100005=31.62.To find the risk premium,find the level of income that woul d.In the long run,given the price ofthe lottery ticket and the probability/return table,what do you think the state would do about the lottery? In the long run,the state lottery will be bankrupt!Given the price of the ticket and the probabilities.the lottery is a money loser.The state must either raise the price of a ticket or lower the probability of positive payoff e an investor is concerned about a business choice in which there are e prosp ects,whose probability and returns are given below Probability Return 0.4 $100 .3 30 0.3 30 What is the expected value of the uncertain investment?What is the variance? The expected value of the return on this investment is EV=(0.4(100)+(0.330)+(0.3(-30)=$40 The variance is 2=(0.4100.40P+(0.330.40+0.3-30.40P=2,940
EU = (0.5) 9 0.5 ( )+ (0.25) 100.5 ( )+ (0.2) 110.5 ( )+ (0.05) 16.5 0.5 ( )= 3.157. This is less than 3.162, which is the utility associated with not buying the ticket (U(10) = 100.5 = 3.162). He would prefer the sure thing, i.e., $10. c. Suppose Richard was offered insurance against losing any money. If he buys 1,000 lottery tickets, how much would he be willing to pay to insure his gamble? If Richard buys 1,000 tickets, it is likely that he will have $1,025 minus the $1,000 he paid, or $25. He would not buy any insurance, as the expected return, $1,025, is greater than the cost, $1,000. He has insured himself by buying a large number of tickets. Given that Richard is risk averse though, he may still want to buy insurance. The amount he would be willing to pay is equal to the risk premium, which is the amount of money that Richard would pay to avoid the risk. See figure 5.4 in the text. To calculate the risk premium, you need to know the utility function. If the utility function is U = W0.5, then his expected utility from the 1,000 lottery tickets is EU = (0.5) 0 0.5 ( )+ (0.25) 10000.5 ( )+(0.2) 20000.5 ( )+ (0.05) 75000.5 ( )= 21.18. This is less than the utility he would get from keeping his $1000 which is U=10000.5=31.62. To find the risk premium, find the level of income that would guarantee him a utility of 21.18, which is $448.59. This means he would pay $1000-$448.59=$551.41 to insure his gamble. d. In the long run, given the price of the lottery ticket and the probability/return table, what do you think the state would do about the lottery? In the long run, the state lottery will be bankrupt! Given the price of the ticket and the probabilities, the lottery is a money loser. The state must either raise the price of a ticket or lower the probability of positive payoffs. 4. Suppose an investor is concerned about a business choice in which there are three prospects, whose probability and returns are given below: Probability Return 0.4 $100 0.3 30 0.3 -30 What is the expected value of the uncertain investment? What is the variance? The expected value of the return on this investment is EV = (0.4)(100) + (0.3)(30) + (0.3)(-30) = $40. The variance is 2 = (0.4)(100 - 40)2 + (0.3)(30 - 40)2 + (0.3)(-30 - 40)2 = $2,940

5.You are an insurance agent who has to write a policy for a new client named Sam.His company,Society for Creative Alternatives to Mayonnaise (SCAM), working on a low-fat,low-chol sterol mayonnaise substitute for the sandwich condiment industry.The sandwich industry will pay top dollar to whoever invents such a mayonnaise substitute first.Sam's SCAM seems like a very risky proposition to you.You have calculated his possible returns table as follows. Probability Return ,999 -81,000,000 (he fails) .001 $1.000.000.000 (he succeeds and sells the formula a.What is the expected return of his project?What is the variance? The expected return,ER,ofthe investment is ER=(0.999-1,000.000)+0.001)1,000.000,000)=$1.000 The variance is 2=(0.999-1,000,000.1.000y2+0.0011,000,000,000.1.000y,0 c2=1,000,998,999.000,000 b.What is the most Sam is willing to pay for insurance?Assume Sam is risk neutral. Because Sam is risk neutral and because the expected outcome is S1,000.Sam is unwilling to buy insurance. e.Suppose you found out that the Japanese are on the verge of introducing their onnaise substitute next month.Sam does not know this and has j扣stur ed do nal offer ssume that Sam tells you SCAM is only six months away from perfecting its mayonnaise substitute and that you know what you know about the Japanese.Would you raise or lower your policy premium on any subsequent proposal to Sam?Based on his information,would Sam accept? The entry of the Japanese lowers Sam's probability of a high payoff.For example,assume that the probability of the billion dollar payoff is owered to. Then the expected outcome is: (1.0-s1,000,000)+(0.0s1,000,000,000)=-$1,000,000. Therefre,you should raise the policy premium substantially.But Sam,not knowing about the Japanese entry,will continue to refuse your offers to insure his losses」
5. You are an insurance agent who has to write a policy for a new client named Sam. His company, Society for Creative Alternatives to Mayonnaise (SCAM), is working on a low-fat, low-cholesterol mayonnaise substitute for the sandwich condiment industry. The sandwich industry will pay top dollar to whoever invents such a mayonnaise substitute first. Sam’s SCAM seems like a very risky proposition to you. You have calculated his possible returns table as follows. Probability Return .999 -$1,000,000 (he fails) .001 $1,000,000,000 (he succeeds and sells the formula) a. What is the expected return of his project? What is the variance? The expected return, ER, of the investment is ER = (0.999)(-1,000,000) + (0.001)(1,000,000,000) = $1,000. The variance is 2 = (0.999)(-1,000,000 - 1,000)2 + (0.001)(1,000,000,000 - 1,000)2 , or 2 = 1,000,998,999,000,000. b. What is the most Sam is willing to pay for insurance? Assume Sam is risk neutral. Because Sam is risk neutral and because the expected outcome is $1,000, Sam is unwilling to buy insurance. c. Suppose you found out that the Japanese are on the verge of introducing their own mayonnaise substitute next month. Sam does not know this and has just turned down your final offer of $1,000 for the insurance. Assume that Sam tells you SCAM is only six months away from perfecting its mayonnaise substitute and that you know what you know about the Japanese. Would you raise or lower your policy premium on any subsequent proposal to Sam? Based on his information, would Sam accept? The entry of the Japanese lowers Sam’s probability of a high payoff. For example, assume that the probability of the billion dollar payoff is lowered to zero. Then the expected outcome is: (1.0)(-$1,000,000) + (0.0)(($1,000,000,000) = -$1,000,000. Therefore, you should raise the policy premium substantially. But Sam, not knowing about the Japanese entry, will continue to refuse your offers to insure his losses

6.Suppose that Natasha's utility function is given by)=107,where I represents annual income in thousands of dollars. a.Is Natasha risk loving,risk neutral,or risk averse?Explain. Natasha is risk averse.To show this,assume that she has $10.000 and is offered a gamble of a $1,000 gain with 50 percent pmobability and a S1,000 loss with 50 percent probability.Her utility of $10.000 is 10.(u(=10*1010).Her expected utility is: EU=0.59006)+0.51100.6)=9.987<10 She would avoid the gamble.If she were risk neutral,she would be indifferent between the $10.000 and the gamble:whereas if she were risk loving.she would You can also see that she is risk averse by noting that the second derivative is negative,implying diminishing marginal utility. b.Suppose that Natasha is currently earning an income of $40,000(I=40)and can earn that income next year with certainty.She is offered a chance to take a new job that offers a .6 probability of earning $44.000,and a.4 probability of earning $33.000.Should she take the new job? The utility of her current salary iswhich is 20.The expected utility of the new job is EU=0.6440.5)+0.4330.)=19.85 which is less than 20.Therefore,she should not take the job. c.In (b),would Natasha be willing to buy insurance to protect against the variable income associated with the new job?If so,how much would she be willing to pay for that insurance?(Hint:What is the risk premium?) Assuming that she takes the new job,Natasha would be willing to pay a risk sa kvel of utility equalo bleequal to 19.85.Substituting into her utility function we have. (101p.s,and solving for I we find the income associated with the gamble to be $39.410.Thus.Natasha would be willing to pay for insurance equal to the risk premium.S40.000-S39,410=$590 7.Suppose that two investments have the same three pavoffs.but the sociated with each payoff differs,as illustrated in the table Probabilities for Investment A Probabilities for Investment 旦 $300 0.10 0.30 $250 0.80 0.40
6. Suppose that Natasha’s utility function is given by u(I) = 10I , where I represents annual income in thousands of dollars. a. Is Natasha risk loving, risk neutral, or risk averse? Explain. Natasha is risk averse. To show this, assume that she has $10,000 and is offered a gamble of a $1,000 gain with 50 percent probability and a $1,000 loss with 50 percent probability. Her utility of $10,000 is 10, (u(I) = 10 *10 = 10). Her expected utility is: EU = (0.5)(900.5 ) + (0.5)(1100.5 ) = 9.987 < 10. She would avoid the gamble. If she were risk neutral, she would be indifferent between the $10,000 and the gamble; whereas, if she were risk loving, she would prefer the gamble. You can also see that she is risk averse by noting that the second derivative is negative, implying diminishing marginal utility. b. Suppose that Natasha is currently earning an income of $40,000 (I = 40) and can earn that income next year with certainty. She is offered a chance to take a new job that offers a .6 probability of earning $44,000, and a .4 probability of earning $33,000. Should she take the new job? The utility of her current salary is 4000.5, which is 20. The expected utility of the new job is EU = (0.6)(4400.5 ) + (0.4)(3300.5 ) = 19.85, which is less than 20. Therefore, she should not take the job. c. In (b), would Natasha be willing to buy insurance to protect against the variable income associated with the new job? If so, how much would she be willing to pay for that insurance? (Hint: What is the risk premium?) Assuming that she takes the new job, Natasha would be willing to pay a risk premium equal to the difference between $40,000 and the utility of the gamble so as to ensure that she obtains a level of utility equal to 20. We know the utility of the gamble is equal to 19.85. Substituting into her utility function we have, 19.85 = (10I) 0.5, and solving for I we find the income associated with the gamble to be $39,410. Thus, Natasha would be willing to pay for insurance equal to the risk premium, $40,000 - $39,410 = $590. 7. Suppose that two investments have the same three payoffs, but the probability associated with each payoff differs, as illustrated in the table below: Payoff Probabilities for Investment A Probabilities for Investment B $300 0.10 0.30 $250 0.80 0.40

8200 0.10 0.30 a.Find the expected return and standard deviation ofeach investment The expected value ofthe return on investment Ais EV=0.1300)+(0.8250)+(0.1200)=s250 The variance on investment A is 2=(0.1300-250+(0.8250-2502+(0.1200-250P=$500 The expected value ofthe return on investment Bis EV=(0.3)300)+(0.4250)+(0.3200)=s250 The variance on investment B is 2=(0.3)300250p2+(0.4250-250y+0.3)200250p=$1,500 b.Jill has the utility function U=5/,where I denotes the payoff Which investment will she choose? Jill's expected utility from investment A is EU=.1*6*300)+.8*6*250)+.1*6*200=1,250. Jill's expected utility from investment B is EU=,3*(6*300+.4*(6*250+.3*(6*200)=1,250. Since both investments give Jill the same expected utility she will be indifferent between the two. c.Ken has the utility function U=5/.Which investment will he choose? Ken's expected utility from investment A is EU=.1*(5*300)0.5+.8*(5*250)0.5+.1*(5*200)0.5=35.32 Ken's expected utility from investment B is EU=.3*(5*3000.5+.4*(6*2500.+.3*(6*2000.5=35.25. ken will choose investment a since it has a higher expected utility Notice that since Ken is risk averse,he will prefer the investment with less variability. d.Laura has the utility function U=5/.Which investment will she choose? Laura's expected utility from investment Ais EU=.1*(6*300*300+.8*6*250*250)+.1*6*200*200=315,000 Laura's expected utility from investment B is EU=.3*(6*300*300+.4*(6*250*250)+.3*(6*200*200=320,000 Laura will choose investment B since it has a higher expected utility
$200 0.10 0.30 a. Find the expected return and standard deviation of each investment. The expected value of the return on investment A is EV = (0.1)(300) + (0.8)(250) + (0.1)(200) = $250. The variance on investment A is 2 = (0.1)(300 - 250)2 + (0.8)(250 - 250)2 + (0.1)(200 - 250)2 = $500. The expected value of the return on investment B is EV = (0.3)(300) + (0.4)(250) + (0.3)(200) = $250. The variance on investment B is 2 = (0.3)(300 - 250)2 + (0.4)(250 - 250)2 + (0.3)(200 - 250)2 = $1,500. b. Jill has the utility function U = 5I , where I denotes the payoff. Which investment will she choose? Jill’s expected utility from investment A is EU=.1*(5*300)+.8*(5*250)+.1*(5*200)=1,250. Jill’s expected utility from investment B is EU=.3*(5*300)+.4*(5*250)+.3*(5*200)=1,250. Since both investments give Jill the same expected utility she will be indifferent between the two. c. Ken has the utility function U = 5I . Which investment will he choose? Ken’s expected utility from investment A is EU=.1*(5*300)0.5+.8*(5*250)0.5+.1*(5*200)0.5=35.32. Ken’s expected utility from investment B is EU=.3*(5*300)0.5+.4*(5*250)0.5+.3*(5*200)0.5=35.25. Ken will choose investment A since it has a higher expected utility. Notice that since Ken is risk averse, he will prefer the investment with less variability. d. Laura has the utility function U = 5I 2 . Which investment will she choose? Laura’s expected utility from investment A is EU=.1*(5*300*300)+.8*(5*250*250)+.1*(5*200*200)=315,000. Laura’s expected utility from investment B is EU=.3*(5*300*300)+.4*(5*250*250)+.3*(5*200*200)=320,000. Laura will choose investment B since it has a higher expected utility

8.As the owner of a family farm whose wealth is $250,000,you must choose between sitting thiss son safe money market fund ($200,000)in ating summer corn. Planting costs S200,000,with a six-month time to harvest.If there is rain,planting summer corn will yield $500,000 in revenues at harvest.If there is a drought,planting will yield $50,000 in revenues at harvest.As a third choice,you can purchase AgriCorp drought-resistant summer corn at a cost of $250,000 that will yield s500,000im revenues at harvest if there is rain ,and$350, 000 in reven harvest if there is a drought.You are risk averse and your preferences for family wealth (W)are specified by the relationship U(W)=W.The probability of a summer drought is 0.30 and the probability of summer rain is0.70.Which of the three options should you cho te? Explain. ected utility of wealth under the three option ceadhhieatnentals250bw0pl咖grhatereriermedomgoiag investing in the safe financial asset.Expected utility under the safe option allowing for the fact that your initial wealth is S250,000 is: EU)=(250,000+200,000(1+.05-5=678.23. Expected utility with regular corn,again including your initial wealth: EU=.7(250,000+500.000-200.000》5+.3250,000+60,.000- 200,0005=519.13+94.87=614 Expected utility with drought-resistant corn,again including your initial wealth: EU)=.7250,000+(600,000 .250,000)5+.3250,000+(350,000 250,00005=494.975+177.482=672.46. You should choose the option with the highest expected utility,which is the safe option of not planting corn. 9.Draw a utility function over income u(D)that has the property that a man is a risk lover when his income is low but a risk averter when his income is high. Can you explain why such a utility function might reasonably deseribe a person's Preferences? Consider an individual who needs a cer ain level of incom e,in order to stay alive.An increase in income abovewill have a diminishing marginal utility. Below I,the individual will be a risk bver and will take unfair gambles in an effort to make large gains in income.Above the individual will purchase insurance against losses
8. As the owner of a family farm whose wealth is $250,000, you must choose between sitting this season out and investing last year’s earnings ($200,000) in a safe money market fund paying 5.0% or planting summer corn. Planting costs $200,000, with a six-month time to harvest. If there is rain, planting summer corn will yield $500,000 in revenues at harvest. If there is a drought, planting will yield $50,000 in revenues at harvest. As a third choice, you can purchase AgriCorp drought-resistant summer corn at a cost of $250,000 that will yield $500,000 in revenues at harvest if there is rain, and $350,000 in revenues at harvest if there is a drought. You are risk averse and your preferences for family wealth (W) are specified by the relationship U(W ) = W . The probability of a summer drought is 0.30 and the probability of summer rain is 0.70. Which of the three options should you choose? Explain. You need to calculate expected utility of wealth under the three options. Wealth is equal to the initial $250,000 plus whatever is earned on growing corn, or investing in the safe financial asset. Expected utility under the safe option allowing for the fact that your initial wealth is $250,000 is: E(U) = (250,000 + 200,000(1 + .05)).5 = 678.23. Expected utility with regular corn, again including your initial wealth: E(U) = .7(250,000 + (500,000 -200,000)).5 + .3(250,000 + (50,000 - 200,000)).5 = 519.13 + 94.87 = 614. Expected utility with drought-resistant corn, again including your initial wealth: E(U) = .7(250,000 + (500,000 - 250,000)).5 + .3(250,000 + (350,000 - 250,000)).5 = 494.975 + 177.482 = 672.46. You should choose the option with the highest expected utility, which is the safe option of not planting corn. 9. Draw a utility function over income u(I) that has the property that a man is a risk lover when his income is low but a risk averter when his income is high. Can you explain why such a utility function might reasonably describe a person’s preferences? Consider an individual who needs a certain level of income, I*, in order to stay alive. An increase in income above I* will have a diminishing marginal utility. Below I*, the individual will be a risk lover and will take unfair gambles in an effort to make large gains in income. Above I*, the individual will purchase insurance against losses
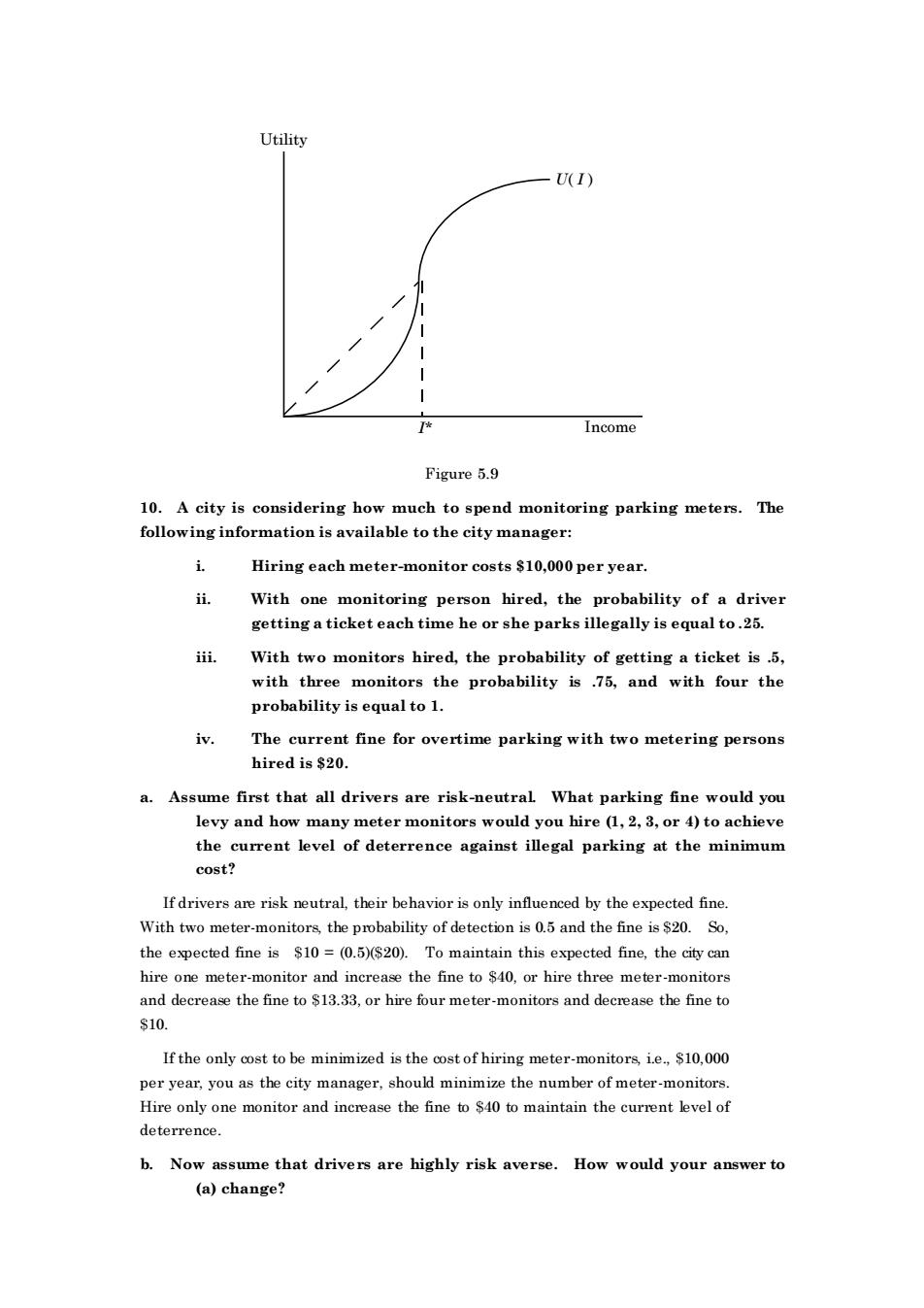
Utility -U(I) Income Figure 5.9 10.A city is considering how much to spend monitoring parking meters.The following information is available to the city manager: Hiring each meter-monitor costs $10,000 per year i进. With one monitoring person hired,the probability of a driver zetting a ticket each time he or she parks illegally is equal to.25. iii. With two monitors hired.the probability of getting a ticket is.5. with three monitors the probability is75, and with four the probability is equal to 1 iv. The current fine for overtime parking with two metering persons hired is $20. a.Assume first that all drivers are risk-neutral What parking fine would you levy and how many meter monitors would you hire (1,2,3,or 4)to achieve the current level of deterrence against illegal parking at the minimum cost? If driversare,their behavior is only by the exp ected fine the expected fine is $10=(0.5)($20).To maintain this expected fine,the city can hire one meter-monitor and increase the fine to $40,or hire three meter-monitors and decrease the fine to $13.33,or hire four meter-monitors and decrease the fine to S10 If th minimized is the ofhir monitorsie$10.000 per year,you as the city manager,shoul e the number of meter-monitors Hire only one monitor and increase the fine to $40 to maintain the current level o deterrence. b.Now assume that drivers are highly risk averse.How would your answer to (a)change?
Utility Income U( I ) I* Figure 5.9 10. A city is considering how much to spend monitoring parking meters. The following information is available to the city manager: i. Hiring each meter-monitor costs $10,000 per year. ii. With one monitoring person hired, the probability of a driver getting a ticket each time he or she parks illegally is equal to .25. iii. With two monitors hired, the probability of getting a ticket is .5, with three monitors the probability is .75, and with four the probability is equal to 1. iv. The current fine for overtime parking with two metering persons hired is $20. a. Assume first that all drivers are risk-neutral. What parking fine would you levy and how many meter monitors would you hire (1, 2, 3, or 4) to achieve the current level of deterrence against illegal parking at the minimum cost? If drivers are risk neutral, their behavior is only influenced by the expected fine. With two meter-monitors, the probability of detection is 0.5 and the fine is $20. So, the expected fine is $10 = (0.5)($20). To maintain this expected fine, the city can hire one meter-monitor and increase the fine to $40, or hire three meter-monitors and decrease the fine to $13.33, or hire four meter-monitors and decrease the fine to $10. If the only cost to be minimized is the cost of hiring meter-monitors, i.e., $10,000 per year, you as the city manager, should minimize the number of meter-monitors. Hire only one monitor and increase the fine to $40 to maintain the current level of deterrence. b. Now assume that drivers are highly risk averse. How would your answer to (a) change?