
CHAPTER 6PRODUCTION QUESTIONS FOR REVIEW 1.What is a production function?How does a long-run production function differ from a short-run production function? A production function represents how inputs are transformed into outputs by firm.We focu on the firm with one output and aggregate all inputs or factorso production into one of several categories such as labor,capital,and materials.In the short run,one or more factors of production cannot be changed.As time goes by, the firm has the opportunity to change the levels of all inputs.In the long-run production variable. 2.Why is the marginal produet of labor likely to inerease initially in the short run as more of the variable input is hired? The marginal product of labor is likely to increase initially because when there are more workers,each is able to specialize on an aspect of the production process in which he or she is particularly skilled.For example,think of the typical fast food restaurant. If there is only one worker,he will need to prepare the burgers,fries,and sodas,as well can be served in an hour.With twoor able to specialize and the marginal product(number of customers served per hour)is likely to increase as we move from one to two to three workers. Eventually,there will be enough workers and there will be no more gains from specialization.At this point,the marginal product will diminish. 3.Why does production eventually experience diminishing marginal returns to labor in the short run? The marginal product of labor will eventually diminish because there will be at least one fixed f actor of production,suc as capital With capital the workpl ce will eventually become so congested,that the productivity of additional workers will decline.Also,with capital fixed,as more workers are added,they will need to share the fixed capital,which will eventually cause the marginal product of labor to diminish htoo miny workers Think forexample of anoffce where m0 e employees computers,the marginal product of each additional employee will diminish. 4.You are an employer seeking to fill a vacant position on an assembly line Are you more concerned with the average product of labor or the marginal produet of labor for the last person hired?If you observe that your average product is just beginning to decline,should you hire any more workers?What does this situation imply about the marginal product of your last worker hired? In filling a vacant with the marginal product of the last worker hired because the marginal product measures the effecton output. or total product,of hiring another worker.This in turn will help to determine the
CHAPTER 6PRODUCTION 一、QUESTIONS FOR REVIEW 1. What is a production function? How does a long-run production function differ from a short-run production function? A production function represents how inputs are transformed into outputs by a firm. We focus on the firm with one output and aggregate all inputs or factors of production into one of several categories, such as labor, capital, and materials. In the short run, one or more factors of production cannot be changed. As time goes by, the firm has the opportunity to change the levels of all inputs. In the long-run production function, all inputs are variable. 2. Why is the marginal product of labor likely to increase initially in the short run as more of the variable input is hired? The marginal product of labor is likely to increase initially because when there are more workers, each is able to specialize on an aspect of the production process in which he or she is particularly skilled. For example, think of the typical fast food restaurant. If there is only one worker, he will need to prepare the burgers, fries, and sodas, as well as take the orders. Only so many customers can be served in an hour. With two or three workers, each is able to specialize and the marginal product (number of customers served per hour) is likely to increase as we move from one to two to three workers. Eventually, there will be enough workers and there will be no more gains from specialization. At this point, the marginal product will diminish. 3. Why does production eventually experience diminishing marginal returns to labor in the short run? The marginal product of labor will eventually diminish because there will be at least one fixed factor of production, such as capital. With capital fixed, the workplace will eventually become so congested, that the productivity of additional workers will decline. Also, with capital fixed, as more workers are added, they will need to share the fixed capital, which will eventually cause the marginal product of labor to diminish as the capital is spread across too many workers. Think for example of an office where there are only three computers. As more and more employees must share the computers, the marginal product of each additional employee will diminish. 4. You are an employer seeking to fill a vacant position on an assembly line. Are you more concerned with the average product of labor or the marginal product of labor for the last person hired? If you observe that your average product is just beginning to decline, should you hire any more workers? What does this situation imply about the marginal product of your last worker hired? In filling a vacant position, you should be concerned with the marginal product of the last worker hired because the marginal product measures the effect on output, or total product, of hiring another worker. This in turn will help to determine the

revenue generated by hiring another worker,which can then be compared to the cost of hiring another worker The point at which the average product begins to decline is the point whe average product isequal tomarginal product.When average product declines the marginal product of the last worker hired is lower than the average product of previously hired workers. Although adding more workers results in a further decline in average product, total product continues to increase.so it may still be advantageous to hire another worker. 5.What is the difference between a production function and an isoquant? A production function describes the maximum output that can be achieved with any given combination of inputs.An isoquant identifiesall of the different combinations of the inputs that can be used to produce one particular level of output. 6.Faced with constantly changing conditions,why would a firm ever keep any factors fixed?What criteria determine whether a factor is fixed or variable? Whether a factor is fixed or variable depends on the time horizon in consideration:all factors are fixed in the very short run:all factors are variable in the long run.As stated in the text:"All fixed inputs in the short run out omes previous long-run ons based on firms mates of wha the: could profitably produce and sell"Some factors are fixed in the short run,whether the firm likes it or not,simply because it takes time to adjust the level of the variables.For example.the firm may be legally bound by a lease on a building ome employees may that must be upheld,or construction of a nev take mbe of Recall that th。 as a specific number of months or years,but as that period of time where som inputs cannot be changed for reasons such as those given above. 7.Isoquants can be convex,linear,or Lshaped.What does each of these shapes tell you about the nature of the production function?What does each of these shapes tell you about the MRTS? Convex isoquants imply that within some range,some number of units of one input can be substituted foraunit of theother input,and output can be maintained at the same level.In this case,the MRTS is diminishing as we move down along the isoquant. Linear isoquants imply that the slope,or the MRTS,is constant.This means that the same number of units of one input can always be exchanged for a unit of the other input and output can be maintained.The inputs are perfect substitutes.L-shaped isoquants imply that the inputs are perfect omple tsor that the firm is producing undera fixed proportions type of technology.In this case the firm cannot give up one input in exchange for the other and still maintain the same level of output.For example,the firm may require exactly 4 units of capital for each unit of labor,in which case one input cannot be substituted for the other. 8.Can an isoquant ever slope upwards?Explain
revenue generated by hiring another worker, which can then be compared to the cost of hiring another worker. The point at which the average product begins to decline is the point where average product is equal to marginal product. When average product declines, the marginal product of the last worker hired is lower than the average product of previously hired workers. Although adding more workers results in a further decline in average product, total product continues to increase, so it may still be advantageous to hire another worker. 5. What is the difference between a production function and an isoquant? A production function describes the maximum output that can be achieved with any given combination of inputs. An isoquant identifies all of the different combinations of the inputs that can be used to produce one particular level of output. 6. Faced with constantly changing conditions, why would a firm ever keep any factors fixed? What criteria determine whether a factor is fixed or variable? Whether a factor is fixed or variable depends on the time horizon in consideration: all factors are fixed in the very short run; all factors are variable in the long run. As stated in the text: “All fixed inputs in the short run represent outcomes of previous long-run decisions based on firms’ estimates of what they could profitably produce and sell.” Some factors are fixed in the short run, whether the firm likes it or not, simply because it takes time to adjust the level of the variables. For example, the firm may be legally bound by a lease on a building, some employees may have contracts that must be upheld, or construction of a new facility may take some number of months. Recall that the short run is not defined as a specific number of months or years, but as that period of time where some inputs cannot be changed for reasons such as those given above. 7. Isoquants can be convex, linear, or L-shaped. What does each of these shapes tell you about the nature of the production function? What does each of these shapes tell you about the MRTS? Convex isoquants imply that within some range, some number of units of one input can be substituted for a unit of the other input, and output can be maintained at the same level. In this case, the MRTS is diminishing as we move down along the isoquant. Linear isoquants imply that the slope, or the MRTS, is constant. This means that the same number of units of one input can always be exchanged for a unit of the other input and output can be maintained. The inputs are perfect substitutes. L-shaped isoquants imply that the inputs are perfect complements, or that the firm is producing under a fixed proportions type of technology. In this case the firm cannot give up one input in exchange for the other and still maintain the same level of output. For example, the firm may require exactly 4 units of capital for each unit of labor, in which case one input cannot be substituted for the other. 8. Can an isoquant ever slope upwards? Explain

No.This would mean that if you increased both inputs then ouput would stay the same. Asa general rule,if the fimm has more of all the inputs they can produce more output. 9.Explain the term"marginal rate of technical substitution"? What does a MRTS=4 mean? MRTS is the amount by which the quantity of one input can be reduced when the other input is increased by one unit,while maintaining the same level of output.If the MRTS is 4 then the one i unit and output will be beucdbysthe othersd y on 10.Explain why the marginal rate of technical substitution is likely to diminish as more and more labor is substituted for capital. As the quantities of the inputs are changed the marginal product of each input will change.As more and more labor is added,the marginal product of labor is likely to diminish.Because capital has been reduced,each unit of capital remaining is likely to be more productive.Therefore,more units of labor will be required to replace each unit of capital. Alternatively,as e move down and to the right along an isoquant along which the MRIS is diminishing.we have to give up less capital for each unit of labor added to keep output constant. 11.Diminishing returns to a single factor of production and constant returns to scale are not inconsistent.Discuss. Diminishing returns to a single factor are observable in all production processes at some This fact issope aw of dimn ervasive that economists have named it the rginal pr oduct By definition, marginal productof an input is the additional output generated by employing one more unit of the input all other inputs held fixed.The extra output,or returns,to the single input diminish because all other inputs are held fixed.For example,when holding the level ofcapital constant each additional unit oflabor has less capital to work with. Unlike the returns to a single factor,returns to scale are proportional increases in all inputs.While each facte by itself exhibits diminishing turns,output may more than doubk.than when all the imputa are doubled.The distinction again is that with returns to scale,all inputs are increased in the same proportion and no input is held fixed
No. This would mean that if you increased both inputs then output would stay the same. As a general rule, if the firm has more of all the inputs they can produce more output. 9. Explain the term “marginal rate of technical substitution”? What does a MRTS=4 mean? MRTS is the amount by which the quantity of one input can be reduced when the other input is increased by one unit, while maintaining the same level of output. If the MRTS is 4 then the one input can be reduced by 4 units as the other is increased by one unit and output will be the same. 10. Explain why the marginal rate of technical substitution is likely to diminish as more and more labor is substituted for capital. As the quantities of the inputs are changed the marginal product of each input will change. As more and more labor is added, the marginal product of labor is likely to diminish. Because capital has been reduced, each unit of capital remaining is likely to be more productive. Therefore, more units of labor will be required to replace each unit of capital. Alternatively, as we move down and to the right along an isoquant along which the MRTS is diminishing, we have to give up less capital for each unit of labor added to keep output constant. 11. Diminishing returns to a single factor of production and constant returns to scale are not inconsistent. Discuss. Diminishing returns to a single factor are observable in all production processes at some level of inputs. This fact is so pervasive that economists have named it the “law of diminishing marginal productivity.” By definition, the marginal product of an input is the additional output generated by employing one more unit of the input, all other inputs held fixed. The extra output, or returns, to the single input diminish because all other inputs are held fixed. For example, when holding the level of capital constant, each additional unit of labor has less capital to work with. Unlike the returns to a single factor, returns to scale are proportional increases in all inputs. While each factor by itself exhibits diminishing returns, output may more than double, less than double, or exactly double when all the inputs are doubled. The distinction again is that with returns to scale, all inputs are increased in the same proportion and no input is held fixed

12.Can a firm have a production function that exhibits increasing returns to scale,constant returns to scale,and decreasing returns to scale as output increases?Discuss. Most firms have production functions that exhibit first increasing.then constant and ultimately decreasing returns to scale.At low levels of output,a proportional increase in all inputs may lead to a larger-than-proportional increase in output. based on an increase in the opportunity for each factor to specialize.For exampk and two computers,each peron can ecialize by at they are bes which all double.As the firm grows,the opportunities for pecialization may diminish anda doubling of all inputs will lead to only a doubling of output.When there are constant returns to scale,the firm is replicating what it is already doing.At some level of poduction,thefirm will besolarge that when inputsare doubled,output will less than double,that can arise from management diseconmie 13.Give an aple of a production pro ess in which the short run involves Any small business where one input requires more than a week to change woul be an example.The process of hiring more labor,which requires announcing the position,interviewing applicants,and negotiating terms ofemployment,can take a day.if done through a temporary employment agency.Usually.however.the Expansion,requiring a larger location,will also take longer than a week 二、EXERCISES 1.The menu at Joe's coffee shop consists of a variety of coffee drinks,pastries and sandwiches.The marginal product of an additional worker can be defined as the number of customers that can be served by that worker in a given time odbeen mployinone worker,but is copidering hiringo ain why the product of the and third workers might be higher than the first. Why might you expect the marginal product of additional workers to eventually diminish? The marginal product could well increase for the second and third workers.since each of the first 2 or 3 workers would be able to specialize in a different task.If there is only 1 worker,then that worker will have to take orders and prepare all the food. Eventually,howev er the marginal product would dimin sh bec here would be toc many people behind the counter trying to accomplish a limited number of tasks. 2.Suppose a chair manufacturer is producing in the short run (with its existing plant and equipment).The manufacturer has observed the following levels of production corresponding to different numbers of workers:
12. Can a firm have a production function that exhibits increasing returns to scale, constant returns to scale, and decreasing returns to scale as output increases? Discuss. Most firms have production functions that exhibit first increasing, then constant, and ultimately decreasing returns to scale. At low levels of output, a proportional increase in all inputs may lead to a larger-than-proportional increase in output, based on an increase in the opportunity for each factor to specialize. For example, if there are now two people and two computers, each person can specialize by completing those tasks that they are best at, which allows output to more than double. As the firm grows, the opportunities for specialization may diminish and a doubling of all inputs will lead to only a doubling of output. When there are constant returns to scale, the firm is replicating what it is already doing. At some level of production, the firm will be so large that when inputs are doubled, output will less than double, a situation that can arise from management diseconomies. 13. Give an example of a production process in which the short run involves a day or a week and the long run any period longer than a week. Any small business where one input requires more than a week to change would be an example. The process of hiring more labor, which requires announcing the position, interviewing applicants, and negotiating terms of employment, can take a day, if done through a temporary employment agency. Usually, however, the process takes a week or more. Expansion, requiring a larger location, will also take longer than a week. 二、EXERCISES 1. The menu at Joe’s coffee shop consists of a variety of coffee drinks, pastries, and sandwiches. The marginal product of an additional worker can be defined as the number of customers that can be served by that worker in a given time period. Joe has been employing one worker, but is considering hiring a second and a third. Explain why the marginal product of the second and third workers might be higher than the first. Why might you expect the marginal product of additional workers to eventually diminish? The marginal product could well increase for the second and third workers, since each of the first 2 or 3 workers would be able to specialize in a different task. If there is only 1 worker, then that worker will have to take orders and prepare all the food. Eventually, however, the marginal product would diminish because there would be too many people behind the counter trying to accomplish a limited number of tasks. 2. Suppose a chair manufacturer is producing in the short run (with it s existing plant and equipment). The manufacturer has observed the following levels of production corresponding to different numbers of workers:

Number ofchairs Number ofworkers 18 24 45 28 7 6 a.Calculate the marginal and average product of labor for this production function. The verage poduct ofutThemargnal product of AO labor,MP,is equal to the change in output divided by the change in AL labor input.For this production process we have: Q APL MP 0 0 1 10 0 2 18 9 8 3 24 6 4 28 4 5 30 6 2 28 4.7 -2 7 25 3.6 -3 b.Does this production function exhibit diminishing returns to labor?Explain This production proces exhibits diminishingetu s to labor.The marginal product of labor,the extra output produced by each additional worker,diminishes as workers are added,and is actually negative for the sixth and seventh workers. c.Explain intuitively what might cause the marginal product oflabor to become negative
Number of chairs Number of workers 1 10 2 18 3 24 4 28 5 30 6 28 7 25 a. Calculate the marginal and average product of labor for this production function. The average product of labor, APL, is equal to Q L . The marginal product of labor, MPL, is equal to Q L , the change in output divided by the change in labor input. For this production process we have: L Q APL MPL 0 0 _ _ 1 10 10 10 2 18 9 8 3 24 8 6 4 28 7 4 5 30 6 2 6 28 4.7 -2 7 25 3.6 -3 b. Does this production function exhibit diminishing returns to labor? Explain. This production process exhibits diminishing returns to labor. The marginal product of labor, the extra output produced by each additional worker, diminishes as workers are added, and is actually negative for the sixth and seventh workers. c. Explain intuitively what might cause the marginal product of labor to become negative
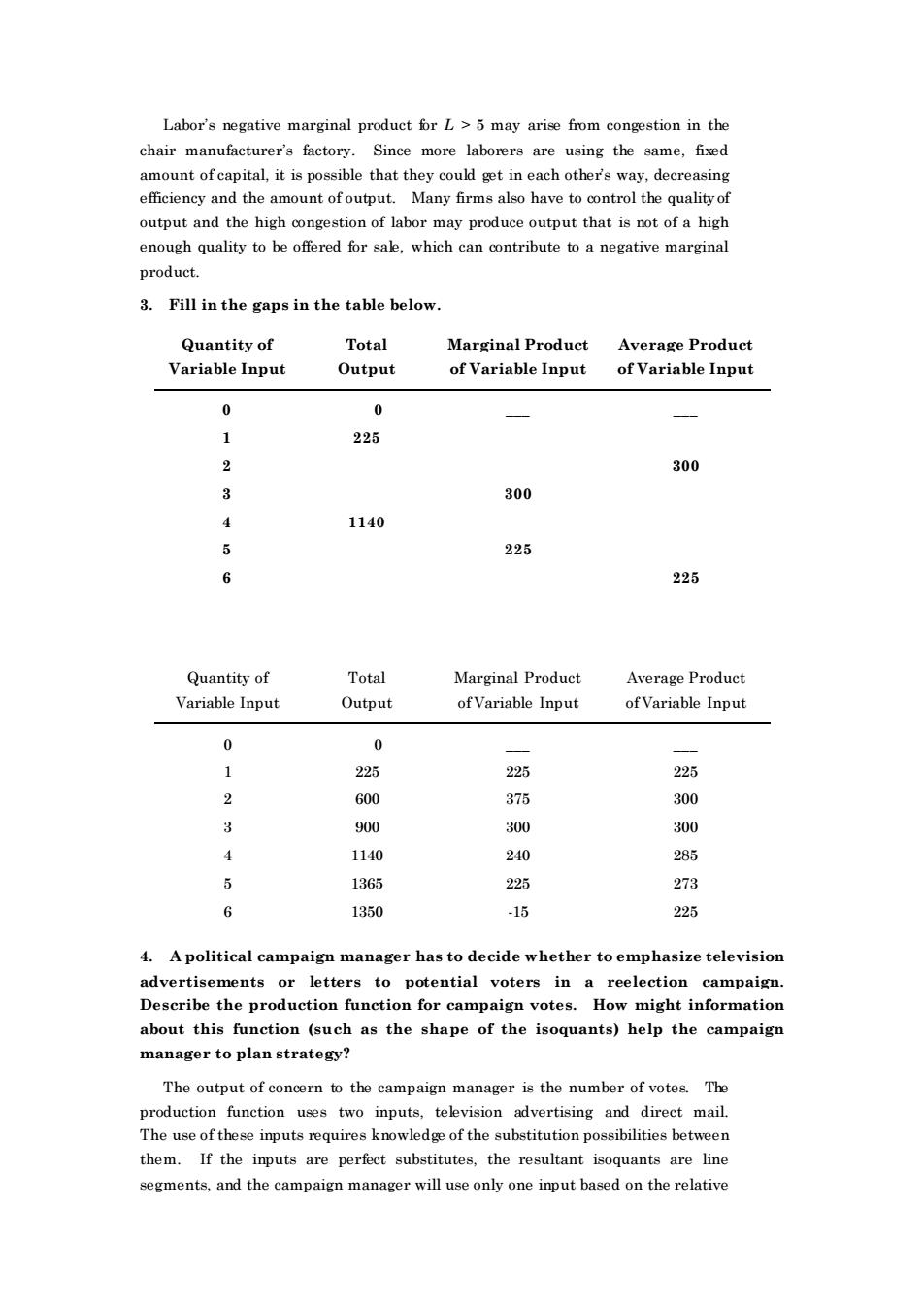
Labor's negative marginal product for L>5 may arise from congestion in the chair manufacturer's factory Since more laborers using the amount of eapital,tis possbe that othe way,decreasing efficiency and the amount ofoutput. Many firms also have to control the quality o output and the high congestion of labor may produce output that is not of a high enough quality to be offered for sale,which can contribute to a negative marginal product. 3.Fill in the gaps in the table below Quantity of Total Marginal Product Average Product Variable Input Output of Variable Input of Variable Input 0 1 225 2 300 3 300 4 1140 5 225 6 225 Quantity of Total Marginal Product Average Product Variable Input Output of Variable Input of Variable Input 0 0 1 225 225 225 2 600 375 300 3 900 300 300 4 1140 2 285 1365 25 273 6 1350 -15 225 4.A political campaign manager has to decide whether to emphasize television ements or letters to in a reelec tion campa a votes. about this function (such as the shape of the isoquants)help the campaign manager to plan strategy? The output of concern to the campaign manager is the number of votes.The production function uses two inputs,television advertising and direct mail. The use of these inputs requires knowledge of the substitution possibilities between them.If the inputs are perfect substitutes,the resultant isoquants are line segments,and the campaign manager will use only one input based on the relative
Labor’s negative marginal product for L > 5 may arise from congestion in the chair manufacturer’s factory. Since more laborers are using the same, fixed amount of capital, it is possible that they could get in each other’s way, decreasing efficiency and the amount of output. Many firms also have to control the quality of output and the high congestion of labor may produce output that is not of a high enough quality to be offered for sale, which can contribute to a negative marginal product. 3. Fill in the gaps in the table below. Quantity of Variable Input Total Output Marginal Product of Variable Input Average Product of Variable Input 0 0 _ _ 1 225 2 300 3 300 4 1140 5 225 6 225 Quantity of Variable Input Total Output Marginal Product of Variable Input Average Product of Variable Input 0 0 _ _ 1 225 225 225 2 600 375 300 3 900 300 300 4 1140 240 285 5 1365 225 273 6 1350 -15 225 4. A political campaign manager has to decide whether to emphasize television advertisements or letters to potential voters in a reelection campaign. Describe the production function for campaign votes. How might information about this function (such as the shape of the isoquants) help the campaign manager to plan strategy? The output of concern to the campaign manager is the number of votes. The production function uses two inputs, television advertising and direct mail. The use of these inputs requires knowledge of the substitution possibilities between them. If the inputs are perfect substitutes, the resultant isoquants are line segments, and the campaign manager will use only one input based on the relative

prices If the inpuareopereetbtitute theill have shape.The campaign manager will then use acombination of the two inputs 5.For each of the following examples,draw a representative isoquant. What can you say about the marginal rate of technical substitution in each case? a.A firm can hire only full-time employees to produce its output,or it can hire some combination of full-time and part-time employees.For each full-time worker let go.the firm must hire an increasing number of temporary employees to maintain the same level of output. Place part time workers on the vertical axis and full time workers on the horizontal lope the isoquan t meas ures he nu of part time workers that can be exchanged for a full time worker,while still maintaining output. Wher we are at the bottom end of the isoquant we have a lot of full time workers and few part time workers.As we move up the isoquant and give up full time workers.we must hire more and more part time v workers to replace each full time worker.The slope increases(in abs mms)as we mo up the isoquan The isoquan is therefore convex and we have diminishing marginal rate of technical substitution. b.A firm finds they it can always trade two units of labor for one unit of capital and still keep output constant. The marginal rate of technical substitution measures the number of units of labor that can be exchanged for a unit of capital while still maintaining output.If the firm can always trade two labor for one capital then the MRTS is constant and the isoquant is linea c.A firm require s exactly two full-time workers to operate each piece of machinery in the factory. This firm operates under a fixed proportions technology,and the isoquants are L-shaped.The firm cannot exchange any labor for capital and still maintain output because it must maintain a fixed 2:1 ratio of laborcapital. 6.A firm has a production process in which the inputs to production are perfeetly substitutable in the long run.Can you tel whether the marginal rate of technical substitution is high or low,or is further info ormation necessary? Discuss
prices. If the inputs are not perfect substitutes, the isoquants will have a convex shape. The campaign manager will then use a combination of the two inputs. 5. For each of the following examples, draw a representative isoquant. What can you say about the marginal rate of technical substitution in each case? a. A firm can hire only full-time employees to produce its output, or it can hire some combination of full-time and part-time employees. For each full-time worker let go, the firm must hire an increasing number of temporary employees to maintain the same level of output. Place part time workers on the vertical axis and full time workers on the horizontal axis. The slope of the isoquant measures the number of part time workers that can be exchanged for a full time worker, while still maintaining output. When we are at the bottom end of the isoquant we have a lot of full time workers and few part time workers. As we move up the isoquant and give up full time workers, we must hire more and more part time workers to replace each full time worker. The slope increases (in absolute value terms) as we move up the isoquant. The isoquant is therefore convex and we have diminishing marginal rate of technical substitution. b. A firm finds they it can always trade two units of labor for one unit of capital and still keep output constant. The marginal rate of technical substitution measures the number of units of labor that can be exchanged for a unit of capital while still maintaining output. If the firm can always trade two labor for one capital then the MRTS is constant and the isoquant is linear. c. A firm requires exactly two full-time workers to operate each piece of machinery in the factory. This firm operates under a fixed proportions technology, and the isoquants are L-shaped. The firm cannot exchange any labor for capital and still maintain output because it must maintain a fixed 2:1 ratio of labor:capital. 6. A firm has a production process in which the inputs to production are perfectly substitutable in the long run. Can you tell whether the marginal rate of technical substitution is high or low, or is further information necessary? Discuss

The marginal rate of technical substitution.MRTS.is the absolute value of the slope of an.If the inputs are perfct substitutes,the quantswill b linear.To caleulate the sbpe of the isoquant,and hence the MRTSwe needto know the rate at which one input may be substituted for the other.In this case,we do not know whether the MRTS is high or low.All we know is that it is a constant number.We need to know the marginal product of each input to determine the MRTS. 7.The mar ginal product of labor in the is 50 chips per r ho r.The arginal r of technical urs oflabor for hours of machine-capital is 1/4.What is the marginal product of capital? The marginal rate of technical substitution is defined at the ratio of the tw marginal products.Here,we are given the marginal product of labor and the marginal rate of technical substitution.To determine the marginal product of and the } or MPK=200 computer chips per hour. 8.Do the following functions exhibit increasing,constant,or decreasing returns to scale?What happens to the marginal product of each individual factor as that factor is increased,and the other factor is held constant? g=3L+2K This function exhibits onant scale For example.if s2andKis the g is 10.IfL is 4 and K is 4 ther w double. 9s20 When the inpu doubled.o p Each marginal product is constant for this production function. L increases by I q will increase by 3.When K increases by I q will increase by 2. b. 9=(2L+2K月 This function exhibits decreasing returns to scale.For example,if L is 2 and K is 2 then q is 2.8.IfL is 4 and K is 4 thenq is 4.When the inputs are doubled,output will less than double.The marginal asing This can be determined using calculus by differentiating the production functior with respect to either input,while holding the other input constant.For example,the marginal product of labor is 2 d2L+20 Since L is in the de product gets smaller If you do not kr now ca Iculus nen you can choo e severa I values forL,find q(fo some fixed value of K),and then find the marginal product.For example,if L=4 and
The marginal rate of technical substitution, MRTS, is the absolute value of the slope of an isoquant. If the inputs are perfect substitutes, the isoquants will be linear. To calculate the slope of the isoquant, and hence the MRTS, we need to know the rate at which one input may be substituted for the other. In this case, we do not know whether the MRTS is high or low. All we know is that it is a constant number. We need to know the marginal product of each input to determine the MRTS. 7. The marginal product of labor in the production of computer chips is 50 chips per hour. The marginal rate of technical substitution of hours of labor for hours of machine-capital is 1/4. What is the marginal product of capital? The marginal rate of technical substitution is defined at the ratio of the two marginal products. Here, we are given the marginal product of labor and the marginal rate of technical substitution. To determine the marginal product of capital, substitute the given values for the marginal product of labor and the marginal rate of technical substitution into the following formula: MP MP MRTS, MP L K K = or = 50 1 4 , or MPK = 200 computer chips per hour. 8. Do the following functions exhibit increasing, constant, or decreasing returns to scale? What happens to the marginal product of each individual factor as that factor is increased, and the other factor is held constant? a. q = 3L + 2K This function exhibits constant returns to scale. For example, if L is 2 and K is 2 then q is 10. If L is 4 and K is 4 then q is 20. When the inputs are doubled, output will double. Each marginal product is constant for this production function. When L increases by 1 q will increase by 3. When K increases by 1 q will increase by 2. b. q = (2L + 2K) 1 2 This function exhibits decreasing returns to scale. For example, if L is 2 and K is 2 then q is 2.8. If L is 4 and K is 4 then q is 4. When the inputs are doubled, output will less than double. The marginal product of each input is decreasing. This can be determined using calculus by differentiating the production function with respect to either input, while holding the other input constant. For example, the marginal product of labor is q L = 2 2(2L + 2K) 1 2 . Since L is in the denominator, as L gets bigger, the marginal product gets smaller. If you do not know calculus, then you can choose several values for L, find q (for some fixed value of K), and then find the marginal product. For example, if L=4 and

K=4 then q=4.IfL=5 and K=4then q=4.24.If L=6 and K=4 then q=4.47 Marginal product of labor falls from 24 to.23 9-3K2 This function exhibits increasing returns to scale.For example,ifL is 2 and K is 2 then q is 24.If L is 4 and K is 4 then q is 192.When the inputs are doubled, output will more than double.notice also that if we increase each input by the same factor then we get the following q=3L0)2=23LK2=g Since is raised to a power greater than 1,we have increasing retums to scale The marginal product of labor is constant and the marginal product of capital is ne cacth erer o capital is MPK=2*3*L*K.As K increases,MPK will increase.If you do not know calculus then you can fix the value of L,choose a starting value for K,and find q. Now increase K by 1 unit and find the newq.Do this a few more times s and you can calculate marginal product.This was done in part b above,and is done in part d below. d. 9=K This function exhibits constant returns to scale.For example,if L is 2 and K is2 When the inputs are edoubled.ou if we increase each input by the same factor then we get the following: q4=(L)(2K)产=LK= Since A is raised to the power 1,we have constant retumns to scale. The marginal product of labor is decreasing and the marginal product of capital is decreasing.Using calculus,the marginal product of capital is For any given value ofL,as K increases,MPK will increase. Ifyou do not know n you can fix the value of L,ch sta lue for k and find a Let L=for example. If K is 4 then q is 4,if K is 5 then q is 4.47,and ifK is 6 the q is 4.89.The marginal product of the 5th unit ofK is 4.47-4=0.47,and the marginal product of the 6th unit of K is 4.89-4.47=0.42.Hence we have diminishing marginal product of capital.You can do the same thing for the marginal product of labor. e.9=42+4K
K=4 then q=4. If L=5 and K=4 then q=4.24. If L=6 and K=4 then q= 4.47. Marginal product of labor falls from 0.24 to 0.23. c. q = 3LK 2 This function exhibits increasing returns to scale. For example, if L is 2 and K is 2 then q is 24. If L is 4 and K is 4 then q is 192. When the inputs are doubled, output will more than double. Notice also that if we increase each input by the same factor then we get the following: q' = 3(L)(K) 2 = 3 3LK2 = 3 q . Since is raised to a power greater than 1, we have increasing returns to scale. The marginal product of labor is constant and the marginal product of capital is increasing. For any given value of K, when L is increased by 1 unit, q will go up by 3K 2 units, which is a constant number. Using calculus, the marginal product of capital is MPK=2*3*L*K. As K increases, MPK will increase. If you do not know calculus then you can fix the value of L, choose a starting value for K, and find q. Now increase K by 1 unit and find the new q. Do this a few more times and you can calculate marginal product. This was done in part b above, and is done in part d below. d. q = L 1 2K 1 2 This function exhibits constant returns to scale. For example, if L is 2 and K is 2 then q is 2. If L is 4 and K is 4 then q is 4. When the inputs are doubled, output will exactly double. Notice also that if we increase each input by the same factor then we get the following: q' = (L) 1 2 (K) 1 2 = L 1 2K 1 2 = q . Since is raised to the power 1, we have constant returns to scale. The marginal product of labor is decreasing and the marginal product of capital is decreasing. Using calculus, the marginal product of capital is . For any given value of L, as K increases, MPK will increase. If you do not know calculus then you can fix the value of L, choose a starting value for K, and find q. Let L=4 for example. If K is 4 then q is 4, if K is 5 then q is 4.47, and if K is 6 then q is 4.89. The marginal product of the 5th unit of K is 4.47-4=0.47, and the marginal product of the 6th unit of K is 4.89-4.47=0.42. Hence we have diminishing marginal product of capital. You can do the same thing for the marginal product of labor. e. q = 4L 1 2 + 4K

This function exhibits decreasing retums to scale.For example,if L is 2 and K is 2 then q is 13.66.IfL is 4 and K is 4 thenq is 24. When the inputs are doubled output will less than double The marginal product of labor is decreasing and the marginal product of capital is constant.For any given value of L,when K is increased by 1 unit,q will go up by 4 units,which is a constant number.To see that the marginal product of labor is decreasing,fix K=1 and choose values for L.If L=1 then q=8,if L=2 then q=9.65, -13.The marginal product ofthe se Marginal product of labor is diminishing. 9.The produetion function for the personal computers of DISK,Ine.,is given by q=10KasLas,where q is the number ofcomputers produced per day,K is hours of machine time,and Lis hours of labor input.DISK's competitor,FLOPPY,Inc.,is using the production function g=10K0.6Lo4. a.If both companies use the same amounts of capital and labor,which will generate more output? Let Q be the output of DISK.Inc.g2.be the output of FLOPPY.Inc.and Xbe the same equal amounts ofeapital and labor for the two firms.to thei production functions, g=100.5X05=100.5+0.5=10X and =10604=10X0.6+00=10K Because g =g both firms generate the same output with the same inputs Note that if the two firms both sed the same amount of capital and the amount of labor,but the amount of capital was not equal to the amount of labor then the two firms woul not produce the same level of output.In fact,if K>L then q>q. b.Assume that capital is limited to 9 machine hours but labor is unlimited in supply.In which company is the marginal product of labor greater? Explain. 0Todetermine the production function with thehigh marginal productivity of labor,consider the following table: MPr MPL Firm】 Firm2 Firm 2 0 00 0.00 1 30.00 30.00 37.37 37.37 2 42.43 12.43 49.31 1194 3 51.96 93 58.00 8.69
This function exhibits decreasing returns to scale. For example, if L is 2 and K is 2 then q is 13.66. If L is 4 and K is 4 then q is 24. When the inputs are doubled, output will less than double. The marginal product of labor is decreasing and the marginal product of capital is constant. For any given value of L, when K is increased by 1 unit, q will go up by 4 units, which is a constant number. To see that the marginal product of labor is decreasing, fix K=1 and choose values for L. If L=1 then q=8, if L=2 then q=9.65, and if L=3 then q=10.93. The marginal product of the second unit of labor is 9.65-8=1.65 and the marginal product of the third unit of labor is 10.93-9.65=1.28. Marginal product of labor is diminishing. 9. The production function for the personal computers of DISK, Inc., is given by q = 10K0.5L0.5, where q is the number of computers produced per day, K is hours of machine time, and L is hours of labor input. DISK’s competitor, FLOPPY, Inc., is using the production function q = 10K0.6L0.4. a. If both companies use the same amounts of capital and labor, which will generate more output? Let Q be the output of DISK, Inc., q2 , be the output of FLOPPY, Inc., and X be the same equal amounts of capital and labor for the two firms. Then, according to their production functions, q = 10X0.5X0.5 = 10X(0.5 + 0.5) = 10X and q2 = 10X0.6X0.4 = 10X(0.6 + 0.4) = 10X. Because q = q2 , both firms generate the same output with the same inputs. Note that if the two firms both used the same amount of capital and the same amount of labor, but the amount of capital was not equal to the amount of labor, then the two firms would not produce the same level of output. In fact, if K>L then q2>q. b. Assume that capital is limited to 9 machine hours but labor is unlimited in supply. In which company is the marginal product of labor greater? Explain. With capital limited to 9 machine units, the production functions become q = 30L0.5 and q2 = 37.372L0.4. To determine the production function with the highest marginal productivity of labor, consider the following table: L q Firm 1 MPL Firm 1 q Firm 2 MPL Firm 2 0 0.0 _ 0.00 _ 1 30.00 30.00 37.37 37.37 2 42.43 12.43 49.31 11.94 3 51.96 9.53 58.00 8.69