广东工业大学：《土力学》课程教学资源（课件讲稿）第6章 土压力 6.2 朗肯（Rankine）土压力理论

第6章土压力 主讲：刘勇健 广东工业大学Guangdong University of Technology

第6章 土压力 广 东 工 业 大 学 Guangdong University of Technology 主讲：刘勇健

§6.2 朗肯(Rank i ne)土压力理论 William John Maquorn Rankine (1820-1872)

§6.2 朗肯(Rankine)土压力理论

朗肯土压力计算 第二节朗肯土压力理论 基本假定 (1)挡土墙是刚性的，墙背光滑竖直； N (2)填土面水平，填土处于极限平衡状态； (③)墙背光滑，不计填土与墙背间摩擦力。 ·由于某种原因，处于极限平衡状态

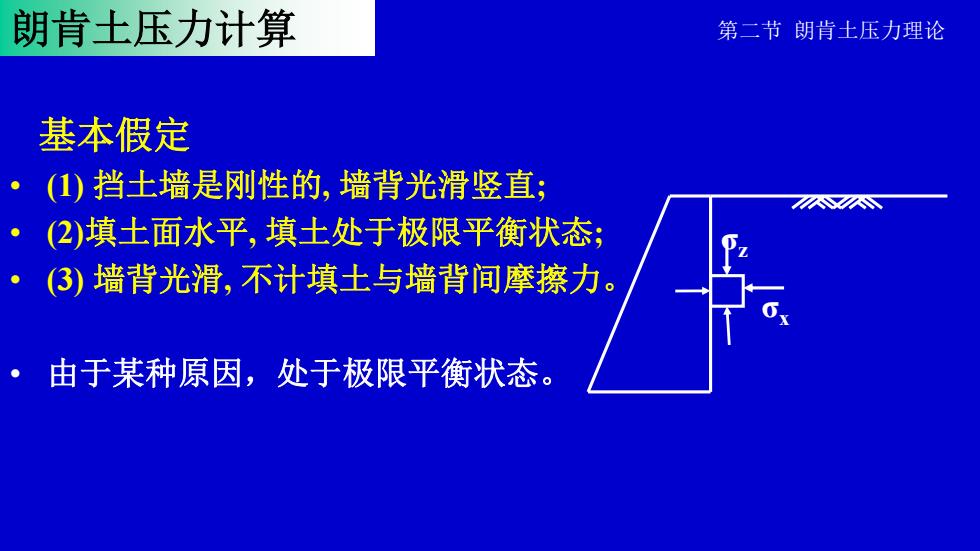
朗肯土压力计算 第二节 朗肯土压力理论 基本假定 • (1) 挡土墙是刚性的, 墙背光滑竖直; • (2)填土面水平, 填土处于极限平衡状态; • (3) 墙背光滑, 不计填土与墙背间摩擦力。 • 由于某种原因，处于极限平衡状态。 σz σx

朗肯土压力理论基本条件和假定 条件 墙背光滑 墙背垂直 填土表面水平 假设 墙后各点均处于极限平衡状态

朗肯土压力理论基本条件和假定 条件 墙背光滑 墙背垂直 填土表面水平 假设 墙后各点均处于极限平衡状态

朗肯土压力的计算 第二节朗肯土压力理论 主动土压力： 挡土墙离开填土移动，土体 成拉伸趋势。 竖向自重应力不变，而水平 向应力不断减小，土体达到极限 平衡状态，形成一系列滑裂面， 45+φ/2 称主动朗肯状态。 @

朗肯土压力的计算 • 主动土压力： • 挡土墙离开填土移动，土体 成拉伸趋势。 • 竖向自重应力不变，而水平 向应力不断减小，土体达到极限 平衡状态，形成一系列滑裂面， 称主动朗肯状态。 450+φ／２ 第二节 朗肯土压力理论 O   强度包线 x z

朗肯主动极限平衡状态 半无限土体内各点的应力：从弹性平衡状态发展为 极限平衡状态的情况。 极限莫尔圆：O1,竖向自重应力，心3，主动土压力 O,-YZ

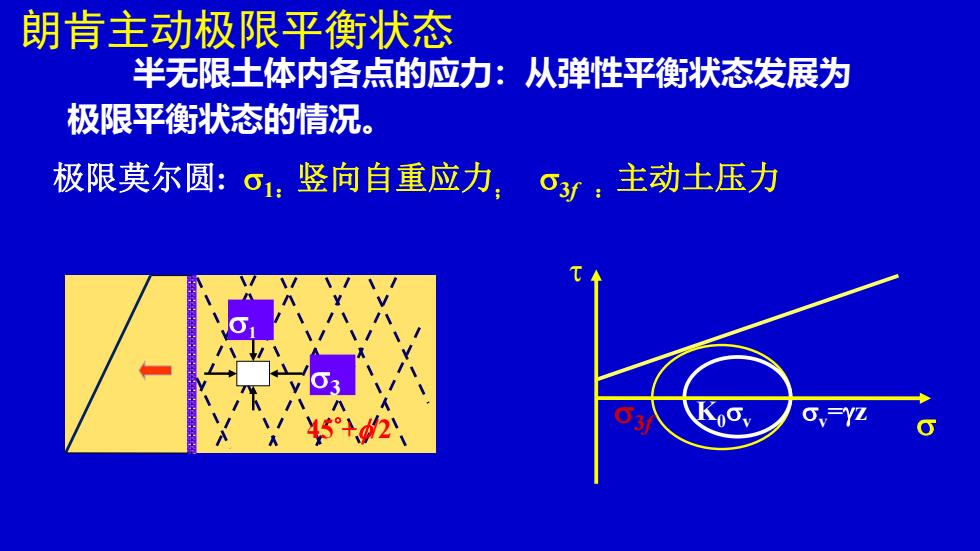
朗肯主动极限平衡状态 3f v=z  K0v 1 3 45+f/2  极限莫尔圆: 1：竖向自重应力； 3f ：主动土压力 半无限土体内各点的应力：从弹性平衡状态发展为 极限平衡状态的情况

朗肯主动土压力的计算 第二节朗肯土压力理论 朗肯主动土压力强度为： 对黏性土： a,=7ztan459-号》-2ctan(450-2)=7eK.-2eK 2 对无黏性土： oa=y2tan2(450- 3=k 主动土压力系数： K.tan'(4-2)

朗肯主动土压力的计算 • 朗肯主动土压力强度为： 对黏性土： 2 0 0 a a a tan (45 ) 2 tan(45 ) 2 2 2 z c zK c K      = = － － － － 对无黏性土： 2 0 a a tan (45 ) 2 z zK     = = － 2 0 a tan (45 ) 2 K  = － 第二节 朗肯土压力理论 主动土压力系数：

朗肯主动土压力 填土为砂土(=0) 6 主动土压力：O。=2K。 (kPa) 主动土压力系数：K。=tan(45°-p/2) 土压力分布：沿墙高呈三角形分布 合力： E。=1/2K。P (kN/m) H/3 作用点： 底部以上H/3处 滑裂面方向：与水平夹角45°+0/2 yHKa

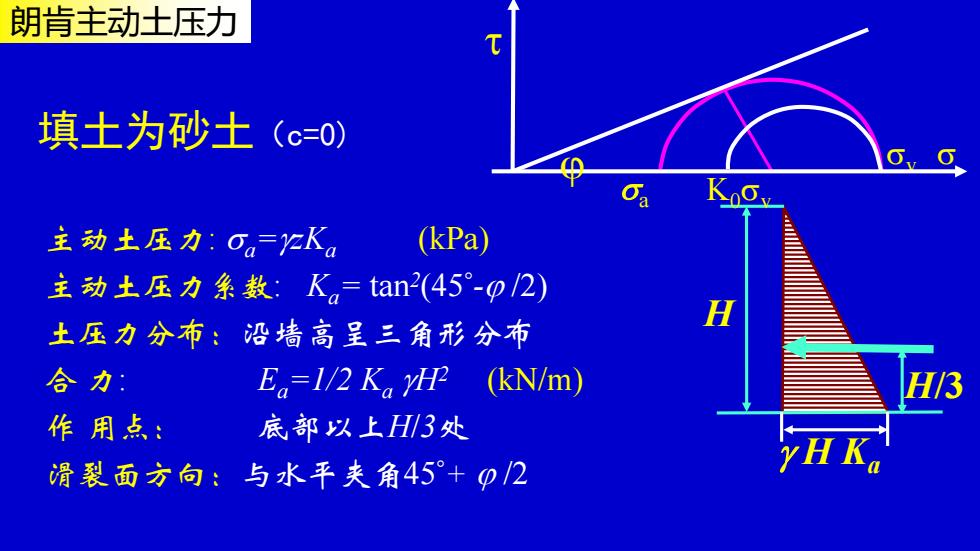
朗肯主动土压力 主动土压力: a =zKa (kPa) 主动土压力系数: Ka= tan2 (45 - /2) 土压力分布：沿墙高呈三角形分布 合 力: Ea=1/2 Ka H2 (kN/m) 作 用点： 底部以上H/3处 滑裂面方向：与水平夹角45+  /2 填土为砂土（c=0) H H/3  H Ka a K0v v   

朗肯主动土压力的计算 第二节朗肯土压力理论 黏性土：主动土压力强度由两部分组成： o。=y=tan2(450- 2-28450多=7k,20V Zo yHK a

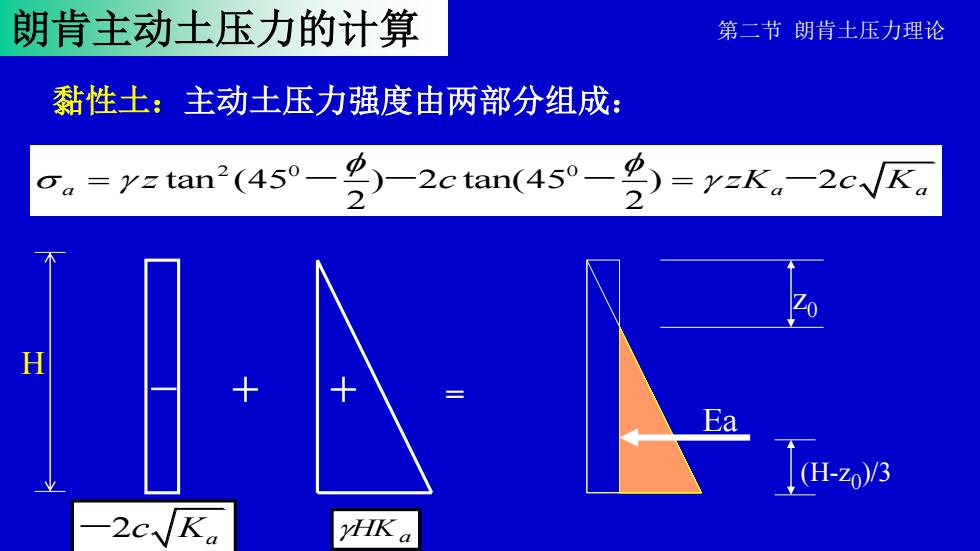
朗肯主动土压力的计算 黏性土：主动土压力强度由两部分组成： Ea (H-z0 )/3 ＋ ＋ = HKa － －2c Ka z0 第二节 朗肯土压力理论 2 0 0 tan (45 ) 2 tan(45 ) 2 2 2 a a a z c zK c K f f    = = － － － － H

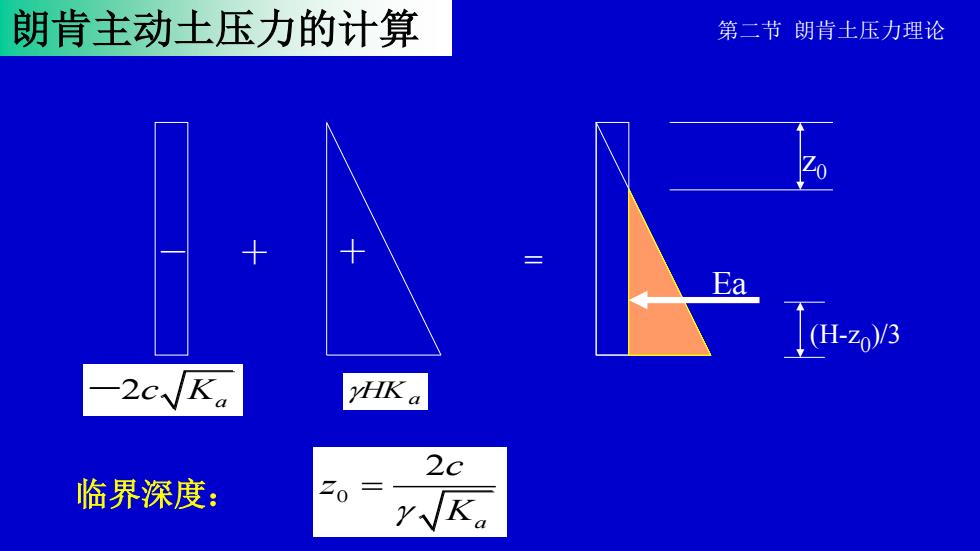
朗肯主动土压力的计算 第二节朗肯土压力理论 Ea 2cKa yHK a 2c 临界深度： Zo Y Ka

朗肯主动土压力的计算 临界深度： Ea ＋ ＋ = HKa － －2c Ka z0 0 2 a c z  K = (H-z0 )/3 第二节 朗肯土压力理论