
"Solid State Physics I"Course Syllabus 1,General information Course Title Solid State PhysicsI PHYS3110 Course Category Major Core Majors Physics Total Hours 4credits Lecture 72 Hours Hours Instructor Wang Xue Feng Date 2021.9 Textbook Charles Kittel,Introduction to Solid State Physics(Wiley:New York,2004). 2、Course Aim (1)General Aim Solid State Physics I is a basic course of Applied Physics.The subject focuses on the relationship between the solid microstructure and particles and the law of their motion.The subject llustrates the and theory and band heory Crysta ding of solid ttice ibration,Elec energy band Electron dynamies in sod (2)Specifications: Course Aim 1:Be aware of the history and evolution of Solid State Physics:Important Course Aim 2:Grasp the fundamental principles and methods of Solid State Physics.Know well the Categories of crystals according to their geometry,atomic bindings and electronic structures.Be capable of estimating crystal properties according to their categories. Course Aim3:Master the analytical methods used in Solid State Physics,Master the method to calculate the binding energies.the phonon spectra,the electronic energy structures of typical crystals.Be capable of analyzing the transport properties of typical crystals and figuring out the electronic motion in electric field
“Solid State Physics I” Course Syllabus 1、General information Course Title Solid State Physics I Course Code PHYS3110 Course Category Major Core Majors Physics Total Hours 4 credits Lecture Hours 72 Hours Instructor Wang Xue Feng Date 2021.9 Textbook Charles Kittel, Introduction to Solid State Physics (Wiley: New York, 2004). 2、Course Aim (1) General Aim: Solid State Physics I is a basic course of Applied Physics. The subject focuses on the relationship between the solid microstructure and particles and the law of their motion. The subject illustrates the solid properties and application, especially solid state theory and band theory. The topics include: Crystal structure, Binding of solid, Lattice vibration, Electronic energy band, Electron dynamics in solid. (2) Specifications: Course Aim 1: Be aware of the history and evolution of Solid State Physics; Important developments and applications in other science and technology communities, such as materials, nanotechnologies, and electronics; and the scope of application. Course Aim 2: Grasp the fundamental principles and methods of Solid State Physics. Know well the Categories of crystals according to their geometry, atomic bindings and electronic structures. Be capable of estimating crystal properties according to their categories. Course Aim 3: Master the analytical methods used in Solid State Physics, Master the method to calculate the binding energies, the phonon spectra, the electronic energy structures of typical crystals. Be capable of analyzing the transport properties of typical crystals and figuring out the electronic motion in electric field
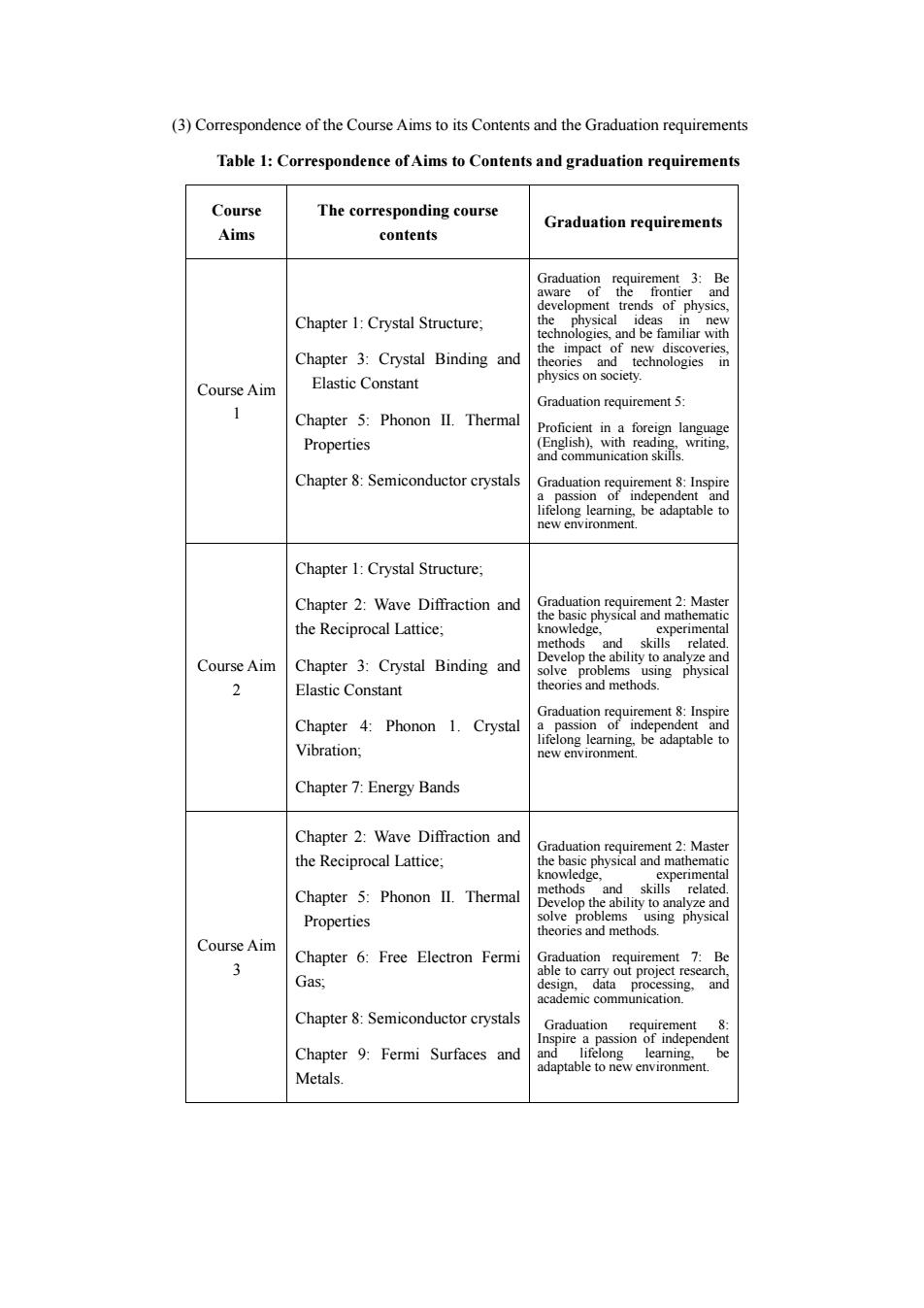
(3)Correspondence of the Course Aims to its Contents and the Graduation requirements Table 1:Correspondence of Aims to Contents and graduation requirements Course The corresponding course Graduation requirements Aims contents Chapter 1:Crystal Structure; the hn Chapter 3:Crystal Binding and Course Aim Elastic Con Graduation requirement 5: 1 Chapter 5:Phonon II.Thermal Properties Chapter 8:Semiconductor crystals Chapter 1:Crystal Structure: Chapter 2:Wave Diffraction and the Reciprocal Lattice. 2 Course Aim Chapter 3:Crystal Binding and 2 Elastic Constant Chapter 4:Phonon 1.Crystal Vibration; Chapter 7:Energy Bands Chapter 2:Wave Diffraction and the Reciprocal Lattice Chapter 5:Phonon II.Thermal Properties Course Aim 3 Chapter 6:Free Electron Ferm t 7:Be Gas and Chapter:Semiconductor crystals Graduation Chapter 9:Fermi Surfaces and Metals
(3) Correspondence of the Course Aims to its Contents and the Graduation requirements Table 1: Correspondence of Aims to Contents and graduation requirements Course Aims The corresponding course contents Graduation requirements Course Aim 1 Chapter 1: Crystal Structure; Chapter 3: Crystal Binding and Elastic Constant Chapter 5: Phonon II. Thermal Properties Chapter 8: Semiconductor crystals Graduation requirement 3: Be aware of the frontier and development trends of physics, the physical ideas in new technologies, and be familiar with the impact of new discoveries, theories and technologies in physics on society. Graduation requirement 5: Proficient in a foreign language (English), with reading, writing, and communication skills. Graduation requirement 8: Inspire a passion of independent and lifelong learning, be adaptable to new environment. Course Aim 2 Chapter 1: Crystal Structure; Chapter 2: Wave Diffraction and the Reciprocal Lattice; Chapter 3: Crystal Binding and Elastic Constant Chapter 4: Phonon 1. Crystal Vibration; Chapter 7: Energy Bands Graduation requirement 2: Master the basic physical and mathematic knowledge, experimental methods and skills related. Develop the ability to analyze and solve problems using physical theories and methods. Graduation requirement 8: Inspire a passion of independent and lifelong learning, be adaptable to new environment. Course Aim 3 Chapter 2: Wave Diffraction and the Reciprocal Lattice; Chapter 5: Phonon II. Thermal Properties Chapter 6: Free Electron Fermi Gas; Chapter 8: Semiconductor crystals Chapter 9: Fermi Surfaces and Metals. Graduation requirement 2: Master the basic physical and mathematic knowledge, experimental methods and skills related. Develop the ability to analyze and solve problems using physical theories and methods. Graduation requirement 7: Be able to carry out project research, design, data processing, and academic communication. Graduation requirement 8: Inspire a passion of independent and lifelong learning, be adaptable to new environment

3,Teaching Targets and Approaches Chapter 1 Crystal Strueture 1.Teaching Aim In this chapter students study the basic concepts and methods to describe crystals.Students familiar ith the Bravais Latticeand Primitive Vector Simple,Body-Centered,and Face-Centered Cubic Lattices,Primitive Unit Cell,Wigner-Seit Cell,and Conventional Cell:Crystal Structures and Lattices with Bases.Symmetry Operations Lattice Planes,and Miller Indices.Students should know how to Classify Bravais Lattices and understand the Seven Crystal Systems and Fourteen Bravais Lattices.Using the basic concepts they Hexonalos-Packed and Diamond Structures Sodium Chloride,Cesium Chloride,and Zineblende Structures 2.Difficult Points Bravais Lattice and Primitive Vectors;Symmetry Operations;Miller Indices 3.Teaching Contents Section 1.Periodic Array of Atoms (1)Lattice Translation Vectors Key points:Understand translation symmetry and know how to find the lattice translation vectors of acrystal Grasp the eoncepts basis and the crystal structure.Know how to find the (2)Fundamental Type of Lattices Key points:Know the two-dimensional lattice types and the three-dimensional lattice types. (3)Index Systems for Crystal Planes Key points:Know how to find out the Miller Indices of a given crystal lattice Section 2.Fundamental Types of Lattices (1)Two-Dimensional Lattice types Key points:Understand the classification of lattice types of two-dimensional crystals (2)Three-Dimensional Lattice types Key points:Understand the classification of lattice types of three-dimensional crystals. Section 3.Index Systems for Crystal Planes Key points:Understand the index systems for erystal planes using primitive lattice vecto coordination and conventional lattice vector coordination systems.Be familiar with the Miller Index system
3、Teaching Targets and Approaches Chapter 1 Crystal Structure 1.Teaching Aim In this chapter students study the basic concepts and methods to describe crystals. Students are required to be familiar with the concepts including Bravais Lattice and Primitive Vectors; Simple, Body-Centered, and Face-Centered Cubic Lattices; Primitive Unit Cell, Wigner-Seitz Cell, and Conventional Cell; Crystal Structures and Lattices with Bases; Symmetry Operations; Lattice Planes, and Miller Indices. Students should know how to Classify Bravais Lattices and understand the Seven Crystal Systems and Fourteen Bravais Lattices. Using the basic concepts, they can identify typical crystal structures such s Hexagonal Close-Packed and Diamond Structures; Sodium Chloride, Cesium Chloride, and Zincblende Structures. 2.Difficult Points Bravais Lattice and Primitive Vectors; Symmetry Operations; Miller Indices 3. Teaching Contents Section 1. Periodic Array of Atoms (1) Lattice Translation Vectors Key points: Understand translation symmetry and know how to find the lattice translation vectors of a crystal. Grasp the concepts basis and the crystal structure. Know how to find the primitive lattice cell of a crystal. (2) Fundamental Type of Lattices Key points: Know the two-dimensional lattice types and the three-dimensional lattice types. (3) Index Systems for Crystal Planes Key points: Know how to find out the Miller Indices of a given crystal lattice. Section 2. Fundamental Types of Lattices (1) Two-Dimensional Lattice types Key points: Understand the classification of lattice types of two-dimensional crystals. (2) Three-Dimensional Lattice types Key points: Understand the classification of lattice types of three-dimensional crystals. Section 3. Index Systems for Crystal Planes Key points: Understand the index systems for crystal planes using primitive lattice vector coordination and conventional lattice vector coordination systems. Be familiar with the Miller Index system

Section 4.Simple Crystal Structures (1)Sodium Chloride Structure Key points:Be familiar with the Sodium Chloride Structure.Know how to figure out the corresponding lattice structure,primitive cells,basis,and lattice type. (2)Cesium Chloride Structure Key points:Be familiar with the Cesium Chloride Structure.Know how to figure ou the corresponding lattice structure,primitive cells,basis,and lattice type. (3)Hexagonal Close-Packed Structure(hep) Key points:Understand the meaning of Close-Packed Structures'.Be familiar with the difference between hep and fec structures (4)Diamond Structure Key points:Be familiar with the Diamond Structure.Know how to figure out the corresponding lattice structure,primitive cells,basis,and lattice type. (5)CubicZinc Sulfide Structure Key points:Be familiar with the Cubic Zinc Sulfide Structure.Know how to figure out the corresponding lattice structure,primitive cells,basis,and lattice type. 4.Teaching method self-directed 5.Evaluation Via homework assignments,thinking questions in class,quizzes Chapter 2 Wave Diffraction and the Reciprocal Lattice 1.Teaching Aim In this chapter students study the wave diffraction of crystal lattice and the concept of reciprocal attice.to be familiar with the experiments of -ray diffraction by crystals.Master the Bragg Law and Equationas well as LaueEquationo Formulation Understand the equivalence of Bragg's and Laue's views of the X-ray diffraction in crystals. Understand the reason and the background for the introduction of reciprocal lattice.Master the relations between the direct and the reciprocal lattices. 2.Difficult Points Establish aclear and full picture of crystal structure,crystal (direct)lattice,and reciprocal lattice
Section 4. Simple Crystal Structures (1) Sodium Chloride Structure Key points: Be familiar with the Sodium Chloride Structure. Know how to figure out the corresponding lattice structure, primitive cells, basis, and lattice type. (2) Cesium Chloride Structure Key points: Be familiar with the Cesium Chloride Structure. Know how to figure out the corresponding lattice structure, primitive cells, basis, and lattice type. (3) Hexagonal Close-Packed Structure (hcp) Key points: Understand the meaning of ‘Close-Packed Structures’. Be familiar with the difference between hcp and fcc structures. (4) Diamond Structure Key points: Be familiar with the Diamond Structure. Know how to figure out the corresponding lattice structure, primitive cells, basis, and lattice type. (5) Cubic Zinc Sulfide Structure Key points: Be familiar with the Cubic Zinc Sulfide Structure. Know how to figure out the corresponding lattice structure, primitive cells, basis, and lattice type. 4. Teaching method PPT lectures, Handwritten derivation in class, discussion in class, tutorial after class, self-directed learning. 5. Evaluation Via homework assignments, thinking questions in class, quizzes. Chapter 2 Wave Diffraction and the Reciprocal Lattice 1. Teaching Aim In this chapter students study the wave diffraction of crystal lattice and the concept of reciprocal lattice. Students are required to be familiar with the experiments of X-ray diffraction by crystals. Master the Bragg Law and Equation as well as Laue Equation or Formulation. Understand the equivalence of Bragg’s and Laue’s views of the X-ray diffraction in crystals. Understand the reason and the background for the introduction of reciprocal lattice. Master the relations between the direct and the reciprocal lattices. 2. Difficult Points Establish a clear and full picture of crystal structure, crystal (direct) lattice, and reciprocal lattice

3.Teaching Contents Section 1.Diffraction of Waves by Crystals (1)Bragg Law Key points:Understand why the crystal planes can be treated as mirrors with specular reflection.Beable to derive the Braggqionidering two neighbor crystal planes. Section 2.Scattered Wave Amplitude (1)Fourier Analysis Key points:Understand the Fourier components of physical properties in crystals. (2)Reciprocal Lattice Vectors Key points:Master the method to obtain reciprocal lattice vectors (3)Diffraction Conditions Key points:Understand the diffraction conditions of an incident wave in crystals. (4)④Laue Equations Key points:Be able to derive the Laue Equations and understand their equivalence to the Bragg Law. Section 3.Brillouin Zones Key points:Be familiar with the reciprocal lattices to the se.bec.and fec lattices.Grasp the method to find the Brillouin Zones of reciprocal lattice. 4.Teaching method PPT lectures.Handwritten derivation in class.discussion in class tutorial after class sef-directedeain 5.Evaluation Via homework assignments,thinking questions in class,quizzes. Chapter 3 Crystal Binding and Elastic Constants 1.Teaching Aim In this chapter students study the interatomic coupling for different elements.The energetic. mechanical,and geometric properties are discussed for typical binding types of atoms to construct crystal structures.Students are required to be familiar with the concept of binding constants for some simple cases
3. Teaching Contents Section 1. Diffraction of Waves by Crystals (1) Bragg Law Key points: Understand why the crystal planes can be treated as mirrors with specular reflection. Be able to derive the Bragg equation considering two neighbor crystal planes. Section 2. Scattered Wave Amplitude (1) Fourier Analysis Key points: Understand the Fourier components of physical properties in crystals. (2) Reciprocal Lattice Vectors Key points: Master the method to obtain reciprocal lattice vectors. (3) Diffraction Conditions Key points: Understand the diffraction conditions of an incident wave in crystals. (4) Laue Equations Key points: Be able to derive the Laue Equations and understand their equivalence to the Bragg Law. Section 3. Brillouin Zones Key points: Be familiar with the reciprocal lattices to the sc, bcc, and fcc lattices. Grasp the method to find the Brillouin Zones of reciprocal lattice. 4. Teaching method PPT lectures, Handwritten derivation in class, discussion in class, tutorial after class, self-directed learning. 5. Evaluation Via homework assignments, thinking questions in class, quizzes. Chapter 3 Crystal Binding and Elastic Constants 1. Teaching Aim In this chapter students study the interatomic coupling for different elements. The energetic, mechanical, and geometric properties are discussed for typical binding types of atoms to construct crystal structures. Students are required to be familiar with the concept of binding energy and be able to estimate the binding energy, equilibrium lattice constant, and elastic constants for some simple cases

2.Difficult Points Estimate the energy versus the latice constant of crystal from the interatomic coupling for an atom pair. 3.Teaching Contents Section 1.Crystals of Inert Gases (1)Van der Waals-London Interaction Key points:Understand the physical mechanism of Van der Waals-London Interaction and be familiar with the simple model for the interaction. (2)Repulsive Interaction Key points:Understand theoriginsof the interatomic repusive interaction (3)Equilibrium Lattice Constants Key points:Estimate the equilibrium lattice constants for a known crystal structure from the interatomic coupling. (4)Cohesive(Binding)energy Key points:Be familiar with the definition of Binding energy and be able to apply it for analysis of crystal stability. Section 2.Ionic Crystals (1)Electrostatic or Madelung Energy Key points:Understand the importance of direct Coulomb interaction in ionic crystals (2)Evaluation of the Madelung Constant Key points:Be familiar with the calculation of Madelung constant for simple crystals Section 3.Covalent Crystals Key points:Be familiar with the features of covalent crystals. Section 4.Metals Key points:Be familiar with the features of metallic erystals. Section 5.Hydrogen Bonds Key points:Be able to identify hydrogen bonds and typical materials with hydrogen bonds 4.Teaching method PPTlectures,handwritten derivation,discussion,tutorial afer self-directed leaming. 5.Evaluation Via homework assignments,thinking questions in class,quizzes
2. Difficult Points Estimate the energy versus the lattice constant of crystal from the interatomic coupling for an atom pair. 3. Teaching Contents Section 1. Crystals of Inert Gases (1) Van der Waals-London Interaction Key points: Understand the physical mechanism of Van der Waals-London Interaction and be familiar with the simple model for the interaction. (2) Repulsive Interaction Key points: Understand the origins of the interatomic repulsive interaction. (3) Equilibrium Lattice Constants Key points: Estimate the equilibrium lattice constants for a known crystal structure from the interatomic coupling. (4) Cohesive (Binding) energy Key points: Be familiar with the definition of Binding energy and be able to apply it for analysis of crystal stability. Section 2. Ionic Crystals (1) Electrostatic or Madelung Energy Key points: Understand the importance of direct Coulomb interaction in ionic crystals. (2) Evaluation of the Madelung Constant Key points: Be familiar with the calculation of Madelung constant for simple crystals. Section 3. Covalent Crystals Key points: Be familiar with the features of covalent crystals. Section 4. Metals Key points: Be familiar with the features of metallic crystals. Section 5. Hydrogen Bonds Key points: Be able to identify hydrogen bonds and typical materials with hydrogen bonds. 4. Teaching method PPT lectures, handwritten derivation, discussion, tutorial after class, self-directed learning. 5. Evaluation Via homework assignments, thinking questions in class, quizzes

Chapter 4 Phonon I.Crystal Vibrations 1.Teaching Aim In this chapter students study the dynamics of atoms in crystals and derive vibration modes of atoms in simple cases students are required to understand the physical origin of the adiabatic ion,be able toex act the Hook constant from the crystals.Students should also establish the connection between the degree of freedom and the mode number and understand the reason why only the modes are distributed in the first Brillouin zone. 2.Difficult Points Switch between real space and k-space when discussing atomic dynamics in crystals. Distinguish the group velocity from the phase velocity. 3.Teaching Contents Section 1.Vibrations of Crystals with Monatomic Basis (1)First Brillouin Zone Key points:Establish the dynamic equation of atoms connected via spring to neighbors in the one-dimensional monatomic crystal chain,and derive the vibration modes in the first Brillouin zone. (2)Group Velocity Key points:Figure out the dispersion relation of vibration modes and derive the group velocity of each mode. (3)Long Wavelength Limit Key points:In the long wavelength limit estimate the sound velocity and compare it with the result of elastic wave. Section 2.Two Atoms per Primitive Basis Key points:Derive the phonon dispersion for one-dimensional diatomic chain Section 3.Quantization of Elastic Waves Key points:Phonon is quasi-particle due to the quantization of vibration wave. Section 4.Phonon Momentum Key points:Understand the phonon momentum and know how to use it 4.Teaching method PPTlectures,Handwritten derivation in class,discussion in class,tutorial after class
Chapter 4 Phonon I. Crystal Vibrations 1. Teaching Aim In this chapter students study the dynamics of atoms in crystals and derive vibration modes of atoms in simple cases. Students are required to understand the physical origin of the adiabatic approximation and the harmonic approximation, be able to extract the Hook constant from the interatomic coupling, and be familiar with the derivation of vibration modes in one-dimensional crystals. Students should also establish the connection between the degree of freedom and the mode number and understand the reason why only the modes are distributed in the first Brillouin zone. 2. Difficult Points Switch between real space and k-space when discussing atomic dynamics in crystals. Distinguish the group velocity from the phase velocity. 3. Teaching Contents Section 1. Vibrations of Crystals with Monatomic Basis (1) First Brillouin Zone Key points: Establish the dynamic equation of atoms connected via spring to neighbors in the one-dimensional monatomic crystal chain, and derive the vibration modes in the first Brillouin zone. (2) Group Velocity Key points: Figure out the dispersion relation of vibration modes and derive the group velocity of each mode. (3) Long Wavelength Limit Key points: In the long wavelength limit estimate the sound velocity and compare it with the result of elastic wave. Section 2. Two Atoms per Primitive Basis Key points: Derive the phonon dispersion for one-dimensional diatomic chain. Section 3. Quantization of Elastic Waves Key points: Phonon is quasi-particle due to the quantization of vibration wave. Section 4. Phonon Momentum Key points: Understand the phonon momentum and know how to use it. 4. Teaching method PPT lectures, Handwritten derivation in class, discussion in class, tutorial after class, self-directed learning

5.Evaluation Via homework assignments,thinking questions in class.quizzes Chapter 5 Phonon II.Thermal Properties 1.Teaching Aim In this hapter students study the density of states and the thermal Students are required to derive the heat capacities of phonons in the Einstein and the Debye models.Comparing the results with those obtained in classical gases.students should understand the quantum effects on thermal properties and the result of zero point energy. 2.Difficult Points Understand the density of states and use itin the calculation of thermal properties.Obtain th total energy by integrating the energies of phonons and derive the limit at low and high temperatures. 3.Teaching Contents Section 1.Phonon Heat capacity (1)Bose-Einstein(Plank)Distribution Key points:Be familiar with the Bose-Einstein(Plank)Distribution for phonons. (2)Normal Mode Enumeration Key points:Transfer the summation over states into integration with the density of states (3)Density of States in One Dimension Key points:Density of states in energy space can be derived from the constant density of states in k-space.Theyare the group velocity which can be obtained from the dispersion. (4)Density of States in Three Dimension Key points:Similarly.density of states in three dimension is obtained from the constant density of states in k-space and dispersion. (5)Debye Model for Density of States Key points:Density of states in obtained by assuming linear dispersion or constant sound velocity. Key points:Heat capacity is proportionl to cubic power of temperature in the Debye model (7)Einstein Model of the Density of States
5. Evaluation Via homework assignments, thinking questions in class, quizzes. Chapter 5 Phonon II. Thermal Properties 1. Teaching Aim In this chapter students study the density of states and the thermal properties of phonons. Students are required to derive the heat capacities of phonons in the Einstein and the Debye models. Comparing the results with those obtained in classical gases, students should understand the quantum effects on thermal properties and the result of zero point energy. 2. Difficult Points Understand the density of states and use it in the calculation of thermal properties. Obtain the total energy by integrating the energies of phonons and derive the limit at low and high temperatures. 3. Teaching Contents Section 1. Phonon Heat capacity (1) Bose-Einstein (Plank) Distribution Key points: Be familiar with the Bose-Einstein (Plank) Distribution for phonons. (2) Normal Mode Enumeration Key points: Transfer the summation over states into integration with the density of states. (3) Density of States in One Dimension Key points: Density of states in energy space can be derived from the constant density of states in k-space. They are connected by the group velocity which can be obtained from the dispersion. (4) Density of States in Three Dimension Key points: Similarly, density of states in three dimension is obtained from the constant density of states in k-space and dispersion. (5) Debye Model for Density of States Key points: Density of states in obtained by assuming linear dispersion or constant sound velocity. (6) Debye T3 Law Key points: Heat capacity is proportional to cubic power of temperature in the Debye model. (7) Einstein Model of the Density of States

Key points:Density of states in obtained by assuming constant energy/frequency of phonon. The Heat capacity decreases exponentially at low temperature in the Ein odel 4.Teaching method PPT lectures.Handwritten derivation in class.discussion in class.tutorial after class. self-directed learning. 5.Evaluation Via homework assignments,thinking questions in class,quizzes. Chapter 6 Free Electron Fermi Gas 1.Teaching Aim In this chapter students study the quantum description of free electrons with Coulomb interaction between electrons neglected.Students are required to derive the Fermi energy and understand the temperature dependence of the Fermi energy in systems of different dimensions Thermal properties of Fermi gas are discussed. 2.Difficult Points Connect the thermal&electric properties with the system parameters such as electron mass. density of states,density ofelectrons,dimensionality,and temperature,etc. 3.Teaching Contents Section 1.Energy Levels in One dimension Key points:Solve the Schrodinger equation to obtain the energy levels of standing electrons in one-dimensional square well.Energy levels of propagating electrons can be obtained using the periodic boundary condition. Section 2.Effect of Temperature on the Fermi-Dirac Distribution Key points:Be familiar with the variation of Fermi-Dirac distribution at different temperature. Section 3.Free Electron Gas in Three Dimensions Key points:Extend the one-dimensional results to three-dimensional cases.Notice the k-space difference between the standing and the propagating states and the difference in density of states between three-and one-dimensional systems. Section 4.Heat Capacity of the Electron Gas Key points:Calculate the energy of electron gas versus temperature with the temperature dependence of Fermi-Dirac distribution. Section 5.Electrical Conductivity and Ohm's Law
Key points: Density of states in obtained by assuming constant energy/frequency of phonon. The Heat capacity decreases exponentially at low temperature in the Einstein model. 4. Teaching method PPT lectures, Handwritten derivation in class, discussion in class, tutorial after class, self-directed learning. 5. Evaluation Via homework assignments, thinking questions in class, quizzes. Chapter 6 Free Electron Fermi Gas 1. Teaching Aim In this chapter students study the quantum description of free electrons with Coulomb interaction between electrons neglected. Students are required to derive the Fermi energy and understand the temperature dependence of the Fermi energy in systems of different dimensions. Thermal and electric properties of free electron Fermi gas are discussed. 2. Difficult Points Connect the thermal & electric properties with the system parameters such as electron mass, density of states, density of electrons, dimensionality, and temperature, etc. 3. Teaching Contents Section 1. Energy Levels in One dimension Key points: Solve the Schrodinger equation to obtain the energy levels of standing electrons in one-dimensional square well. Energy levels of propagating electrons can be obtained using the periodic boundary condition. Section 2. Effect of Temperature on the Fermi-Dirac Distribution Key points: Be familiar with the variation of Fermi-Dirac distribution at different temperature. Section 3. Free Electron Gas in Three Dimensions Key points: Extend the one-dimensional results to three-dimensional cases. Notice the k-space difference between the standing and the propagating states and the difference in density of states between three- and one-dimensional systems. Section 4. Heat Capacity of the Electron Gas Key points: Calculate the energy of electron gas versus temperature with the temperature dependence of Fermi-Dirac distribution. Section 5. Electrical Conductivity and Ohm’s Law

Key points:With the collision time known,electrical conductivity can be derived by estimating the momentum deviationunder an i field. Section 6.Thermal Conduetivity of Metals Key points:Thermal conductivity can be estimated by assuming a temperature gradient 4.Teaching method self-directed learning. 5.Evaluation Via homework assignments,thinking questions in class,quizzes. Chapter 7 Energy Bands 1.Teaching Aim In this chapter students study the energy bands-the electronic structure of electron gas in and the Bloch functions bands. 2.Difficult Points Prove and understand the Bloch theorem.Be familiar with the features of Bloch functions 3.Teaching Contents Section 1.Nearly Free Electron Model (1)Origin of the Energy Gap Key points:Understand the origin of the energy gap by considering redistribution of electrons in periodic potential. (2)Magnitude of the Energy Gap Key points:Estimate the energy difference of two standing waves in a periodic potential. Section 2.Bloch Functions Key points:Be familiar with the form of Bloch functions. Section 3.Kronig-Penney Model Key points:In the Kronig-Penney Model the energy bands can be solved exactly from the Schrodinger equation.This convinces us the existence of energy bands Section 4.Wave Equation of Electron in a Periodic Potential (1)Restatement of the Bloch Theorem
Key points: With the collision time known, electrical conductivity can be derived by estimating the momentum deviation under an electric field. Section 6. Thermal Conductivity of Metals Key points: Thermal conductivity can be estimated by assuming a temperature gradient. 4. Teaching method PPT lectures, Handwritten derivation in class, discussion in class, tutorial after class, self-directed learning. 5. Evaluation Via homework assignments, thinking questions in class, quizzes. Chapter 7 Energy Bands 1. Teaching Aim In this chapter students study the energy bands – the electronic structure of electron gas in periodic potential. Students should be familiar with the Bloch theorem and the Bloch functions. Students are required to understand well the physical mechanism behind the formation of energy bands. 2. Difficult Points Prove and understand the Bloch theorem. Be familiar with the features of Bloch functions. 3. Teaching Contents Section 1. Nearly Free Electron Model (1) Origin of the Energy Gap Key points: Understand the origin of the energy gap by considering redistribution of electrons in periodic potential. (2) Magnitude of the Energy Gap Key points: Estimate the energy difference of two standing waves in a periodic potential. Section 2. Bloch Functions Key points: Be familiar with the form of Bloch functions. Section 3. Kronig-Penney Model Key points: In the Kronig-Penney Model the energy bands can be solved exactly from the Schrodinger equation. This convinces us the existence of energy bands.. Section 4. Wave Equation of Electron in a Periodic Potential (1) Restatement of the Bloch Theorem