
《数学物理方法》课程教学大纲 一、课程基本信息 英文名称Mathematical Methods for Physics 课程代码 PHYS2002 课程性质大类基础课程 授课对象 物理学 学分4学分 学时 72学时 主讲教师 徐震宇 修订日期 2021年9月 指定教材 四川大学数学学院高等数学、微分方程教研室编,高等数学第四册(第三版),北 京:高等教有出版社,2010年 二、课程目标 (一)总体目标: 本课程的总体目标是使学生在高等数学和普通物理学的基础上学习复变函数和数学物 理方程的基础知识,并了解近年来相关理论的新进展,为后继物理学专业课程学习和科研 作中将要遇到的相关数学物理问题打下基础。与此同时培养和锻炼学生的科学思维能力、科 学创新能力和解决实际数理问题的能力:掌握辩证唯物主义基本原理,建立科学的世界观和 方法论,使学生富有科学精神,勇于探索未知的研究领域。 (二)课程目标: 课程目标1:了解复变函数理论建立和发展的历史:掌握解析函数的定义和常见初等解 析函数的性质及计算方法:掌握柯西积分定理和柯西积分公式:掌握解析函数的幂级数表示 和洛朗级数的展开:掌握留数的计算方法。掌握辩证唯物主义基本原理,建立科学的世界观 和方法论。 课程目标2:掌握利用留数计算实积分的方法:了解复变函数中的共形映射:了解解析 延拓及Γ函数、黎曼(函数。训练学生运用所学复变函数理论求解实际物理问题中遇到的各 类复杂积分的能力,培养和提高学生的抽象思维能力和科研创新能力。 课程目标3:掌握一维波动方程的建立和傅里叶求解方法:掌握热传导方程的傅里叶解 法:掌握二维拉普拉斯方程的傅里叶解法:了解波动方程的达朗贝尔解法:掌握傅里叶变换 掌提几类常见的特殊函数,如勒让德多项式和贝塞尔函数等。培养学生对常见数理方程和特 殊多项式的求解计算能力。 课程目标4:了解施图姆-刘维尔本征问题。体会数理方程建立过程中的物理思想方法, 培养学生模型建构、分析与综合、推理类比等科学思维方法,培养学生的爱国热情,探索未 知、追求真理、永攀高峰的责任感和使命感
1 《数学物理方法》课程教学大纲 一、课程基本信息 英文名称 Mathematical Methods for Physics 课程代码 PHYS2002 课程性质 大类基础课程 授课对象 物理学 学 分 4 学分 学 时 72 学时 主讲教师 徐震宇 修订日期 2021 年 9 月 指定教材 四川大学数学学院高等数学、微分方程教研室编,高等数学第四册(第三版), 北 京:高等教育出版社,2010 年 二、课程目标 (一)总体目标: 本课程的总体目标是使学生在高等数学和普通物理学的基础上学习复变函数和数学物 理方程的基础知识,并了解近年来相关理论的新进展,为后继物理学专业课程学习和科研工 作中将要遇到的相关数学物理问题打下基础。与此同时培养和锻炼学生的科学思维能力、科 学创新能力和解决实际数理问题的能力;掌握辩证唯物主义基本原理,建立科学的世界观和 方法论,使学生富有科学精神,勇于探索未知的研究领域。 (二)课程目标: 课程目标 1:了解复变函数理论建立和发展的历史;掌握解析函数的定义和常见初等解 析函数的性质及计算方法;掌握柯西积分定理和柯西积分公式;掌握解析函数的幂级数表示 和洛朗级数的展开;掌握留数的计算方法。掌握辩证唯物主义基本原理,建立科学的世界观 和方法论。 课程目标 2:掌握利用留数计算实积分的方法;了解复变函数中的共形映射;了解解析 延拓及Γ函数、黎曼ζ函数。训练学生运用所学复变函数理论求解实际物理问题中遇到的各 类复杂积分的能力,培养和提高学生的抽象思维能力和科研创新能力。 课程目标 3:掌握一维波动方程的建立和傅里叶求解方法;掌握热传导方程的傅里叶解 法;掌握二维拉普拉斯方程的傅里叶解法;了解波动方程的达朗贝尔解法;掌握傅里叶变换; 掌握几类常见的特殊函数,如勒让德多项式和贝塞尔函数等。培养学生对常见数理方程和特 殊多项式的求解计算能力。 课程目标 4:了解施图姆-刘维尔本征问题。体会数理方程建立过程中的物理思想方法, 培养学生模型建构、分析与综合、推理类比等科学思维方法,培养学生的爱国热情,探索未 知、追求真理、永攀高峰的责任感和使命感
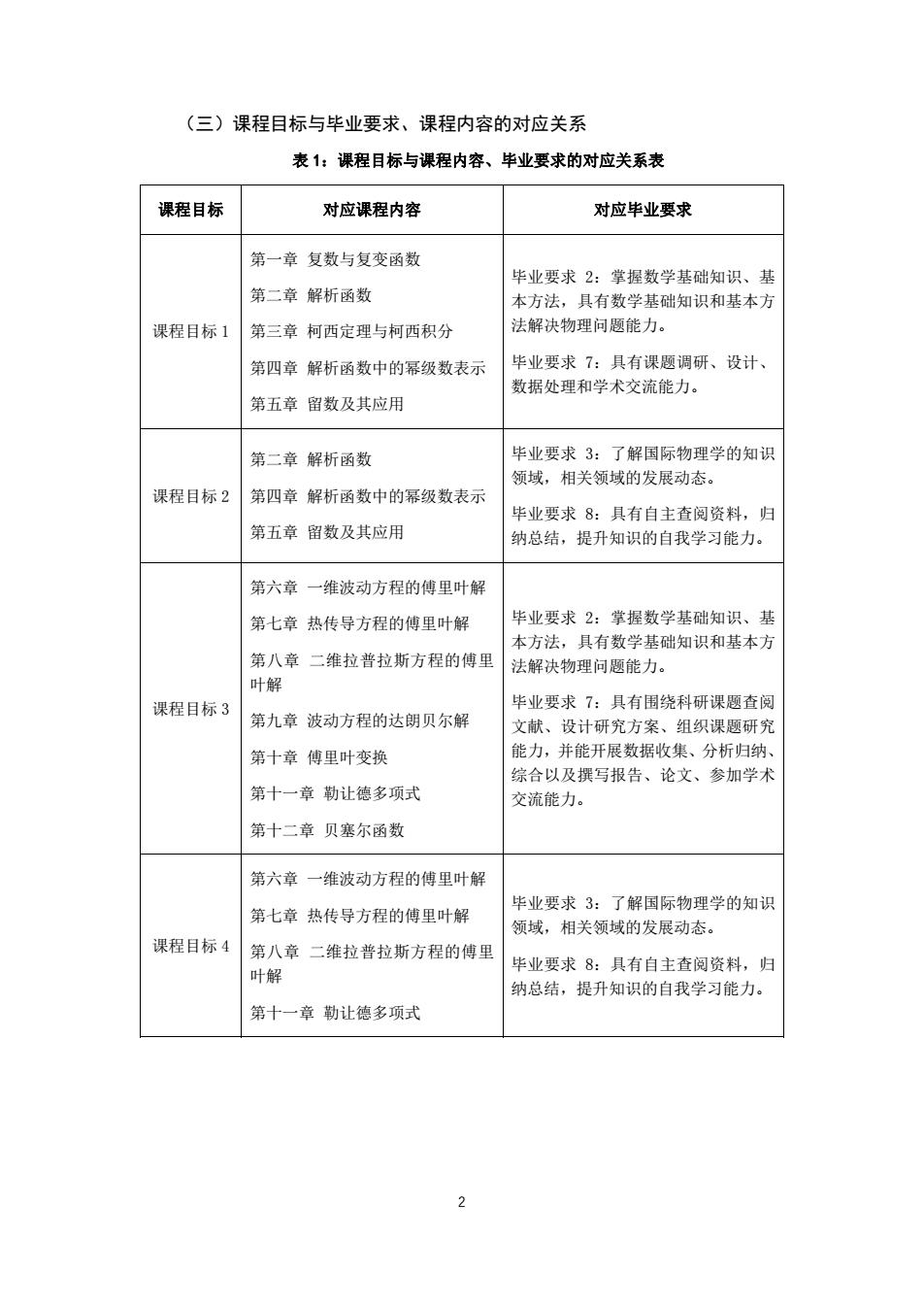
(三)课程目标与毕业要求、课程内容的对应关系 表1:课程目标与课程内容、毕业要求的对应关系表 课程目标 对应课程内容 对应毕业要求 第一章复数与复变函数 毕业要求2:掌握数学基础知识、基 第二章解析函数 本方法,具有数学基础知识和基本方 课程目标1 第三章柯西定理与柯西积分 法解决物理问题能力。 第四章解析函数中的幂级数表示 毕业要求7:具有课题调研、设计 数据处理和学术交流能力。 第五章留数及其应用 第二章解析函数 毕业要求3:了解国际物理学的知识 领域,相关领域的发展动态。 课程目标2 第四章解析函数中的幂级数表示 毕业要求8:具有自主查阅资料,归 第五章留数及其应用 纳总结,提升知识的自我学习能力。 第六章一维波动方程的傅里叶解 第七章热传导方程的傅里叶解 毕业要求2:掌握数学基础知识、基 本方法,具有数学基础知识和基本方 第八章二维拉普拉斯方程的傅里 法解决物理问题能力。 叶解 课程目标3 毕业要求7:具有围绕科研课题查阅 第九章波动方程的达朗贝尔解 文献、设计研究方蜜、组织课颗研劳 第十章傅里叶变换 能力,并能 开展数据收集、分析归邹 综合以及撰写报告、论文、参加学术 第十一章勒让德多项式 交流能力。 第十二章贝塞尔函数 第六章一维波动方程的傅里叶解 第七章热传导方程的傅里叶解 毕业要求3:了解国际物理学的知识 领域,相关领域的发展动态。 课程目标4 第八章二维拉普拉斯方程的傅里 叶解 毕业要求8:具有自主查阅资料,归 纳总结,提升知识的自我学习能力。 第十一章勒让德多项式
2 (三)课程目标与毕业要求、课程内容的对应关系 表 1:课程目标与课程内容、毕业要求的对应关系表 课程目标 对应课程内容 对应毕业要求 课程目标 1 第一章 复数与复变函数 第二章 解析函数 第三章 柯西定理与柯西积分 第四章 解析函数中的幂级数表示 第五章 留数及其应用 毕业要求 2:掌握数学基础知识、基 本方法,具有数学基础知识和基本方 法解决物理问题能力。 毕业要求 7:具有课题调研、设计、 数据处理和学术交流能力。 课程目标 2 第二章 解析函数 第四章 解析函数中的幂级数表示 第五章 留数及其应用 毕业要求 3:了解国际物理学的知识 领域,相关领域的发展动态。 毕业要求 8:具有自主查阅资料,归 纳总结,提升知识的自我学习能力。 课程目标 3 第六章 一维波动方程的傅里叶解 第七章 热传导方程的傅里叶解 第八章 二维拉普拉斯方程的傅里 叶解 第九章 波动方程的达朗贝尔解 第十章 傅里叶变换 第十一章 勒让德多项式 第十二章 贝塞尔函数 毕业要求 2:掌握数学基础知识、基 本方法,具有数学基础知识和基本方 法解决物理问题能力。 毕业要求 7:具有围绕科研课题查阅 文献、设计研究方案、组织课题研究 能力,并能开展数据收集、分析归纳、 综合以及撰写报告、论文、参加学术 交流能力。 课程目标 4 第六章 一维波动方程的傅里叶解 第七章 热传导方程的傅里叶解 第八章 二维拉普拉斯方程的傅里 叶解 第十一章 勒让德多项式 毕业要求 3:了解国际物理学的知识 领域,相关领域的发展动态。 毕业要求 8:具有自主查阅资料,归 纳总结,提升知识的自我学习能力

三、教学内容 第一章复数与复变函数 1.教学目标 复数的运算要熟练,正确理解区域、单连域,多连域,简单曲线等概念。正确理解复变 函数及与之有关的概念。 2.教学重难点 复数、复变函数的基本概念、复球面与无穷远点。 3.教学内容 复数域、复平面、复数的模与幅角、复数的乘幂与方根:区域、复变函数的极限与连续 性:复球面 4.教学方法 教师讲授,师生讨论等等 5.教学评价 课后相应习题、补充习题。 第二章解析函数 1教学目标 正确理解复变函数的导数、解析函数等基本概念:掌握并能运用柯西黎曼条件,要知 道解析函数与调和函数的关系:掌握初等解析函数的定义和主要性质。 2.教学重难点 解析函数的概念及柯西黎曼条件,解析函数与调和函数的关系,初等解析函数。 3.教学内容 复变函数的导数与微分、柯西黎曼条件、解析函数的定义、共形映射:共轭调和函数 的求法、共把调和函数的几何意义:初等单值函数、多值函数。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题
3 三、教学内容 第一章 复数与复变函数 1.教学目标 复数的运算要熟练,正确理解区域、单连域,多连域,简单曲线等概念。正确理解复变 函数及与之有关的概念。 2.教学重难点 复数、复变函数的基本概念、复球面与无穷远点。 3.教学内容 复数域、复平面、复数的模与幅角、复数的乘幂与方根;区域、复变函数的极限与连续 性;复球面。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题。 第二章 解析函数 1. 教学目标 正确理解复变函数的导数、解析函数等基本概念;掌握并能运用柯西-黎曼条件,要知 道解析函数与调和函数的关系;掌握初等解析函数的定义和主要性质。 2. 教学重难点 解析函数的概念及柯西-黎曼条件,解析函数与调和函数的关系,初等解析函数。 3. 教学内容 复变函数的导数与微分、柯西-黎曼条件、解析函数的定义、共形映射;共轭调和函数 的求法、共轭调和函数的几何意义;初等单值函数、多值函数。 4. 教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题

第三章柯西定理与柯西积分 1.教学目标 正确理解复变函数积分的概念,掌握复变函数积分的一般计算法,掌握并能运用柯西 积分定理,复合闭路定理和柯西积分公式,高阶导数公式,特别要能运用它们来计算积分 2.教学重点难点 复变函数积分的概念及其简单性质,柯西积分定理及其推广,柯西积分公式及其推广。 3.教学内容 复变函数积分的定义及其计算方法、复变函数积分的简单性质:柯西积分定理、不定 积分、复围线情况:柯西积分公式、解析函数的无限次可微性、莫雷拉定理等。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题 第四章解析函数的幂级数表示 1.教学目标 正确理解级数收敛、发散与绝对收敛等概念:要求会把比较简单的解析函数展开成泰 勒级数并指出其收敛半径:要求会把较简单的函数展开成洛朗级数:正确理解孤立奇点的概 念及其分类:了解解析延拓及『函数、黎曼(函数。 2.教学重点难点 函数项级数的基本性质,幂级数与解析函数,洛朗级数,单值函数的孤立奇点, 3.教学内容 数项级数、一致收敛的函数项级数:幂级数的收敛性、解析函数的幂级数表示、解析 函数零点的孤立性及唯一性定理:洛朗级数的收敛圆环、解析函数的洛朗展开:孤立奇点的 类型及判断:解析延拓及函数、黎曼5函数。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题
4 第三章 柯西定理与柯西积分 1.教学目标 正确理解复变函数积分的概念,掌握复变函数积分的一般计算法,掌握并能运用柯西 积分定理,复合闭路定理和柯西积分公式,高阶导数公式,特别要能运用它们来计算积分。 2. 教学重点难点 复变函数积分的概念及其简单性质,柯西积分定理及其推广,柯西积分公式及其推广。 3.教学内容 复变函数积分的定义及其计算方法、复变函数积分的简单性质;柯西积分定理、不定 积分、复围线情况;柯西积分公式、解析函数的无限次可微性、莫雷拉定理等。 4. 教学方法 教师讲授,师生讨论等等。 5. 教学评价 课后相应习题、补充习题 第四章 解析函数的幂级数表示 1.教学目标 正确理解级数收敛、发散与绝对收敛等概念;要求会把比较简单的解析函数展开成泰 勒级数并指出其收敛半径;要求会把较简单的函数展开成洛朗级数;正确理解孤立奇点的概 念及其分类;了解解析延拓及Γ函数、黎曼ζ函数。 2.教学重点难点 函数项级数的基本性质,幂级数与解析函数,洛朗级数,单值函数的孤立奇点。 3.教学内容 数项级数、一致收敛的函数项级数;幂级数的收敛性、解析函数的幂级数表示、解析 函数零点的孤立性及唯一性定理;洛朗级数的收敛圆环、解析函数的洛朗展开;孤立奇点的 类型及判断;解析延拓及Γ函数、黎曼ζ函数。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题

第五章留数及其应用 1教学目标 正确理解函数在孤立奇点的留数概念,掌握并能应用留数定理,掌握留数的计算方法 并能利用留数计算某些实积分 2.教学重点难点 留数、利用留数计算实积分。 3.教学内容 留数的定义及留数定理、留数的求法、无穷远点的留数:利用留数计算实积分,包括 各种实例。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题。 第六章一维波动方程的傅里叶解 1.教学目标 学习如何建立弦振动方程及提出方程的定解条件:掌握用分离变量法求解齐次方程混合 问题并了解其解的物理意义:掌握非齐次方程的求解及边界条件齐次化的方法。 2教学重点难点 一维波动方程一弦振动方程的建立:齐次方程混合问题的傅里叶解法分离变量法),强 迫振动、非齐次方程的求解。 3.教学内容 弦振动方程的建立、定解条件的提出:利用分离变量法求解齐次弦振动方程的混合问 题:傅里叶解的物理意义:电报方程:非齐次方程的求解。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题。 5
5 第五章 留数及其应用 1.教学目标 正确理解函数在孤立奇点的留数概念,掌握并能应用留数定理,掌握留数的计算方法, 并能利用留数计算某些实积分。 2.教学重点难点 留数、利用留数计算实积分。 3.教学内容 留数的定义及留数定理、留数的求法、无穷远点的留数;利用留数计算实积分,包括 各种实例。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题。 第六章 一维波动方程的傅里叶解 1.教学目标 学习如何建立弦振动方程及提出方程的定解条件;掌握用分离变量法求解齐次方程混合 问题并了解其解的物理意义;掌握非齐次方程的求解及边界条件齐次化的方法。 2.教学重点难点 一维波动方程--弦振动方程的建立;齐次方程混合问题的傅里叶解法(分离变量法),强 迫振动、非齐次方程的求解。 3.教学内容 弦振动方程的建立、定解条件的提出;利用分离变量法求解齐次弦振动方程的混合问 题;傅里叶解的物理意义;电报方程;非齐次方程的求解。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题

第七章热传导方程的傅里叶解 1教学目标 学习如何建立热传导方程:掌握热传导方程混合间题的傅里叶解法:了解其解的物理意 义。 2.教学重点难点 热传导方程的建立,混合问题的傅里叶解法,初值问题的傅里叶解法。 3.教学内容 热传导方程的建立、扩散方程的建立、定解条件的提出:一端有界的热传导问题。 4.教学方法 教师讲授,师生讨论等等, 5.教学评价 课后相应习题、补充习题。 第八章拉普拉斯方程的圆的狄利克雷问题的傅里叶解法 1教学目标 理解圆的狄利克雷问题:掌握该问题的傅里叶解法:正确理解8函数的基本性质。 2.教学重点难点 圆的狄利克雷问题,6函数 3教学内容 圆的狄利克雷问题及解法、8函数 4.教学方法 教师讲授,师生讨论等等 5.教学评价 课后相应习题、补充习题。 第九章波动方程的达朗贝尔解 1.教学目标 掌握弦振动方程初值问题的达朗贝尔解法:理解解的物理意义:理解依赖区间、决定区 域、影响区域等概念
6 第七章 热传导方程的傅里叶解 1.教学目标 学习如何建立热传导方程;掌握热传导方程混合问题的傅里叶解法;了解其解的物理意 义。 2.教学重点难点 热传导方程的建立,混合问题的傅里叶解法,初值问题的傅里叶解法。 3.教学内容 热传导方程的建立、扩散方程的建立、定解条件的提出;一端有界的热传导问题。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题。 第八章 拉普拉斯方程的圆的狄利克雷问题的傅里叶解法 1.教学目标 理解圆的狄利克雷问题;掌握该问题的傅里叶解法;正确理解δ函数的基本性质。 2.教学重点难点 圆的狄利克雷问题,δ函数。 3.教学内容 圆的狄利克雷问题及解法、δ函数。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题。 第九章 波动方程的达朗贝尔解 1.教学目标 掌握弦振动方程初值问题的达朗贝尔解法;理解解的物理意义;理解依赖区间、决定区 域、影响区域等概念

2教学重点难点 弦振动方程初值问题的达朗贝尔解法。 3教学内容 达朗贝尔解的推导、物理意义:半无界弦振动问题:高维波动方程的解法:推迟势的 概念。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题。 第十章傅里叶变换 1.教学目标 正确理解傅里叶变换的定义及其基本性质:掌握用傅里叶变换法求解某些数理方程:知 道基本解的定义及其物理意义 2.教学重点难点 傅里叶变换的定义及其基本性质,用傅里叶变换解数理方程举例、基本解, 3.教学内容 傅里叶变换的定义、基本性质:利用傅里叶变换求解数理方程。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题。 第十一章勒让德多式 1.教学目标 掌握勒让德方程的推导和求解过程:掌握勒让德多项式的定义及各种表达式:理解如何 利用生成函数导出勒让德多项式的递推公式:掌握按勒让德多项式展开及利用勒让德多项式 求解某些数理方程的方法。 2.教学重点难点 勒让德微分方程及勒让德多项式,勒让德多项式的生成函数及其递推公式,按物让德 多项式展开,拉普拉斯方程在球形区域上的狄利克雷问题
7 2.教学重点难点 弦振动方程初值问题的达朗贝尔解法。 3.教学内容 达朗贝尔解的推导、物理意义;半无界弦振动问题;高维波动方程的解法;推迟势的 概念。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题。 第十章 傅里叶变换 1.教学目标 正确理解傅里叶变换的定义及其基本性质;掌握用傅里叶变换法求解某些数理方程;知 道基本解的定义及其物理意义。 2.教学重点难点 傅里叶变换的定义及其基本性质,用傅里叶变换解数理方程举例、基本解。 3.教学内容 傅里叶变换的定义、基本性质;利用傅里叶变换求解数理方程。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题。 第十一章 勒让德多式 1.教学目标 掌握勒让德方程的推导和求解过程;掌握勒让德多项式的定义及各种表达式;理解如何 利用生成函数导出勒让德多项式的递推公式;掌握按勒让德多项式展开及利用勒让德多项式 求解某些数理方程的方法。 2.教学重点难点 勒让德微分方程及勒让德多项式,勒让德多项式的生成函数及其递推公式,按勒让德 多项式展开,拉普拉斯方程在球形区域上的狄利克雷问题

3.教学内容 施图姆-刘维尔本征问题:勒让德微分方程及勒让德多项式、勒让德微分方程的导出: 生成函数的概念:勒让德多项式的递推公式及性质:连带勒让德多项式等。 4.教学方法 教师讲授,师生讨论等等 5.教学评价 课后相应习题、补充习题。 第十二章贝塞尔函数 1.教学目标 了解贝塞尔微分方程如何导出和求解过程,掌握贝塞耳函数的定义及各种表达式,知道 如何利用贝塞尔函数的生成函数导出其递推公式,掌握按贝塞尔函数展开及利用贝塞耳函数 求解某些数理方程的方法。 2.教学重点难点 贝塞尔微分方程及贝塞耳函数,贝塞耳函数的生成函数及其递推公式,按贝塞尔函数 展开,圆膜振动问题的求解。 3.教学内容 贝塞尔微分方程的推导、贝塞尔函数的定义:贝塞尔函数的生成函数、递推公式及性 质:第二、三类贝塞尔函数等。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题
8 3.教学内容 施图姆-刘维尔本征问题;勒让德微分方程及勒让德多项式、勒让德微分方程的导出; 生成函数的概念;勒让德多项式的递推公式及性质;连带勒让德多项式等。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题。 第十二章 贝塞尔函数 1.教学目标 了解贝塞尔微分方程如何导出和求解过程,掌握贝塞耳函数的定义及各种表达式,知道 如何利用贝塞尔函数的生成函数导出其递推公式,掌握按贝塞尔函数展开及利用贝塞耳函数 求解某些数理方程的方法。 2.教学重点难点 贝塞尔微分方程及贝塞耳函数,贝塞耳函数的生成函数及其递推公式,按贝塞尔函数 展开,圆膜振动问题的求解。 3.教学内容 贝塞尔微分方程的推导、贝塞尔函数的定义;贝塞尔函数的生成函数、递推公式及性 质;第二、三类贝塞尔函数等。 4.教学方法 教师讲授,师生讨论等等。 5.教学评价 课后相应习题、补充习题

四、学时分配 表2:各章节的具体内容和学时分配表 章节 章节内容 学时分配 1 复数与复变函数 4学时 2 解析函数 4学时 3 可西定理与柯西积分 6学时 4 解析函数的幂级数表示 8学时 5 留数及其应用 8学时 6 维波动方程的傅里叶解 6学时 热传导方程的傅里叶解 4学时 8 拉普拉斯方程的圆的狄利克雷问题的傅里叶解 4学时 9 波动方程的达朗贝尔解 2学时 10 傅里叶变换 6学时 11 對让德多项式 8学时 12 贝塞尔函数 8学时 五、教学进度 表3:敦学进度表 章节 授课 周次 内容提要 作业及要求 名称 时数 1 第一章 第一章课后习题:1、2、6 复数与复变函数 8、11、14、补充习题 第二章课后习题:5、8、 2 第二章 解析函数 7 10、17、18、20、补充习 题 3 第三章 柯西定理与柯西积分(一) 见下页
9 四、学时分配 表 2:各章节的具体内容和学时分配表 五、教学进度 表 3:教学进度表 周次 章节 名称 内容提要 授课 时数 作业及要求 备 注 1 第一章 复数与复变函数 4 第一章课后习题:1、2、6、 8、11、14、补充习题 2 第二章 解析函数 4 第二章课后习题:5、8、 10、17、18、20、补充习 题 3 第三章 柯西定理与柯西积分(一) 4 见下页 章节 章节内容 学时分配 1 复数与复变函数 4 学时 2 解析函数 4 学时 3 柯西定理与柯西积分 6 学时 4 解析函数的幂级数表示 8 学时 5 留数及其应用 8 学时 6 一维波动方程的傅里叶解 6 学时 7 热传导方程的傅里叶解 4 学时 8 拉普拉斯方程的圆的狄利克雷问题的傅里叶解 4 学时 9 波动方程的达朗贝尔解 2 学时 10 傅里叶变换 6 学时 11 勒让德多项式 8 学时 12 贝塞尔函数 8 学时
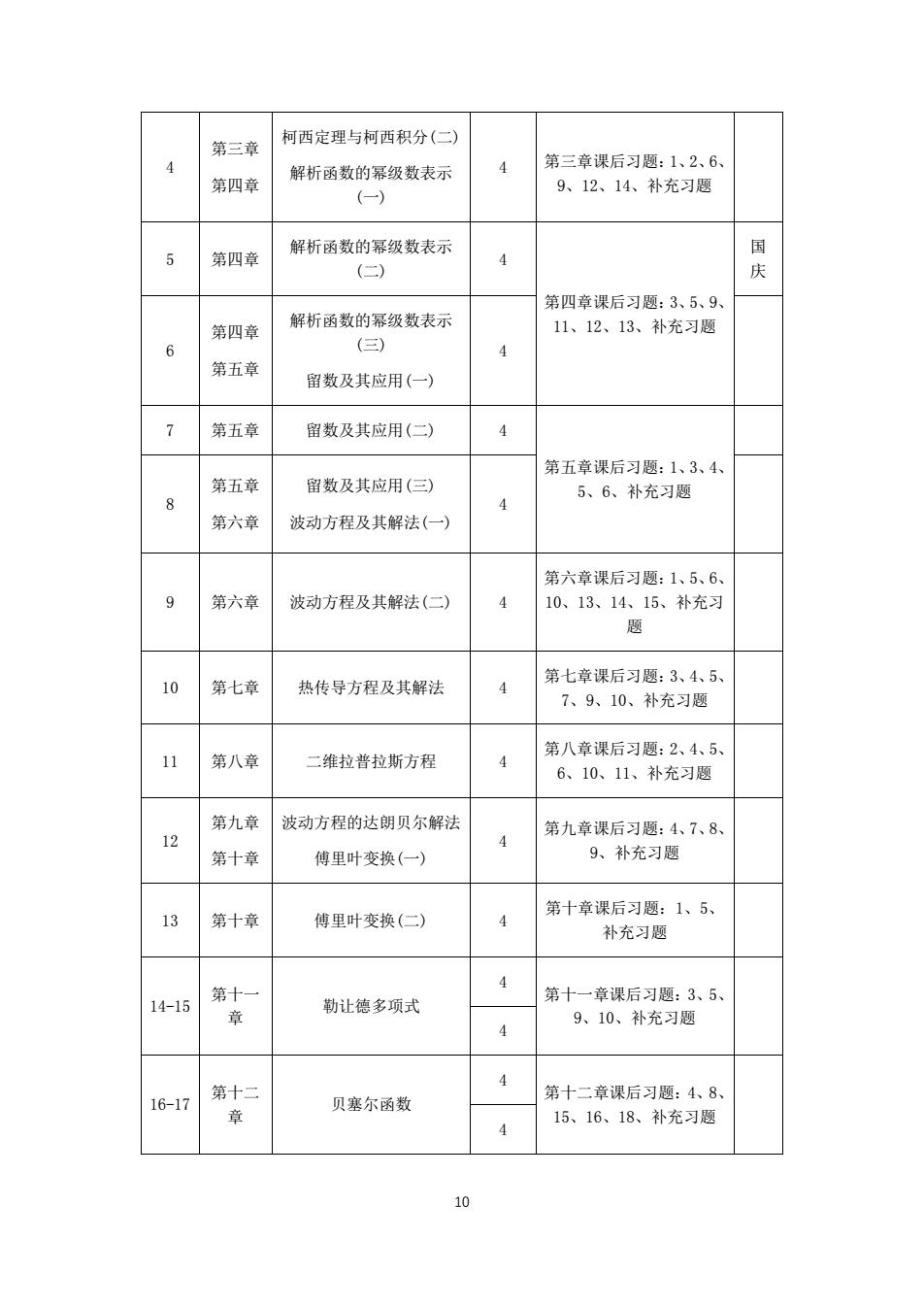
第三章 柯西定理与柯西积分(二) 第二音课后习题.1、26 第四 解析函数的幂级数表示 9、12、14、补充习题 5 第四章 解析函数的幂级数表示 (二) 4 第四章课后习题:3、5、9 第四章 解析函数的幂级数表示 11、12、13、补充习题 6 (三) 4 第五章 留数及其应用(一) 7 第五章 留数及其应用(二) 第五章课后习题:1、3、4 第五章 留数及其应用() 5、6、补充习题 8 第六章 波动方程及其解法(一) 第六章课后习题:1、5、6 9 第六章 波动方程及其解法(二) 4 10、13、14、15、补充习 题 第七章 热传导方程及其解法 第七章课后习题:3、4、5 10 7、9、10、补充习题 第八音课后习题.2、4、5 11 第八章 维拉普拉斯方程 4 6、10、11、补充习题 第九章 波动方程的达朗贝尔解法 12 4 第九章课后习题:4、7、8 第十章 傅里叶变换(一) 9、补充习题 13第十章 傅里叶变换(二) 第十章课后习题:1、5 补充习题 14-15 第十 勒让德多项式 第十一章课后习题:3、5 9、10、补充习题 16-17 第+ 贝塞尔函数 第十二章课后习题:4、8、 15、16、18、补充习慰
10 4 第三章 第四章 柯西定理与柯西积分(二) 解析函数的幂级数表示 (一) 4 第三章课后习题:1、2、6、 9、12、14、补充习题 5 第四章 解析函数的幂级数表示 (二) 4 第四章课后习题:3、5、9、 11、12、13、补充习题 国 庆 6 第四章 第五章 解析函数的幂级数表示 (三) 留数及其应用(一) 4 7 第五章 留数及其应用(二) 4 第五章课后习题:1、3、4、 5、6、补充习题 8 第五章 第六章 留数及其应用(三) 波动方程及其解法(一) 4 9 第六章 波动方程及其解法(二) 4 第六章课后习题:1、5、6、 10、13、14、15、补充习 题 10 第七章 热传导方程及其解法 4 第七章课后习题:3、4、5、 7、9、10、补充习题 11 第八章 二维拉普拉斯方程 4 第八章课后习题:2、4、5、 6、10、11、补充习题 12 第九章 第十章 波动方程的达朗贝尔解法 傅里叶变换(一) 4 第九章课后习题:4、7、8、 9、补充习题 13 第十章 傅里叶变换(二) 4 第十章课后习题:1、5、 补充习题 14-15 第十一 章 勒让德多项式 4 第十一章课后习题:3、5、 9、10、补充习题 4 16-17 第十二 章 贝塞尔函数 4 第十二章课后习题:4、8、 15、16、18、补充习题 4